城市隧道出口与平面交叉合理间距研究

武生权，龙贵云，段绪斌

（1.天津市政工程设计研究总院有限公司，天津300392）

（2.中国水利水电第四工程局有限公司，青海 西宁，810007）

随着我国城市基础设施建设的飞速发展，在一些地形起伏较大的山区城市中，隧道的使用愈发频繁，城市道路信号平面交叉又是城市路网中的关键节点，隧道出入口与平面交叉间的合理距离关系到整个路网车辆的通行效率以及行车安全。间距过短，在隧道出口处驾驶员可能会因隧道内外“明适应”的影响而发生行车事故；另外驾驶员容易受周边道路交通状况的影响，需要一定的时间进行分析处理，来不及反应同样对行车安全不利。

设计规范[1～2]中并没有对城市隧道路段和平面交叉之间的距离作出明确规定，仅可以参考CJJ 221—2015《城市地下道路工程设计规范》中要求城市地下道路出口接地点与信号控制交叉停车线距离不宜＜1.5倍停车视距，条件受限时不得＜1倍停车距离；但是CJJ 221—2015的规定比较模糊，并没有结合不同等级道路的设计速度、车道数给出明确的取值并且其是否适用于隧道出入口有待进一步研究；因此在实际设计中有必要建立合适的模型对隧道出入口与平面交叉间距进行深入分析研究。

1 计算模型的建立与参数的标定

隧道出入口与平面交叉之间的距离由明适应距离La、标志辨识距离Lb、车辆换道距离Lc、减速制动距离Ld和排队等候段距离Le5部分构成。见图1。

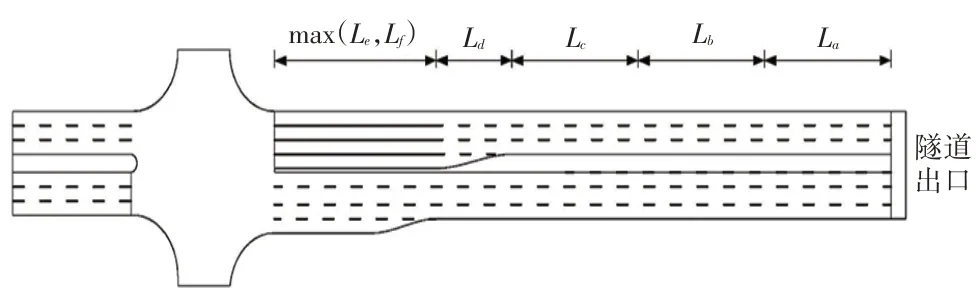
图1 隧道出口与相邻平面交叉间距计算模型

1.1 明适应距离

驾驶员长时间在隧道内行驶，人眼已经适应了隧道内的暗环境，驶出后由于内外光线强度和道路交通环境差异较大，若此处距离不够或者道路线型变化较大，就极易发生交通事故，在进行道路设计时，必须重视此部分的距离。结合车辆加减速计算公式，进行简单的三角函数分析变换，可以得到明适应距离

式中：v为城市道路的设计速度，km/h；ta为人眼适应隧道外部明亮环境所需时间，研究表明，驾驶员在长时间隧道行驶之后，若突然暴露于外部明亮的环境，最短需要1～3 s的时间才能逐步缓解外部强烈光照带来的刺激，适应外部道路交通环境，基于行车安全的考虑，本文取3 s。

根据式（1）可以得到不同道路设计速度下明适应距离，见表1。

表1 隧道出口明适应距离

1.2 标志辨识距离

通常情况下，驾驶员驶离隧道经历了隧道外的“明适应”距离之后，需要对外部道路的交通现状作出反应，才能有效避免道路交通事故的发生，此段距离称之为标志的辨识距离

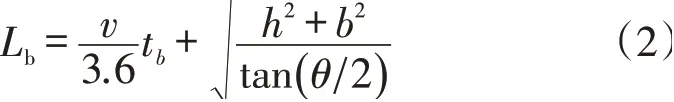
式中：v为城市道路的设计速度，km/h；tb为驾驶员对交通标志的读取反应时间，本文取值2.5 s[3]；h为驾驶员的视线高与道路交通标志牌的差值，本文取值1.2 m[4]；b为城市道路行车道的宽度值，本文取值3.5 m；θ为驾驶员视线行车时视线角度范围，本文取值5°[5]。

根据式（2）可以得到标志辨识距离的取值，见表2。

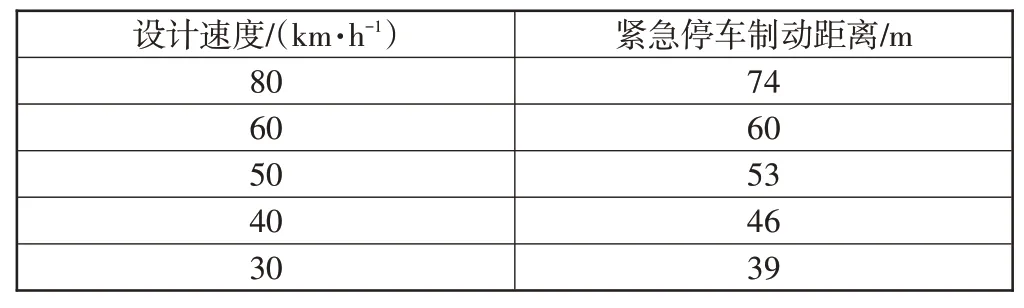
表2 标志视认距离

1.3 换道距离

研究表明[6～7]，当车速较低时，车辆变换车道行驶轨迹见图2。

图2 车辆变换车道时行车轨迹

换道距离可以按照以下公式进行计算

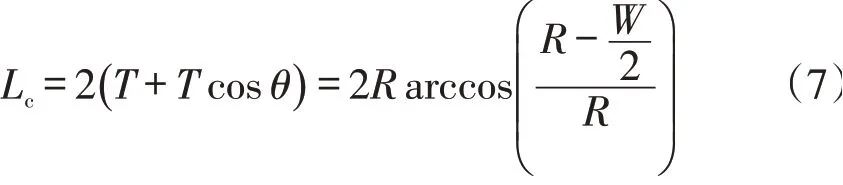
根据式（3）－式（7）可以得到不同设计速度下车辆变换一次车道所前进的距离，见表3。

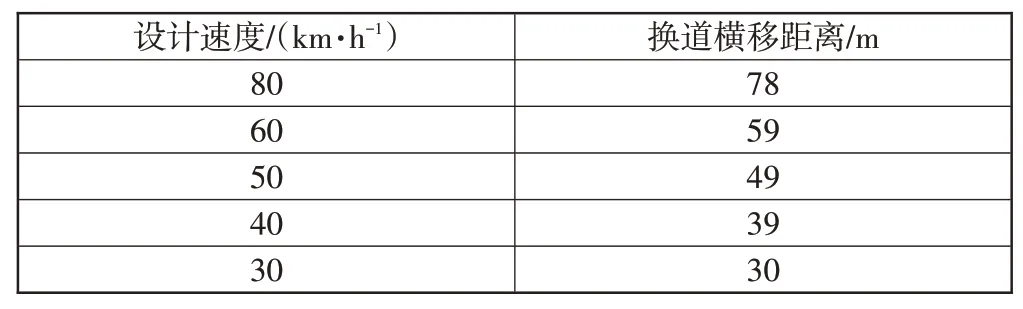
表3 一次换道车辆前行的距离

1.4 渐变段距离

左转车辆在进入左转专用车道的过程中渐变段的距离等于一次变换车道前进的距离

1.5 减速距离

车辆在进入平面交叉口时，若前方发生交通事故或恰好遇上红灯，速度可能降低到0，参考物理学中的减速公式进行简单的几何变换，可以得到车辆减速距离

式中：v为道路设计速度，km/h；α为车辆减速度，本文取2.5 m/s2[8]。

根据式（9）可以得到减速距离，见表4。

表4 减速距离

1.6 左转排队等候距离

目前的研究表明[9～10]，左转车流到达率服从泊松分布，车辆排队的概率密度

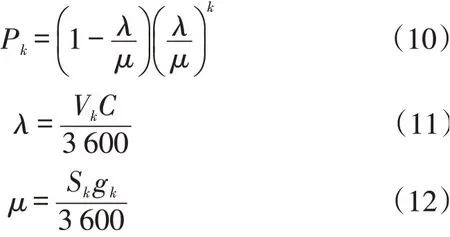
式中：λ/μ为左转车辆服务饱和度；k为排队等候的左转车辆数；Vk为设计左转交通量，pcu/h；C为信号周期长度，s；Sk为左转专用车道的饱和流率，pcu/h；gk为左转绿灯时长，s。

通过简单的积分变换，可以得到左转车辆排队数量R的概率

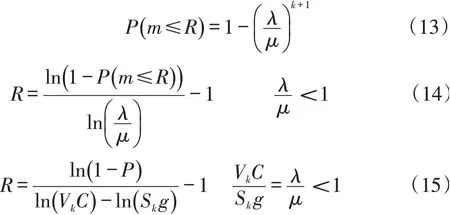
左转排队等候段距离

式中：Li为左转单个车辆的平均排队长度，本文取9 m；P（m≤R）为左转车辆排队数不超过R的概率，目前的研究表明，若城市主干道与其他等级道路相交，通常取值为98%，次干路相交为95%，次干路与支路相交取90%，支路相交取85%[9]。

在左转车辆的服务率＜0.9时，分析得到了不同服务饱和度及概率情况下，左转车辆排队等待段长度的变化曲线，见图3。

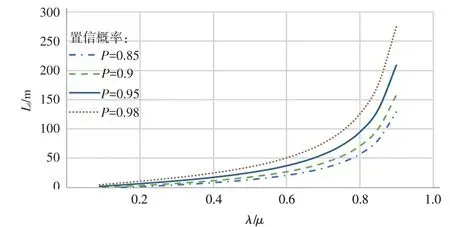
图3 排队等待段长度与服务率之间关系

在左转车辆在服务饱和度率为0.8时，计算得到左转排队等候段长度，见表5。

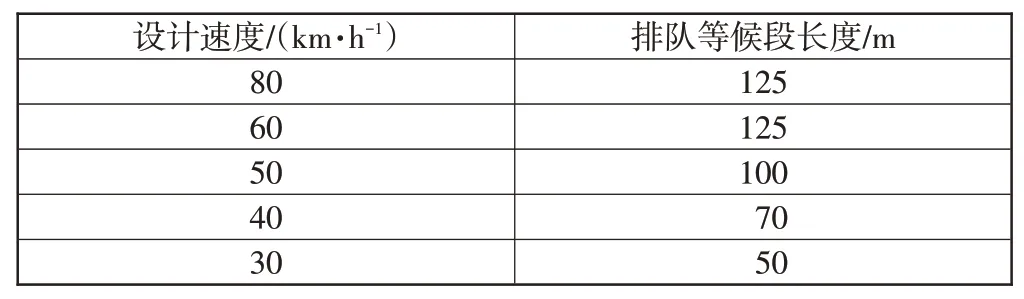
表5 左转排队等候段长度

2 计算结果分析

综上所述，城市道路隧道出口与道路平面交叉间距

式中：n为城市道路车道数。

将表1-表5结果分别代入式（17），可以得到城市道路隧道出口与平面交叉之间合理间距见表6。

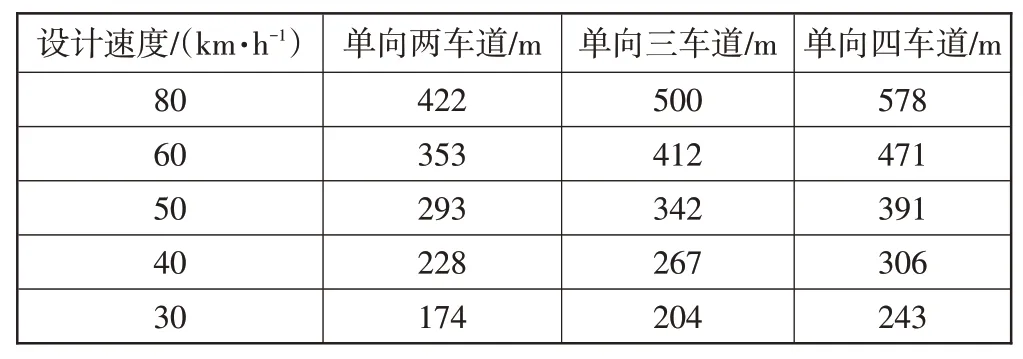
表6 城市道路隧道出口与平面交叉合理间距

3 结论

本文基于车辆加减速理论、隧道行车安全性、人眼明暗适应性、交通流理论、统计学和概率论的基本原理建立了隧道出口与平面交叉距离的计算模型，由计算结果可以发现，城市道路隧道出口与平面交叉间距和道路的设计速度、车道数紧密相关，设计速度越高、车道数越多，间距的计算值越大。

本模型中一些参数的取值参考了国外学者的研究成果，在我国是否适用有待进一步验证。实际进行城市道路隧道和平面交叉设计时，可以参考表6的计算结果，但还应当结合不同地区道路交通专项规划、道路交通现状以及驾驶员的行为习惯等资料并通过试验对上述取值进一步修正。若受实际条件限制难以满足计算值的要求时，应当增加其他安全措施，比如采用增设减速振动标线、预告警示标志牌、强化管理或者道路限速等措施。