不规则工作面开采地表沉陷线积分预计方法

滕永佳阎跃观郭伟姜岩胡耀东

1. 中国矿业大学(北京)地球科学与测绘工程学院,北京 100083；2. 山东科技大学测绘与空间信息学院,山东青岛 266590

矿山开采导致地下岩层原有的力学平衡被破坏,使地面发生沉降,损伤建筑物、水体、管道和通信输电设施等[1-2]。矿山开采沉陷预计是开采沉陷学中的基本问题。自20 世纪60年代起,基于随机介质理论[3-4]创建的概率积分法在我国得到广泛应用[5-7]。针对不规则工作面开采地表沉陷预计,已有学者基于概率积分法原理,采用各类算法对其进行了优化和改进[8-10]。张华兴、周万茂等[11-12]提出利用数学方法对概率积分法公式进行积分转换的思想；吴侃、蔡音飞等[13-14]提出利用矩形单元剖分工作面,使用概率积分法计算各单元后将预计结果叠加；许冬等[15]提出将工作面按角点剖分为梯形单元,使用变步长辛普森积分计算各单元后进行叠加处理；赵晓东等[16]提出使用非结构化三角形单元剖分工作面,采用复合辛普森积分计算地表移动变形；李永树、张兵等[17-18]提出通过划分积分区间及叠加计算处理不规则工作面；周棒等[19]通过坐标系转换,实现了在计坐算标系中不规则工作面边界的自动确定。这些方法的预计过程中往往需要使用不同几何单元剖分工作面及转换坐标系等,计算量较大,且几何单元的大小对预计结果精度有一定影响。

本文针对上述问题,开展了不规则工作面开采地表沉陷预计线积分方法的研究工作,该方法简单易行,可为“三下”开采沉陷预计提供算法依据。概率积分法是开采沉陷预计的重要方法,但对于不规则工作面开采,其预计精度有待提高。本文利用格林公式(Green formula)对概率积分法公式进行积分转换,将对工作面的积分转换为对采区边界的线积分；将边界简化分割为多条直线段,分别对各直线段作积分计算；通过叠加计算完成地表任意点及地表沉陷盆地移动变形预计。

1 理论基础

概率积分法和格林公式是本文提出的不规则工作面开采地表沉陷线积分预计方法的理论基础。其中,概率积分法是开采沉陷预计的重要方法,其本质是单元开采影响函数对工作面区域的积分；而格林公式的作用是进行线面积分的相互转换,利用其可以将概率积分法公式由面积分转换为针对开采工作面边界的线积分。因此,在计算过程中合理分割工作面边界,即可提高不规则工作面开采地表沉陷的预计精度。

1.1 概率积分法

基于随机介质理论,从统计学的观点出发,可将整个采区分解成无数个微小单元,通过计算所有单元对岩层和地表影响的总和,即可得到整个采区开采引起的地表移动和变形值。此计算过程可以用概率积分法[6-7]完成,地表任意点的下沉预计值计算如下:

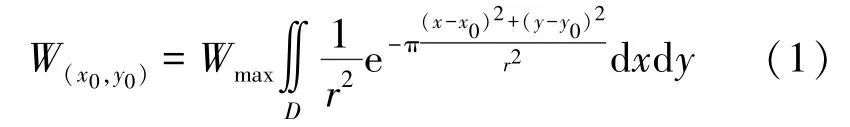
式中,W(x0,y0)为(x0,y0)位置处地表下沉预计值；Wmax为充分采动条件下地表最大下沉值；D为开采工作面区域(积分区域)；r为主要影响半径。

1.2 格林公式

格林公式广泛应用于数学、工程、物理等相关专业,其在积分问题上的主要作用是将函数在区域内部的面积分与区域边界上的线积分相互转化[20-21]。格林公式的使用条件为,当区域D是单连通区域,函数P(x,y)、Q(x,y)在D上具有一阶连续偏导数时,则有

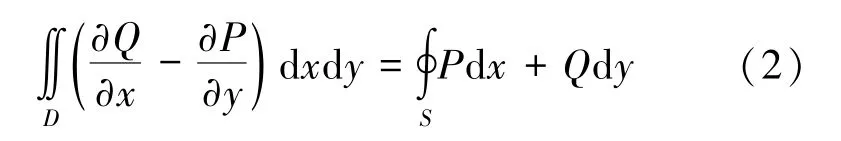
式中,S为积分区域D的边界。

2 开采沉陷线积分预计方法的构建与实现

2.1 方法原理与构建

现代采煤技术中,工作面一般为矩形工作面,而在某些条件下,如在某些老采空区作业或地质结构复杂时,实际开采工作中容易出现多边形工作面,即不规则工作面,如图1 所示。

图1 不规则工作面示例Fig.1 Examples of irregular shaped working face

处理不规则工作面的一般方法如图2 所示。若使用矩形单元剖分工作面,单元大小会影响工作面边界处地表变形预计精度。若矩形单元较大,则工作面边界容易出现“锯齿”现象,这种情况下预计精度较低；若减小矩形单元面积,则预计精度提高,而计算效率大大降低。因此,应寻求一种同时兼顾边界精度和简化计算过程的地表变形预计方法。

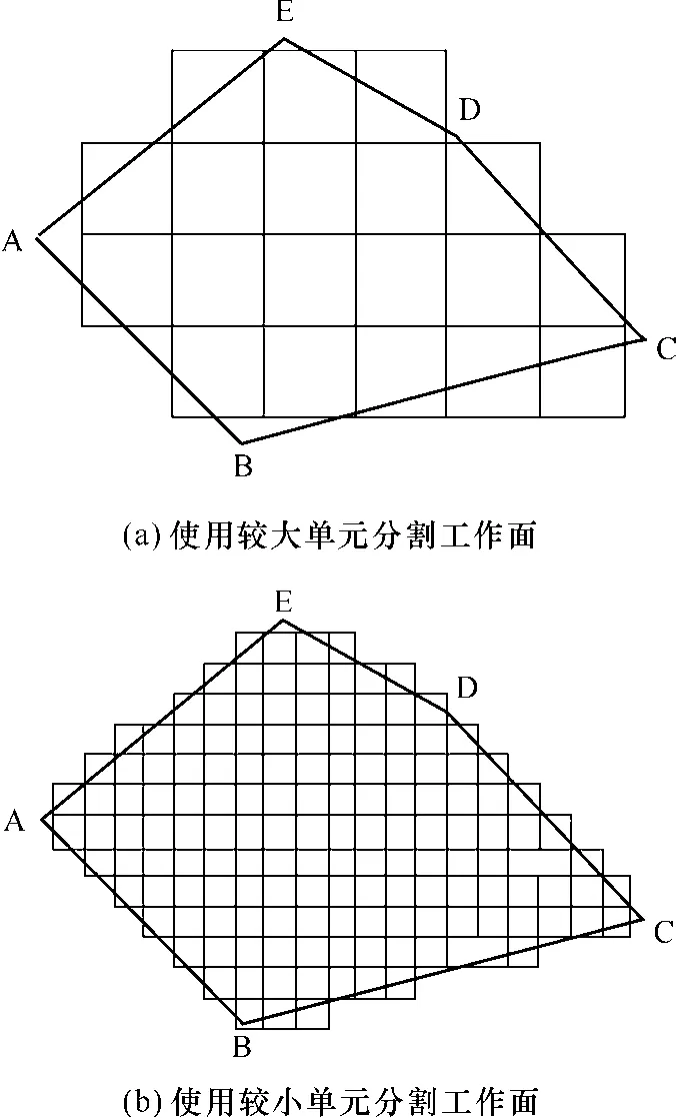
图2 矩形单元剖分方法Fig.2 Rectangular element division method

概率积分法本质上就是单元开采的影响函数对开采工作面区域的积分。因此,结合格林公式的原理,使函数P(x,y)、Q(x,y)既能满足在区域D上具有一阶连续偏导数的条件,又能满足式(3),即

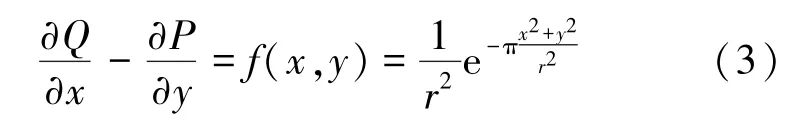
就可以将概率积分法公式转化为线积分形式:

假设函数:

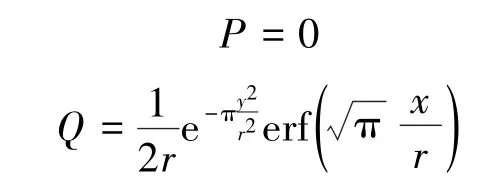
则地表任意点的下沉预计值计算如下:

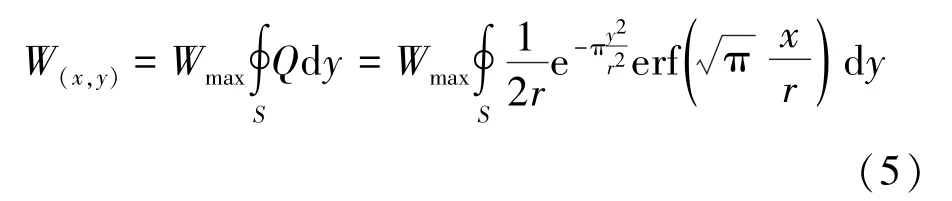
2.2 工作面边界简化方法

工作面边界简化方法如图3 所示。在实际计算中,一般可认为工作面由多条直线段首尾相接围绕而成。

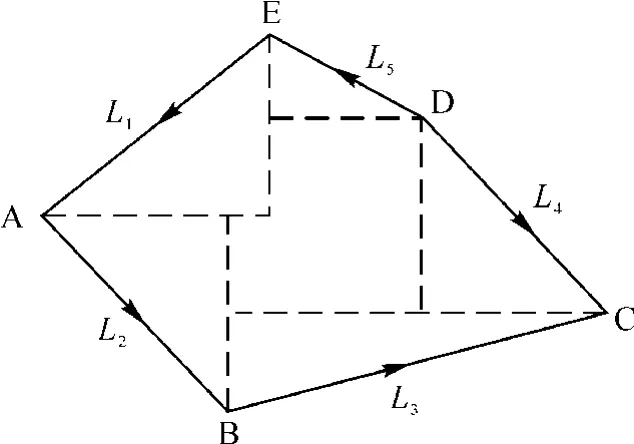
图3 工作面边界简化方法Fig.3 Simplification method of working face boundary

由线积分的计算原理可知,将边界划分为有限条直线段,方向为逆时针,由于积分结果只与线段起点和终点有关,与路径无关,所以可将各段向x、y方向分解,独立计算x、y方向的积分。当计算x轴方向积分时,由于dy=0,则对该方向积分结果为0,进一步简化了计算过程。工作面开采预计结果,可由各段积分结果叠加计算得到。于是地表任意点变形值的计算转化成采区边界的线积分计算,得到不规则工作面开采地表任意点下沉预计的线积分法公式如下:

式中,Li为组成工作面边界的各直线段；(x0,y0)为待预计点的坐标。

根据概率积分法中地表倾斜、水平移动、水平变形与地表下沉之间的数学关系,可推导出不规则工作面开采地表倾斜、水平移动和水平变形公式如下:

地表倾斜预计公式:

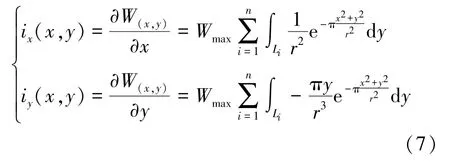
水平移动预计公式:

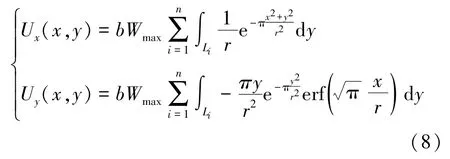
水平变形预计公式:

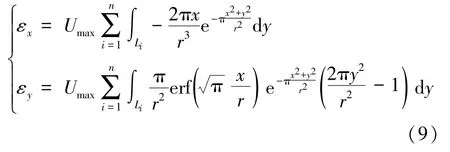
2.3 方法流程实现

为实现不规则工作面开采预计地表下沉的目的,结合计算机技术与相关原理,使用MATLAB 进行开采沉陷预计的流程化处理(图4)。

图4 程序流程Fig.4 Program flow

处理流程分为4 个阶段:

(1) 数据准备。从已有资料中获取采区工作面边界坐标、地表变形预计参数,并以格网划分地表待预计区域。

(2) 根据工作面信息确定积分区域与开采工作面边界,结合边界简化与分割方法,确定工作面区域并分割工作面边界。

(3) 叠加计算。获取工作面边界各端点坐标后,分别对每个格网点进行计算并将各段结果叠加,最后得到全部点的下沉预计值。

(4) 输出结果。可将结果组织成文件并绘制成图,获取地表下沉盆地形态与特征,便于进行地表三维模型建立、地表建筑物损坏分析、矿区生态环境治理等工作。

3 应用实例对比分析

分别使用矩形单元分割法和线积分法,对峰峰矿区某工作面开采地表下沉进行预计,与实测数据进行对比分析。峰峰矿区某矿于2016—2017年开采2141、2143 工作面,工作面水平投影为不规则多边形(图5)。平均开采深度为600 m,平均采高为4.2 m,煤层倾角为18°,下沉系数为0.75,主要影响角正切为2.0。

图5 不规则工作面与地表Z 观测线位置Fig.5 Location of irregular working face and Z observation line

实际观测值、线积分法和概率积分法预计结果如图6 所示。三者的对比情况见表1。由表1 可知,对远离工作面的观测站,线积分法和概率积分法预计结果精度相当,而在接近工作面边界处,线积分法的预计结果更接近实测值,精度高于常规的概率积分法。

表1 预计与实测结果对比Tab.1 Comparison between expected and measured results

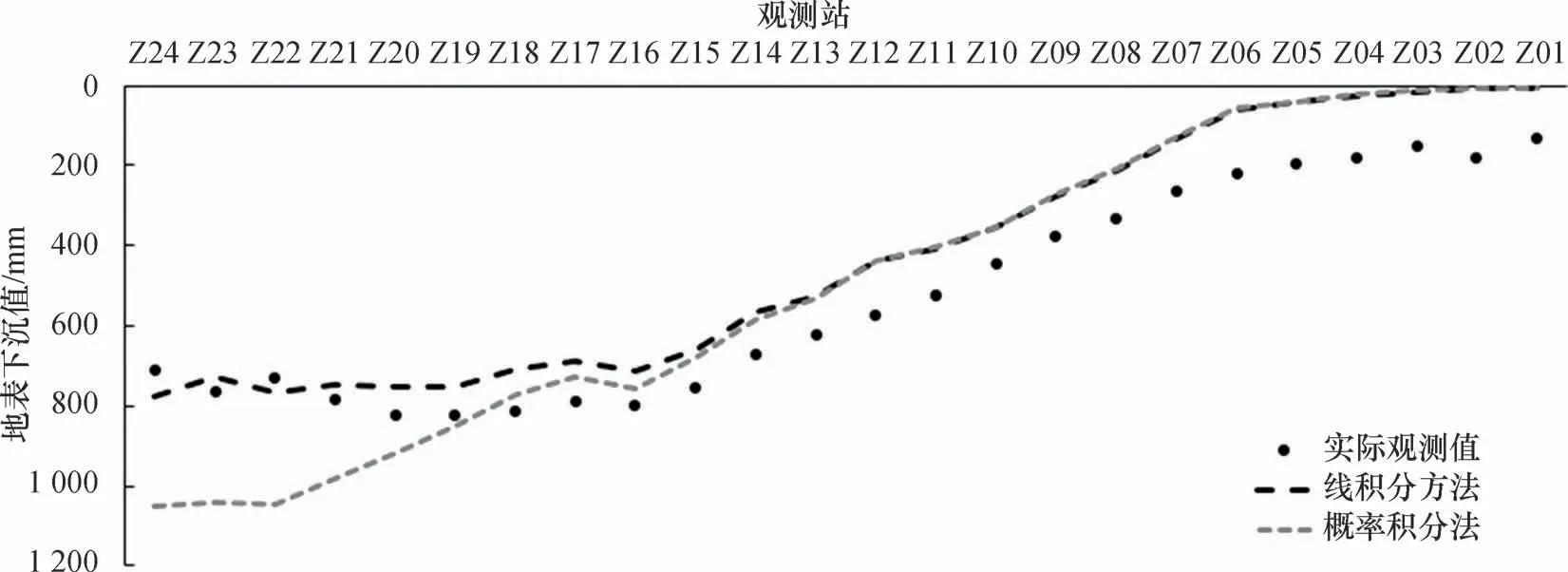
图6 实测值与预计结果Fig.6 Measured value and expected result

线积分法和概率积分法预计结果的精度评定见表2。由表2 可知,本文线积分法预计结果更接近实测值,精度优于概率积分法。根据两种方法的RMSE 值,线积分方法预计精度相比概率积分法提高了23% 。

表2 精度评定Tab.2 Assessment of accuracy

4 结 论

(1) 针对原有方法在不规则工作面开采预计方面的不足,使用格林公式对概率积分法公式进行积分变换,提出线积分法公式。该方法将求取工作面开采造成的地表下沉值,转化为求取工作面边界的线积分计算值。

(2) 提出边界分割与简化方法。将工作面边界分割为多条首尾相接的直线段,简化了工作面的处理过程,避免了单元分割方法中常见的“锯齿状”边缘及积分单元分割过程复杂的问题。

(3) 通过实例对比线积分法和概率积分法地表下沉预计结果,表明线积分法改善了原有方法对工作面边缘计算不准确的问题,能够为“三下”开采沉陷预计提供依据。