基于频变阻尼特性的四参数隔振系统建模与参数分析
蒲华燕,何文元,孙 翊,丁基恒,罗 均,谢少荣,彭 艳,王 敏
(上海大学 机电工程与自动化学院,上海 200444)
传统被动隔振器通常是由弹簧和黏性阻尼器并联组成的两参数隔振系统。由于其具有控制简单、稳定性好,且不需要外部电源等优点,广泛用于航天工程[1-6]等领域。但近年来,随着轨道卫星、遥感卫星搭载的任务载荷精度不断提升,其对振动环境的要求也不断提高。加之,轨道卫星、遥感卫星等在轨运行时存在极强的微振动、微重力环境,其具有振幅小、频带宽等特点,多为频率范围在0.1~300 Hz的谐波干扰[7-8]。因此,对高精度有效载荷免受微振动影响提出了更高的性能挑战[9-18]。
传统两参数被动隔振系统通过阻尼调节消耗微振动能量实现隔振。当阻尼较大时,共振峰处的振动得到有效抑制,但是高频段隔振性能变差,无法有效保证太空载荷高频振动衰减的快速性;当阻尼较小时,高频段隔振性能较好,但是共振峰不能得到有效抑制,从而诱发太空载荷低频共振,甚至对载荷设备造成破坏。因此,对于航天器中的特殊微重力、微振动环境,两参数被动系统在共振频率和高频的隔振性能存在固有的相互矛盾,无法有效满足实际使用需求。
为了解决两参数被动系统的相互矛盾,需要一种同时具有低频大阻尼、高频小阻尼的隔振系统,即系统阻尼会随着频率的增大而减小,从而实现低共振峰值和良好的高频隔振性能,具备此特性的系统定义为频变阻尼系统。频变阻尼系统由于能够同时保证共振区和高频段的隔振性能,具有广泛的研究前景。
因此,在两参数被动系统的基础上,为了探索频变阻尼特性,三参数被动系统的隔振器被设计和研究。三参数系统由弹簧和弹性支撑的阻尼器并联组成,可以通过合理调节参数值调谐系统,使其隔振性能优于两参数系统。曾有学者对基于三参数的被动隔振系统进行了尝试,初次尝试结果表明,三参数系统在防冲击方面表现出明显的优势。但是,随着主动反馈控制算法的提出[19-20],有效的从源头上克服了两参数被动系统在低频隔振性能与高频衰减性能之间的矛盾,三参数被动系统的研究停滞了很长时间。
随着航天技术的快速发展,航天器中的任务载荷对隔振器的可靠性、稳定性要求越来越高,由于主动隔振技术需要输入外部能量且控制结构复杂、不稳定,这两点很大程度上限制了其在航天领域的应用。于是,很多学者重新开始研究三参数被动系统。例如,Liu等[21]开发了一种基于三参数系统的流体黏性阻尼器,性能优于传统被动隔振器。Brennan等[22]研究了三参数系统在自由振动和强制振动下的动力学行为,确定和比较了系统在不同类型的激励下的最佳阻尼值,作者指出,对于简谐激励来说,系统具有较好的隔振效果;当系统被白噪声激励时,附加弹簧没有表现出明显的优势。王超新等[23]给出了一种三参数隔振系统在最优阻尼下的设计方法。焦小磊等[24]提出了基于归一化模型的三参数隔振系统优化设计方法,对共振峰和高频衰减率进行了多目标优化设计。Zhang等[25-26]研究了基于三参数系统的隔振平台的性能,提出了基于频域特征的隔振平台参数设计方法和流程。王杰等[27-28]提出一种确定三参数模型阻尼系数的机械阻抗等效理论与测试方法,将三参数模型简化为等效的便于试验测试的两参数隔振模型,得到了以往传统方法难以得到的动态阻尼系数随频率的变化规律。Silva等[29]研究了三参数模型中用非线性立方弹簧代替主弹簧的影响,结果表明,当立方刚度属于软化类型时,可以改善隔振器在共振频率附近和高频的传递率。Wang等[30]指出了三参数模型中非线性次级弹簧的使用能够较好地改善系统高频和共振频率处的隔振性能。以上研究主要侧重于三参数系统隔振性能的优化设计和分析,而很少考虑阻尼器和次弹簧之间实际存在的等效质量对系统性能带来的影响。
因此,提出了一种基于频变阻尼特性的四参数隔振系统,并对其进行系统建模与参数分析。提出的四参数隔振系统是一种基于三参数系统的等效模型,在阻尼器和次弹簧之间附加一个中间等效质量,从而叠加形成四参数系统。通过归一化参数,建立四参数系统的理论模型,分析各参数对系统隔振性能的影响,提出一种基于四参数系统参数优化的思路,并从频域和时域上分析了系统的隔振性能,在扫频信号激励下,通过MATLAB/Simulink模拟仿真,验证了系统理论计算模型的准确性。
1 四参数系统模型
1.1 模型描述
本文研究的四参数系统为单自由度系统,系统等效模型是基于两参数系统模型和三参数系统模型,如图1(a)和图1(b)所示。
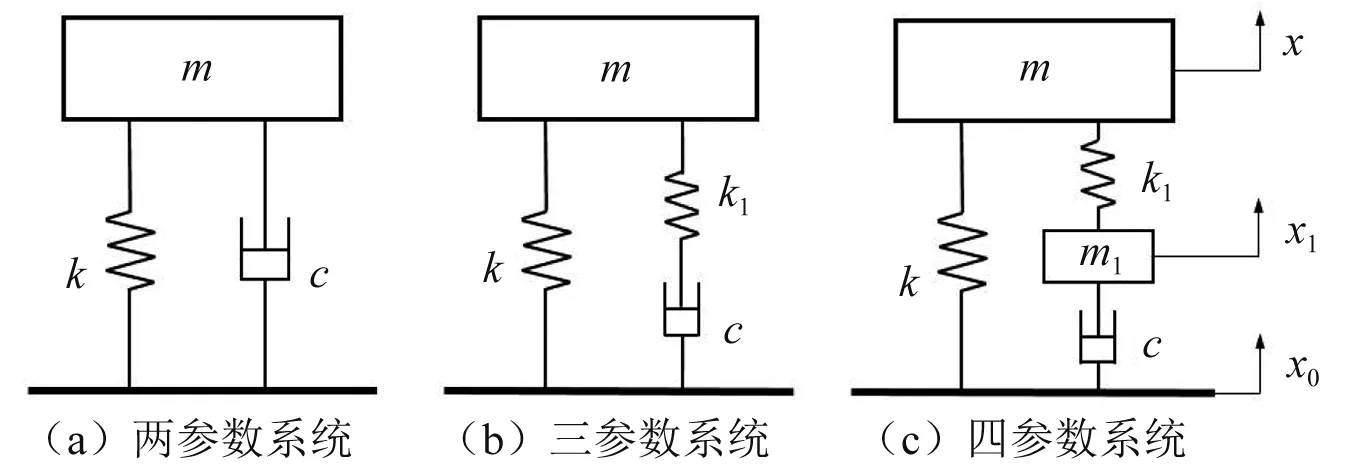
图1 等效模型
四参数系统中负载质量m由主弹簧k和黏性阻尼器c并联组合支撑,阻尼器c、中间等效质量m1和次弹簧k1依次串联组合,如图1(c)所示。
1.2 模型建立
根据牛顿运动定律,可以得到四参数系统的运动方程组
(1)
(2)
式中:x0为基础位移;x1,x分别为中间等效质量和负载质量的位移。
对参数进行归一化处理,令N=k1/k,P=m1/m,其中:N为刚度比;P为质量比,且均为正实数。对式(1)变换,得到中间等效质量的位移
(3)
对式(3)在时间上求导两次,可得到
(4)
(5)
综合式(2)~式(5),得到四参数系统的四阶常微分方程
(6)
(7)
对式(7)两边同时进行拉普拉斯变换,可以得到
(8)
根据传递率定义,将系统输出信号X(s)与输入信号X0(s)取比值,即可得到系统传递率
(9)
对式(9)进行傅里叶变换,将s=jω(其中j2=-1)代入式(9)中,则系统的传递率可表示为
(10)
式中,Ω=ω/ω0为频率比,ω为外部激励频率。传递率的幅值可定义为
(11)
另外,四参数系统的传递率模型可等效为
(12)
综合式(9)和式(12),可得到四参数系统的等效阻尼
(13)
2 参数N,P和ζ0对系统性能的影响
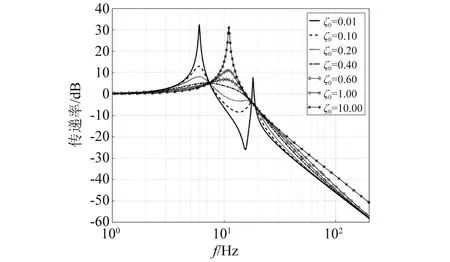
根据以前的经验,初取ζ0=0.4,ω0=2π×7。首先,利用MATLAB软件分析N和P对系统频域性能的影响,得到N和P的较优取值范围;然后,保持N和P的优化取值不变,分析阻尼比ζ0对系统传递率特性的影响。性能指标为共振峰值大小和高频衰减率。通过优化参数,使四参数系统具有近似理想频变阻尼系统的特性,如图2所示。
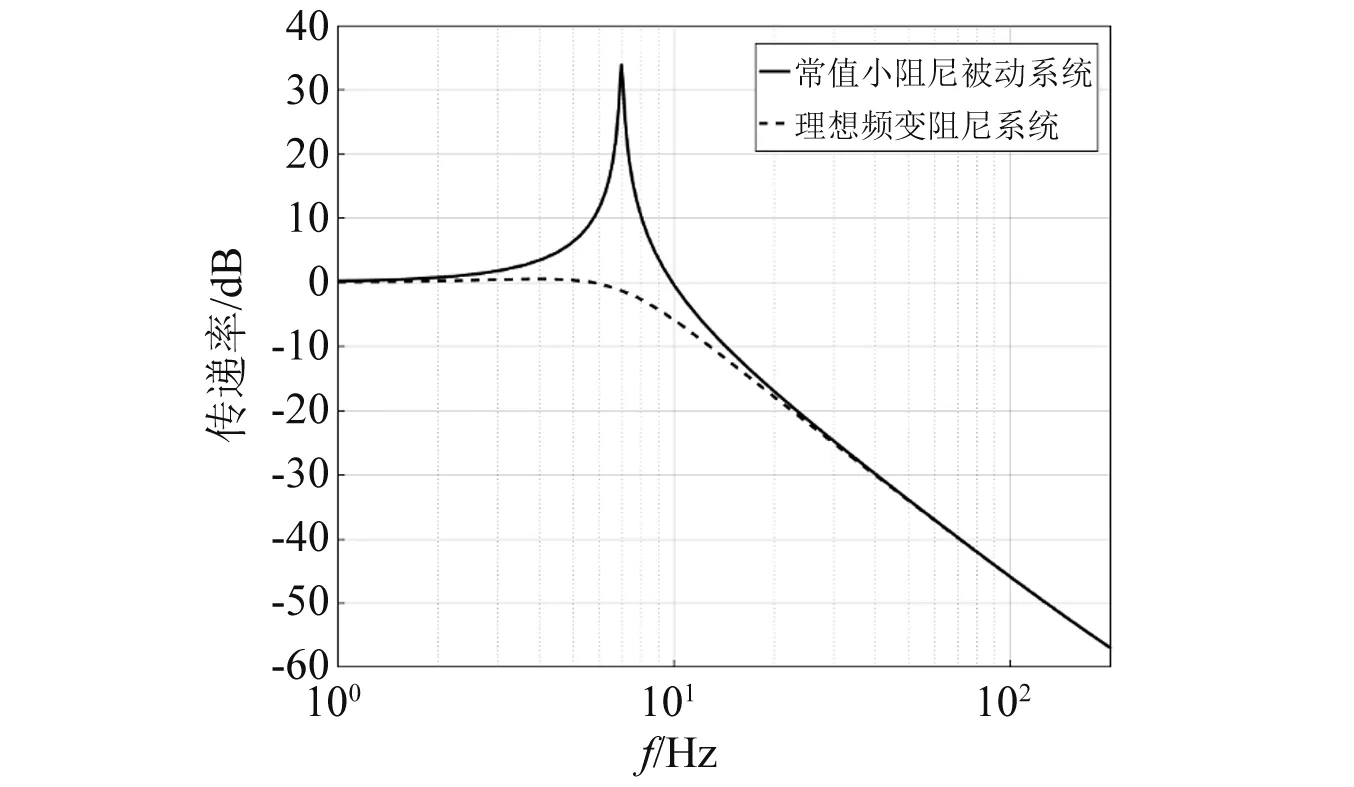
图2 频变阻尼特性曲线
2.1 情况1:P不变,N增大
保持P不变,分析N对系统性能的影响。其中P分两种情况考虑:0
P分别等于0.5,2.0和5.0,N从0.1增大到5.0时系统的频域响应,如图3所示。从图3可知,当N增大时,系统共振峰值降低,同时系统固有频率右移。
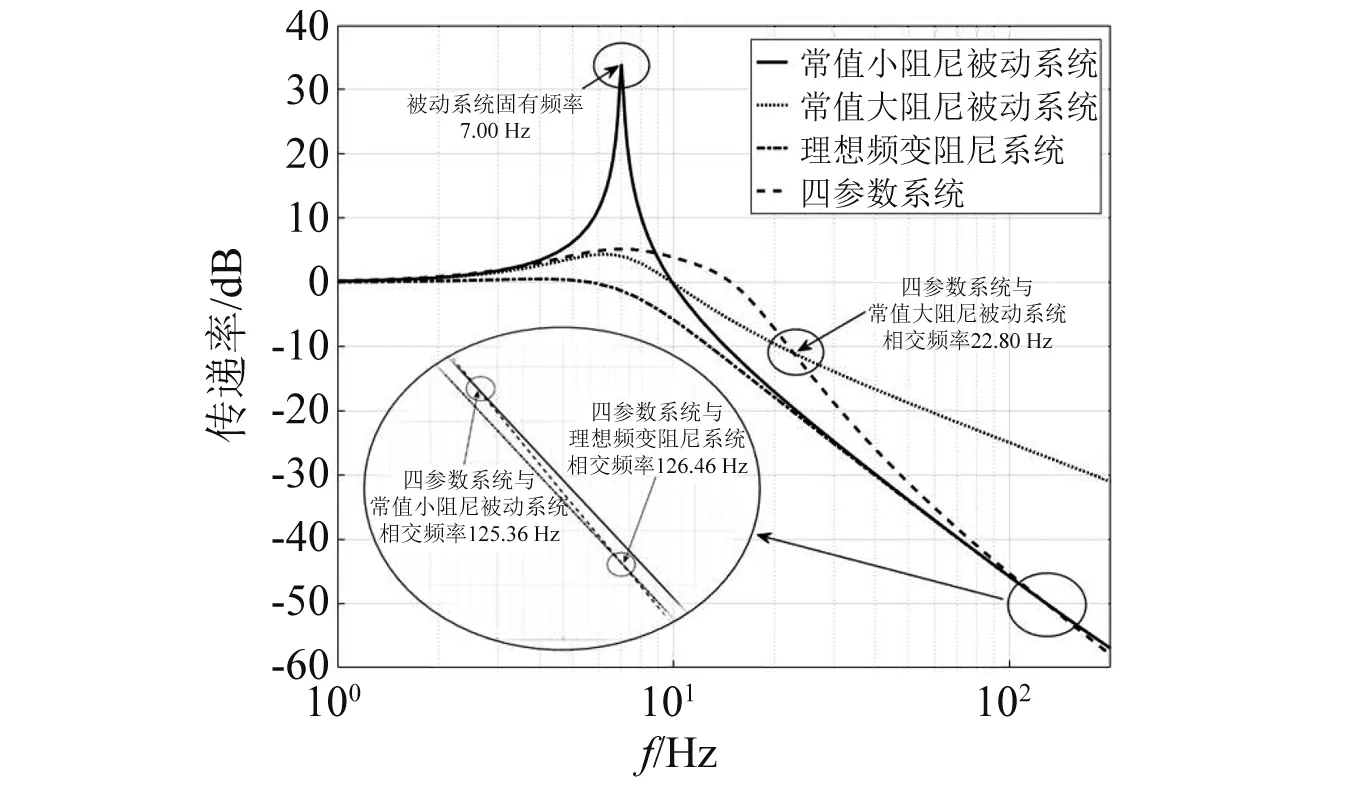
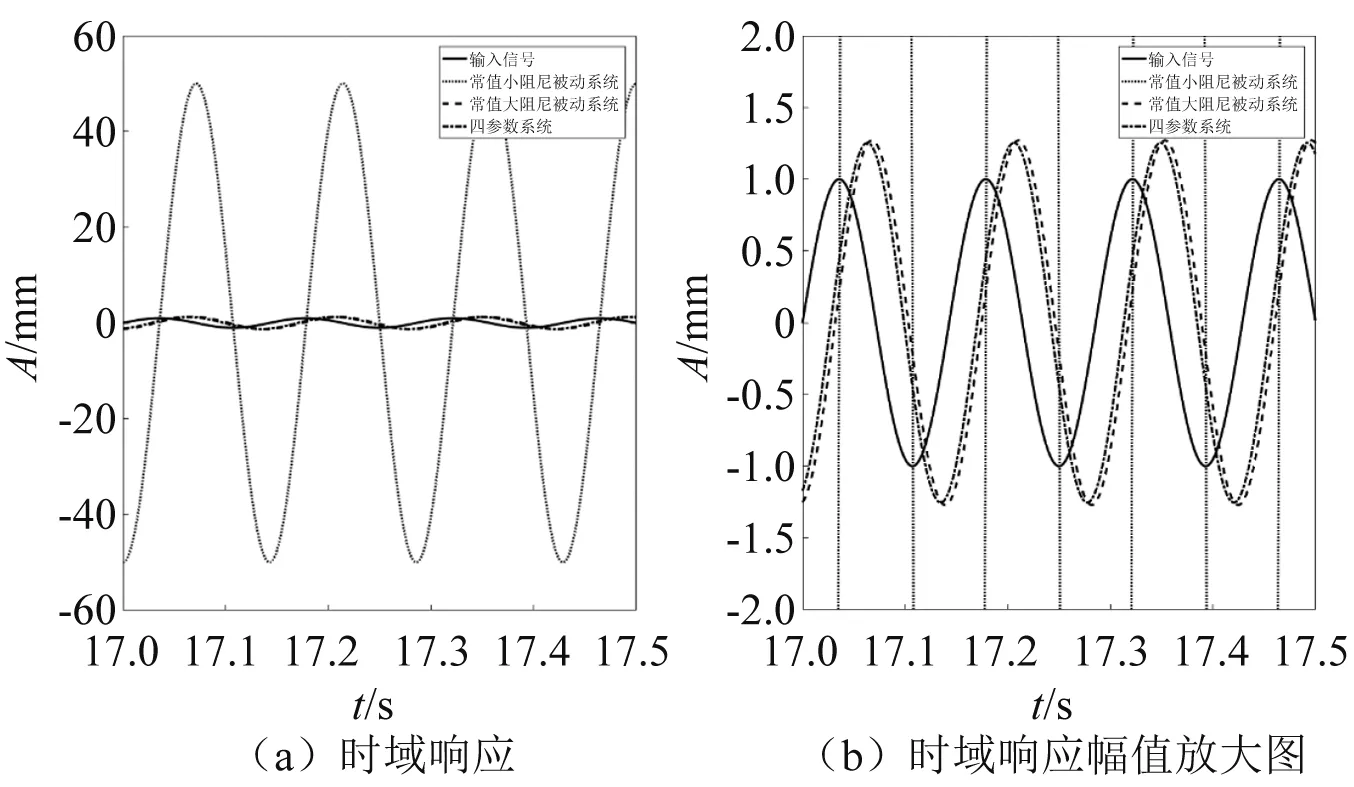
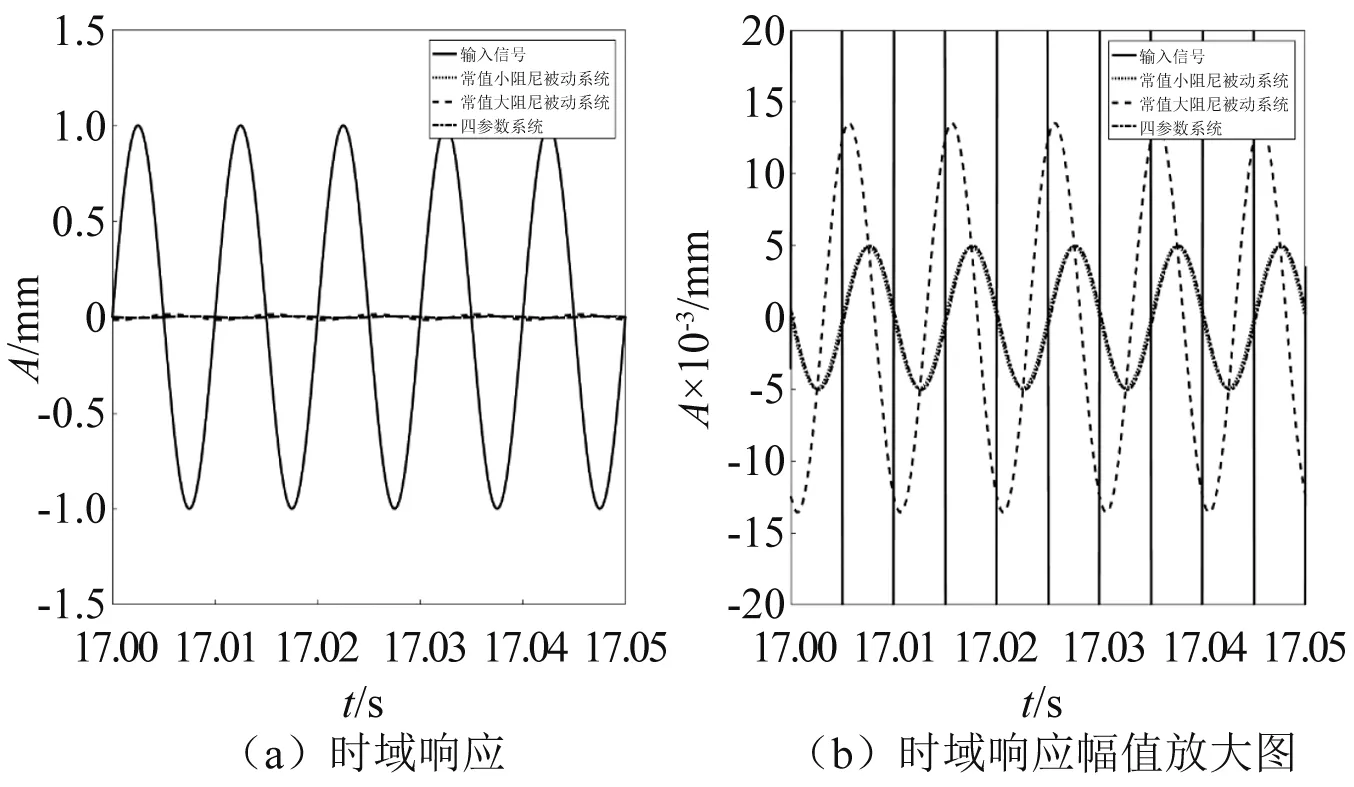
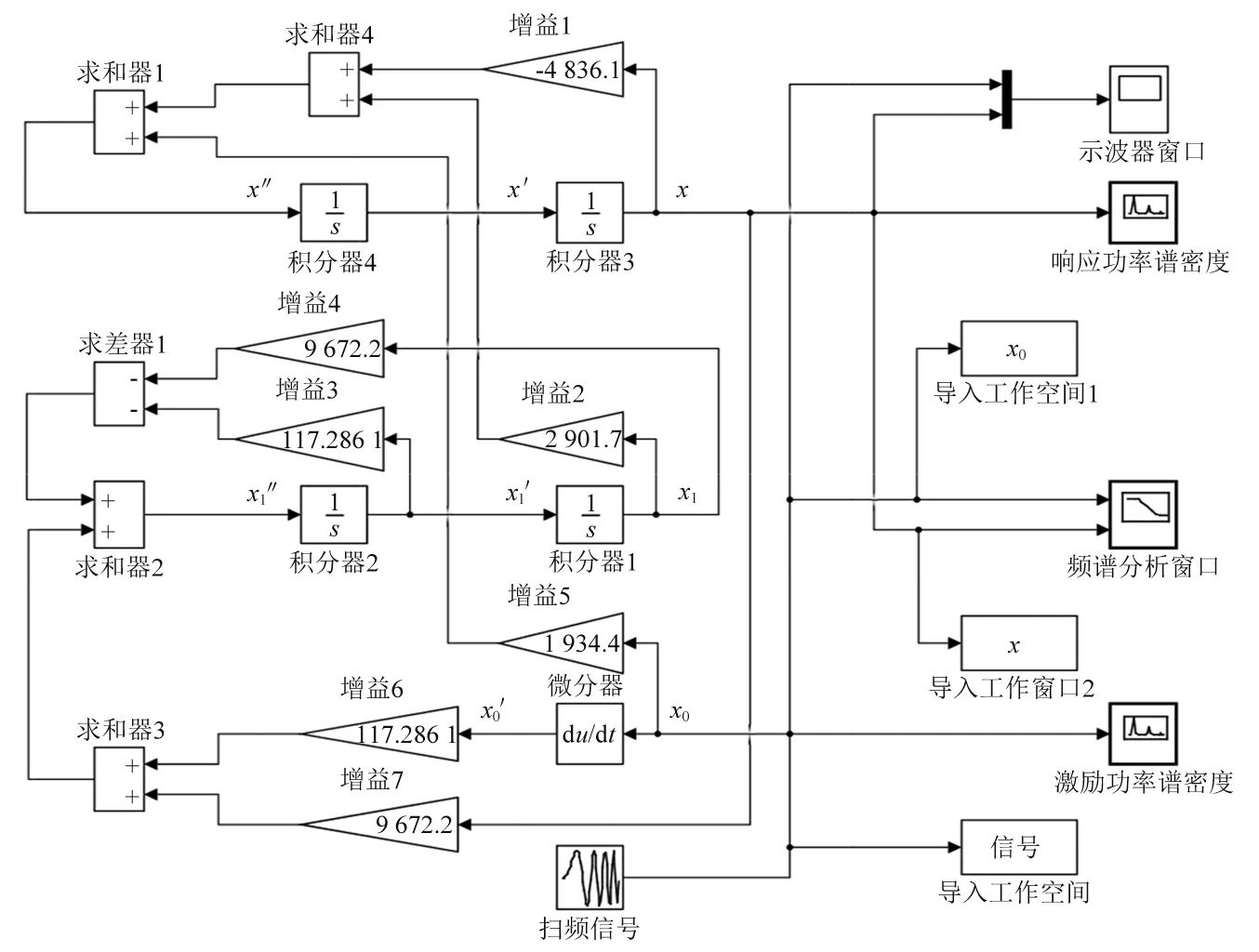
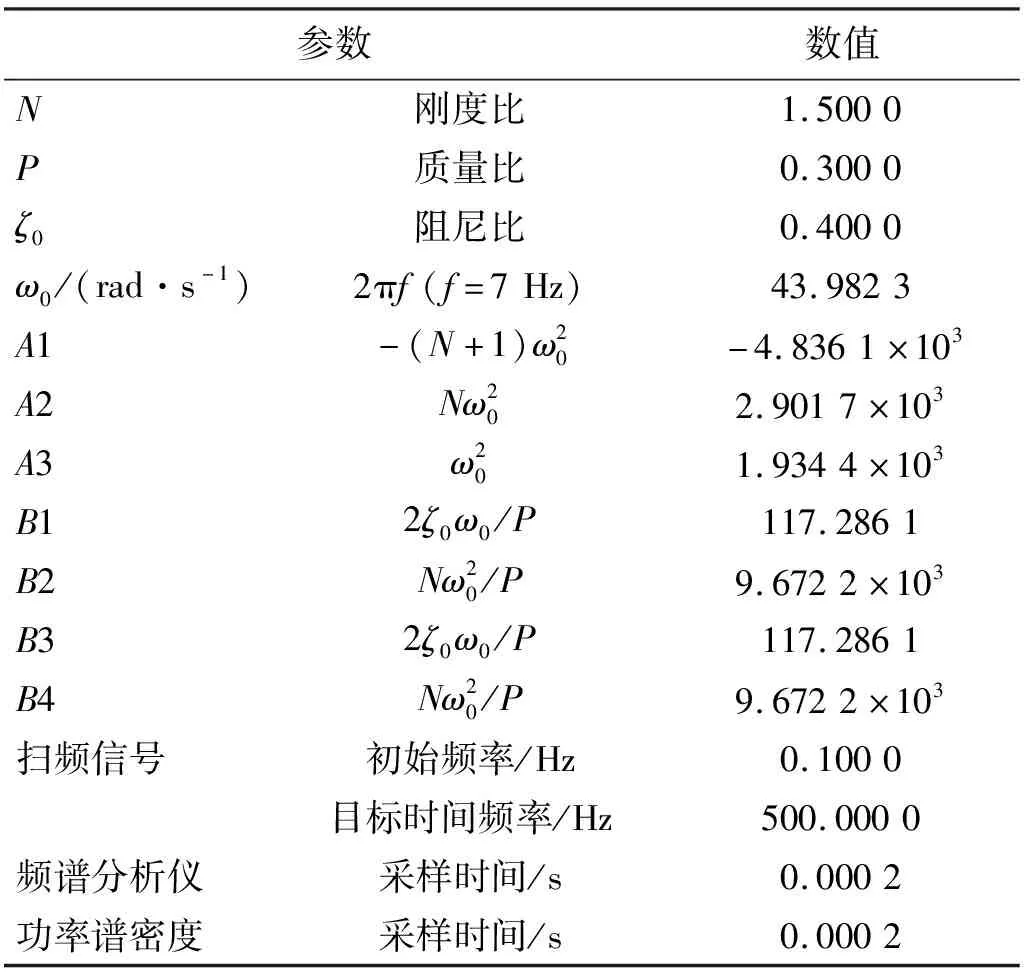
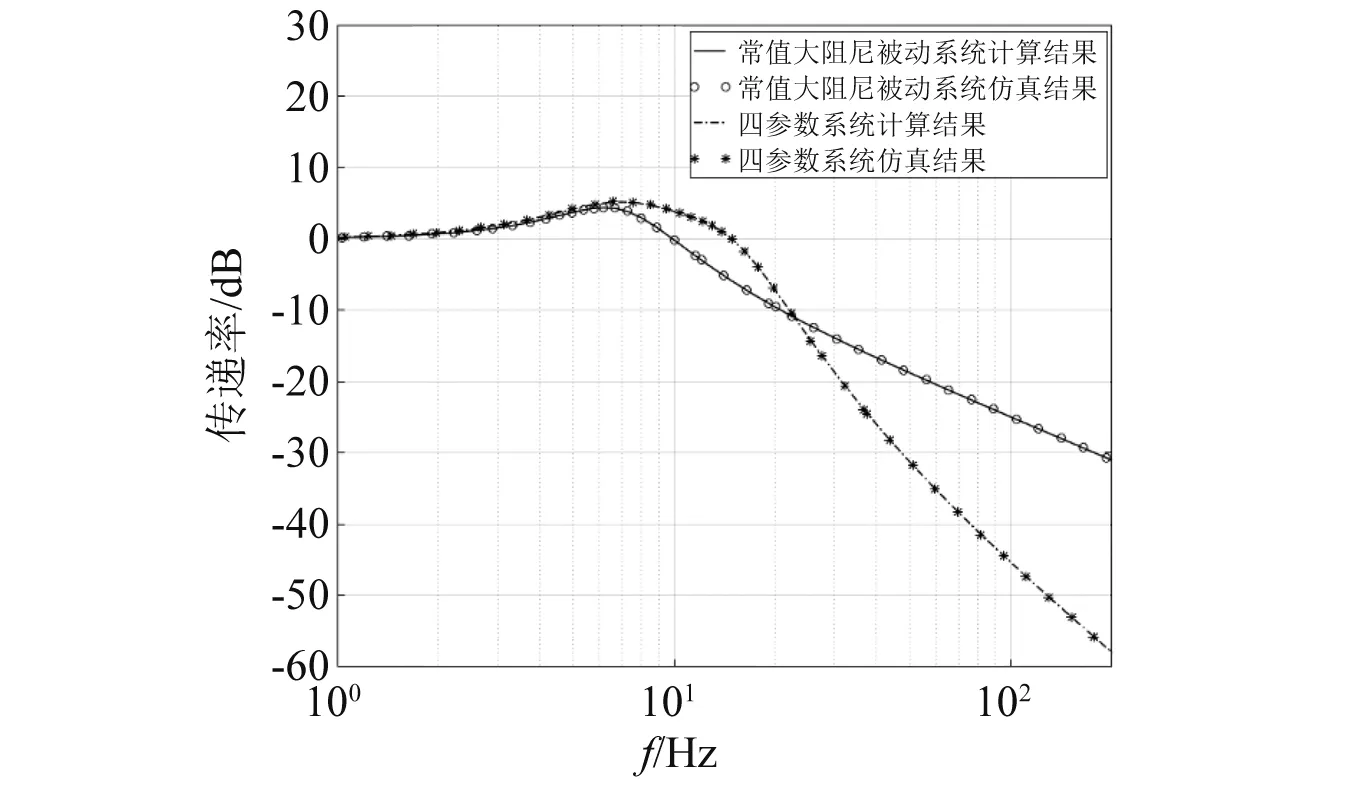
对比图3(a)、图3(b)和图3(c),当P增大时,相同N值下系统传递率幅值会随之增大,并在低频出现新的峰,这是由中间等效质量m1增大引起的。当P在0 当N的取值范围约为1.0 图3 质量比常值时的频率响应 分析N=1.5时,P(其中0 图4 刚度比常值时的频率响应 图4(a)为N= 1.5,P从0.1增大到0.9时系统的频域响应。从图4(a)可知,共振峰值随P的增大而降低,系统高频衰减率随P增大而增大。但是在共振频率往右的某一频率点后,当P>0.3时出现一个新的峰,并且峰值随着P的增大而增大; 由图4(a)可知,为了使系统具有近似理想频变阻尼的特性,P的取值范围可缩小为0.1 当P=0.2时,6~11 Hz频段的峰值较高;当P=0.4时,11~20 Hz频段的峰值较高。因此,综合以上两种情况,为了使系统在整个频段内(6~20 Hz)的传递率幅值较低,选择参数P=0.3。 当P=0.3时,对N在1.0 由2.1节和2.2节可知,刚度比N主要影响系统共振处的性能,质量比P主要影响系统高频衰减性能。 系统在不同阻尼比ζ0下的传递率特性,如图5所示。从图5可知,系统共振峰值最初随着ζ0的增大而减小,然后又增大,但共振峰出现在更高的频率处。当阻尼比ζ0趋于零时,系统传递率曲线出现两个峰,并且峰值逐渐增大。出现双峰是由于四参数系统属于四阶系统,当参数取值通过临界值时,系统频域响应表现出双共振峰现象。双峰的幅值大小受系统阻尼c变化的影响,当系统阻尼c变小时,双峰的幅值增大,此时四参数系统可等效为两个二阶系统的叠加,其中负载质量m和主弹簧k组成主要二阶系统,中间等效质量m1和次弹簧k1组成次要二阶系统,次要二阶系统相当于一个吸振器。 图5 不同阻尼比ζ0下的系统传递率特性 根据图5可得,当N=1.5,P=0.3,阻尼比ζ0在0.4附近取值时,系统可同时实现低共振峰值和良好的高频隔振性能,此时系统处于欠阻尼状态。 经过第2章的讨论和分析,得到了N,P和ζ0的较优取值范围。本节从频域和时域上对四参数系统进行性能分析。 两参数被动系统的传递率为 (14) 取N=1.5,P=0.3,ζ0=0.4,ω0=2πf(f=7 Hz),利用MATLAB软件可得到不同系统的频域响应,如图6所示。 图6 不同系统的频域响应 从图6可知,四参数系统能够较好地解决被动系统的矛盾,并且同时保持低共振峰值和良好的高频衰减率。由于四参数系统存在次弹簧k1,系统总刚度大于被动系统,因此,四参数系统的固有频率发生了右移。 将各系统的频域响应数据根据图6列于表1中。其中,7.00 Hz为被动系统的固有频率,22.80 Hz,125.36 Hz,126.46 Hz分别为四参数系统与常值大阻尼被动系统、常值小阻尼被动系统、理想频变阻尼系统的相交频率。 表1 不同系统的频域响应 相较于常值小阻尼被动系统的共振峰幅值34.00 dB,常值大阻尼被动系统能够明显降低共振峰幅值至4.04 dB,衰减了29.96 dB,但高频的隔振性能却损失了,具体如:22.80 Hz处由-19.64 dB上升至-11.04 dB,性能下降了8.60 dB;125.36 Hz处由-49.57 dB上升至-26.96 dB,性能下降了22.61 dB;126.46 Hz处由-49.71 dB上升至-27.04 dB,性能下降了22.67 dB。 相较于常值小阻尼被动系统的共振峰幅值34.00 dB,四参数系统能够明显降低共振峰幅值至5.15 dB,衰减了28.85 dB,同时高频的隔振性能随频率增大而变好,具体如:22.80 Hz处由-19.64 dB上升至-11.04 dB,性能下降了8.60 dB;125.36 Hz处两个系统均为-49.57 dB,性能一致;126.46 Hz处由-49.71 dB下降至-49.73 dB,性能上升了0.02 dB。 相较于常值大阻尼被动系统的共振峰幅值4.04 dB,四参数系统的共振峰幅值仅上升了1.11 dB,但是高频的隔振性能得到较大提升,具体如:22.80 Hz处两系统均为-11.04 dB,性能一致;125.36 Hz处由-26.96 dB下降至-49.57 dB,性能上升了22.61 dB;126.46 Hz处由-27.04 dB下降至-49.73 dB,性能上升了22.69 dB。 综上,相较于常值小阻尼被动系统,四参数系统共振峰幅值降低28.85 dB,比常值大阻尼被动系统共振峰幅值仅低约3.70%;相较于常值大阻尼被动系统,四参数系统在126.46 Hz的高频隔振性能提升了22.69 dB,比常值小阻尼被动系统高频处的性能高约0.09%。同时,以理想频变阻尼系统频域响应作为参考,当频率从7.00 Hz增大至126.46 Hz时,两个系统传递率幅值差值从6.48 dB先增大后减小至0,表明四参数系统隔振性能随频率增大而逐渐接近于理想频变阻尼系统特性。因此,四参数系统能够较好地解决被动系统高低频隔振性能之间的固有矛盾,具有低频大阻尼、高频小阻尼的频变阻尼特性。 正弦信号激励时域响应如图7所示。图7(a)为在共振频率处,7.00 Hz正弦信号激励下的时域响应;图7(b)为共振频率处时域响应的放大图。从图7可知,当输入信号幅值为±1.00 mm时,四参数系统和常值大阻尼被动系统的时域响应基本一致,幅值在±1.00~±1.50 mm,常值小阻尼被动系统的时域幅值在±40.00~±60.00 mm,表明四参数系统和常值大阻尼被动系统在共振频率处具有相似的振动抑制效果,即低频大阻尼特性,与图6中共振频率处各系统的传递率特性相对应。 图7 7 Hz正弦信号激励时域响应 100 Hz正弦信号激励时域响应如图8所示。图8(a)为在高频处,100 Hz正弦信号激励下的时域响应;图8(b)为高频处时域响应的放大图。从图8可知,当输入信号幅值为±1.00 mm时,四参数系统和常值小阻尼被动系统的时域幅值为±0.005 mm,常值大阻尼被动系统的时域幅值在±0.010~±0.015 mm。四参数系统和常值小阻尼被动系统在高频处具有相似的振动抑制效果,即高频小阻尼特性,与图6中高频处各系统的传递率特性相对应。 图8 100 Hz正弦信号激励时域响应 将各系统的时域响应数据根据图7和图8列于表2中。当激励频率为7.00 Hz时,相比于输入信号±1.00 mm,常值小阻尼被动系统、常值大阻尼被动系统和四参数系统的时域幅值分别放大了50倍、1.30倍和1.26倍;相对于常值小阻尼被动系统,四参数系统和常值大阻尼系统在共振频率处具有大阻尼效果。当激励频率为100.00 Hz时,相比于输入信号±1.00 mm,常值小阻尼被动系统、常值大阻尼被动系统和四参数系统的时域幅值分别缩小了200倍、71.43倍和200倍;相对于常值大阻尼被动系统,四参数系统和常值小阻尼系统在高频处具有小阻尼效果。因此,四参数系统能同时保证共振频率和高频处的低时域响应,具有低频大阻尼、高频小阻尼的特性。 表2 不同系统的时域响应 为了验证四参数系统理论计算模型的准确性,根据运动方程式(1)和式(2),在MATLAB/Simulink中搭建仿真环境如图9所示。仿真参数设置如表3所示。采用扫频信号进行信号激励,使用频谱分析仪观察系统输出位移信号及传递率特性。理论计算结果与仿真结果的对比如图10所示。 图9 Simulink仿真 表3 仿真参数设置 图10 理论计算与仿真对比 由图10可知,当频率为7.00 Hz时,常值大阻尼被动系统和四参数系统的计算结果分别为4.04 dB和5.15 dB,仿真结果分别为4.05 dB和5.16 dB,误差分别为0.01 dB和0.01 dB;当频率为100.00 Hz时,常值大阻尼被动系统和四参数系统的计算结果分别为-24.97 dB和-45.34 dB,仿真结果分别为-24.94 dB和-45.43 dB,误差分别为0.03 dB和-0.09 dB。因此,四参数系统的仿真结果与理论计算结果基本吻合一致,验证了理论计算模型的准确性,表明了四参数系统具有频变阻尼特性。 (1)定义了频变阻尼特性,即低频大阻尼、高频小阻尼的系统特性;通过归一化参数,建立了四参数隔振系统的传递率模型,得到了系统等效阻尼,将系统物理参数转换为无量纲参数,更易于分析四参数系统的性能。 (2)提出了一种基于四参数系统参数优化的思路,通过给定不同的初始条件ζ0和ω0,可以得到对应参数N和P的较优取值范围。N和P的取值并非越大越好,均存在临界点,临界点之下越大系统性能越好,临界点之上继续增大会使系统性能变差。基于这个思路,为设计不同指标要求的微振动隔振器以及多参数隔振系统的参数优化提供基础。 (3)从频域和时域上对四参数系统进行性能分析;结果表明,四参数系统能够较好地解决被动系统高低频隔振性能之间的矛盾。利用MATLAB/Simulink对理论计算模型进行了模拟仿真验证,仿真结果与理论计算基本一致。相较于被动隔振系统,四参数系统能够将7 Hz固有频率处的传递率幅值降低28.85 dB,证明低频大阻尼效果显著;同时,采用100 Hz单频正弦信号激励时,时域幅值从±1.00 mm衰减至±0.005 mm,衰减率达99.5%,证明高频小阻尼作用凸显,从而验证了四参数系统的频变阻尼特性,即低共振峰值和良好的高频隔振性能。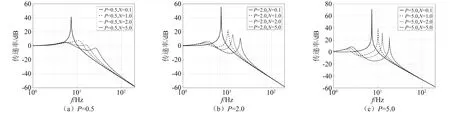
2.2 情况2:N不变,P增大
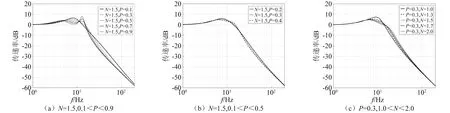
2.3 情况3:N=1.5,P=0.3时,ζ0增大
3 性能分析和模型验证
3.1 频域和时域性能仿真分析


3.2 模型验证
4 结 论

