基于混合基线的任意平面阵列干涉仪测向方法

潘玉剑 宋慧娜

①(杭州电子科技大学电子信息学院 杭州 310018)

②(杭州电子科技大学通信工程学院 杭州 310018)

1 引言

阵列测向是阵列信号处理的一个重要分支，广泛应用于通信、雷达、导引头和声呐等民用和军用领域[1-3]。用于实现测向的阵列有多种结构可供选择。一般较受欢迎的有均匀线阵或均匀圆阵，前者可以采用快速测向算法，后者除了可以方便算法选择还可以留出阵面空间以安装其他传感装置。但在某些情况下，由于其他传感装置的安装需要，或者其他可活动部件引起的机械干涉，阵列结构的规则性将无法被满足，从而导致只能采用非规则阵列。为了应对该实际问题，有必要研究任意的平面阵列结构的测向方法。

在阵列测向算法方面，基于子空间方法或极大似然方法的超分辨算法由于能很好地分辨同频同时多目标而获得较多关注。但对于任意阵列结构，一般不能保证有快速版本的算法可以采用。另外，超分辨算法的超分辨性能以对信号源数的准确估计作为前提。错误的信号源数估计将导致算法性能下降[4]。

相对于超分辨测向算法，在实际应用中更多采用的是相位干涉仪法，即通过比较相位实现测向[5]。虽然干涉仪只能对单目标进行测向，但相对于超分辨算法，其实现简单且精度高。在干涉仪测向中，首要解决的是相位解模糊。对于线阵，常用的解模糊方法有长短基线法[6,7]、虚拟基线法[8]和参差基线法[9,10]等。对于均匀圆阵，以上解模糊方法无法使用。针对该问题，谢立允等人[11]提出了基于等长基线对应的方向函数聚类的解模糊算法，但该算法需要设置聚类门限。王琦[12]在此基础上进行了改进，提出了一种无需聚类门限的解模糊方法，增加了算法的鲁棒性。这两种算法只能基于等长基线进行聚类，无法应用于任意阵列。针对任意平面阵列解模糊，司伟建等人[13,14]提出了立体基线法，通过对最终角度的聚类实现解模糊。但该算法需要额外解一个被称为方位角的镜像模糊，并且出于解镜像模糊的需要，所选基线对的两个基线斜率的正负必须相反，使得其在基线对选择方面缺乏灵活性，不能充分利用阵列基线。

针对任意平面阵的干涉仪测向问题，本文提出了一种称为混合基线的方法。这里的混合基线中的“混合”二字意指对所选基线对中两个基线的长度和斜率没有约束。首先，混合基线算法采用了新的用于聚类分析的改进方向函数。该改进方向函数在原有方向函数的基础上进行了归一化操作，可提高相位解模糊的成功概率。其次，混合基线算法在解相位模糊时，对基线对选择的灵活性非常高。相对于等长基线算法，所选基线对的两个基线可以不等长。相对于立体基线算法，所选基线对的两个基线斜率的正负可以相同。因此可以极大提高用于聚类分析的基线对数量，从而进一步提高相位解模糊的成功概率。最后，本文基于数值仿真方法在随机任意阵上验证了混合基线算法的有效性，并在均匀圆阵和半圆阵上与其他算法进行了解相位模糊的性能比较。

2 任意平面阵信号模型及其干涉测向方法

如图1所示，由编号为1至M的阵元组成的任意阵列位于x-y平面中。阵元位置用极坐标表示。则第m个阵元的位置为(rm,θm)，其中rm表示该阵元到原点的距离，θm表示由x轴逆时针转到该阵元与原点连线的夹角。一来自方向(α,β)的远场信号入射到阵面，其中α ∈[0,2π)表示方位角，β ∈[0,π/2]表示俯仰角。无噪情况下，阵元m输出的快拍t处的基带信号可表示为

图1 任意阵几何示意图

其中，m=1,2,...,M，γm=2πrm/λ，λ为射频信号波长，s[t]为信号包络。

定义阵元之间的连线为基线。任选一根基线，并假设该基线两端分别为阵元m和阵元n，并称其为基线mn。基线mn对应的真实相位差可写为

其中，Arg(·)表示求辐角主值，asin(·)表示求反正弦。

3 任意平面阵干涉仪相位解模糊

根据前面的干涉仪测向方法，要估计来波方向，首先要得到基线相位差。但实际应用中相位差的测量值只能位于(−π,π]范围内，当基线较长时，相位差的真实值会超出该范围而发生以2 π为周期的翻转，此时测量得到的相位差是存在模糊的。由于任意阵的基线长度不受控制，因此解相位模糊是任意阵干涉仪测向最关键的步骤。

根据第2节可知，从阵列中取两根基线构成一个基线对就可以进行测向。对于基线mn和基线pq构成的基线对(mn,pq)，假设其测量相位差分别为φˆmn和φˆpq，可得其与真实相位差的关系为

其中，kmn与kpq为整数，称为相位模糊数。解基线的相位模糊等价于求解其相位模糊数。由式(9)可知，对于任意基线对，只要选择了正确的相位模糊数，就能生成一个只和真实来波方向有关的方向函数。本文的解模糊方法也是基于这一思想。从阵列中可以取出多个基线对，对每个基线对的相位差枚举多个可能的相位模糊数，从而每个基线对可生成多个方向函数。根据式(9)，所有基线对都存在一个共同的对应于真实波达方向的方向函数。因此，在有噪情形下，可通过方向函数聚类来实现相位解模糊。

3.1 聚类方向函数的改进

对于式(9)中的方向函数，可在坐标系中对其进行式(12)分解

而在坐标系中，准确描述信号来波方向应该用

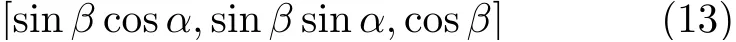
可见，如果对方向函数f进行聚类，则没有充分提取特征，或者等效默认所有枚举的相位模糊数对应的来波方向在单位球上截断点的z坐标都相同，而这是不符合一般实际情况的。因此，基于式(9)中方向函数f的聚类分析将会降低相位解模糊的成功率。为了解决该问题，可将f对z坐标cosβ进行归一化，得到改进方向函数f′

3.2 基线对的选取

由式(18)和式(19)可知，不管是为了减小测向的误差还是为了提高改进方向函数的估计精度从而提高解模糊概率，都希望 dυ和dµ尽可能小。根据式(8)，可将dυ和dµ分别写为

① 尽量选用电长度较长的基线；

② 尽量避免选择夹角过大或过小的基线对。

其中第1个原则是为了减小式(20)中分子对误差的贡献，第2个原则是为了减小式(20)中分母对误差的贡献。

另外，为了提高基于聚类分析解模糊的成功概率，一般希望用于聚类分析的基线对越多越好。这是由于聚类数据越多，越容易从中找到聚类簇。本文所提的方法对基线选择的灵活度很高，所选基线对的基线可共端点，也可不共端点，对基线长度和斜率也没有限制。为了最大限度利用基线，下面给出基于本文方法的任意平面阵的理论最大可用基线对数。

可用的基线包括共端点基线对和不共端点基线对。对于共端点基线对，需要从M元阵列中选出3个阵元。假设所选3个阵元编号为m,n,p，如果考虑基线方向和顺序，最多可构成24个基线对。但即使在有噪情况下，这24个基线对生成的无模糊方向函数都相同。因此，对于每3个阵元，只能选出1个有效基线对，例如(mn,np)。对于不共端点基线，需要从元阵列中选出4个阵元。假设所选4个阵元编号为m,n,p,q，只能选出3个有效的不共端点基线对，例如(mn,pq), (mp,nq)和(mq,np)。这3个基线对生成的无模糊方向函数在有噪情形下是不同的，而其余的基线对都是冗余的。因此对于M元任意阵列，理论最大可用基线对数为+3。后面的数值仿真将对这一理论最大可用基线对数进行验证。

所以，对于本文相位解模糊方法的基线对选取，首先按最大可用基线对数选出所有有效基线对，然后根据原则(a)和原则(b)进行删减。

4 算法步骤

本文所提的基于混合基线的任意平面阵列干涉仪测向方法的步骤如下：

步骤1 从M元任意阵中选取L个基线对，根据测向指标要求的视场角范围假设目标可能的最大俯仰角为βmax，根据测向指标要求的工作带宽假设可能的最小波长λmin，并计算每个基线的模糊数范围。例如对基线mn，其模糊数范围为[−Kmn,Kmn]，其中，Kmn根据式(4)和式(11)，可计算为

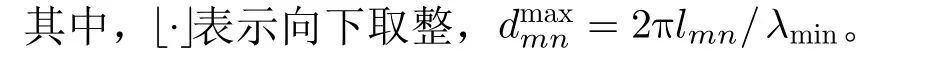
步骤2 以模糊数范围为界，分别对每个基线对的测量相位差按式(11)、式(7)、式(8)和式(9)生成由多个方向函数f构成的方向函数组。如对基线对(mn,pq)，其方向函数组将包含(2Kmn+1)(2Kpq+1)个数值。然后删除每组中绝对值大于 1的方向函数，并将剩余的按式(14)转换为改进方向函数f′。

步骤3 对生成的L个改进方向函数组进行聚类分析，目的是从每组中挑选一个数值，使挑选出的L个数值最接近。聚类分析可采用文献[12,15]中的方法，也可使用文献[16]中介绍的查表法。利用查表法可通过相位测量值查表获得相位模糊数，可大幅缩短计算时间。

步骤4 根据式(15)，基于聚类分析得到的无模糊的改进方向函数计算来波方向(α,β)。由式(18)可知，不同基线对应不同的测向精度，因此存在最优基线的选取问题。由于篇幅所限，这里不作进一步论述，具体内容可参阅文献[15]。

5 数值仿真

为了验证算法的性能，我们对算法进行数值仿真实验。由于已经默认采用干涉仪体制的测向方法，则只要能成功解模糊，得到基线对的无模糊相位差估计值，不同算法间的测向精度没有差别。因此，这里的数值仿真在比较不同算法性能时只进行最关键的解模糊概率的比较。假设所有实验中测向指标要求的最大俯仰角βmax=60°，最小波长λmin=rmax/4，rmax为阵列中阵元到坐标原点的最大距离。阵列输出的采样快拍数T=128，基线的测量相位差通过快速傅里叶变换(Fast Fourier Transformation, FFT)方法获得，如无特别说明，所有实验结果均基于500次蒙特卡罗试验。

(1) 随机任意阵列

首先，仿真算法在一个M=4元随机任意阵列上的测向性能。4 个阵元分别在以直角坐标(0.5λ,1.1λ), (−0.9λ,0.8λ), (−1.1λ, −0.9λ),(1.1λ, −1.1λ)为圆心，以0.01λ为半径的圆内随机均匀分布，阵元编号以第1象限为1按逆时针方向递增。按3.2节可知理论最大可用基线对数为C34+3C44=7。对应地，选择基线对(12,43), (14,23) , (13,24),(12,23) , (23,34) , (34,41) , (41,12)，并命名为BP1到BP7。目标来波方向设置为(45°,20°)，信号信噪比设置为5 dB。最终的角度输出由基线对(13,24)解模糊后的相位差计算得到。

根据式(18)，为了去除测向结果与来波方向的相关性(β=0°时，α的估计误差将为无穷大)，测向结果分别取来波方向在x-x和y-z平面的投影与z轴的夹角，这种表示方法常用于制导和导航应用。这两个投影夹角可分别表示为atan(tanβˆ cosαˆ)和atan(tanβˆ sinαˆ)，其中( ˆ·)表示估计值。根据该公式，真实的投影夹角为14.4°和14.4°。其500次蒙特卡洛仿真的估计结果如图2(a)所示，图中虚线的交叉点为真实角度，小十字表示的测向结果由基线(13,24)解模糊后的改进方向函数得到。由该图可知，所提算法在该4元随机任意阵上可以正确测向。图2(b)为某次蒙特卡洛仿真中7个基线对的所有方向函数，虚线圆为单位圆。图中可见一个包含7个基线对方向函数的聚类簇，该簇中的方向函数各不相同，可见7个基线对均为有效基线对。

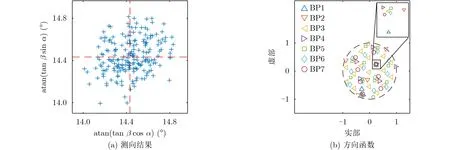
图2 随机任意阵测向性能

(2) 8元均匀圆阵

其次，仿真算法在8元均匀圆阵上的性能，并与文献[12,15]中的不归一化方向函数的等长基线算法作对比。8元圆阵半径设为2.5λ，阵元1位于x轴，其余阵元编号按逆时针方向递增。来波方向与之前相同。对于等长基线法，设置两种基线选择方法，分别为等长基线a和等长基线b。等长基线a 包括基线对(41,52) , (52,63), (63,74) , (74,85),(61,85) , (61,72) , (72,83) , (41,83)。等长基线b包括基线对(31,42) , (42,53) , (53,64), (64,75) , (75,86),(86,17), (17,28) , (28,31)。等长基线a中的基线长于等长基线b中的基线。对于本文的混合基线算法，除去由平行基线构成的基线对(平行基线对夹角为零)，共可提取L=C38+3C48−36=230个基线对。对等长基线和混合基线，都分别考虑方向函数归一化和不归一化的情形。由于干涉仪测向中最关键的是解相位模糊，因此接下来的实验将重点关注各算法对相位的成功解模糊概率。对某基线对成功解模糊定义为对基线对的两个相位模糊数的估计值与其两个测量相位差对应的真实相位模糊数相同。设置信噪比从-14 dB扫描至-2 dB，仿真结果如图3和图4所示。其中图3比较的是各算法对基线对(41,52)的解模糊概率，图4比较的是各算法对基线对(31,42)的解模糊概率。

由图3和图4可知，无论是对于等长基线还是混合基线，经过归一化改进后的方向函数都能提高相位的成功解模糊概率。其次，无论是使用归一化改进方向函数还是不使用归一化改进方向函数，混合基线的成功解模糊概率都高于等长基线，这是由于混合基线在聚类分析解模糊时使用了更多的基线对。另外还可发现，采用了归一化改进方向函数的混合基线拥有最高的相位解模糊性能。

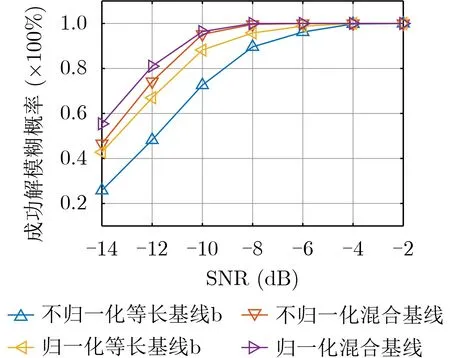
图3 8元阵基线对(41,52)不同信噪比相位解模糊性能比较

图4 8元阵基线对(31,42)不同信噪比相位解模糊性能比较

(3) 5元半圆阵

然后，仿真算法在文献中[13]使用的5元半圆阵上的性能，并与文献[13]中的立体基线算法作对比，阵列结构如图5所示。这里，混合基线除了使用文献[13]中立体基线所用的基线对，即基线对(53,54), (42,23), (43,14)，还额外使用基线对(24,53),(45,32) , (12,43) , (51,43)。这些额外使用的基线对由于其包含的两个基线斜率的正负相同，因而无法被立体基线算法使用。

图5 5元半圆阵示意图

设置信号信噪比为-8dB，来波方位角α=45°。首先将俯仰角β从0°扫描至4 0°，对基线对(53,54)的成功解模糊概率的比较结果见图6。然后，固定信号俯仰角β=20°，变化信号波长λ使半径波长比r/λ从0.5扫描至4，对基线对(53,54)的成功解模糊概率的比较结果见图7。图6和图7显示的算法解模糊性能的比较结果类似。混合基线由于引入了更多的基线对用于解模糊的聚类分析，因而在两个场景下都具有更高的成功解模糊概率。

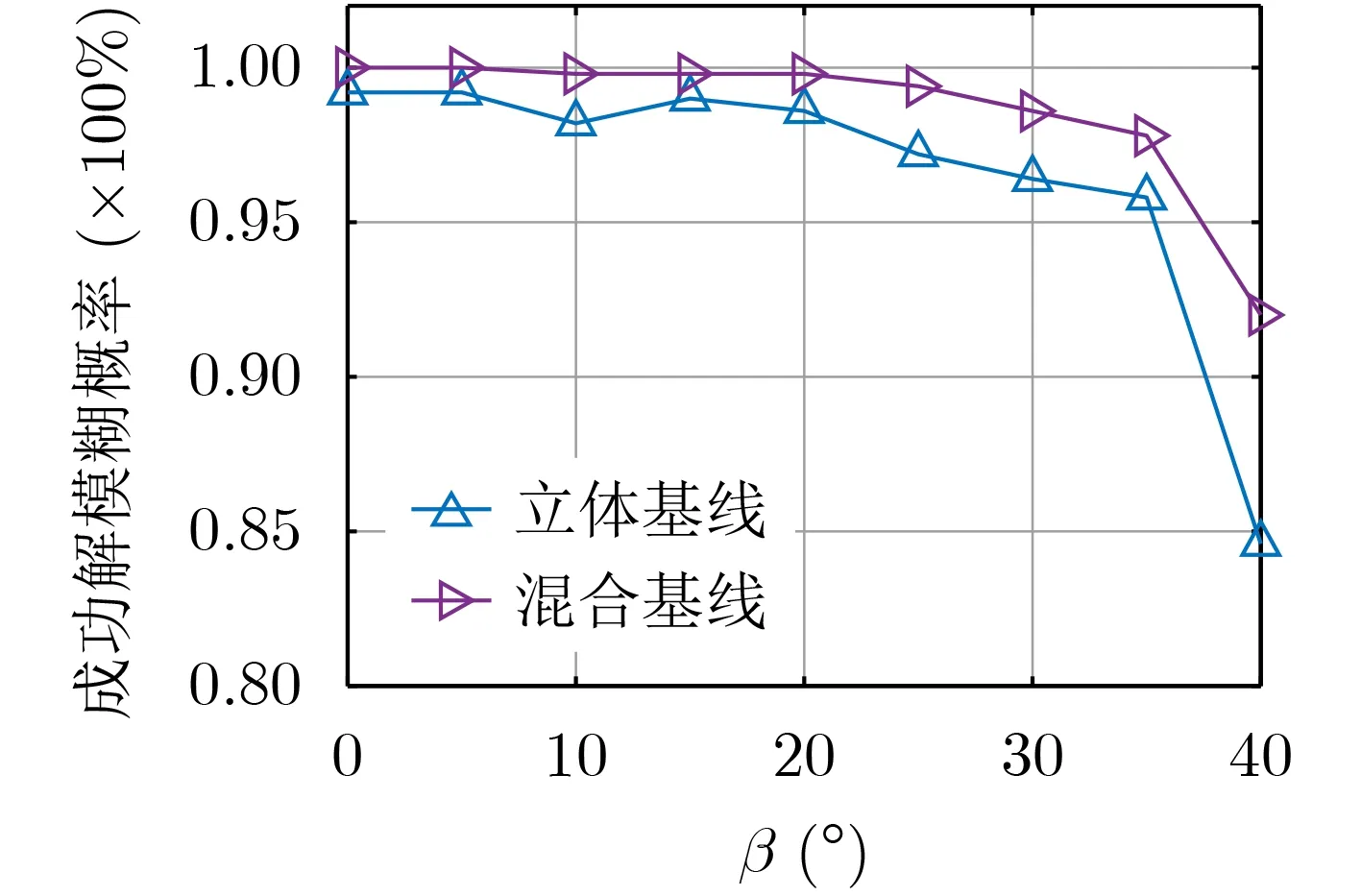
图6 5元半圆阵基线对(53,54)不同俯仰角相位解模糊性能比较

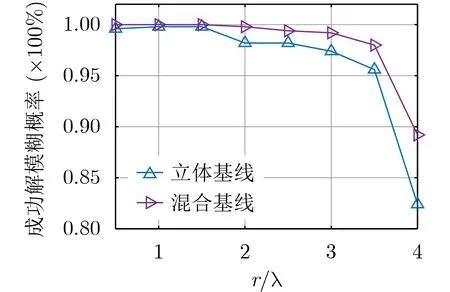
图7 5元半圆阵基线对(53,54)不同波长相位解模糊性能比较

(4) 相同孔径不同阵型

最后，将所提算法应用在相同孔径的不同阵型上，比较解模糊概率的差异。设定用于比较的阵型皆为均匀圆阵。由于4元均匀圆阵和6元均匀圆阵易存在多解性[17]，实际应用中一般使用5元均匀圆阵、7元均匀圆阵和8元均匀圆阵。因此这里只仿真上述3种阵型。设定孔径半径为2.5λ，所有阵型的阵元1位于x轴，其余阵元编号按逆时针方向递增。设置信噪比为-15 dB, -10 dB和-5 dB 3种情形，其他参数与前面相同，仿真结果如表1所示。5元均匀圆阵、7元均匀圆阵和8元均匀圆阵解模糊采用的基线对数量分别为20, 119和230。对于5元均匀圆阵，表中给出的是对基线对(41,53)的解模糊概率，对于7元均匀圆阵和8元均匀圆阵，表中给出的是对基线对(51,73)的解模糊概率。从表中可知，所提算法有着很高的解模糊概率，在信噪比为-10 dB时，3种阵型都可100%解模糊。另外，在信噪比为-15 dB时，随着阵元数的增大，可用于解模糊的基线对数量增大，进而能增大解模糊概率。

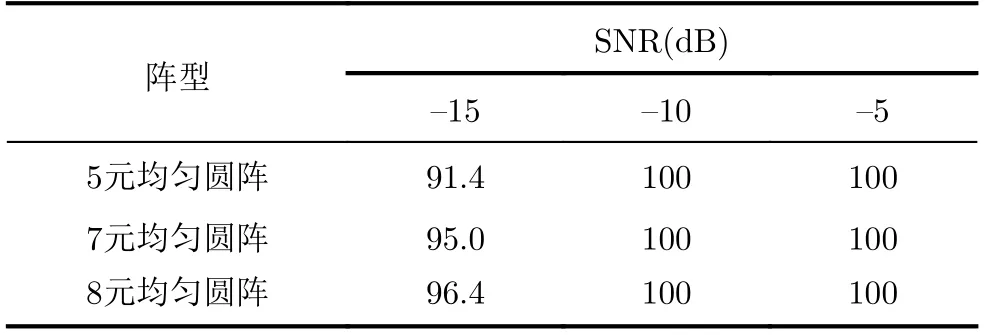
表1 相同孔径不同阵型相位解模糊性能比较(%)

6 结论

本文提出了一种用于任意平面阵列干涉仪测向的混合基线算法。首先，混合基线算法采用了新的用于聚类分析的改进方向函数。该改进方向函数在原有方向函数的基础上进行了归一化操作，可提高成功解模糊概率。其次，混合基线算法在解相位模糊时，对基线对的选择灵活性非常高。相对于等长基线算法，所选基线对的两个基线可以不等长。相对于立体基线算法，所选基线对的两个基线斜率的正负可以相同。因此可以极大提高用于聚类分析的基线对数量，从而进一步提高成功解模糊概率。最后，数值仿真结果显示混合基线算法可处理任意平面阵干涉仪测向问题，并且在均匀圆阵和半圆阵上的解模糊性能均优于现有其他算法。