为螺母设计指南补缺初探——六角螺母外形尺寸设计

孟武功， 蒋杨英

（舟山市7412 工厂研究院， 浙江舟山316041）

0 引言

ISO/TR 16224[1]、GB/Z 32564—2016[2]和VDI 2230[12]是螺母设计的现行指导资料。 但是资料中也仅规定了对边宽度系数S/d≥1.4 的情况， 对于对边小于标准宽度的螺母或螺母与螺栓强度差距较大的情况下， 未给出明确的设计指导。《螺纹联接的理论与计算》[6]中仅用标准对边宽度计算，《螺纹紧固件联接工程》[4]仅提出对螺母体作为“厚壁筒”来计算其内表面切应力。 对于受力较为复杂的螺母体，用简单的方法仅对某些特殊情况下的计算有用，对于更为普遍意义上的内螺纹件设计显然是不完整的。

利用FEM 方法对螺母的载荷与对边的关系进行分析可看到轴向载荷F∝对边宽度S，在有些情况下也会出现高度方向的塌陷（压溃）。 现实是无法预测六角面上或是螺纹牙以外部分的应力， 应用现有资料中介绍的方法得出的计算结果与实际情况存在较大差异。

除非标六角螺母、法兰螺母螺纹的强度问题以外，还有薄壁内螺纹件见图4， 它的承载能力、箱体件上内螺纹的壁厚、冲压件上的内螺纹承载能力、以及预埋螺纹件的安全性预测常常是设计人员重点关注的非标设计问题。

1 旋合长度设计

1.1 设计方法

《紧固件连接设计手册》[7]（见图1）给出了内螺纹剪切强度计算公式：

图1 螺纹牙展开模型

式中：τ—螺纹紧固件联接工程，τ=X×Rmn；Rmn内螺纹抗拉强度；X—剪切强度/抗拉强度比；Fm—极限拉力载荷；D—内螺纹公称直径；b—螺纹牙根宽度， 普通螺纹b=0.87P；kz—考虑各圈螺纹牙受力不均的系数，内、外螺纹不同材料对应的取值如下：

内、外螺纹均为钢：

根据VDI 2230 可查出表1 中数据：

表1 剪切强度与抗拉强度的比例系数

根据VDI 2230 不同性能等级的螺栓与螺母对应的meff/d 关系。 结合表1 中的数据，可将10.9 级螺栓连接副对应的螺母最小有效高度meffmin转化为一个参数方程。

meffmin=d×（0.72264+6.17938×0.99163Rmn

《紧固件联接工程》[4]、VDI 2230[12]、《螺纹连接的理论与计算》[6]、《螺纹联接设计与计算》[13]，分别提出了不同的算法，但计算结果均在meff与meffmin范围中，其中《螺母设计指南》中列出的蒙特卡罗（Monte Carlo）模拟法计算最为简单。

借助CAE 分析不同的高度与应力的关系，结果表明螺母高度对于螺纹部分应力的影响并不比对边大小对应力影响更敏感。 图2 中曲线为提取CAE 分析中螺母外部各节点应力值，揭示了螺母对边宽度、高度与应力之间的关系。

图2 同规格同强度旋合长度由12～16 时的外部应力状态

1.2 螺母高度（或内螺纹深度）计算

前面介绍了有效旋合长度meff的计算方法。通常螺栓的旋入端和内螺纹入口处均有倒角，所以在设计螺母高度（或内螺纹深度）时需考虑端面倒角的高度。 《螺母设计指南》[1-2]中对于倒角的排除采用的是0.6hc，《螺纹连接的理论与计算》[6]采用减去0.5hc，此处选用与《螺母设计指南》一致。

则双面倒角螺母公称高度：

式中：hc—端面倒角高度。

2 螺母对边尺寸设计

注意力都放在螺纹牙形上的受力与分析， 而螺母的支承面、六角对边的应力很少关注。在性能测试中也仅有一个扩孔试验与对边有间接关系， 其他的标准或设计资料基本未涉及。 但在紧固连接中经常会出现支承面刮伤、变形、开裂等问题，也有像图4 中机体上的内螺纹经常会出现开裂或滑牙，但是如何计算？ 设计准则是什么？

图4 机体或箱体上的螺纹孔结构

本文尝试寻找一种比较方便的设计方法。

图3 螺纹上的受力与分解

2.1 螺母设计指南方法计算

首先采用《螺母设计指南》里的螺母脱扣载荷可推导出S 与D 的关系式。

可以看出，此关系式是一个间接结果，由式（11）求得的螺母对边尺寸与我们工程所需要的结果相差较大，或者说，《螺母设计指南》 中所给参数反过来计算就会过于保守。 对设计者来说，需要相对准确的结果。

2.2 数学模型

螺母体的受力比较复杂， 我们试图通过应力计算找到一种解析方法。

2.2.1 切应力

我们可以先把螺母简化为一个厚壁圆筒， 螺纹的径向分力类似于厚壁圆筒受内压力的应力计算[5]，公式为：

式中：α—螺纹的牙形半角；S—螺母对边宽度；d—螺栓公称直径；μth—螺纹摩擦系数；Mn—螺母高度；Fmn—螺母在给定性能下的保证载荷

2.2.2 螺旋升角引起的切向应力

2.2.3 轴向均匀载荷引起的应力

2.3 解析表达式

综合上文提到的三向应力， 就可以通过应力间的相互关系找到所需要的设计方法。

利用目前的已有资料设计非标六角螺母较困难，本文探索一种新方法， 通过三向应力之间的应力关系分析螺母受力，从而实现设计非标六角螺母的目的。

对于三向应力的关系，可采用密塞斯（Von Mises）或特雷斯卡（Tresca）屈服条件进行分析，下面我们根据密塞斯屈服条件：

σ 值以螺母材料在给定条件下的屈服强度代入，则可解得四个结果，即两个复数值，两个实数值，两个实数值中取大的正值即对边尺寸，此处为螺母接触面处。

为清晰观察解的范围，可借助Matlab 进行“数值”运算， 并绘制图5， 观察图5 得到在螺母高度1.2mm 处可得，有±10.7921 解。

图5 函数图解法

函数法与图解法结合，在图形上可印证S 解的范围。

3 模型的应用

3.1 使用方法之一：解析算法

观察图2 及图6 可发现，螺母应力在高度方向上，由上而下逐渐提高，式（16）是一个平均应力方法，所以需要对载荷分布进行必要的修正。

图6 M8、M10、M12 三种规格螺母在不同材料强度下的旋合长度与对边值

分析螺母轴力分布的理论很多，此处借用《螺纹连接的理论与计算》[6]的分布理论。 略去相关的理论推导。

式中：vb、vn、Eb、En分别为螺栓和螺母材料的泊松比和弹性模量。 An、Ab分别为螺母和螺栓的应力面积。

这里螺母的破坏准则，采用屈服强度，即以Rsn替换σ。

分别将计算所需的螺栓与螺母的尺寸代入式 （17）～式（19），再将式（21）代入式（16）的常数项，得到表2 中10级螺母对边最小尺寸。

表2 10.9 螺栓配不同材料性能下的内螺纹的对边S 或外径尺寸与有效旋合长度

（续表2）

若将这些参数与螺母的材料性能相关联， 然后用数学工具把它绘制成曲线。 观察螺母的旋合长度的线型与螺母的载荷分布曲线非常相似，这并非巧合，而是揭示了它们之间的关联关系。

3.2 使用方法之二：数值解

设螺母性能为Rsn，d 是已知的螺纹规格，meff是此前的计算结果，其中仅一个对边尺寸S 为未知数。我们可以用解析计算，但计算模型经过了简化，同时计算期间需人工干预，且过程中间的一些特定的条件需确认，所以并非最优结果。

现有条件下的计算工具十分丰富，可以采用python、VB、VBA、VC 或Matlab 等工具， 借用它们进行非线方程组的数值解，可缩短计算时间并提高计算精度。计算时仅需根据自己对计算精度需求设置即可。 这里仅以python为例： 直接应用密塞斯屈服条件， 此处设置计算精度为0.01。

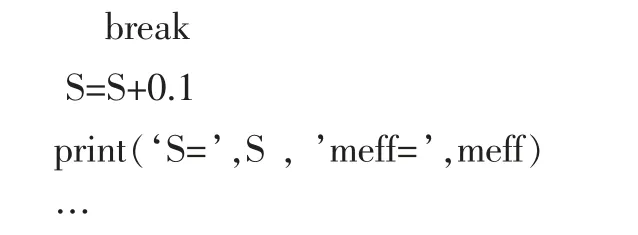
若精度不够可将条件改为0.0001，其他无需干预；当然，可以引入“拟蒙特卡罗”方法，由于我们的未知条件并不多，而且趋势及范围基本明确，所以，即使循环次数不足及时加以调整即可。

通过上面的数值解法稍加改造， 在外面再加一层对不同材料的条件循环， 即可得到符合不同材料要求的对边尺寸S。 下表就用此得到。

4 实例

下面我们将通过三个实例来验证表2 中所设计尺寸数据的准确性。

例1：螺母规格M8×1.25，保证载荷Fm=40kN、配用螺栓刚性，螺母抗拉强度=240MPa，螺母外径D=16.3、高度分别按照m=8～16 进行FEM 分析计算。 提取外层节点应力并绘制曲线。

图7 中有一个明显的趋势，高度大于11 之后应力在高度方向上逐步变平缓，在高度大于16 之后对应力的影响变的无关紧要了。 表2 中的涂色处的高度就在上图的中间部位。

图7 相同材料、相同直径、相同载荷，不同高度尺寸的应力云图

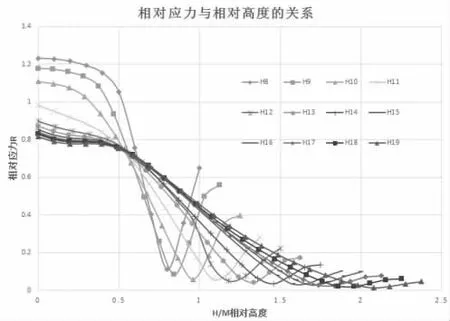
图8 相同直径、不同厚度的螺母，在保证载荷下的外部应力曲线

例2：下面以高度m=8 外径D=10、11、11.5、12、12.5、13、13.5、14.5、15.5，性能800MPa 进行FEM 分析计算，分析其应力分布。 规格参见表2 中800MPa 一栏中参数。

图9 中明显地看到在较小的对边尺寸下螺母体下部应力较高且区域较大，随着对边的加大，高应力深红色区随之减小，而且逐步向内部的左下角集中。上部的低应力蓝色区也逐步扩大。 由图中可明显地看到前两个图的下部有较大的变形且第一个D=10 加载时因变形过大失败。与表2 中D=11.5～13 是符合的。

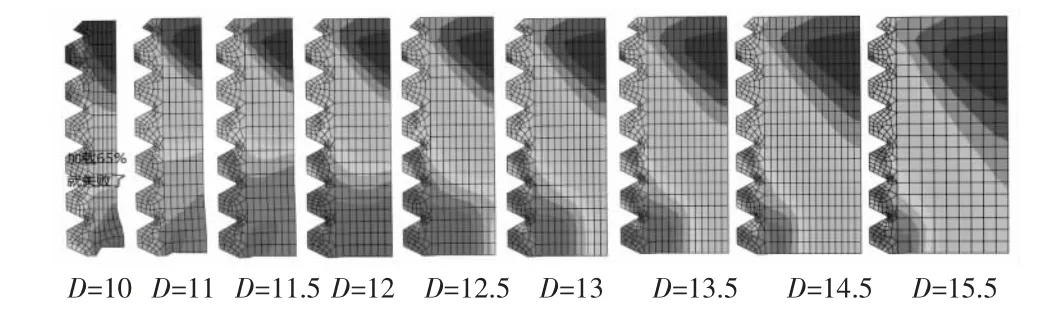
图9 相同高度、相同材料状态，不同的外径或对边尺寸应力云图

图10 可以看出，在S=10 时首先是在45%高度以下应力达到极限应力，之后下降很快，当S≥11.5 应力变化就会变的平稳， 当S大于12 就已很平缓， 在S 加大后逐步趋于平直。 当达到公称S 值最危险部位的应力也只有螺母性能极限的50%左右。

图10 相同高度、不同外径或对边尺寸的应力分布曲线

例3：用三维模型进行仿真，载荷40kN，规格M8 高度18 外径16.6、17、17.6、18.5、21，材料：铝合金，性能240MPa。

可以看到图11 中随着螺母壁厚的增加，应力的分布红色区逐步缩小且向内径的左下角集中， 上部的低应力蓝色区逐步增大。 最小的D=16.6 的一个下部明显有变形，D=17.6 最外部由深红变浅。 这证实了表2 中M8 涂色区的两个S 规格，其基本上是吻合的。

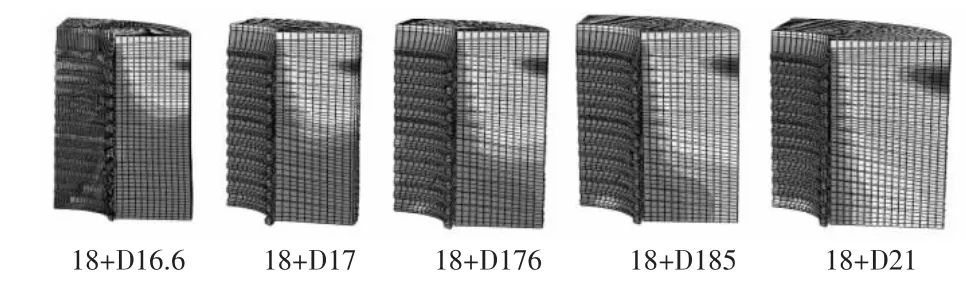
图11 相同高度、同样的材料状态，不同外径或对边尺寸对三维应力分布的影响

5 总结

通过实例我们已验证了部分规格的准确性， 通过表格查询或是通过公式计算要设计螺母的外形尺寸， 或是一些铸件的内螺纹的外部尺寸， 表2 中尺寸是针对简化后的六角螺母而言，如果是六角螺母或是法兰螺母，或是铸件上的内螺纹口缘外有大平面或筋板相助， 表中尺寸会相对更安全一些。

如果说能准确地了解所要设计的内螺纹产品的材料性能， 通过计算或查表就可比较清晰地了解装配后的工作状态下，内螺纹的安全系数。

6 结束语

由于篇幅的原因， 本文仅以较小的视角提出了一些个人对螺母外形尺寸的设计方法， 后续会根据需要在这方面以更大视角展示一些设计方法和验证方法。

随着我国在汽车等各行业的大发展， 在紧固方面会有更多的需求，希望各行业同仁们可以提出自己的看法，或更好的设计理念和方法， 让我们的工业设计尽快地走向世界前列。