同源密码中Montgomery模型的w-坐标研究

陶 铮, 胡 志

1中南大学数学与统计学院 长沙 中国 410083

1 引言

近年来随着量子计算机研究的飞速发展, 以 Shor算法[1]为典型代表的量子算法的具体实现迎来了曙光, 这也预示着目前正使用的公钥密码系统(如RSA 和ECC)将不再安全, 由此将严重危害网络空间中数字通信的机密性和完整性。基于一些在量子计算模型下目前仍是计算困难的问题, 许多新的公钥密码方案被提出, 包括基于格的密码, 基于编码的密码, 基于 Hash 的密码, 基于多变量多项式的密码, 以及基于超奇异椭圆曲线上同源计算的密码,等。公钥密码的研究由此进入了后量子时代。

1.1 基于同源的后量子密码

基于超奇异椭圆曲线同源计算的公钥密码体制由Jao和De Feo在2011年提出[2], 其安全性依赖于寻找两条定义在有限域qF上超奇异椭圆曲线间同源映射的复杂性。目前该问题在量子计算模型下仍是指数时间复杂度的。在美国国家标准与技术研究院(National Institute of Standards and Technology, NIST)启动的后量子密码学标准化计划中, 基于同源的密码方案——超奇异同源密钥封装(Supersingular Isogeny Key Encapsulation,SIKE) 在三轮角逐中均进入公钥加密与密钥建立方案的候选列表[3]。

相对于其他后量子密码, 基于超奇异椭圆曲线同源计算的密码主要有两大优势: (1)由于椭圆曲线具有良好的代数结构, 在相同安全级别条件下, 基于同源的密码具有相对较小的密钥长度; (2)传统ECC已有三十多年的研究历史, 关于 ECC的快速实现和安全防护技术的研究日趋成熟, 故而对于密码系统使用者和实现者而言, 基于同源的密码系统可以更为方便的在未来部署和保护。然而, 同源计算相比ECC中的标量乘法运算而言要复杂得多, 与其他后量子密码相比, 同源密码的实现效率不占优势, 这也极大地影响了其走向实际应用。

1.2 同源密码实现与w-坐标

许多密码学者研究基于超奇异同源密码的高效安全实现, 其中主要运算包括有限域算术、椭圆曲线群律以及同源映射等。有限域算术作为最底层运算适合硬件优化实现[4], 而后两者运算尤其是同源运算较为复杂, 因此优化同源以及群律计算, 是我们所关注的重点[5]。目前超奇异同源密码实现中主要采用Montgomery 曲线模型, 因其可用Montgomery ladder 算法高效安全实现椭圆曲线群律运算[6], 已有关于同源计算的优化工作以及硬件实现也主要集中在该类曲线模型上[7]。

一般的, 椭圆曲线E作为射影直线P的2覆盖, 可诱导从E/ { ± 1 }到P的同构映射, 并由此引出P上的(伪)群律(此时该射影直线称为Kummer线)。对于Montgomery曲线而言,x-坐标诱导了从到P的同构映射, 因此椭圆曲线算术可以只用x-坐标进行, 在简化运算的同时还可以节省带宽。Karati和Sarkar还提出了平方化的Kummer线, 并指出其算术可通过单指令多数据流(Single Instruction Multiple Data, SIMD)指令集加速计算[8]。Hisil和Renes还证明了可以通过加2阶点的方式所构造的同构映射得到新的Kummer 线[9]。

实际上, 在许多应用场景我们并不需要上述诱导映射为同构映射, 从而可考虑一种Kummer 线上x-坐标的推广形式—w-坐标(关于椭圆曲线上有理点坐标的一个有理函数), 来完成椭圆曲线上的群律计算与同源映射计算。自然的, Montgomery 曲线模型上的x-坐标可视为w-坐标的一个特例, 目前已广泛应用于椭圆曲线群律计算和同源计算。Farashahi和Joye针对特征为2的有限域上的Hessian曲线模型给出了w-坐标满足差分加法运算[10]; Farashahi和Hosseini提出了Edwards曲线模型上的w-坐标[11], 其诱导产生的差分加法同样适配Montogomery ladder 算法。Kim等人[12]随后将该w-坐标技术用到了同源计算中, 得到了目前关于一些小的奇数阶同源的最好计算结果。Huang 等人[13]和 Drylo 等人[14]各自独立提出Huff 曲线模型上的w-坐标用于高效群律计算和同源计算。

使用w-坐标来实现椭圆曲线群律计算和同源计算的优点主要有:

(1)w-坐标支持点的差分加法运算(即已知点P, Q, P-Q, 可计算点P+Q), 加法和倍点计算运算效率高。设M, S, a分别表示有限域中的乘法、平方和加法运算。以Montgomery曲线模型为例, 其差分加法/倍点运算仅需4M+2S (若令Z-坐标为1, 则计算代价还可以减少1M)。

(2)w-坐标的差分加法运算可适配Montgomery ladder 算法, 标量乘法计算的每轮迭代计算量一致, 从而可预防侧信道攻击。这里主要针对简单功耗分析攻击 (Simple Power Analysis, SPA)。由于芯片在运行不同的指令时消耗的功率不一样, 若算法迭代每步计算量不一致, 则攻击者可利用高分辨率功率测量仪器从外部测量芯片功率的变化, 进而提取部分或全部密钥以达到攻击的目的。

(3)w-坐标与标准的椭圆曲线有理点 (x,y)-坐标相比, 不仅减少了群律计算和同源计算中的中间计算量(少算一个坐标), 还可以节省一半的带宽。如在ECC中取素数NIST p256的情况下, 可将传递的有理点参数从512 bit节省到256 bit; 在SIKE中取素数为p434的时候, 可将传递的有理点参数从1736 bit减少为868 bit.

当然,w-坐标也存在不足之处: 由于它诱导的椭圆曲线群律运算并不完备, 更多的时候我们将其称为“伪”群律运算。但我们可以通过一些特殊的处理方式弥补这一短处, 从而有效的支持相关计算。

1.3 本文工作

目前已有的关于椭圆曲线上w-坐标的构造根据所选择的曲线模型有所不同。由于Edwards, Huff, Jacobi等曲线模型在某些条件下可与Montgomery曲线模型建立双有理等价映射, 因此若能在Montgomery曲线模型上开发出更多的w-坐标, 则其他曲线模型可得到更多w-坐标的选择, 从而设计更优的算法。

本文基于前述文献工作基础, 提出利用Montgomery曲线上的2-同源构造出3类新的w-坐标。与x-坐标相同的是, 它们均可应用于Montgomery ladder算法。更进一步的, 这类w-坐标技术可用于奇数次同源计算的优化, 包括同源映射的像以及目标同源曲线参数相关计算。

本文结构如下: 第2节主要介绍了本文需要用到的预备知识; 第3节主要介绍了其他曲线模型上已知的w-坐标, 并描述了它们对于同源密码的优化;第4节描述了本文的主要工作, 通过2-同源复合x-坐标得到新的w-坐标; 第5节中我们研究了如何将w-坐标用于同源的计算。

2 预备知识

2.1 Montgomery曲线上的群律

设定义在域qF(特征不为2, 3)上的Montgomery曲线E[6]为

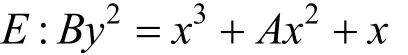
其中参数A和B是域qF上的值, 满 0B≠ ,24A≠ . 若令xXZ= ,yYZ= ,则对应投影模型

无穷远点为 Θ= ( 0:1:0).

结论1.取E上两点则由群律公式[6]可得

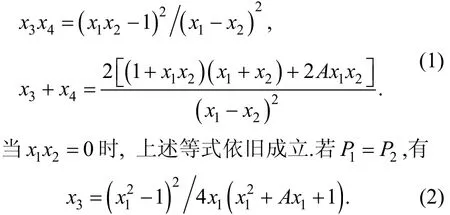
2.2 2-同源的计算

根据Vélu公式[15], 已知同源映射的核, 即得到同源公式与像曲线的系数。不妨设T是E的2阶点, 即T=(0,0),T=(a,0)或其中

定理1. 根据Vélu公式[15]可得, Montgomery曲线E上以2-阶点所生成的子群为核的2-同源公式.

由于1F是Weierstrass型曲线, 于是据1F可构造同构映射 2ψ, 将1F转换成Montgomery曲线.

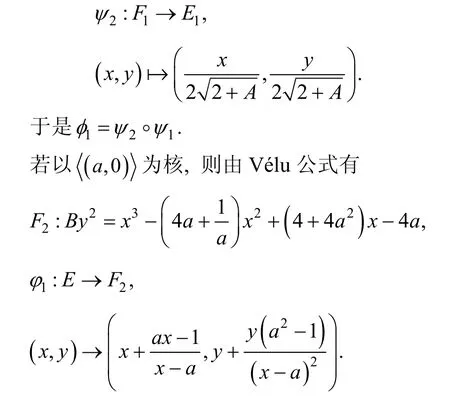
同理, 可构造同构映射将 2F转换成Montgomery曲线模型.

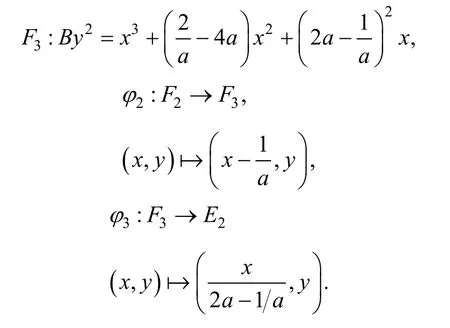
因此φ2=φ3°φ2°φ1.

同理可得以(1a,0)为核的2-同源.

3 椭圆曲线上的w-坐标

如同引言中提到的, Montgomery曲线模型(E,Θ)上的x-坐标诱导了从E/ {± 1 }到射影直线P(即Kummer线,设为)的同构映射, 因此椭圆曲线算术可以只用x-坐标进行, 从而达到简化计算的目的。为了在其他曲线模型上达到和Montgomery曲线上x-坐标类似的群律计算公式, 人们提出了w-坐标可诱导其他曲线模型到射影直线P的双射。目前已知其他曲线上的w-坐标如下所述。

在twisted Edwards曲线模型[11]

其中, Farashahi和Hossei为了优化群律计算同时应用Montgomery ladder算法, 提出了 Edwards曲线模型上的w-坐标[11], 具体如下

令w(x,y) =d(xy)2. 设P,Q∊ETE, 令w1=w(P),w2=w(Q),w3=w(P+Q),w0=w(P-Q),w4=w( [ 2]P). 则有

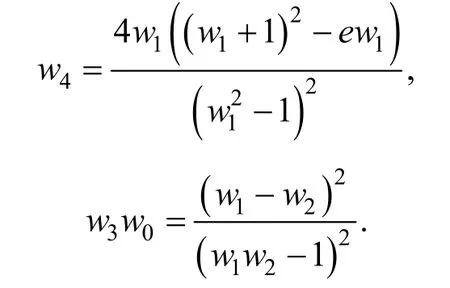
其中e= 4ad. Farashahi 等人利用这种w-坐标将倍-加运算的计算量减少为6M+4S+1D, 其中M,S,D分别表示乘法, 平方和常数乘法。同时他们还提出twisted Edwards曲线模型上另外几种w-坐标

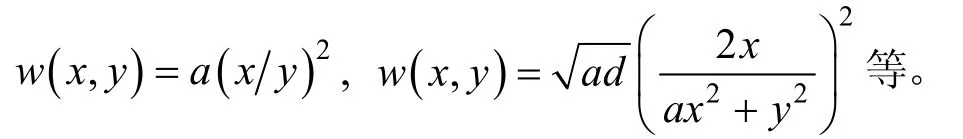
随后Kim 等人[12]将上述结果应用到了Edwards曲线上奇数次同源的计算中, 并验证了奇数次同源的计算中Edwards曲线比Montgomery曲线在实际速度中更加突出, 且在曲线参数的传递上比Montgomery更有优越性。在应用w-坐标之后, CSIDH (基于SIDH的一种变种密码方案)的实现比之前提高了20%.

由于Montgomery和Edwards曲线上的高效群律和同源计算公式, 所以目前大部分关于SIDH的实现中主要选择这两类曲线模型。

Huang 等人[13]在Huff曲线模型

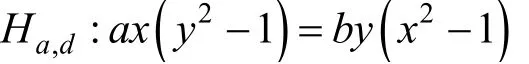
上提出了一类新的w-坐标, 并利用w-坐标优化了Huff曲线上的群律计算, 将倍-加运算量减少为6M+4S+1D, 加快了约40%. 同时在2-同源和奇数次同源的计算中, 利用w-坐标之后运算量减少了约50%, 将 Huff曲线上的运算量减少到了与Montgomery曲线相同。 Drylo等人[14]在Huff曲线上也得到了类似结果。

综上所述, 使用w-坐标可优化不同曲线模型上的群律计算, 对于不同椭圆曲线模型上的w-坐标与普通坐标的倍-加运算量对比结果如下表。

表1 倍-加运算运算量对比Table 1 The Comparison of Computational Costs of Double-and-Add Operation

由于在Montgomery曲线模型上的x-坐标可以作为w-坐标, 所以运算量没有明显的改变。但从上表可以看出, 在其他曲线模型上使用w-坐标可以得到与Montgomery曲线模型类似的群律算法。最后三类曲线上的w-坐标还有待研究。

4 Montgomery曲线上的w-坐标

在同一曲线模型中, 利用Hisil和Renes的方法[16], 我们可以通过加上2阶点平移的方式得到更多的w-坐标。例如在Montgomery曲线模型上可以将x-坐标看成一种w-坐标, 再通过2阶点的加法得到一类新的w-坐标[18]。

设Montgomery曲线模型(E,Θ)上的任意一点P= (x,y),由于w-坐标将(E,Θ)映射到x轴, 即

其中τT是之间的同构映射。例如, 若令.从而通过加T平移得到的w-坐标为w(P)= 1x.

若T= (a,0),同理, 若

本文提出在Montgomey曲线w-坐标上复合2-同源φ, 可以得到新的w-坐标, 即有

其中E′的Kummer线记为间的同态映射。

对于E上2阶点Q生成的子群Q= {Q,Θ}的陪集, 因为w(P+Q)对于差分加法满足平行四边形法则[6], 所以 ( )wPQ+ 仍满足平行四边形法则。 由2-同源φ是同态的, 于是复合可得E上新的w-坐标wwφ′= ° .

5 奇数次同源的计算

可由Montgomery曲线系数与twisted Edwards曲线系数d的关系[24], 求解像曲线系数

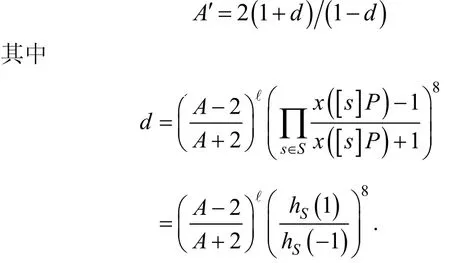
因此可利用SIMD指令集将坐标计算和系数计算并行化处理, 从而得到同源密码实现的进一步加速。注意到公式(13)和(14)计算公式与上述公式在形式上一致, 将上述公式中的w-坐标换成w-坐标同样可得到类似的结果。

6 结论

本文研究了可用于高效安全计算椭圆曲线群律运算和同源映射的w-坐标技术, 通过总结目前在各类椭圆曲线模型(其中重点考查Montgomery模型)上的w-坐标及其相关计算, 分析其特点与带来的计算上的优势。特别的, 我们采用Montgomery曲线模型上的2-同源, 与已知的w-坐标进行复合, 得到三种新的w-坐标, 对它们诱导的群律进行了推导, 最后将其应用到了奇数次同源的计算优化上。而对于其他曲线模型上的w-坐标, 同样可以利用类似技巧进行重新构造, 未来期待能利用新的w-坐标进一步支持或优化同源密码中的计算, 从而推动超奇异同源密码走向实际应用。