基于FPGA的Leighton-Micali签名方案密钥 生成的高速可配置实现

胡 潇, 宋逸峰, 汪文浩, 田 静

南京大学 电子科学与技术工程学院 南京 中国 210023

1 引言

由于量子计算的飞速发展, 现代密码学面临着巨大的挑战。目前常用的传统签名方案, 如RSA[1], DSA[2], ECDSA[3]和EdDSA[4]等算法, 都基于某些数学假设如大整数因式分解困难与计算离散对数的困难。然而, Shor的算法[5]证明, 这类困难在量子计算机上将会被快速解决。而随着量子计算领域快速发展, 学者预测量子计算机将会在不远的将来被设计出来。因此, 可抵御量子计算机攻击的后量子加密方案正在被积极探索, 标准化团队与学术团体也正在对这些方案积极地开展标准化进程。

美国国家标准技术研究所(National Institute of Standards and Technology, NIST)于2016年提出后量子标准方案评审标准和要求[6]后, 向学术界和工业界广泛征集方案。2017年进行第一轮的评审, 在收到的82个方案中选出了69个候选方案[7], 并在2018年召开了第一届PQC的标准化会议[8]。随后进行了更全面更进一步的评估, 于2019年召开了第二届PQC标准化会议, 由第一轮69个候选方案中选出了26个方案进入第二轮[7]。2020年的第三轮评审选出了7个入围方案与8个候补方案[9], 第三届的PQC标准化会议则会在2021年举行, 预计2022年年初NIST将公布标准初稿并公开征求建议[9]。

基于哈希的签名方案(Hash-based Signature, HBS)是后量子加密方案中最有潜力的类别之一[9-10], 其中主要的计算函数是单向哈希函数(Hash)如SHA2[11]和SHA3[12]。相较于其他的后量子加密方案, 如基于格[13]、基于同源[14]、基于编码[15]的加密方案, 基于哈希的加密方案经过充分的研究, 不需要额外的数学假设, 安全性完全依赖于内部哈希函数的安全性[10,16-19], 更易于实现[20], 具有更小的签名尺寸[16], 且在签名和验证的计算效率上也常常优于其他类别[21]。

HBS方案由默克尔树(Merkle Tree)与单次签名(One Time Signature, OTS)构成[22]: OTS方案中, 一个私钥用于一条信息的签名, 对应的公钥用于验证签名的正确性; 而HBS的树为一棵二叉默克尔树(以下简称为二叉树), 其中树的每个叶子节点都是一个OTS公钥的哈希值, 内部节点是用其对应的子节点计算出的哈希值, 树的根节点用于构成HBS的公钥。签名时, HBS的签名由一个OTS的叶子节点与该叶子节点到达根节点的路径节点构成。这些路径节点用于帮助签名的验证。

Leighton-Micali签名(Leighton Micali Signature, LMS)[23]和扩展的默克尔签名方案(eXtended Merkle Signature Scheme, XMSS)[24]是两种目前进入因特尔工程任务组(Internet Engineering Task Force, IETF)标准化进程的高效HBS方案[25]。并于2020年十月份由NIST确定为两种过渡方案标准, 在最终PQC标准确定下来之前针对有抗量子签名需求的应用所使用[16]。这两种方案都是由经典的默克尔算法发展而来的[22], 是目前最新与最成熟的两种HBS方案[16]。与XMSS相比, LMS具有密钥和签名尺寸更小的优势, 这使得该方案在很多场景下具有更多潜力, 特别是传输带宽受限的场景[18]。但是, 在相同的安全等级下, 相对于XMSS, LMS需要进行更多哈希计算。故而对该方案的核心哈希运算进行加速将极大程度有利于该方案的实际应用。且对于LMS方案的三个主要过程: 密钥生成(Key generation)、签名(Signature)和验证(Verification), 密钥生成过程是消耗哈希计算最多的过程, 平均哈希运算次数是后两个过程的两倍[23]。因此, 加速密钥生成过程可以有效提高整个协议的速度。

需要说明的是, 由于LMS方案是一种有状态(Stateful)的HBS方案, 不能使用同一个私钥对不同信息进行多次签名, 否则存在被第三方伪造签名的可能性[23]。同时, 由于LMS的签名中包含由内部节点构成的路径, 需要在签名前结束生成密钥的过程。考虑到HBS方案的主要应用场景是物联网(Internet of Things, IoT)[18,26], 在这些应用场景下, 将会产生大量的签名, 而由于前述的两种特性, 单棵LMS树生成的密钥安全时间有限[23,27]。因此, 加速密钥生成, 对推动LMS方案进入实际应用具有重要意义。同时, 考虑到物联网中资源受限的使用场景, 设计速度与面积之间的折衷方案(如软硬协同系统)也将对推进LMS进入实际应用产生积极影响。

对于LMS相关实现工作, 对于签名和验证的加速与优化工作取得了较多的进展[18,20,28-30]。但是, 对于密钥生成过程, LMS方案作为一种较新提出的后量子签名方案, 目前的工作进展较少: 文献[23]中进行了基于多线程CPU的实现, 给出了同一参数的不同树高的密钥生成; 文献[31]和文献[32]提供了一种基于ARM平台的低功耗LMS实现; 其后, 文献[29]与文献[30]中提出了一种基于CPU的LMS安全启动应用。而对于软硬件协同系统, 目前LMS方案没有对应的相关工作。综上, 基于FPGA的硬件加速器与软硬件协同系统将填补这部分工作的空缺从而对LMS协议的实际应用有较大的推进作用。

本工作中, 我们结合算法特征和架构优化, 首先设计了一种高效的SHA3模块, 并基于此模块提出了基于ZYNQ架构的软硬协同系统。同时, 对于 LMS中最耗时的密钥生成过程, 设计了一种高效且可配置的架构。为了同时获得低延迟与高硬件利用率, 该架构的并行度根据参数集进行设计。仿真与FPGA实现结果显示, 该架构较现有的CPU实现在速度上有55~2091倍的速度提升。

具体的工作总结如下:

· 相较于原有的LMS方案, 选择使用比SHA2哈希函数安全度更高的SHA3哈希函数, 进行了软件验证。并对SHA3实现了适用于LMS方案的架构设计, 以提升哈希模块的硬件利用率。本文中对哈希模块进行了单独的性能评估与比较, 与最新的相关工作相比, 本文中设计的哈希模块具有相当的吞吐率性能。

· 基于SHA3架构, 提出一种基于ZYNQ开发板的软硬协同系统, 其中核心SHA3模块由可编程逻辑实现, 其余操作由CPU实现。该软硬协同系统在占用较少资源的基础上, 支持LMS的整个协议过程, 为IoT场景下资源受限的LMS应用提供了参考。

· 针对LMS方案中耗时最长的密钥生成过程, 设计了一种高速且可配置的专属加速器。该加速器可以容纳LMS原方案中提出的所有参数, 在高并行度与高硬件利用率上取得了最佳的折中。当二叉树深度大幅增加, 只增加非常少的硬件消耗。且本文的架构被设计为在不同参数运行下均可保持功率恒定, 一定程度上可以抵御功率攻击。

· 对于设计的密钥生成架构, 在Xilinx Zynq UltraScale+的开发板上进行了实现, 在使用的硬件资源很少的基础下, 实现了285M赫兹的时钟频率。相较于基于SHA3的源码在CPU上的多线程实现, 本工作实现了2~4个数量级的速度提升。

需要说明的是, 本文中关于全硬件密钥生成架构的初步介绍已发表文献[33], 而本文新的贡献点在于: (1)软硬协同系统的设计; (2)哈希模块的性能评估与比较; (3)对于全硬件密钥生成架构, 新增了公钥生成模块的可停止处理, 和可支持的最大树高阈值分析与讨论。

本文结构如下: 第2节介绍LMS签名方案的主要流程与密钥生成部分的具体算法; 第3节具体介绍核心哈希函数的硬件实现、使用硬件进行哈希计算的软硬协同系统的设计以及LMS签名方案密钥生成部分的全硬件实现设计; 第4节介绍实验过程并对实验结果进行对比与分析; 第5节为总结与展望。

2 LMS签名方案描述

本章节中, 首先简要介绍LMS签名方案的主要流程, 然后介绍目前已有的LMS参数集, 最后详细介绍LMS密钥生成算法以及SHA3哈希算法, 即本工作主要关心的算法。

2.1 LMS方案主要流程

与传统签名方案一致, LMS方案的三个主要过程为: 密钥生成、签名和验证。对于二叉树树高为h的LMS方案, 一次密钥生成产生的密钥可用于签名与验证2h个信息。需要说明的是, 对树高为h的LMS树, 所有节点均有自己的索引值, 范围是1~2h+1–1。对内部节点编号(Node number)规则是, 对于编号N<2h的内部节点, 它的左右子节点的编号分别为2N和2N+1; 对于叶子节点, 叶子编号(Leaf number)依次为2h, 2h+1, …, 2h+2h–1.

密钥生成: 密钥生成阶段, 根据LMS参数类型lms_type确定树高h, 根据OTS类型ots_type确定OTS内部参数。首先, 以0~2h为索引生成2h组OTS密钥对, 其中的私钥用以构成LMS私钥。然后开始构造二叉树以生成LMS公钥: 二叉树的2h个叶子节点中, 每个节点都包括叶子编号以及一个OTS公钥的信息; 内部节点的值T[r]是由其两个子节点的值T[2r]和T[2r+1]连接后再进行哈希计算得到的。二叉树的根节点的值T[1]用以构成LMS的公钥, 此公钥可以验证2h个签名。

签名: 单个OTS的私钥对某个信息产生的签名, 可由对应的OTS公钥进行验证。而在LMS方案中, 单次签名过程中使用某个叶子节点对应的OTS私钥进行签名。产生的LMS签名中, 除了OTS签名, 还包括OTS类型ots_type、叶子节点索引q以及从该叶子节点计算到根节点的路径(Array path)。对于树高为h的二叉树, 该路径包括h个节点的哈希值。如图1所示, 对于层数为3的二叉树中的叶子节点leaf*, 路径包括该叶子节点的兄弟节点leaf1, 通过这两个节点可计算出T[5], 故往下计算需要兄弟节点T[4], 同理, 第三层需要的节点值为T[3]。

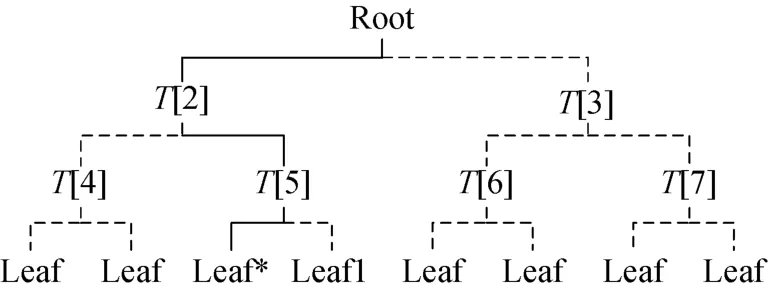
图1 LMS签名中的路径Figure 1 Array path of LMS signature

验证: 对于某个签名, 首先使用其中的OTS签名部分计算出OTS公钥, 再使用此公钥计算出对应的叶子节点值。接着根据签名中的路径计算出根节点。计算出的根节点如果与LMS公钥相符, 则签名有效, 否则无效。

2.2 OTS&LMS参数集

首先, LMS签名协议被提出的同时, 相应的适用参数集也被提出, 包括OTS参数与LMS参数。

表1为OTS方案的参数, LMS中采用Winternitz OTS(WOTS)[34]作为其OTS方案,其中的主要参数为ots_type, H,n,w,p。其中,ots_type为4个字节长的参数类型标识符, 即通过ots_type可知其他OTS参数的值;H指哈希函数的类型, 在本工作中选择高安全度与高灵活性的SHA3_256函数;n指哈希函数输出的字节数, 这个数的选取对整个签名方案的安全性都有较大影响;w是Winternitz系数的位宽, 其选取对安全性几乎没有影响, 它的值描述了签名长度与计算延时的折中: 增加w的大小会减少签名的长度但相应的密钥生成的时间会增加;p是由n和w决定的参数, 同时决定了密钥生成中的哈希计算的迭代次数;sig_len指签名的字节数, 一般来说,sig_len= 4 +n(p+ 1)。

表1 OTS参数集Table 1 Parameter sets of OTS

表2为LMS方案的参数, 主要参数为lms_type,H,m,h。其中,lms_type为4个字节长的参数类型标识符, 即通过lms_type可知其他LMS参数的值;H指哈希函数的类型, 为保证安全性, LMS中哈希函数与LM-OTS中哈希函数应保持一致, 防止攻击者对其中安全性较弱的哈希函数进行攻击[23], 故本工作中实现的哈希函数均为SHA3_256函数, 此后不再赘述;m指LMS树的节点的值的字节长度, 与LMS选取的哈希函数的输出长度一致, 由于H不做区分, 故m与表1中n相等, 均为32, 下文不再做区分;h指LMS的树高。

表2 LMS参数集Table 2 Parameter sets of LMS

2.3 LMS密钥生成

本小节首先介绍LMS算法中核心的哈希函数; 然后介绍WOTS的密钥对生成算法, 最后介绍LMS的密钥对生成算法。此节介绍的算法参考了文献[7]与[23]。

2.3.1 SHA3_256函数

对于哈希函数, 本工作选择比原LMS方案中SHA2函数更新一代的NIST第三代标准哈希函数SHA3函数。为了与文献[23]中安全度一致, 选择输出长度为256比特的SHA3函数即SHA3_256函数。

SHA3_256函数的计算流程图由图2所示, 首先包含一组打包过程(Pad), 此过程是将不定长的数据打包为1088比特整数倍长度的数据方便后续处理, 具体打包规则见文献[7]; 接着将打包后的数据流分别传输到核心函数f中。

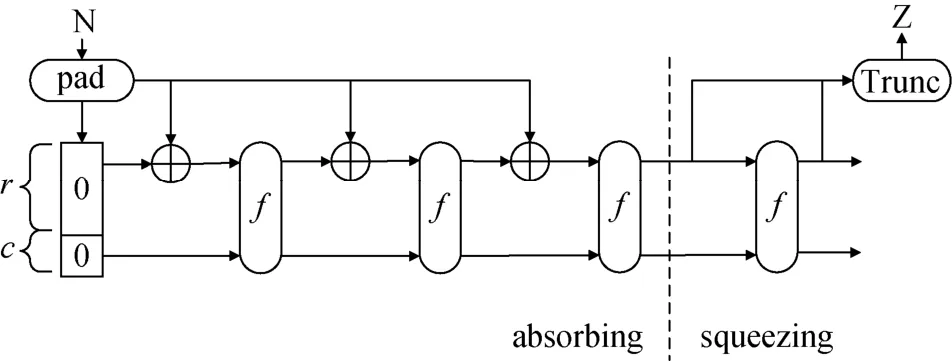
图2 SHA3函数Figure 2 SHA3 function

核心f函数(KECCAK函数)主要由THETA, RHO, PI, CHI, IOTA 5步组成。具体算法细节见算法1, 其中异或XOR(⊕), 取反NOT和按位与AND操作均是位逻辑运算, 旋转ROT是逐位循环移位操作, RC是一个包含24个元素的常数序列。

算法1.SHA3核心函数——KECCAK. 输入: 状态数组A; 输出: 新状态数组A′; 1. FOR 0; 24; 1 DO iiii =﹤=+ 2.( )THETA:0 , 4, 0 25 xyz﹤≤≤≤ 3. [ ] [ ] [ ] [ ],, ,0, ,1, ,2,CxyzAxzAxzAxz =⊕⊕[ ] [ ],3, ,4,AxzAxz ⊕⊕ 4. [ ] ( ) ( ),1, 1,1 DxzCxzROTCx ■ ■■ ■=-⊕ +■ ■■ ■5. [ ] [ ] [ ],, ,, ,AxyzAxyzDxz ′= ⊕6. ( )RHO: 0,4xy≤ ≤7. [ ] [ ][ ](),, ,, , ,AxyzROTAxyzrxy ′=8. ( )PI: 0 , 4,0 25 xyz﹤≤≤≤9. ( ) [ ],2 3 , ,,ByxyzAxyz ■■■■=+10.( )CHI: 0 , 4,0 25 xyz11.[ ] [ ],, ,,AxyzBxyz = ⊕( ) ( )()()()+1,, 2,,NOTBxyzANDBxyz ■ ■■+■ ■■■■

?

2.3.2 OTS密钥对生成算法

OTS密钥对生成算法中包括私钥生成与公钥生成, 以下分别进行介绍。

OTS私钥生成算法如算法2所示: 输入随机值I和seed, 叶子节点索引值q和参数类型ots_type, 输出一个OTS私钥。需要生成序列数为p的x序列。使用初始seed值与参数I,q, 0xff和索引值i进行一次哈希计算, 即可得到一个x[i]。注意此处的0xff是一个1字节长的常数, 索引值i是一个2字节长的无符号数。故一次OTS私钥计算过程将调用p次哈希计算。生成的x序列与I, q和ots_type值组成一个OTS私钥。

?

OTS公钥生成算法如算法3所示: 输入随机值I, 参数类型ots_type, 一个OTS私钥, 输出一个OTS公钥。首先取出私钥中的x序列值, 再对其进行哈希计算。对于每个索引值为i的x[i], 进行2w–1次哈希的迭代计算, 每次计算输入为上一次哈希输出值temp(初始temp=x[i])与I, q, i和迭代数的索引值j的组合值, 第2w–1次哈希的输出值为y[i]。注意此处的索引值i是2字节长的无符号数, 内部循环j是1字节长的无符号数。对于长度为p的x序列, 进行p组迭代, 得到序列长度为p的y序列。将y序列与I,q,D_PBLC=0x8181组合, 再进行一次哈希计算, 得到OTS公钥的主要组成部分K。

?

?

2.3.3 LMS密钥生成算法

LMS密钥算法中包括私钥生成与公钥生成, 以下分别进行介绍。

?

LMS私钥生成算法如算法4所示: 输入参数类型ots_type, 树的深度h, 输出LMS的全部私钥值。seed和I分别是长度为32比特和16比特的初始随机值, 一棵二叉树使用的seed和I在初始化后不再改变;h指LMS二叉树的深度, 对于二叉树深度为h的LMS签名协议, 私钥生成阶段需要生成2h个OTS私钥, 即调用2h次OTS私钥生成算法。q为叶子节点的索引值。

算法5.LMS公钥生成流程. 输入: OTS公钥中的哈希数组K; 输出: LMS公钥 {lms_type||ots_type||I||T[1]}; 1. 1()FOR 2 1; 1; 1 DOh+rrrr = -﹥=-

?

LMS公钥生成算法如算法5所示: 输入2h个OTS公钥值的K, 输出LMS的公钥值。首先, 参数D_LEAF=0x8282, D_INTR=0x8383; 假设对于每个节点的索引值为r, 且对于每个索引值为r的内部节点, 其子节点的索引值为2r和2r+1。对于输入的2h个K, 索引值范围为2h~2h+1。当r>=2h时, 此时计算叶子节点的值, 将该K值与I,r, D_LEAF组合后进行一次哈希计算; 当r<2h时, 此时计算内部节点的值, 将该叶子节点值与其兄弟节点的值组合, 再与I,r,D_INTR组合后进行一次哈希计算, 得到这两个节点的父节点的值。层层计算后, 最终得到的根节点值T[1]。将T[1]与参数类型ots_type, OTS类型ots_type和随机值I组合后, 即构成LMS公钥。该公钥可用于验证2h个签名。

3 本文工作

本文实现了LMS协议的软硬协同系统与针对密钥生成过程的全硬件架构设计。本章首先介绍核心SHA3函数的相关设计, 接着介绍软硬协同系统, 最后介绍密钥生成架构。

3.1 SHA3函数模块设计

哈希函数是整个LMS密钥生成过程中最核心的计算模块, 其算法过程已经在章节2.2.1中详细描述, 在这里介绍几个本工作中实际使用到的模块。

3.1.1 KECCAK模块

SHA3_256中核心的KECCAK模块如图3所示。同算法1, 该模块的主要子模块包括THETA, IOTA,RHO, PI, CHI。主要运算均为逻辑运算, 移位, 逻辑与, 异或等, 子模块中的具体逻辑运算如算法1中所示。KECCAK模块被设计为一次性可最多处理1600比特的输入且在27个时钟周期内完成计算。

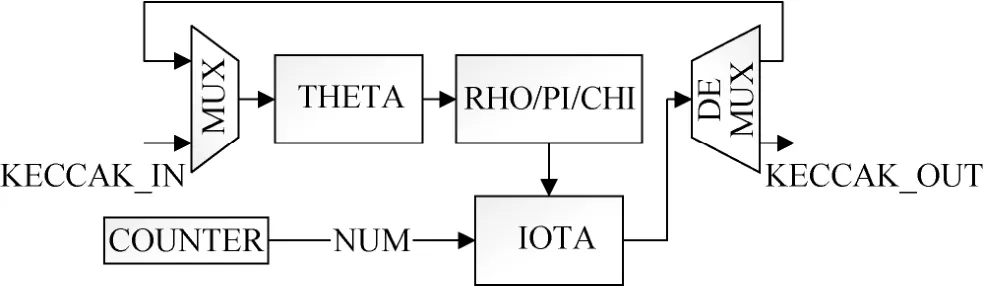
图3 KECCAK模块Figure 3 KECCAK module

3.1.2 HASH_X和HASH_LS模块

由算法2、3、5可知, 在密钥生成过程中, 大致需要两种哈希函数, 一种用于处理定长数据, 另一种处理不定长数据。具体的各哈希函数输入长度如表3所示。

表3 哈希输入数据的长度Table 3 Inputs’ data lengths of HASH function

为了简化不同哈希模块中PAD模块的复杂度并减少硬件资源消耗, 设计中使用了两种哈希模块: HASH_X和HASH_LS。

HASH_X(图4)用于处理字节数为X且X<=1088的定长输入, 包含一个PAD模块与一个KECCAK模块。PAD模块按照NIST标准将输入打包成长度为1088整数倍比特数的数据。LMS过程中, 部分计算模块中的哈希输入一直为定长, 用HASH_X模块实现将降低这些哈希内部PAD模块与控制逻辑的硬件复杂度。由表3可知, 需要处理的定长数据为440比特、432比特和688比特, 故实际使用到的HASH_X为HASH_440, HASH_432和HASH_688。

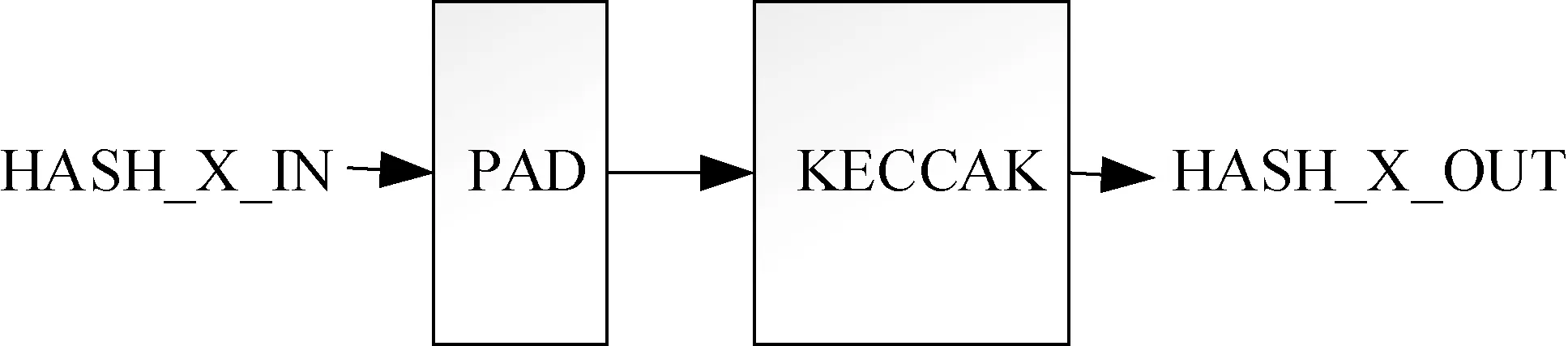
图4 HASH_X模块Figure 4 HASH_X module

HASH_LS(图5)用于处理字节数超过1088比特的不定长数据。输入数据首先被填充(PAD)成为长度为1088比特整数倍的数据, 接着被缓存FIFO (Buffer FIFO)进行缓存和切割为1088比特长度的数据流(STREAM), 再进行后处理。多路选择器(MUX)与多路分配器(DEMUX)用于处理当前KECCAK的输入与输出: KECCAK首轮输入为初始值(INITIAL_ VALUE)与第一个1088比特数的数据的异或值, 其余时刻输入为上一轮KECCAK的1600比特输出状态(STATE)与当前输入的1088比特数据的异或值; 迭代数据达到数据流的个数时, HASH_LS模块输出当前的KECCAK状态值, 作为整个HASH_LS的最终输出值。

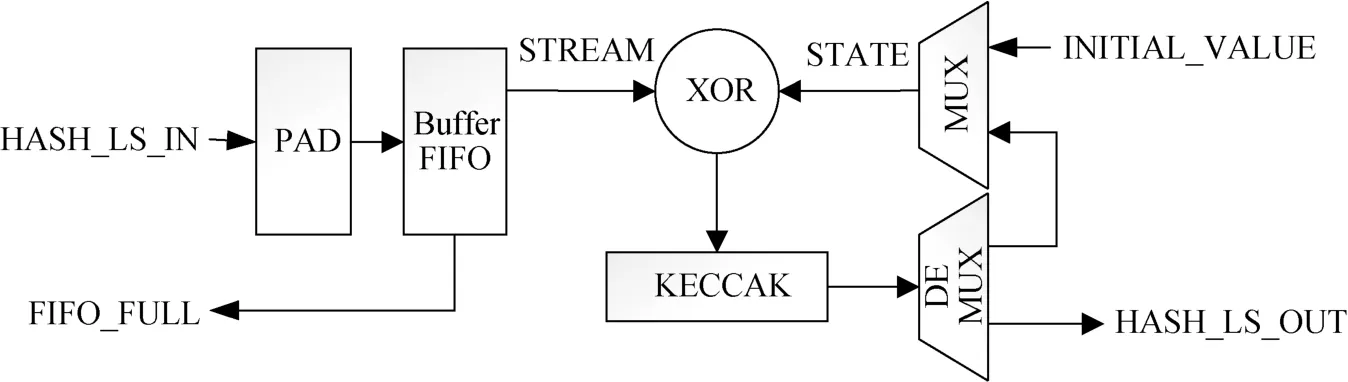
图5 HASH_LS模块Figure 5 HASH_LS module

需要说明的是, HASH_X模块消耗的时钟周期数(Clock cycles)等同于一个KECCAK模块消耗的时钟周期数, 即27个时钟周期。而对于HASH_LS, 输入数据的长度为X(X>1088)时, 内部的KECCAK模块需要进行X1088次计算, 故HASH_LS至少需要27 1088X×个时钟周期数。

3.1.3 HASH_CTR和AXI_HASH模块

针对软硬件协同系统设计的哈希模块需要包含软硬件通信逻辑。在本设计中为HASH_CTR和AXI_HASH模块。HASH_CTR包含GP接口的AXI协议状态机, 接收PS端的开始信号和32bits配置数据。AXI_HASH包含SHA3_256核心运算模块, 外部与FIFO相连, 由FIFO中取数据进行hash运算。

3.2 软硬协同系统设计

面向低功耗应用场景, 使用软硬件协同方案可将原本在ARM核上执行的hash函数卸载至FPGA上, 以降低ARM核的负载, 为ARM核保留更多的运算资源执行其他功能。软硬协同系统的思路为核心哈希运算在FPGA上运行, 其余控制逻辑在软件端执行。本节主要介绍软硬协同系统的顶层设计与软硬件通信逻辑。

3.2.1 系统顶层

如图6所示为软硬件系统的顶层设计, 采用Xilinx公司ZYNQ架构的FPGA开发板, PS (Programming System)端为基于板上的ARM平台的软件逻辑, PL(Progarmmable Logic)端为基于FPGA的可编程逻辑的硬件系统。LMS主体控制逻辑由软件在ARM处理器上实现, 核心运算的HASH模块在FPGA上运行, 两部分之间通过AXI4协议的GP(Global Purpose)接口与HP(High Performance)接口进行数据交换。ARM核执行HASH模块的驱动函数, 控制信号由GP接口传至PL侧控制寄存器中, 数据由HP接口传至PL侧FIFO缓存。HASH_CTR模块处理控制寄存器中的值, 判断是否启动AXI_HASH运算模块, 并配置哈希运算参数。运算结束后AXI_HASH模块将完成信号置“1”, 由HASH_CTR模块采集到该信号之后, 将HASH运算的输出结果与哈希完成的标识值由GP口传输至PS侧DDR中, ARM端监测DDR中标识地址的值, 当监测到完成标识值时, 读取DDR中存放哈希结果地址中的值, 完成一次哈希运算。

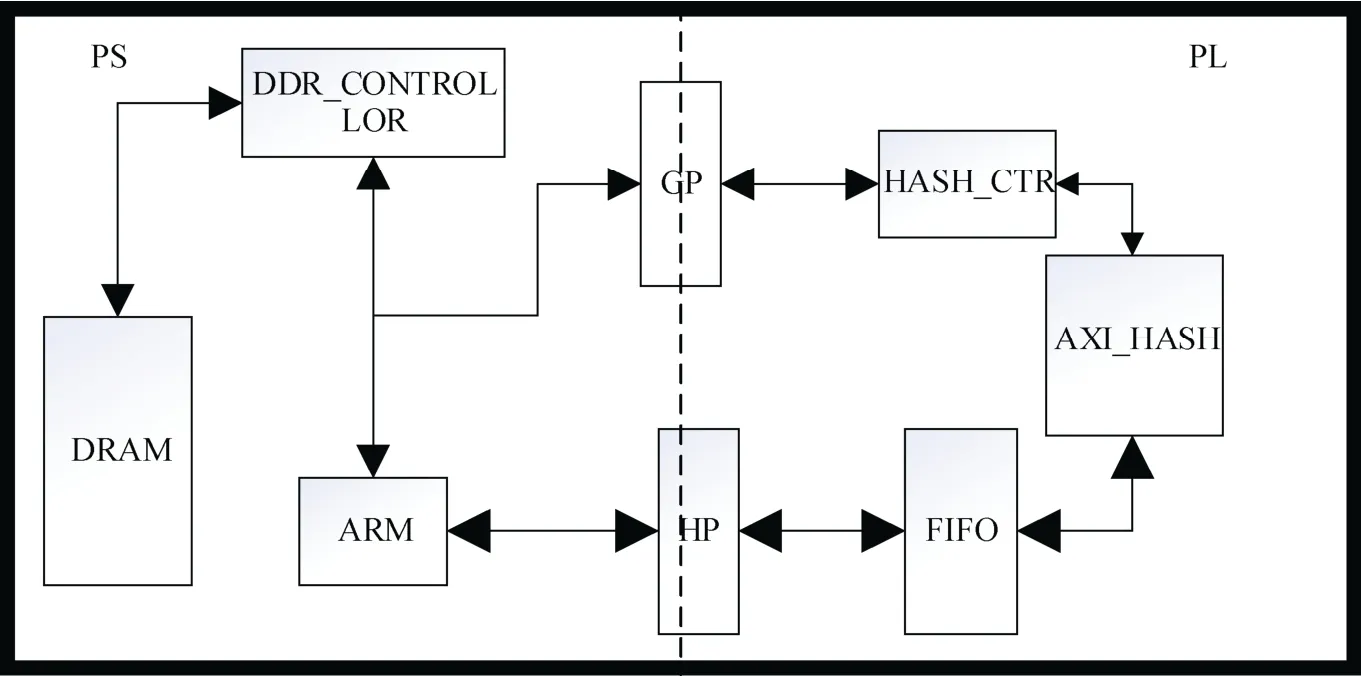
图6 软硬协调系统顶层Figure 6 Overall Design of Hardware-software Co-design

3.2.2 接口设计

为实现PS端与PL端之间的通信, 我们使用DDR中一段固定地址作为通信媒介。使用Linux系统函数mmap(), 将DDR内存中一段物理地址映射到系统中的虚拟地址, 使得系统与PL侧逻辑都能对该段地址内存做读写操作, 从而使得PS端与PL端能够相互通信。

图7为软硬件协同的控制信号通信逻辑图。PS端(C语言实现)将PL端挂在总线上的AXI接口的物理地址通过mmap()函数映射到系统虚拟地址, 并将地址分别分配给enable与valid两变量。Enable和valid的初始值分别为True和False。当valid为FASLE时, PS端将进入循环等待PL端完成哈希运算, PL端完成哈希运算后将valid置为True。 PS端将跳出循环, 并重置enable和valid信号。

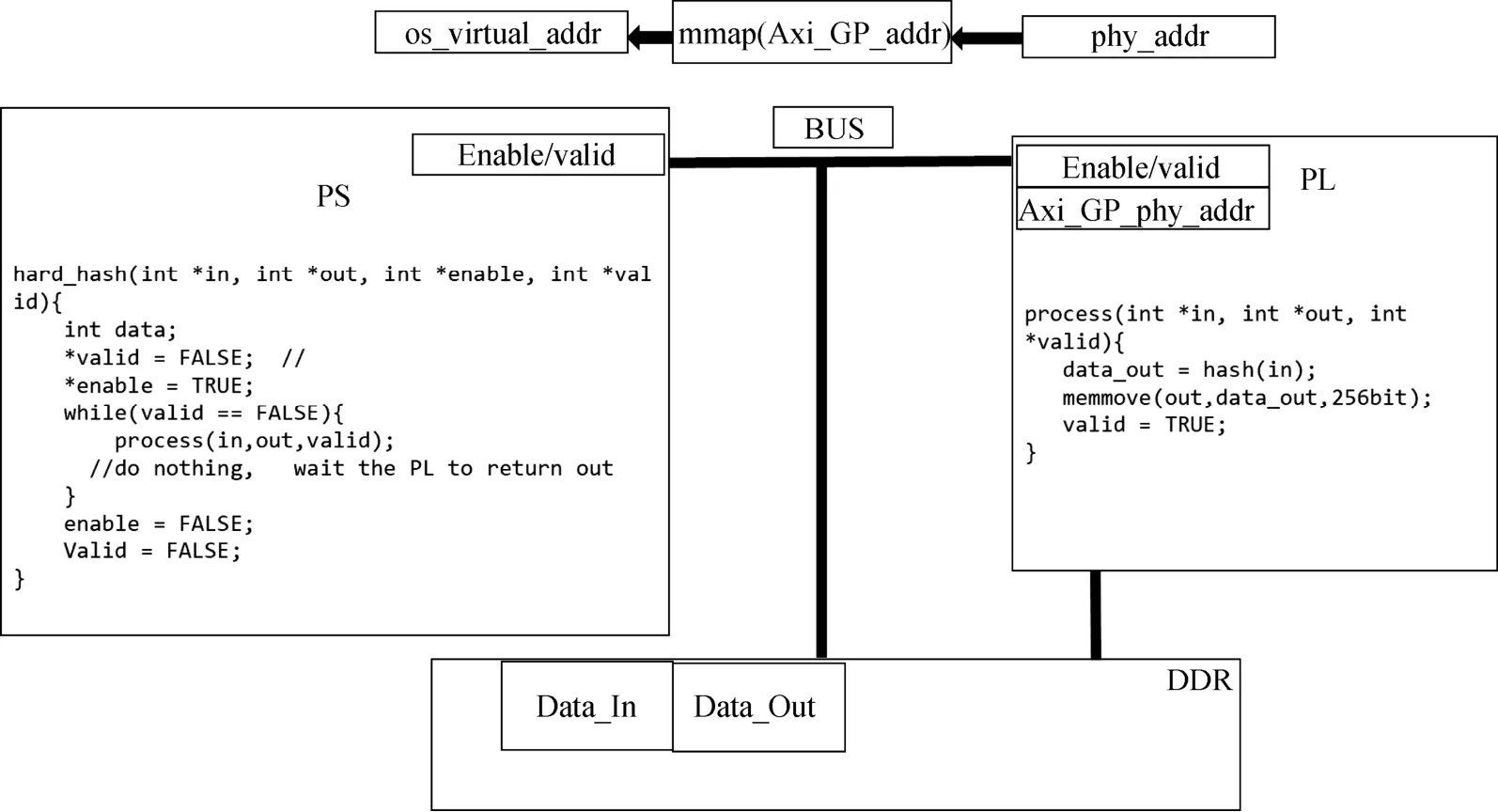
图7 PS端与PL端通信逻辑Figure 7 Communication and control logic between PS and PL

3.3 密钥生成全硬件实现

针对LMS中耗时最长的密钥生成过程, 本工作的硬件设计思路为首先考虑OTS密钥生成的架构设计, 再考虑LMS中的树构造, 即叶子节点与内部节点的计算。

3.3.1 OTS生成y架构 (OTS_Gen_y)

由表3可知, 进行算法2与算法3中生成y序列的计算中, 哈希的输入内容发生变化但长度不变, 均为55字节即440比特, 故硬件上可将计算单元进行复用。因此, 将算法2与算法3中计算y序列的部分合并设计, 并与算法3中最后进行输入不定长的哈希计算的部分拆分开。本小节首先介绍用于实现算法2生成OTS私钥与算法3中生成y序列的模块, 我们称之为OTS_Gen_y模块, 如图8所示。

图8 OTS_Gen_y模块Figure 8 OTS_Gen_y module

首先, 在计算OTS私钥与y序列的过程中, 哈希的输入长度均为55字节即440比特, 故选择HASH_440模块为核心处理单元; 其次, 计算最后不定长哈希的输入中的y序列时, 所需要的最小的迭代组数为p=34, 且p的其余值均为小于34的倍数的临近值。故本工作在HASH_440的处理上选择了34并行。这样设计可以使得各并行模块中的数据实现完全同步处理, 同时实现最大的硬件利用率。

对于每个HASH_440模块, 首轮计算时, 将初始随机值与各模块索引值(index)输入到HASH_440中, 此时HASH_440的输出结果为一个OTS私钥; 在随后的计算中, 将索引值index、迭代次数j与上一轮HASH_440的输出(temp)再次输入到HASH_440模块中。这样迭代 2w–1次后, 索引值为index的HASH_440模块生成的结果对应于算法3中的y序列的y[index]。

对于p=34的参数集, 上述操作执行1轮; 对于p>34的参数集, 这34并行模块中的运算将被执行轮。设这个执行轮数用变量k表示, 则在第k次执行时, 第i个HASH_440的模块的输入索引值为index=34k+i, 如图8所示。

需要注意的是: ①以上述方式, 单个HASH_440的模块可以被复用到OTS私钥生成与公钥生成的两个阶段。且由于LMS中一次密钥生成过程生成的密钥可用于进行2h次有效签名与验证, HASH_440模块的复用将不会对协议的整体效率产生影响。②在p>34的参数集中, 在最后一次迭代时, 部分HASH_440模块本来不需要进行计算, 但在本工作的设计中, 每一轮计算的每个哈希模块都被激活以进行运算。如p=133时, 需要执行k=4轮计算, 而在第4轮计算时, 34个模块中的第32、33、34模块仍在进行计算, 但输入输出的结果均为无效值。这样设计的好处是, 哈希计算时尽量实现恒定功率, 以此可以一定程度上抵御功率攻击。

3.3.2 LMS公钥生成架构

前一部分已经包含LMS私钥生成的过程, 这里介绍LMS公钥生成的模块, 也是本工作架构中的顶层模块。如图9所示, LMS公钥生成模块将LMS公钥生成分为叶子节点生成(LMS_LEAF_GEN)和树生成(LMS_TREE_GEN)两部分。

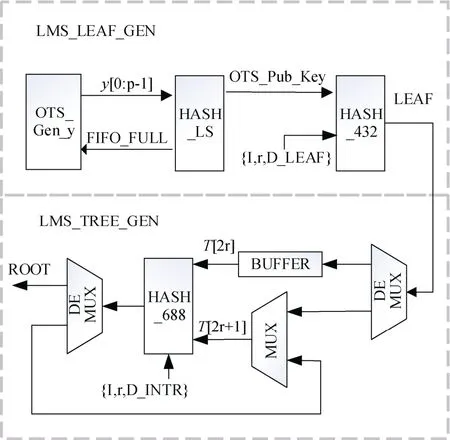
图9 密钥生成顶层设计Figure 9 Top design of key generation

叶子节点生成(LMS_LEAF_GEN): 首先, 当OTS_Gen_y产生y序列后, 序列中p个256比特的数据被填充、打包成单位为1088比特的数据流并输入到HASH_LS模块中, 用以计算OTS公钥值中的K。当 HASH_LS内部的 Buffer FIFO 满时, 向OTS_Gen_y模块输入FIFO满信号(FIFO_FULL), 用以暂停OTS_Gen_y模块的输出, 注意为尽可能保持功率稳定, OTS_Gen_y内部的运算不会停止, 而是在FIFO_FULL无效之前, 进行数据不变的运算。同时, 一旦OTS_Gen_y开始输出有效数据, HASH_LS模块开始进行运算, 而当所有的y都输入到HASH_LS模块, HASH_LS模块计算产生有效的K值后,K被用于组成OTS的公钥值(OTS_Pub_Key)。由表3可知, 该公钥值与叶子节点的索引值、D_LEAF等参数组合成长度为432比特的数据, 输入到HASH_432模块用以计算叶子节点的值。

树生成(LMS_TREE_GEN): 考虑到叶子节点的生成是间歇的, 在构造内部节点的过程中采用深度优先的思路, 即对于当前输入的叶子节点, 不断计算内部节点知道不可再计算父节点为止。

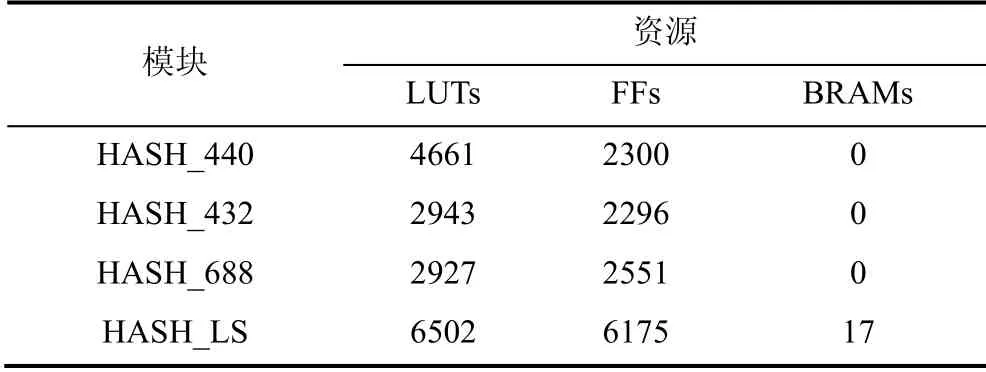
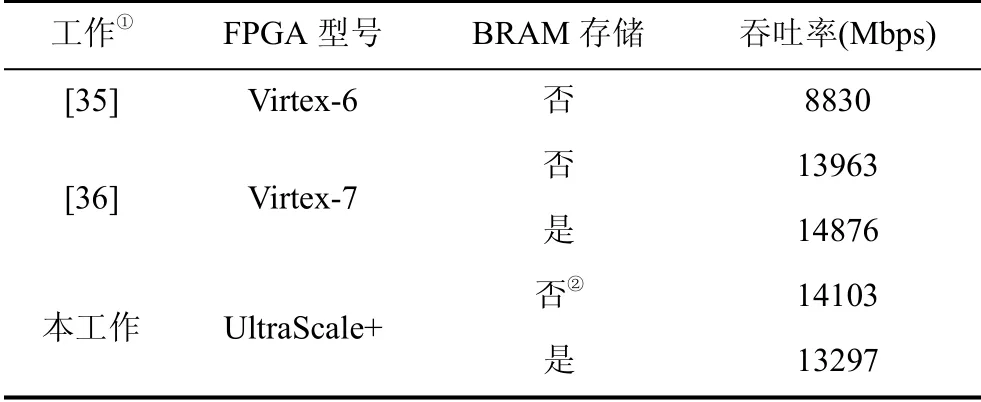
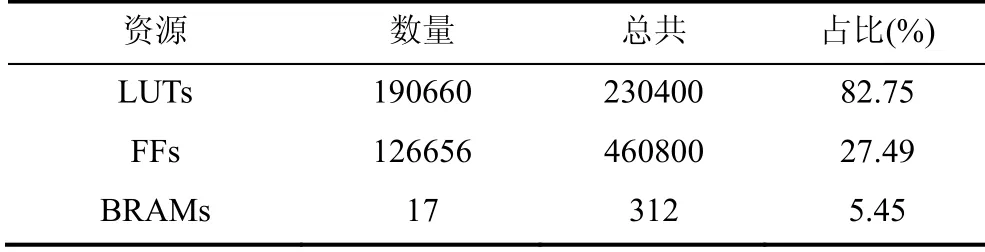
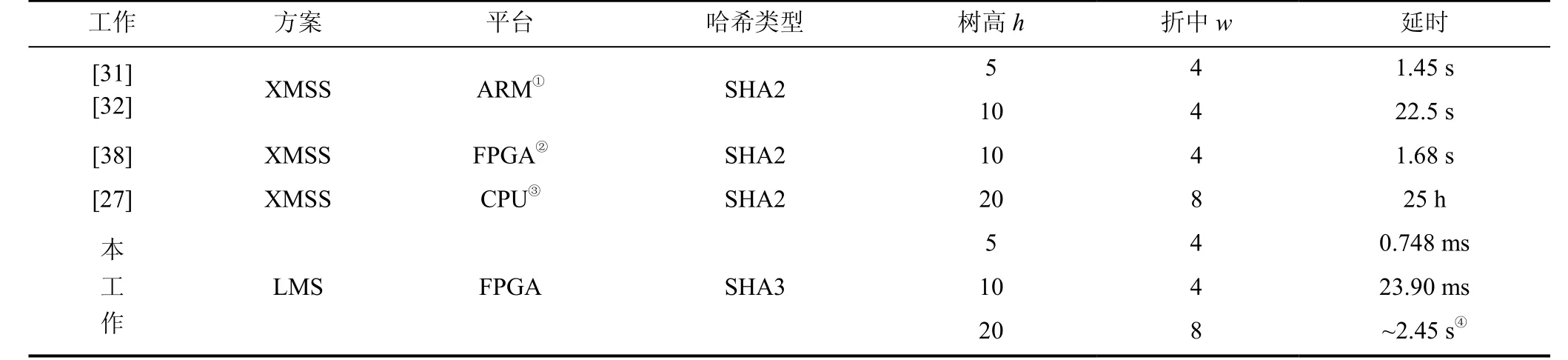
首先使用一组缓存的寄存器(BUFFER), 此组寄存器的尺寸为h×256比特。为方便叙述, 将寄存器的每个单位称为BUFFER[i],其中BUFFER[i]都是256比特且0

由于本文的初步工作[33]中没有对此架构支持的极限树高进行说明, 在此进行补充分析与说明。当树高h小于一定阈值时, 不会出现叶子节点数据输入到树生成模块中但未被计算到的情况。考虑到叶子节点的计算需要2w个HASH_440模块延时(1次计算OTS私钥, 2w–1次计算OTS公钥), 1个HASH_LS模块延时和一个HASH_432延时; 而内部节点的计算最多进行h次HASH_688计算, 且进行h次计算时是在计算最终的根节点T[1], 即计算其他内部节点时最多需要h–1次HASH_688模块的延时。由章节3.1.2可知, HASH_440、HASH_432、HASH_688消耗的时钟周期数均为27, HASH_LS消耗的时钟周期数为时钟周期数分析见表4。如果出现叶子节点的输入快于内部节点计算, 则有 1>h-2。结合表1, 可能出现上述情况的h最小需满足有h>34(此时p=67,w=4)。但根据表2, 目前h的推荐最大值为25。故在推荐参数集中, 本设计中的树生成模块可以在不遗漏数据的基础上完成最快计算。

表4 叶子节点与内部节点计算的时钟数Table 4 Computing clock cycles of leaf nodes and internal nodes

3.4 安全性分析

本文工作中将原LMS方案的核心计算函数即SHA2函数替换成了SHA3函数, 对于这样的替换, 需要对安全性进行分析。

3.4.1 SHA2 vs SHA3

从哈希的安全性角度, 在NIST相关标准文件[12]中提到, SHA3具有SHA2函数的所有安全性性能, 包括128比特安全强度的抗碰撞性(Collision resistance)和256比特安全强度的抗原像攻击性(Preimage resistance)。而在抗2级原像攻击性(2ndpreimage resistance)方面, SHA3函数的安全强度为256比特, SHA2函数的安全强度为256–L(M)比特, 其中M是输入数据比特数,L(M)是一个关于M的非负正相关函数。也就是说, 输入数据越长, SHA3的此项安全性性能越优于SHA2函数,L(M)具体计算公式见(12)。

3.4.2 LMS安全性

对于包括LMS在内的HBS方案, 协议的安全性完全取决于其中采用的哈希函数的安全性[10,16-19]。理论上来说, OTS中采用的哈希函数和LMS树的内部节点采用的哈希函数可以不同, 但为了防止出现更弱哈希函数被攻击的情况, 更建议采用相同的哈希函数[23], 如LMS原方案及现有的相关工作均采用SHA2函数。因此, LMS方案的安全性完全取决于内部采用的单一哈希函数的性质。而在IETF公开的LMS文献中[23]提到, 当前的参数设置可支持多种哈希函数如SHA256(即SHA2)和SHA3函数, 故在安全等级保证不变的前提下, 替换哈希函数并不 会产生多余的安全性损失。

4 性能评估

性能评估方面, 软硬协同系统硬件端和设计的硬件架构部分用verilog进行实现, 综合与实现过程采用了Xilinx Vivado 2019.2 版本的EDA工具, ARM和FPGA平台选择Xilinx Zynq UltraScale+ MPSoC ZCU104开发板。

4.1 软硬协同系统

对于软硬协同系统, 硬件端资源(表5)消耗5013个查找LUT(Loop up table, LUT)和9838个触发器(Flip flop, FF), 分别占到FPGA芯片总资源的2.17%和2.13%。需要说明的是, 在不同参数写的硬件端资源消耗是一致的(包括不定长哈希模块与相关接口配置)。

表5 软硬件协同系统资源消耗Table 5 Resource consumption of the Hardware-software Co-design

在w=8且h=5的参数下, 软硬件协同系统需要9 s左右完成密钥生成。其中主要的时间消耗在FPGA与ARM的通信过程。对于时间性能, 由于目前只在硬件端部署了一个哈希模块, 比起核心计算, 软硬件通信过程消耗了更多时钟数, 总体计算时间消耗较长; 且随着w, h增大, 软硬件协同系统生成密钥所需的计算时长将增加得更快。因此, 目前本文给出一个较小尺寸的参数下的时间性能, 由于这是针对LMS软硬协同系统的首次探索, 该性能可以为后续工作提供物联网应用场景下实现LMS的时间性能参考。

4.2 密钥生成架构

对于密钥生成的硬件架构, 需要说明的是, HASH_LS模块中使用的FIFO尺寸为64×1088比特; 树生成模块中的BUFFER尺寸为32×256比特, 即允许的最大树高为32。为了直观地体现本工作的优势, 将我们所设计的架构对表1所示的所有参数集与表2中的部分参数集进行了仿真与延时计算, 并在Xilinx Zynq UltraScale+ ZCU104的开发板上进行了实现。

4.2.1 哈希计算模块

首先, 在实现结果中, 在最大工作频率下, 几种不同尺寸的哈希模块的资源占用情况如表6所示。在查找表与触发器的资源占用上, HASH_X模块与HASH_LS模块出现了明显的数量差异。同时, 由于HASH_X模块不需要进行数据缓存, 不需要额外占用块存储器(Block RAM, BRAM)。因此, 对哈希模块进行分开设计达到了节省硬件资源的结果。

表6 哈希模块资源消耗Table 6 Resource consumption of HASH modules

为了更直观地说明本工作中哈希模块的高效性, 对哈希进行最大时钟频率下吞吐率的计算, 并选取相关工作的结果进行对比, 如表7所示。由表可见, 本工作中哈希模块的吞吐率与相关工作可达到相当的吞吐率。且由于本工作中将根据LMS方案内部计算的特性, 对哈希模块进行相匹配的设计与部署, 可增加整个方案的资源利用率。

表7 哈希模块吞吐率对比Table 7 Comparisons of throughputs of HASH modules

4.2.2 密钥生成架构

对于整个密钥生成架构, 在最大时钟频率达到285MHz的基础上, 资源消耗情况如表8所示。由表可知, 本文中提出的硬件架构在硬件资源上, 分别消耗了82.75%的查找表、27.49%的触发器和5.45%的块存储器资源。

表8 密钥生成资源消耗Table 8 Resource consumption of the key generation design

目前还没有关于LMS协议密钥生成的FPGA硬件实现。所以, 本文选取已有的基于其他平台的工作来进行对比, 结果如表9所示。需要注意的是, 由于文献[29]和文献[30]的CPU实现结果已经优于文献[23]中结果, 在此不再对比文献[23]中性能。由表可知, 本工作中的密钥生成架构相较于目前最新的工作实现了超过一个量级的加速比。

表9 与以前工作的密钥生成延时对比Table 9 Latency comparison of key generation with previous works

由于以前的工作可对比的参数不足且没有核心计算替换为SHA3的LMS实现, 我们还进行了软件评估, 并将本工作的FPGA实现与软件实现进行对比。对于软件实现, 将标准参考文档[23]提供的开源代码[37]中的SHA2_256哈希函数换成SHA3_256函数, 并在Intel(R) Core(TM) i7-6850K 3.60GHz CPU进行了允许多线程的实现。本工作与该CPU的延时对比如表10所示。

表10 CPU与FPGA实现的延时对比Table 10 Latency comparison of implementation on CPU and FPGA

可以看出, 本工作的FPGA实现相比于目前较优的CPU实现, 在不同的参数下, 具有55~2091倍的速度提升。当h=5且w<8的时候, 速度提升浮动较大, 经过分析, 我们认为原因是, 软件实现中虽然计算量减小但CPU中一些必要的控制没有随之减少, 故FPGA实现的速度提升倍数尤其大; 而当h或w更大的时候, 相同的w对应的速度提升倍数趋于稳定, 更具有参考意义。

4.2.3 与XMSS的比较和讨论

由于LMS和XMSS方案的相似性, 在LMS现有可比较工作不足的情况下, 与相近的XMSS方案的相关工作比较也具有一定的参考意义。对于XMSS方案, 目前已经出现较多的实现与优化工作[18,26-27,31-32,38-39], 但相似地, 这些工作较多集中于签名和验证过程。我们整理了目前文献中最新的XMSS密钥生成过程的性能数据[27,31-32,38], 在相同安全等级、相似参数配置的基础上与本文架构相比较, 结果如表11所示。可以看出, 在现有参数对比下, 相较于XMSS的软件实现, 本工作中架构实现了超过两个量级的加速比; 相较于XMSS的FPGA实现, 本工作中架构实现了约70倍的加速比。从这项对比中, 进一步说明本工作所实现的硬件加速器的高效性。

表11 与XMSS的密钥生成延时对比Table 11 Latency comparison of key generation with XMSS

5 总结

本工作首先在不损失安全性的前提下, 对LMS中核心的SHA2函数替换成SHA3函数, 为LMS的灵活配置方面进行了探索; 接着, 在本文中首次提出了整个协议的软硬协同系统; 该软硬协同系统在占用较少资源的基础上, 可在整个LMS过程进行使用并通过验证, 为后续LMS进入物联网场景下的实际应用提供了参考。同时, 针对最耗时的LMS密钥生成的过程, 提出了一种快速、可扩展的基于FPGA的硬件加速器。在该加速器设计中, 许多优化方案被用于增加并行性和可伸缩性, 并减少延迟。架构被设 计为在允许不同的参数集的情况下, 仍然保持恒定功率。该结构在FPGA上的实现结果表明, 新的硬件实现在速度性能上大大优于传统的CPU实现。

未来, 我们将关注LMS软硬件协同系统中密钥生成模块全卸载至FPGA上的加速方案, 以及LMS中签名与验证的硬件加速等。

致 谢感谢国家自然科学基金资助项目(No.61774082)、中央高校基本科研业务费专项资金资助项目(No.021014380065)、江苏省重点科研计划资助项目(No.BE2019003-4)对本文的资助。