应用于后量子密码的高速高效SHA-3 硬件单元设计

刘冬生, 陈 勇, 熊思琦, 杨 朔, 胡 昂

华中科技大学光学与电子信息学院 武汉 中国 430074

1 引言

量子计算机技术和量子算法的不断发展为现有的经典密码体制的破译提供了更有力、更致命的攻击方法, 使其不再有足够的安全性保障现代社会的信息安全。如著名的Shor量子算法可以在多项式时间内分解大整数和求解离散对数, 因此对于传统公钥密码体制如RSA、ECC、DSA、ElGamal等, 采用增加密码长度和参数大小来抵御安全攻击的方式也不再有效。为了抵御量子计算机的攻击, 后量子密码(Post-Quantum Cryptography, PQC)应运而生。

2020年7月, 在NIST公布的后量子密码标准候选算法第三轮筛选中, 基于格的算法占据主导地位[1]。格密码在安全性上能抵御已知的量子攻击, 且具有公钥小, 计算速度快, 功能多样的优点, 更易于集成化、小型化、芯片化。因此, 基于格的PQC方案具有重要的研究与应用价值。在众多格密码方案中, SHA-3作为其中重要的核心算子不仅可以对关键信息进行散列, 同时可以产生随机数比特流, 从而用于采样模块生成满足条件的采样值。表1显示了应用于最新一轮评选的后量子密码方案的SHA-3函数家族。可以看到, 进入第三轮评估的PQC方案中至少用到了一种SHA-3函数。在诸多格密码方案中, SHA-3函数是通用的核心算子, 占用了约20%以上的资源开销和处理周期[2-3]。

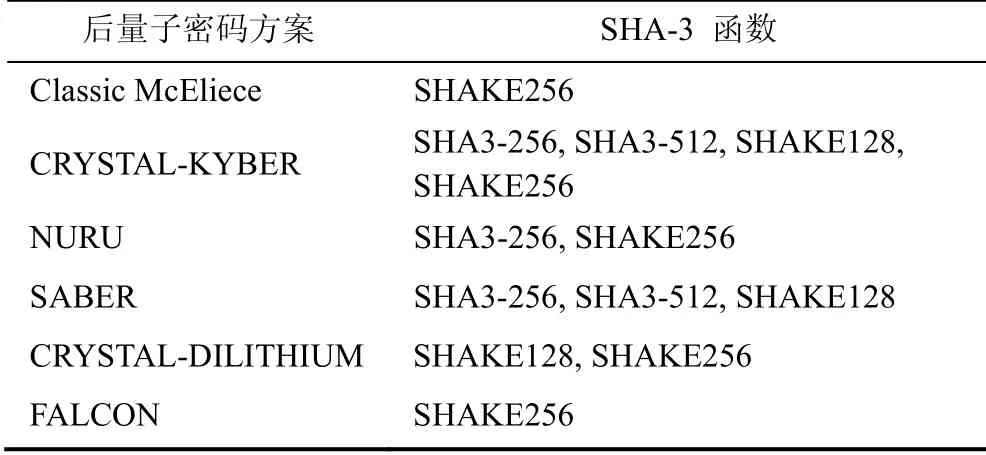
表1 第三轮后量子密码方案中的SHA-3函数Table 1 SHA-3 in third-round PQC schemes

自Keccak算法被评选为第三代安全散列算法(Secure Hash Algorithm-3, SHA-3)以来, 国内外对该算法的研究热度不断提升。根据不同的目标平台和实现要求, 在SHA-3算法的优化方向主要集中在以下三个方面: 更低的资源开销[4-5], 更高的实现性能[6-7]以及性能面积的折中设计[8-9]。

本文从SHA-3的原理出发, 研究了应用于格密码的高速高效的SHA-3硬件实现和优化, 提出了一种全新的展开级流水线结构。本文首先介绍了SHA-3关键环节的原理, 然后提出了SHA-3的硬件实现方式, 具体包括轮常数的简化存储以及新型的流水线技术, 并在此基础上运用了展开的结构完成了SHA-3高速高效的硬件设计, 最后给出了本设计在FPGA上的实践过程和结果以及与前人工作的对比。

2 SHA-3算法分析

哈希函数是把任意长度的输入消息串变化成固定长的输出串且由输出串难以推算输入串的一类函数。其安全性主要体现在抗碰撞攻击、抗原象攻击和抗第二原象攻击三个方面。在SHA-3算法的评选过程中, 由意法半导体公司的Guido Bertoai Bertoai、Jean Daemen Daemen、Gilles Van Assche Assche与恩智半导体公司的Micha Michaëël Peeters 联合设计的Keccak算法由于采用了不同于传统Merkle- Damagard结构的新型海绵结构, 具有可证明的良好安全性, 并且很容易在安全强度和处理速度之间取得平衡, 因此在2012年被确定为SHA-3的获胜算法[10]。

SHA-3算法最终提交的是Keccak-f[1600], 迭代轮数为24轮。该算法的新颖之处在于提出的新型海绵结构。海绵结构使用有限的状态, 接收任何长度的输入位流且能满足任何长度的输出。该结构主要由内部函数f、分组位长度r和填充算法pad这三组参数定义。海绵结构分两个阶段进行处理: 吸收阶段和挤压阶段。在吸收阶段, 先采用多重位速率填充的方法对输入的数据进行填充, 再将填充后的消息分为M1, M2, … , Mn共n块, 每块为r位, 依次将该消息块依次与产生的r位内部状态做异或, 然后将Keccak-f[1600]函数作用于该状态, 生成的新状态再与下一消息块进行同样的操作。如图1所示, M1先与海绵结构的初始状态(空状态)异或并输入f函数进行处理并产生输出, M2再与该输出异或, 如此循环往复n次, 直到所有的消息块都被处理, 之后进入压缩阶段。在压缩阶段中, 若所需输出消息摘要长度短于吸收阶段的输出, 则直接截取相应长度, 跳过此阶段; 反之, 则需再执行Keccak-f[1600]函数, 并将结果串联起来, 直到得到所需长度的输出。

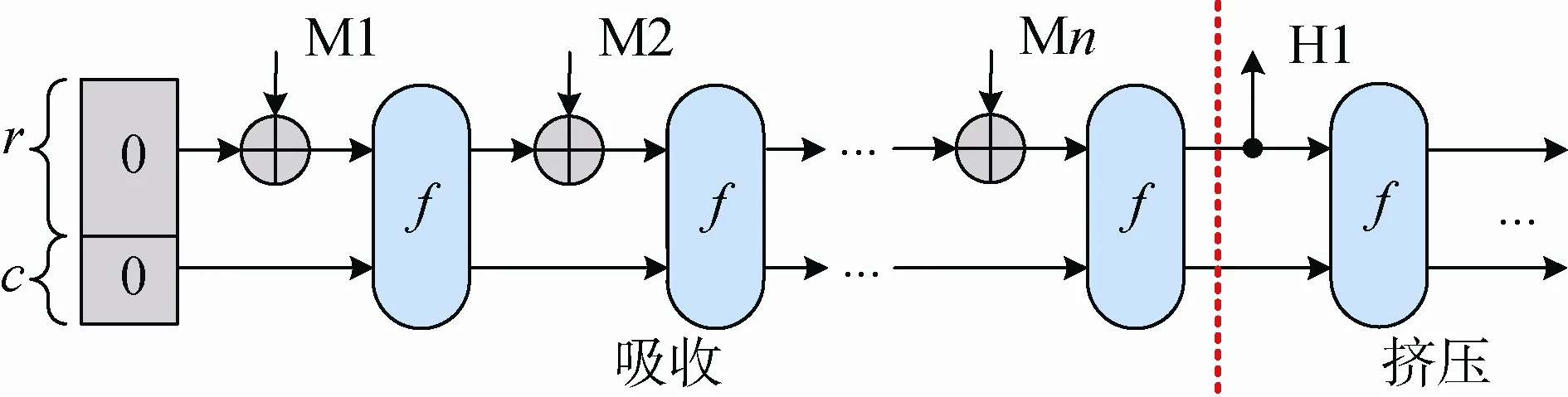
图1 海绵函数结构Figure 1 Sponge construction of Keccak

迭代轮函数的实现过程如下: 在置换函数f中, 取1600-bits状态, 将其转换为一个5*5*64的三维数组作为输入, 并基于该数组进行24轮变换, 每一轮变换包括θ,ρ,π,χ,ι5个步骤。Keccak-f[1600] 5个步骤中的前4步都是在三维状态矩阵中进行不同方向的行(row)列(column)和道(lane)变换, 将所有元素混淆和扩散。而最后一步是将一组各不相同的轮常量添加到元素中以打破其他4个变换的对称性。下式为变换步骤的表达:

表2表示了步骤ι中所采用的轮常数。

表2 轮常数值(16进制)Table 2 Value of round constants

3 SHA3硬件设计

3.1 轮常数的简化

在Keccak-f[1600]五轮算法中的最后一轮ι变换中采用了轮常数与S[0,0]道元素相异或以打破原有变换对称性的形式。通过表2可以分析出, 在这24组64位轮常数中只有其中的0, 1, 3, 7, 15, 31 和63位可能产生变化, 而余下的57位均为零。为了减少运算量以及存储空间, M. M. Wong[9]提出了将64比特轮常数SRC(simple round constants)简化为8比特的方法, 在本文设计的硬件结构中, 进一步将其压缩为7比特, 简化后的轮常数见表3。

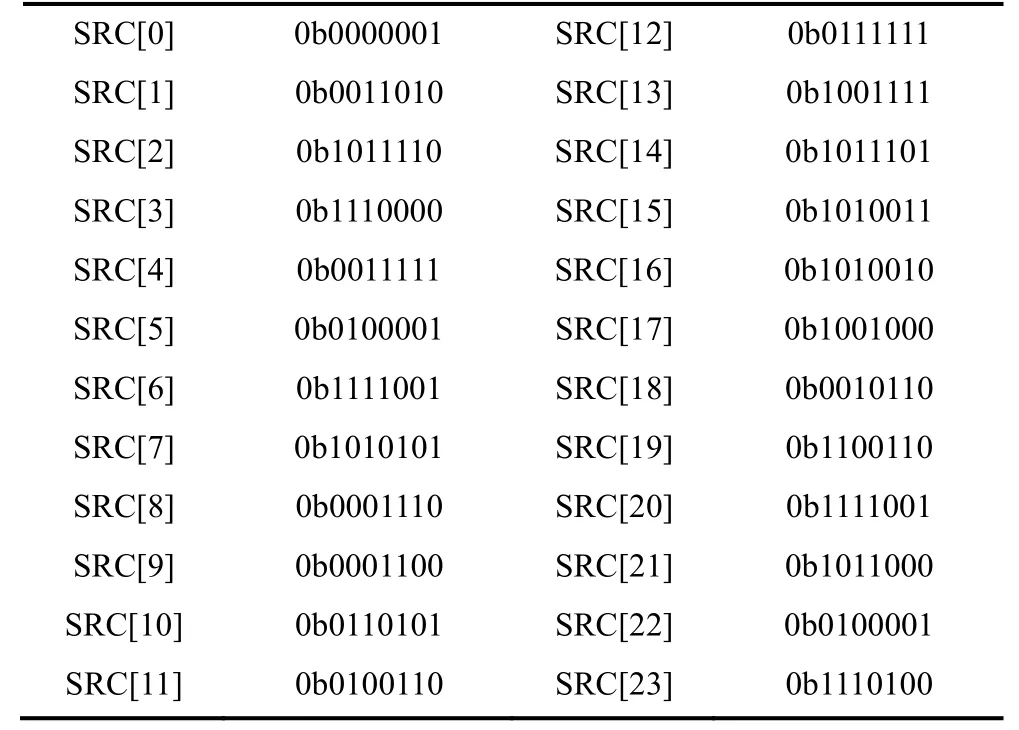
表3 简化的轮常数(2进制)Table 3 Value of simplified round constants

仅存储7个非零位的优势如下:

(1) 降低资源消耗: 将原有的64位缩减为7位, 所需寄存器大幅缩减, 硬件开销减小了90%左右;

(2) 简化计算: 轮常数用于参与异或运算, 采用本设计中的简化值, 只需要运算SRC中的7位与S[0,0]中对应元素的异或结果, 其他位直接输出原值即可。

3.2 改进的流水线技术

在SHA-3的硬件结构设计中一般采用流水线结构, 基于流水线技术, 在Keccak的轮函数算法中数据可以并行传输, 这对于提高系统的时钟频率和增加数据吞吐量有明显的优势。但与此同时, 硬件开销也会相应增加。在硬件设计过程中, 流水线寄存器一般插入在轮与轮之间或者每轮内部[11], 以减小决定运行时延的关键路径。亟待解决的问题是, 如何改进流水线结构以达到硬件开销和运行时间的相对平衡, 实现功耗和性能的折中。

目前普遍的解决方案是插入两组流水线寄存器, 分别位于每轮结束的输出端和迭代函数变换的步骤间。常规方法是在θ变换和ρ变换之间插入流水线寄存器[6,9], 如图2(a); 或在π变换和χ变换之间插入流水线寄存器[12-13], 如图2(b)。由于ρ变换和π变换只涉及移位操作, 没有逻辑门参与运算, 因此这两种方法在关键路径的改善上并无区别。但在本文提出的 结构中, 通过改变流水线寄存器的位置, 可以将关键路径进一步缩短, 使得整个流水线架构的性能大幅提升。

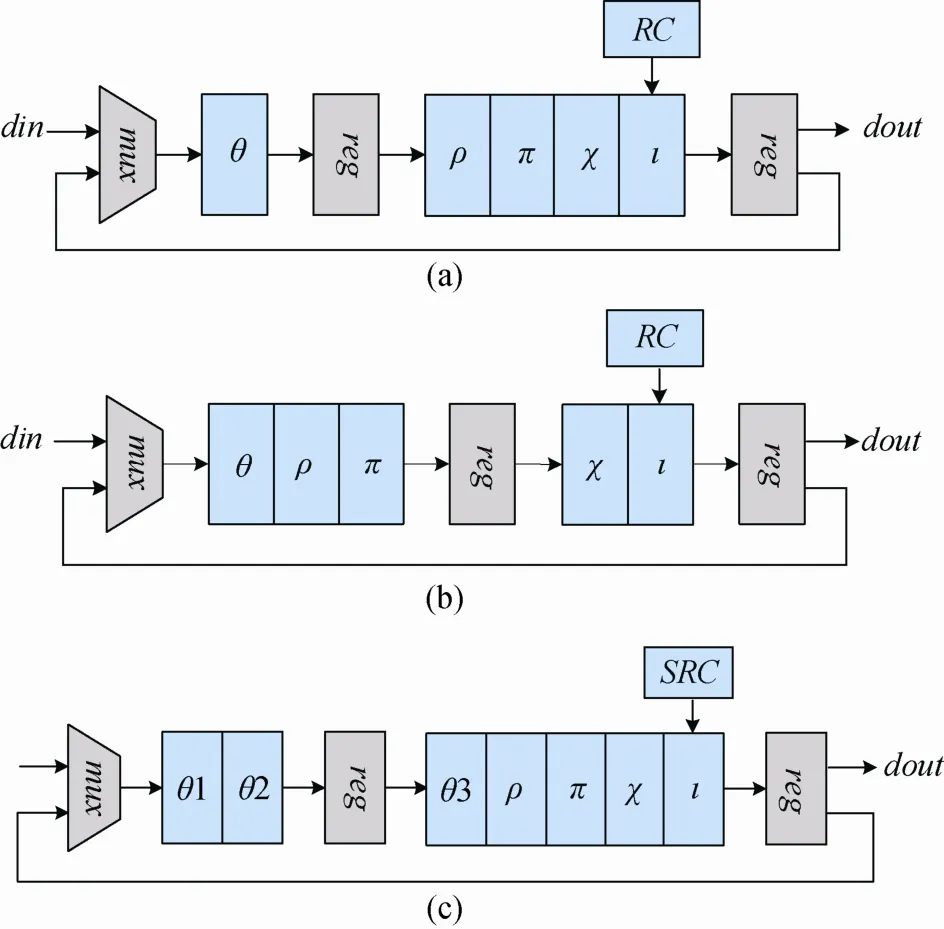
图2 传统的流水线结构(a)(b)和改进后的流水线结构(c)Figure 2 Conventional pipeline structure (a)(b) and proposed pipeline structure(c)

改进的流水线结构如图2(c)所示, 本设计同样采用了两组流水线, 第二组寄存器仍然位于每轮结束的输出端, 第一组寄存器也安插在轮变换结构的内部。不同的是, 本设计将θ变换分为三个步骤(θ1,θ2,θ3), 并将该组流水线寄存器插入θ2和θ3之间,θ1~θ3的变换如式(1)~(3)所示。从式(1)~(6)中可以看出, 每个步骤需要的逻辑门数量如下: (1)θ1操作需要4个异或门; (2)θ2操作需要1个异或门; (3)θ3操作需要1个异或门; (4)ρ和π变换不需要逻辑门; (5)χ变换需要1个异或门、1个非门和1个与门; (6)ι变换需要一个异或门。因此, 如果把流水线寄存器插入θ变换和ρ变换之间或π变换和χ变换之间, 则关键路径上的运算要经过6个逻辑门, 而在本文提出的结构中, 二级流水的第一级包含θ1和θ2变换的5个异或门, 第二级由θ3、ρ、π、χ和ι变换中的3个异或门、1个非门和1个与门构成。由此可见, 把流水线寄存器插入θ2变换和θ3变换之间, 则将关键路径上的逻辑门由6个缩减为5个。

具体结构如图3, 该电路将1600-bits的输入平均划分为25组, 每组64-bits, 将其输入迭代运算模块参与θ、ρ、π、χ和ι运算, 产生1600-bits的输出, 再将其输出作为下一个循环的输入, 如此往复24轮, 得到最终的输出。在此过程中, 流水线寄存器插入在θ2和θ3之间以及每轮的输出端, 使得流水线的两个部分最长路径均经过5个逻辑门。值得注意的是, 与传统结构相比, 该设计在θ3部分增加了5个64-bits 寄存器, 以保证时序和运算结果的准确性。虽然增加寄存器带来了一些额外的硬件开销, 但其带来的运行速度上的优势是更加显著。

3.3 SHA-3架构

提高吞吐量一般有如下两种方法, 展开和流水线结构。所谓展开是指在一个时钟周期内实现Keccak-f[1600]的多轮迭代。比如原有一个时钟周期只能实现一次迭代运算, 因此执行Keccak算法的24轮迭代需要24个周期; 若经过展开之后每周期迭代运算的数量增加为两个, 则实现24轮的迭代只需要12个时钟周期。缺点是, 相应的资源消耗也增加了一倍。而上文所提到的流水线技术, 不仅可以在迭代轮内部增加流水线寄存器, 也可以将其插入展开后的迭代轮之间, 以提高运行效率。如何将这两种技术结合起来, 确定展开因子和流水线的组合方式, 以达到低功耗和高性能的折中, 是本设计中所解决的问题。

更高的展开因数和流水线级数可以带来吞吐量更大的提升, 但是同时会带来硬件资源开销的成倍提升, 使得硬件效率反而下降。经过评估和比较各种不同的硬件结构, 本设计选择了展开因数为2的硬件结构。此种结构既实现了高吞吐量, 同时保持了较低的资源开销, 能实现最大的硬件效率。其中两个内部流水线寄存器(inside pipeline registers, IPR)位于迭代运算单元内部, 两个输出流水线寄存器(output pipeline registers, OPR)位于相邻迭代运算单元之间。同时, 上文所讨论的简化的轮常数与改进的流水线结构在该结构中也有所体现。

如图4所示, SHA-3的核心硬件结构由主要由控制单元和两个迭代运算单元组成, 每次轮转可以进行两轮迭代运算, 完成24次迭代运算仅需12次轮转。控制单元用于控制SHA-3的工作进程, 而每个迭代函数用于实现Keccak-f[1600]中θ,ρ,π,χ,ι5个运算步骤。除迭代函数5个步骤对应的硬件电路之外, 迭代运算单元内部在θ2和θ3之间插入了IPR, 两个迭代运算单元的输出端也有OPR。

图4 SHA-3核心硬件结构Figure 4 SHA-3 hardware architecture

工作过程如下:

(1) 输入: 1600-bits数据通过din端输入二路复用器, 由控制单元决定并判断输入迭代运算单元1的数据来自din端或者二路输出选择器的反馈;

(2) 迭代运算单元1: 数据依次经过θ,ρ,π,χ,ι5个运算步骤, 其中参与ι运算的SRC为偶数轮的轮常数(SRC0, SRC2,…,SRC22), 控制单元根据轮数选择特定的轮常数通过十二路复用器输出, 在ι步骤中与S[0,0]道的数据相异或, 再从迭代运算单元中输出, 进入OPR;

(3) 迭代运算单元2: 经过OPR后数据进入迭代运算单元2, 与迭代运算单元1不同的是SRC为基数轮的轮常数(SRC1, SRC3,…,SRC23), 其他步骤相同。输出之后经由OPR输入二路选择器;

(4) 循环及输出: 由控制单元根据时钟周期和轮数判断输出是否为最终输出, 若满足24次迭代运算, 则通过dout端输出, 若仍在迭代周期内, 则跳转至步骤(2), 继续循环直到满足条件。

4 实验结果及对比

本文中的设计采用Verilog-HDL编写, 环境是Xilinx ISE 14.7 Design Suite, 在Xilinx Virtex-6的XC6VLX75T-2ff784 FPGA上完成了验证。

表4展示了本设计与其他相关文献中设计的指标参数对比, 吞吐量和效率的计算方法如式(7)(8)所示。其中r代表比特率(bitrate), 在SHA3-512中r等于576,f代表最大频率,N代表同时处理的数量块数量, 此结构中为4,cycles代表运算周期数, 此结构中为48,area代表硬件资源消耗。

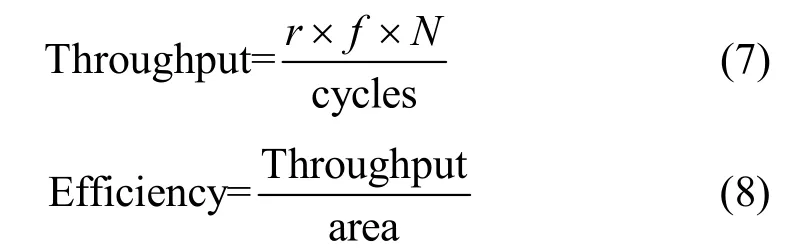
如表4所示, 本设计中的SHA-3硬件架构在Virtex-6 FPGA上最大工作频率达到了459 MHz, 吞吐量达到了22.03 Gbps。此外, 本设计共消耗硬件资源1498 Slices, 实现了14.71 Mbps/Slices的高效率。

表4 基于SHA3-512与相关工作的比较Table 4 Comparison result of SHA3-512 with related works

图5显示了与一些先前工作的比较结果。其中, Michail[17]在使用4个OPR展开4次时实现了最高吞吐量。M. M. Wong[9]在分别使用两个OPR和IPR并进行两次展开时达到最高效率。值得注意的是, 流水线级数和展开因子的增加使得吞吐量更高, 但资源消耗将相应增加。Michail[17]具有较高的展开因子和流水线级数, 但文中所达到的高吞吐量是以巨大的硬件开销为代价的。本设计的目标是提高吞吐量, 同时尽可能降低资源消耗, 因此没有选择更高的流水线级数或展开因子。本设计与M. M. Wong[9]中的2个IPR和2个OPR具有相同的两次展开架构, 但由于简化轮常数的应用和新型的流水线技术, 提高了33.4%的吞吐量和28.2%的硬件效率。由此可见, 与以前的工作相比, 在包括最大频率、面积、吞吐量和效率在内的主要性能指标中, 本设计的频率和效率达到了最佳水平。

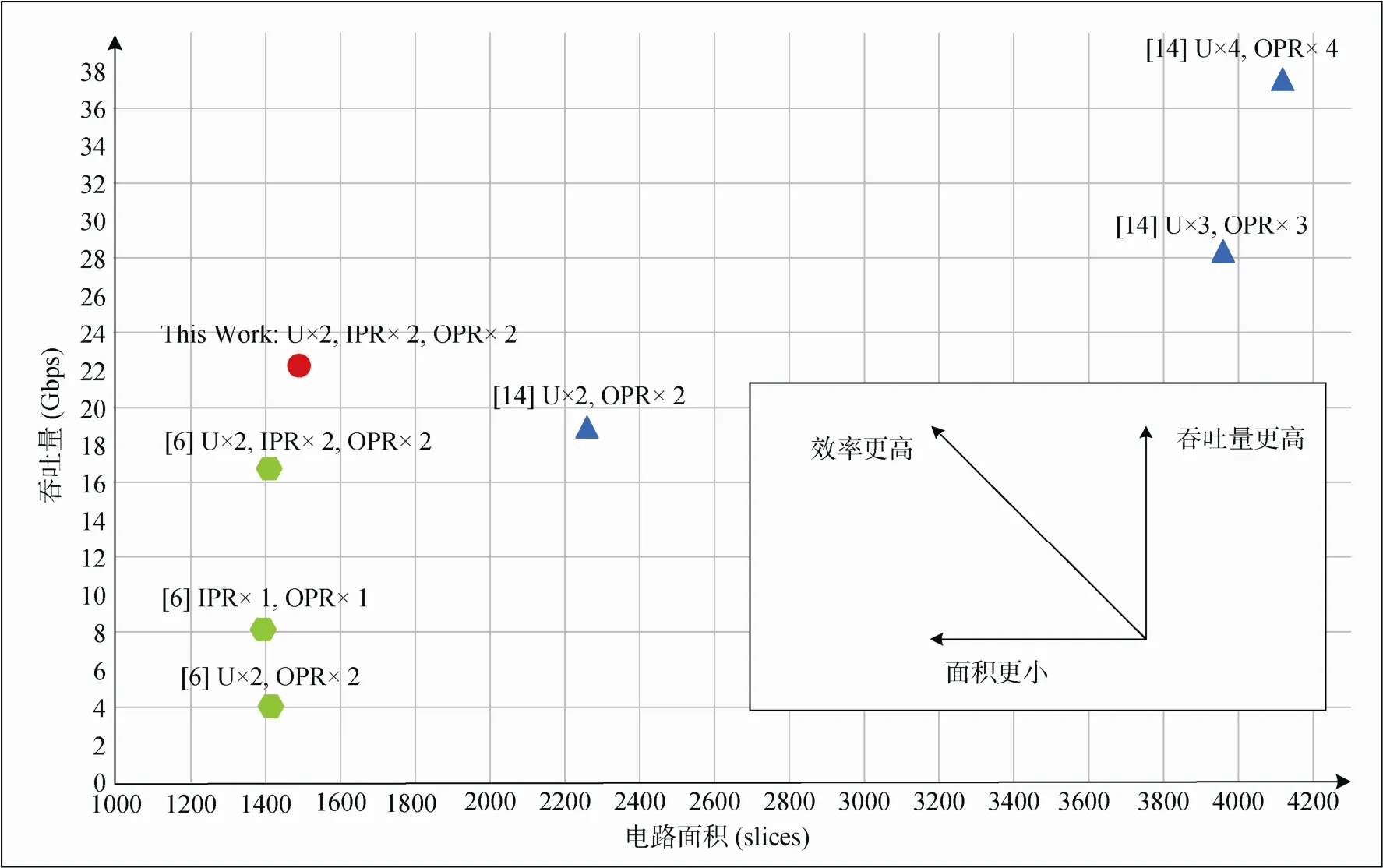
图5 与前人相关工作的比较(U=展开系数, IPR=内部流水线寄存器数量, OPR=输出流水线寄存器数量)Figure 5 Comparison of some previous works (U = the factor of unrolling, IPR = the number of inside pipeline registers, OPR = the number of output pipeline registers)

5 结论

本设计提出了一种应用于后量子密码的高速高效SHA-3硬件结构, 可显著提高运算速度和效率。本设计采用7-bits的简化轮常数代替64-bits的轮常数, 且通过改善流水线的结构来改善关键路径, 从而提升系统频率。同时, 本设计采用了二次展开的硬件结构, 并在运算过程中插入和每轮结束后插入流水线寄存器以提高效率。在Xilinx Virtex-6 FPGA上的验证表明, 本设计的最高工作频率为459MHz, 效率可达14.71 Mbps/Slice。与前人工作相比, 最高工作频率提高了10.9%, 平均效率提高了约28.2%。