基于EMD的短期风速预测混合模型

周学均，陈小强，谢磊，江成龙

（1.中电国际胡布发电有限公司,巴基斯坦 卡拉奇 74200；2.中电华创电力技术研究有限公司，江苏 苏州 215123；3.浙江大学 智能系统与控制研究所，浙江 杭州 310027）

在风速预测领域，研究人员提出了很多不同的预测模型去解决风速序列强非线性和强非平稳性的问题。机器学习和深度学习算法的快速发展，提供了有效拟合非线性和非平稳性的时间序列的工具[1]。在机器学习方法中，人工神经网络是最常用也是最有效的方法，由于人工神经网络的结构性，基于反向传播算法调整权值的神经网络(BPNN)是神经网络中用得最多的方法之一[2]。Z.H.Guo等[3]基于BP神经网络提出了一种风速预测模型，利用不同地区的风速资料进行实例验证，证明了所提方法的优越性。为了有效解决BP神经网络收敛速度慢、容易陷入局部最优值的问题，研究人员进行了大量研究。现阶段主要的解决方法仍然是遗传算法（Genetic Algorithm,GA）[4]或者灰狼算法(GWO)[5-6]等。王德明等[6]提出了基于BP神经网络的短期电场风速预测模型，采用遗传算法(GA)对BP神经网络的权值和偏差进行优化，应用优化后的BP神经网络对风速进行预测。实验结果表明，与BP神经网络相比，该方法具有精度高、收敛速度快等优点。

由于风速序列的间歇性、非平稳性以及差异性等特点，风速时间序列十分复杂，很多单一的模型并不能取得良好的预测效果，因此研究人员开始将预测方向转向混合模型，提出了将风速序列分解成一系列子序列的方法，被分解的每个单一子序列可单独分析预测，最后预测结果线性相加[7]。当今主流的信号分解方法仍然是围绕经验模态分解（Empirical Mode Decomposition,EMD）模型完成的。Z.H.Guo等[8]提出了一种基于经验模态分解的前馈神经网络模型（EMD-FNN）用于风速预测。首先利用EMD技术将非线性、非平稳的原始风速序列分解为有限个且数量较少的固有模态函数（Intrinsic Mode Function,IMF）和一个残差序列r，然后用模糊神经网络分别预测除高频以外的子序列，最后将模拟的IMFs和残差序列的预测结果进行综合，形成对原始风速序列的集合预测分析。通过实验验证，与基本模糊神经网络相比，该模型具有较好的预测精度[9]。

本文首先对风速预测单一模型自回归移动平均模型（ARIMA）、支持向量机（SVM）、BPNN、GABPNN进行对比，确定了预测精度最高的单一预测模型为GA-BPNN，然后介绍了经验模态分解算法，实现了基于EMD的简单混合预测模型EMDARIMA、EMD-BPNN、EMD-SVM以及EMD-GABPNN。实验表明，EMD-GA-BPNN的预测效果优于其他模型。

1 EMD算 法 和GA算 法

1.1 EMD算法

EMD是 由N.E.Huang等[10]于1998年提出的一种自适应分解算法，此算法无数学理论基础，完全是一种经验性的数据驱动算法，能有效处理非线性等复杂信号。与小波分解不同，EMD无需指定任何分解前参数包括基函数等，就可以达到很好的分解效果[11]。EMD的思想是将一组数据分解成有限的几个固有模态函数和一个残差序列r。分解的IMF需要满足两个条件：（1）在整段信号序列上，极值点和序列零点数量的差值不能超过1；（2）在任一点上，上下包络的均值必须为0。

令x(t)表示原始序列，具体的EMD分解步骤为：

（1）找到x(t)的所有极值点，包括极大值和极小值，通过三次样条插值法分别求出极大值和极小值的包络线xup(t)和xlow(t)。同时，计算上下包络线的平均值：

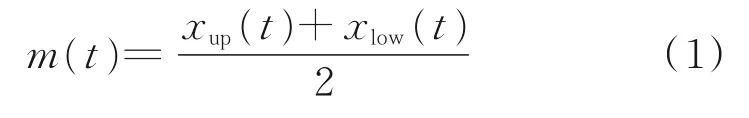
（2）将计算得到的包络线平均值m(t)从原始序列x(t)中减去得到原始序列的细节成分：

（3）核实d(t)是否满足成为IMF的两个条件，如果满足，那么令c(t)=d(t)，同时计算残差r(t)，并用r(t)代替计算原始序列x(t)：

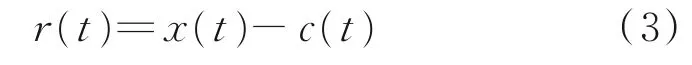
否则使用d(t)代替x(t)，并且不断重复步骤（1）和步骤（2），直到EMD分解终止条件被满足。

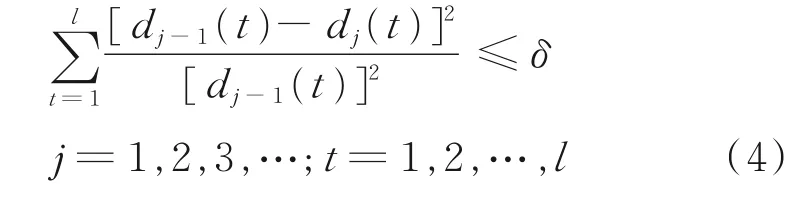
式中，l为序列的长度；j为迭代次 数，δ为迭代停止的最终阈值。一般将此过程称为IMF筛选过程。

（4）不断重复步骤（1）-（3），直到所有的IMF都被筛选出来，最后可以获得一系列的IMF和最后的残差。

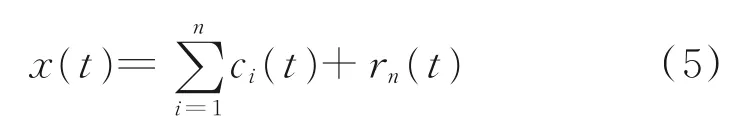
式中，ci(t)为分解的IMF，i=1,2,…,n；rn(t)为不满足分解要求的残差[12]。

EMD分解算法流程如图1所示。图中，h（t）、c（t）表示中间变量。

图1 EMD分解算法流程

1.2 GA算法

遗传算法是由J.H.Holland[13]提出的优化算法，该算法要根据生物学中的进化规律进行设计，是基于进化论中的自然选择和遗传学生物进化的计算模型，用来搜索最优解。遗传算法一开始会产生一组随机解，被称为种群，同时种群中拥有一些个体，这些个体为染色体。事先定义目标函数，用来计算和评价每一个染色体的适应度。在遗传算法的进化过程中，经过选择、交叉以及变异等操作，根据适应度不断更新染色体的存活情况，从而更新群体。不断重复上述进化过程，直到染色体满足一定的标准。其中，将求解的过程转化成生物进化中染色体基因的交叉变异的过程，能够获得良好的优化结果。遗传操作主要包含三个基础的遗传算子。遗传算法的流程如图2所示。图中，G表示当前进化代数；GEN表示最大进化代数。

图2 遗传算法流程

GA算法具体步骤为：

（1）初始化：设置进化数计数器t=0，设置最大进化代数T，随机生成M个个体作为初始种群P（0）。

（2）个体评价：计算种群P（t）中各个个体的适应度。

（3）选择运算：将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。

（4）交叉运算：将交叉运算子作用于群体，即对群体中个体串的某些基因座上的基因值做变动。群体P（t）经过选择、交叉、变异运算之后得到下一代群体P（t+1）。

（5）变异运算：将变异算子作用于群体，即对群体中个体串的某些基因座上的基因值作变动。群体P（t）经过选择、交叉、变异运算之后得到下一代群体P（t+1）。

（6）终止条件判断：若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出，终止计算[14-15]。

2 EMD-GA-BPNN短期风速预测模型

因为BP神经网络本身带有局限性，收敛速度差且容易陷入局部最优，因此本文加入遗传算法去优化BP神经网络的权值[16]。

GA-BPNN算法流程如图3所示。

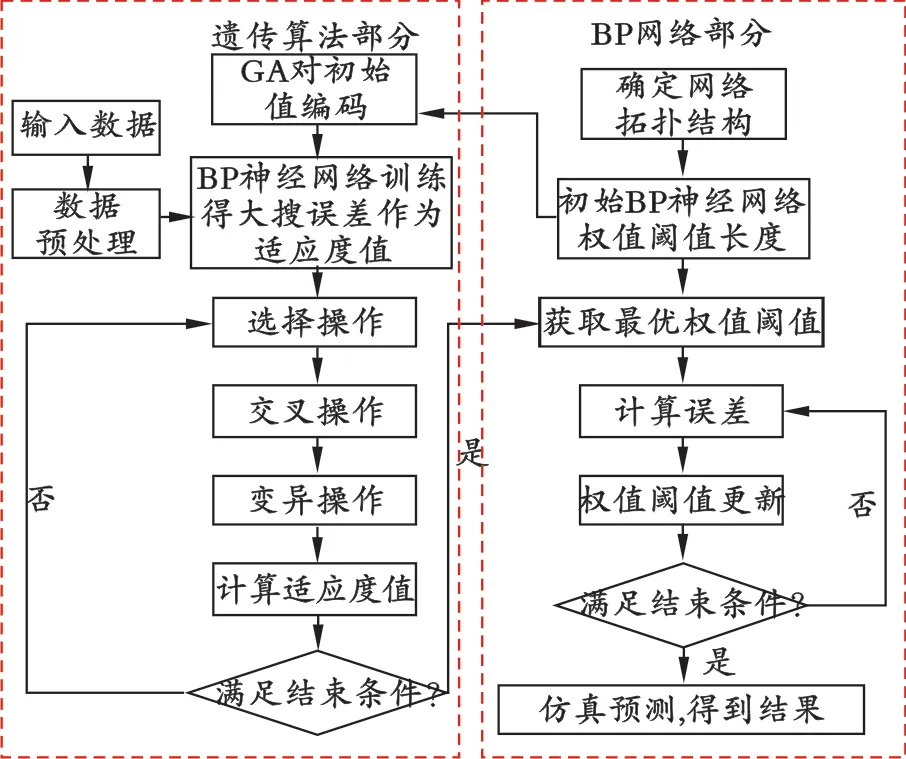
图3 GA-BPNN算法流程

GA-BPNN算法步骤为：

（1）首先进行个体编码。个体主要包括优化神经网络的权值和阈值，单一个体都是由实数串组成的，由神经网络的两部分连接权值以及隐含层阈值和输出层阈值四个部分组成。

（2）所优化的神经网络初始权值和阈值由个体确定，之后训练BP神经网络模型，将预测值和实际值的误差绝对值作为遗传算法的个体适应度F。

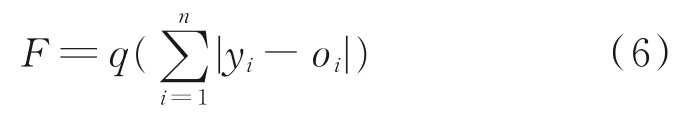
式中，n为网络输出节点数；yi为BP神经网络的第i个节点的期望输出；oi为第i个节点的预测输出；q为系数。

（3）选用轮盘赌法作为优化过程的选择操作的方法，即选择策略会根据适应度的相应比例，即每个个体i的选择概率pi进行调整。

式中，N为种群个体数目；fj为适应度比重；fi=k/Fi，其中Fi为节点i的适应度，适应度越大效果越差，因此求取适应度倒数，再进行个体选择。

（4）选用实数交叉法作为交叉操作的方法。那么第k个染色体ak和第s个染色体as在j位的交叉操作方法为：

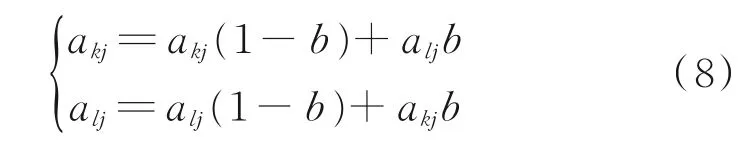
式中，b为[0,1]的随机数。

（5）选定第i个个体的第j个基因aij进行变异，变异的具体过程为：

式中，amax为基因aij的上界；amin为基因aij的下界；r为[0,1]的随 机 数；f(g)=r2(1-g/Gmax)2；r2为随机数；g为当前迭代次数；Gmax为最大进化次数。

在优化预测模块中加入EMD分解算法，EMDGA-BPNN算法流程如图4所示。

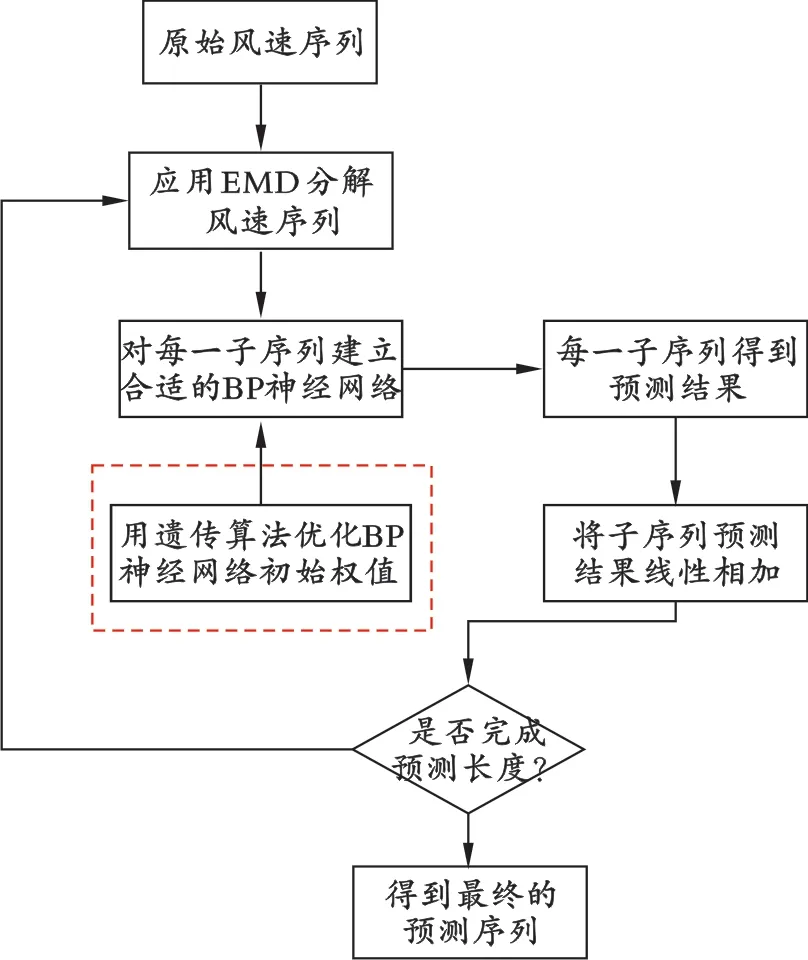
图4 EMD-GA-BPNN算法流程

EMD-GA-BPNN算法具体步骤为：

（1）给定历史风速原始序列x(t)，其长度为l，并且划分训练集长度ltrain和测试集长度ltest，将训练集长度的历史风速数据集进行EMD分解得到子序列x(1)ltrain,x(2)ltrain,…,x(m)ltrain，将每一子序列进行数据的预处理得到GA-BP神经网络的输入数据。

（2）构建GA-BP神经网络。初始化BP神经网络的初始权值和阈值，得到m个神经网络预测模型，对每一个网络进行训练并且预测得到预测结果

（4）判断预测值的长度是否等于测试集长度ltest，若是，则转入步骤（5），否则更新训练集长度ltrain=ltrain+1，重复步骤（1）-（3）。

（5）预测值长度达到测试集长度，算法结束。

3 实际案例

实验使用的风速数据集采集自国内3个不同的风电场，风速序列采样的时间间隔是1 h。实验用电脑的CPU为Intel i5-8265U、内存为8 GB DDR4、显卡为MX250、操作系统为64位Windows10，仿真软件为MATLAB R2019a。

3.1 评价指标

在风速预测领域，评价指标一般采用时间序列预测的评价指标[17-18]。

（1）平均绝对误差（Mean Absolute Error，MAE）：

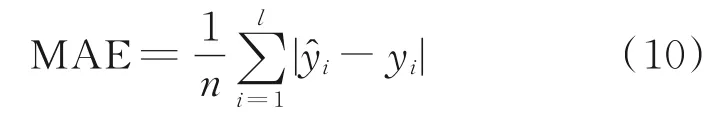
当此项指标为0时，代表预测值与真实值完全相同，即为完美模型。此项指标越大，则代表预测误差越大；此项指标越小，则代表预测结果越好，预测模型拥有越好的精度。

（2）平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）：

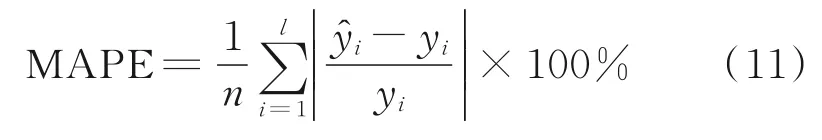
MAE预测值有时会很大，不能完全反映预测准确度，MAPE可以将预测的误差从具体数值转化成占原数据大小的百分比，可以更为直观地表示预测偏差。

（3）均方根误差（Root Mean Square Error，RMSE）：

RMSE为均方误差（Mean Square Error，MSE）的平方根，代表预测值的离散程度，也叫标准差。均方根误差越大，表示预测结果离散程度越大；均方根误差越小，表示预测结果与实际观测值的拟合程度越好。

3.2 案例分析

实验1为BPNN、SVM、ARIMA和GA-BPNN单一模型预测风速效果。实验模型参数如表1所示。

表1 实验模型参数

本文的数据集是一段短期风速数据集，是采集于河北省永盛庄风电场2015年的风速数据，时间是1月1日00:00至2月1日00:00，共 计744个 风 速 数据点，采样时间间隔为1 h。为了方便研究，将其中的500个点作为此次对比实验的数据，实验数据集如图5所示。将数据的80%共计400个点作为模型的训练集，剩下的20%共计100个点作为测试集，与预测结果进行对比从而表征预测效果。

图5 实验数据集

各模型预测值与原始数据如图6所示，各模型预测回归结果如图7所示，各模型预测残差如图8所示。各模型的预测误差性能指标如表2所示。

表2 各模型的预测误差性能指标

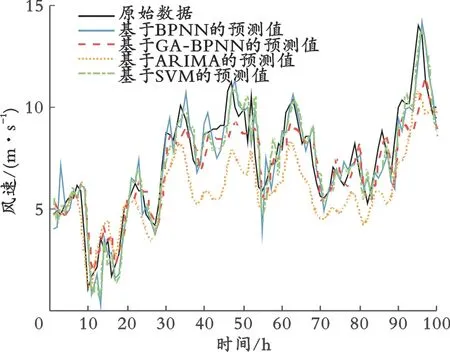
图6 各模型预测值与原始数据

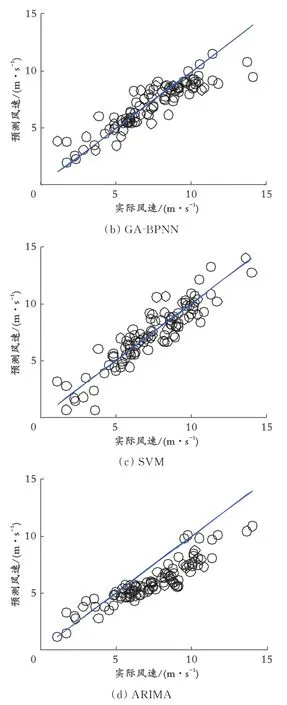
图7 各模型预测回归结果

图8 各模型预测残差

从表2和图6-8可以看出，GA-BPNN的预测效果比其他的单一模型预测效果更为优异。在所有对比的单一短期风速预测模型中，GA-BPNN的预测效果在各项指标中都是最佳的。因此，可以得出以下结论：

（1）对于风速这种非平稳和非线性的间歇性比较强的时间序列，传统的统计学模型预测很难达到预期效果，尽管能很好地预测风速数据的变化趋势，但是预测精度不够，尤其是在风速序列的一些极值点处。

（2）BP神经网络的各项指标优于SVM预测模型。在指标统计中，SVM的MAE为0.998 1，MAPE为16.91%，而BP神 经 网 络 的MAE只 有0.879 8，MAPE只有16.00%，而且考虑SVM和BP神经网络的模型结构，BP神经网络具有更强的适应性和更好的拟合效果。因此，考虑将BP神经网络作为需要优化的单一预测模型。

（3）经过初始权值优化的GA-BP神经网络预测模型的MAPE在此次实验中可以达到14.36%，预测效果比单一的BP神经网络提高了10.25%，而MAE也降低到0.806 4，相比SVM预测模型降低了0.191 7，相比BP神经网络降低了0.073 4，实现了预测效果大幅度的提升。不管是哪种模型，在风速数据的极值点处的预测误差都会变大，甚至预测效果最好的模型在峰值处反而预测误差最大，因为风速特性的问题，单一预测模型无法克服由于极值点的强非线性带来的预测误差问题。因此，研究人员将风速预测的模型逐渐转向基于时频分解的数据预处理混合预测模型进行研究。

实 验2为EMD-BPNN、EMD-SVM、EMDARIMA和EMD-GA-BPNN混合模型的风速预测效果。使用与实验1相同的原始数据。

实验数据EMD分解如图9所示。各预测模型参数如表3所示。

图9 实验数据EMD分解

表3 各预测模型参数

从图9可以看出，随着分解的进行，分解的IMF的频率会逐渐降低，且共分解出7个模态。第1个IMF频率最高，振荡较大，代表风速数据的噪声部分，最后一项既平滑又平稳，代表风速数据的趋势部分。由图9还可以看出，原始的非线性非平稳的风速信号被EMD分解成一系列拥有一定规律和特征的信号分量。

使 用EMD-ARIMA、EMD-SVM、EMDBPNN、EMD-GA-BPNN 4种模型，对EMD分解的平缓子序列进行预测，将每个子序列的预测结果进行线性组合，得到最终的预测结果。EMD分解的各模型预测值与原始数据如图10所示，EMD分解的各模型预测回归结果如图11所示，EMD分解的各模型预测残差如图12所示，EMD分解的各模型预测误差性能指标如表4所示。

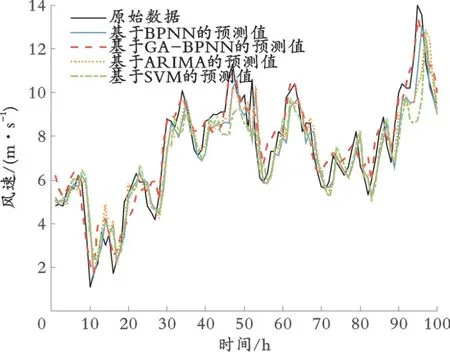
图10 EMD分解的各模型预测值与原始数据

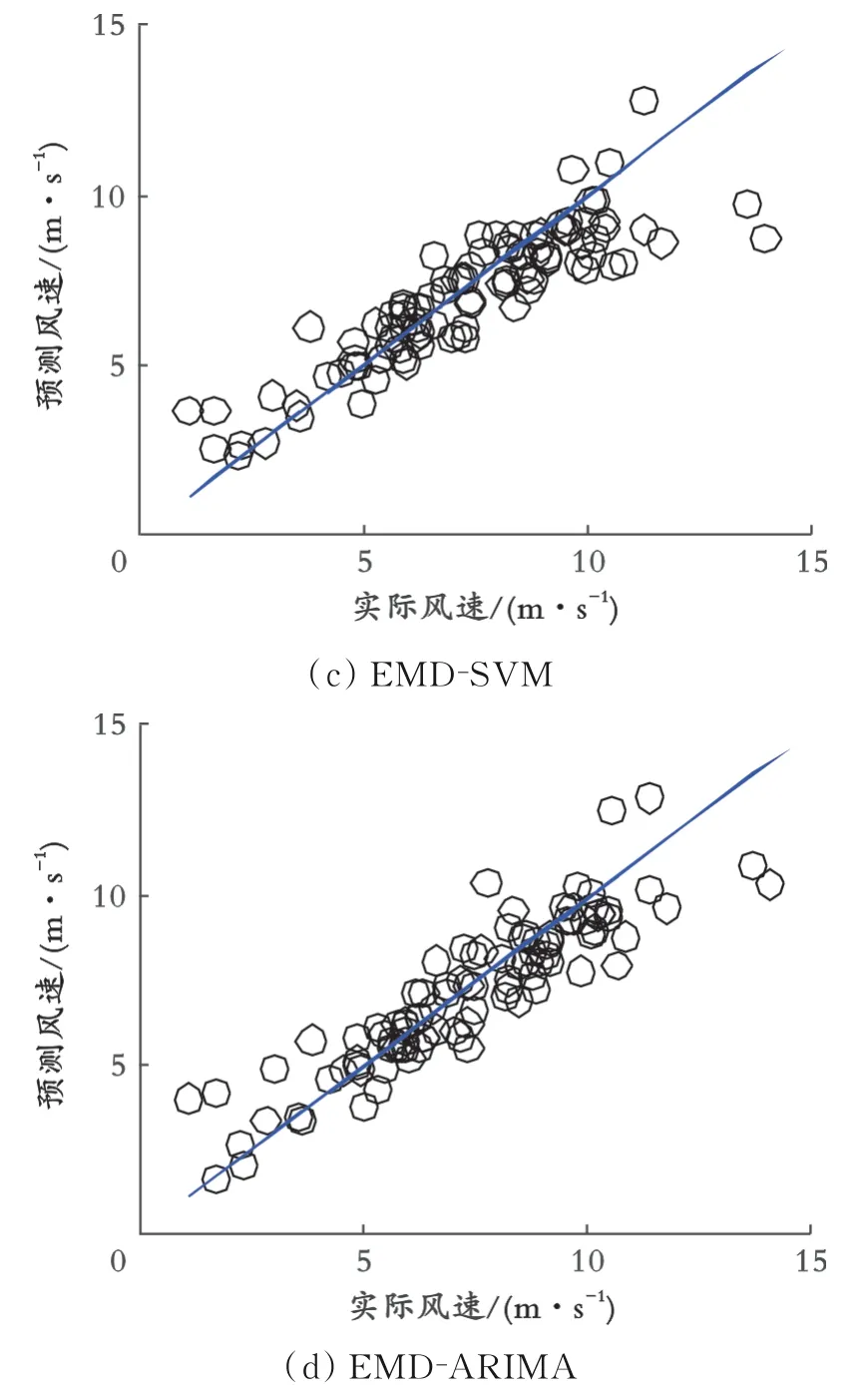
图11 EMD分解的各模型预测回归结果

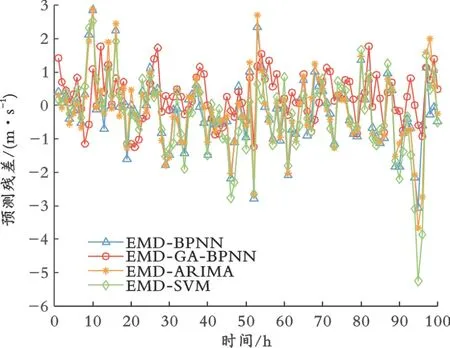
图12 EMD分解的各模型预测残差

表4 EMD分解的各模型预测误差性能指标

因为实验2的数据集和实验1的数据集完全一致，所以只在预测误差统计指标的表格中加入了GA-BPNN神经网络在实验1中的预测结果。从表4和 图10-12可 以 看 出,EMD-GA-BPNN模 型 较 其他模型在短期风速预测领域具有最好的预测效果。

对比实验2与实验1可以看出，基于EMD的混合预测模型EMD-ARIMA、EMD-SVM、EMDBPNN均可以提高风速预测准确度，降低风速预测的平均误差，其中预测效果提升幅度最大的是EMD-ARIMA，其预测精度接近EMD-SVM。这说明分解后的子序列极大地降低了风速序列中的间歇性、非线性以及非平稳的特征，ARIMA可以很好地拟合分解后的子序列，提升最终的预测结果。另外，混合模型的预测准确度与单一模型的预测准确度相关，单一模型的选择会影响混合模型的预测精度。

对比结果还可以看出，EMD-GA-BPNN的预测效果优于EMD-ARIMA、EMD-SVM、EMDBPNN，其预测残差约为0，而EMD-SVM的预测残差在原始风速的极值处发散，其他混合预测模型也会出现同样的问题。由此可知，与其他混合预测模型相比，EMD-GA-BPNN具有较强的预测稳定性和鲁棒性。

4 结论

（1）实验1对比了单一的预测模型和加入遗传算法的GA-BP神经网络模型。结果表明，遗传算法GA的加入提升了BP神经网络预测模型的预测准确度。

（2）实验2对比了4种混合预测模型。结果表明，基于优化算法和时频分解的短期风速混合预测模型在实际应用中具有巨大潜力。