一种集装箱港口复杂网络构建方法

刘渊哲， 韩 懿， 王新波，3

(1. 上海船舶运输科学研究所， 上海 200135； 2. 中远海运科技股份有限公司， 上海 200135；3. 上海交通大学 船舶海洋与建筑工程学院， 上海 200240)

0 引 言

根据联合国贸易与发展会议发布的《2020全球海运发展评述报告》，2020年全球集装箱船队的总运力为2.7亿载重吨，占全球海运贸易量的13.1%[1]，在全球贸易中扮演着不可替代的角色。北京时间2021年3月23日02：00至3月29日05：00，长荣海运的“长赐号”集装箱船搁浅，导致苏伊士运河双向堵塞断航，引发了严重的运河通航中断事故，产生了巨大的经济损失[2]。在大多数航运及港口复杂网络研究中，有关苏伊士运河各项指标的排名均未体现出与此次事件相匹配的重要性。例如，徐梦俏[3]和关晓光等[4]基于节点中心性对集装箱港口的重要性进行评价，苏伊士运河各项指标的排名均未进入前20位。本文以苏伊士运河堵塞事件为例，基于船舶自动识别系统(Automatic Identification System，AIS)数据构建L空间集装箱港口有向加权复杂网络，研究不同网络构建方法、不同权重和不同周期下苏伊士运河各项网络指标的表现，构建更贴近实际运营规律的集装箱港口复杂网络。

1 研究现状

复杂网络是对复杂系统的抽象描述，将系统的组成单元抽象为节点，将各单元间的相互关系抽象为边，研究网络拓扑结构和动力学行为，已广泛应用于交通类网络研究中。目前，集装箱港口网络的构建模式主要有P空间模型和L空间模型2种，其中：P空间模型规定同一条航线上的所有节点都两两相连；L空间模型规定仅相邻的2个节点才存在连接关系。研究发现，在数据相同的情况下，采用L空间模型构建与P空间模型构建的集装箱航运网络的特征有一定的差异[5]，其中：L空间有利于考察节点间的距离和空间约束[6]，适于研究港口在网络中的空间特性；P空间能更好地反映港口间连接性的强弱[7]，适于研究船舶中转情况[8-9]。这2种网络构建模式在不同的研究场景下具有不同的应用领域。

集装箱港口网络的权重选择和连接方式也存在多种模式[10-12]。

1) 权重选择有航次和标准箱数量2种方法，其中以标准箱数量为权重构建网络的研究相对较少，这与船舶舱位登记信息难以获取有关。

2) 在连接方式中：无向无权网络多见于初期研究和网络层次体系研究[13-15]中；无向有权网络多见于注重港口流量特征的研究[16-17]中；有向无权网络不常见；有向有权网络更贴合实际运营情景，在拓扑结构和流量处理方面具有更好的可描述性[18]。

目前，在集装箱港口网络研究中，网络构建和数据处理还存在一定的不足，导致大多数网络条件下的苏伊士运河指标排名与实际情况不匹配，具体表现在以下几个方面：

1) 采用P空间模型构建集装箱港口网络，未考虑航线分离问题；

2) 采用集装箱船航线船期表作为数据源，与实际网络连接情况存在一定的偏差；

3) 网络以航次为权重，不足以描述集装箱船在航线上的真实运力分布情况；

4) 在数据时间选取上，以往的港口复杂网络理论研究往往以年为统计时长单位，统计周期较长，即在静态网络背景下对港口网络连通现状进行研究，不具有时变性。

2 研究方法

本文基于船舶AIS动态数据和埃信华迈(IHS Markit)公司海事与贸易司提供的船舶档案构建集装箱港口网络。以港口为节点，以集装箱船历史挂靠港为连接边，分别以航次和船舶标准箱数量为边权，构建2020年L空间有向加权港口网络。同时，以出入节点强度、出入度接近中心性和中介中心性为指标，以苏伊士运河各项指标的排名表现为指示，对本文提出的网络构建方法的有效性进行验证，即验证苏伊士运河港口在实际集装箱船运营中的重要性是否在网络指标的排名中得到了体现。此外，以日为单位提取2020年3月15日至2020年4月5日的运河通行数据，建立21 d的逐日动态网络，观察短期堵塞情境下各项指标的变化情况，对港口拥堵的动态特征进行探究。

2.1 网络构建方法

2.1.1 网络权重选取

集装箱港口网络加权方式有2种：一种是以港口节点间连接频率为权重，即航次加权；另一种是以连接2个节点航线的船舶舱位数量为权重，即标准箱数量加权。本文分别采用航次和标准箱数量作为网络连接权重进行网络指标排名对比，对不同权重下的网络特征差异进行观察。

2.1.2 网络连接数据处理

由于未出现在船期表上的记录的连接常常会被漏取，易造成运河港口节点的网络指标与实际偏离。由此，对运河港口出入连接航段的数据进行处理，主要包括2步：

1) 将以该港为航段起始港或到达港的航段计入连接中；

2) 对仅通过运河的航段进行分解，根据航段经过的关键航道节点信息筛选起止港均非运河港，但航迹穿越运河航道节点的航段，拆解为2个航段计入网络中。

2.1.3 网络空间模型

将目前常用的2种航运网络构建模式与实际航线连接相对应，其中P空间模型认为同一航线上的所有港口之间都可进行贸易往来，不同航线上的港口不具有全连通特性，故在应用P空间模型时需获得航线数据和港口装卸箱数据。以5 668 TEU集装箱船“新宁波”近一年实际运营的航线为例，实际挂靠航线多表现为多个航线轮套，单一航线的界定和分离是建立P空间模型时存在的主要问题。因此，本文选择L空间模型构建网络，即存在直接挂靠关系的港口节点才存在连接关系。

2.2 网络节点重要性分析指标

在复杂网络中，节点度为直接连接的节点个数。BARRAT等[20]将节点度推广为加权网络中的节点强度，得到了广泛应用[21-24]。本文采用节点强度对港口进出口贸易量进行表征。

1)节点强度定义为与节点相连接的所有边权值的和，即

(1)

式(1)中，Si为节点强度；Ni为与节点i直接相连的节点集合；wij为边权值。有向网络中的节点强度分为出节点强度和入节点强度，在不同网络中采用相对节点强度对港口排名进行比较，有

(2)

2) 加权接近中心性(Weighted Closeness Centrality，WCCi)用于衡量该节点与其他节点的可达性和联通效率，与其他所有点的加权最短距离之和越小，接近中心性越强。

(3)

式(3)中，dij，w为节点i与节点j之间的加权最短路径长度。有向网络分为出接近中心性和入接近中心性。集装箱港口之间标准箱数量权重越大，贸易联系越紧密，故本文采用边权倒数计算节点间加权最短路径长度。

3) 加权中介中心性(Weighted Betweenness Centrality，WBCi)反映该节点对网络整体连通性的重要程度，即节点对网络中沿最短路径传输的网络流的控制力。网络中节点对加权最短路径通过该节点的数量越多，中介中心性越强。

(4)

式(4)中：nkj为节点k与节点j之间的加权最短路径数量和；nkj(i) 为节点k与节点j之间的加权最短路径经过节点i的次数[4]。

3 不同网络构建方法比较

本文以节点强度、中介中心性和接近中心性为指标，以苏伊士运河及部分具有代表性的港口在指标排名中的表现为指示，结合实际集装箱贸易情况，对采用不同方法构建的网络进行比较和评价，对本文提出的网络构建方法的有效性进行验证，并利用该方法构建逐日动态网络，对苏伊士运河的排名变化情况进行表征。

3.1 静态网络构建

选取2020年1月1日至2021年1月1日集装箱船已完成航段的数据和航线标准箱数据，去除加油挂靠与维修挂靠的航线连接，构建集装箱港口有向加权静态网络。该网络由1 063个港口节点和5 306艘集装箱船已完成的227 254个航段构成的10 287条连接线组成，涉及8.34亿TEU集装箱流动。

3.2 静态网络指标排名结果

1) 未增加分解航段处理的普通网络。航次权重和标准箱数量权重普通有向网络中心性排名分别见表1和表2。

表1 航次权重普通有向网络中心性排名

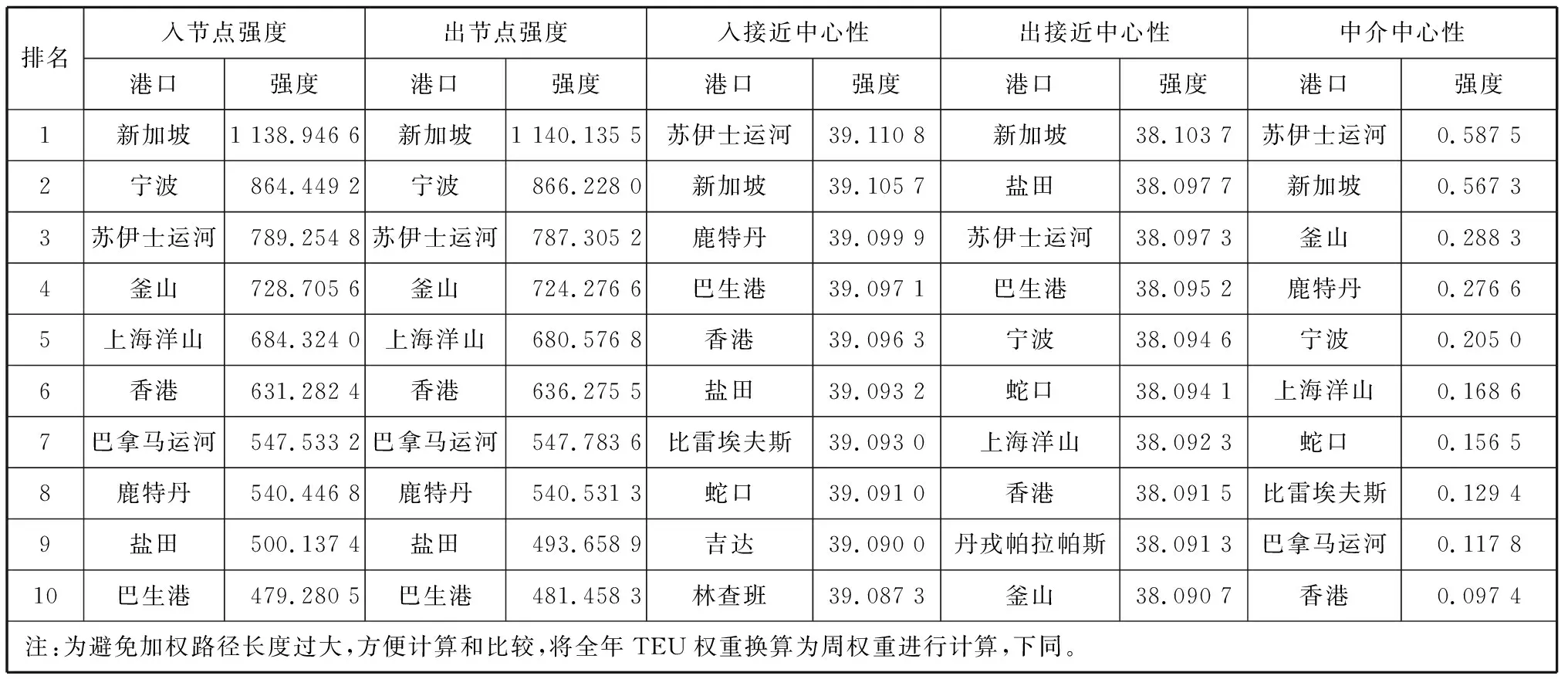
表2 标准箱数量权重普通有向网络中心性排名

2) 增加分解航段处理的提升网络。航次权重和标准箱数量权重提升有向网络中心性排名分别见表3和表4。

由表1～表4可知：

1) 在相同网络下，相比在航次权重网络中的排名，苏伊士运河和巴拿马运河的出入节点强度在标准箱数量权重网络中的排名更靠前。接近中心性和中介中心性指标注重研究网络节点间的连通性，新加坡港、苏伊士运河和鹿特丹港在2种权重网络中的接近中心性和中介中心性排名均有较好的表现，说明这些港口和运河在航运物流中转和地理位置方面都属于核心节点。同时可发现，新加坡港和青岛港的出入节点强度的排名上升，而上海外高桥港、香港港和高雄港的出入节点强度的排名下降，原因是实际航线中存在航次多而标准箱流动量少的现象，故相较于航次权重网络，以标准箱数量为权重的港口网络更能真实地体现集装箱在整个港口货物贸易流通网络中的重要性和在全球集装箱运力流动中的枢纽地位，可减少小型船舶频繁挂靠导致港口的中心性表现虚高的情况，更加贴近集装箱实际贸易流量情况。

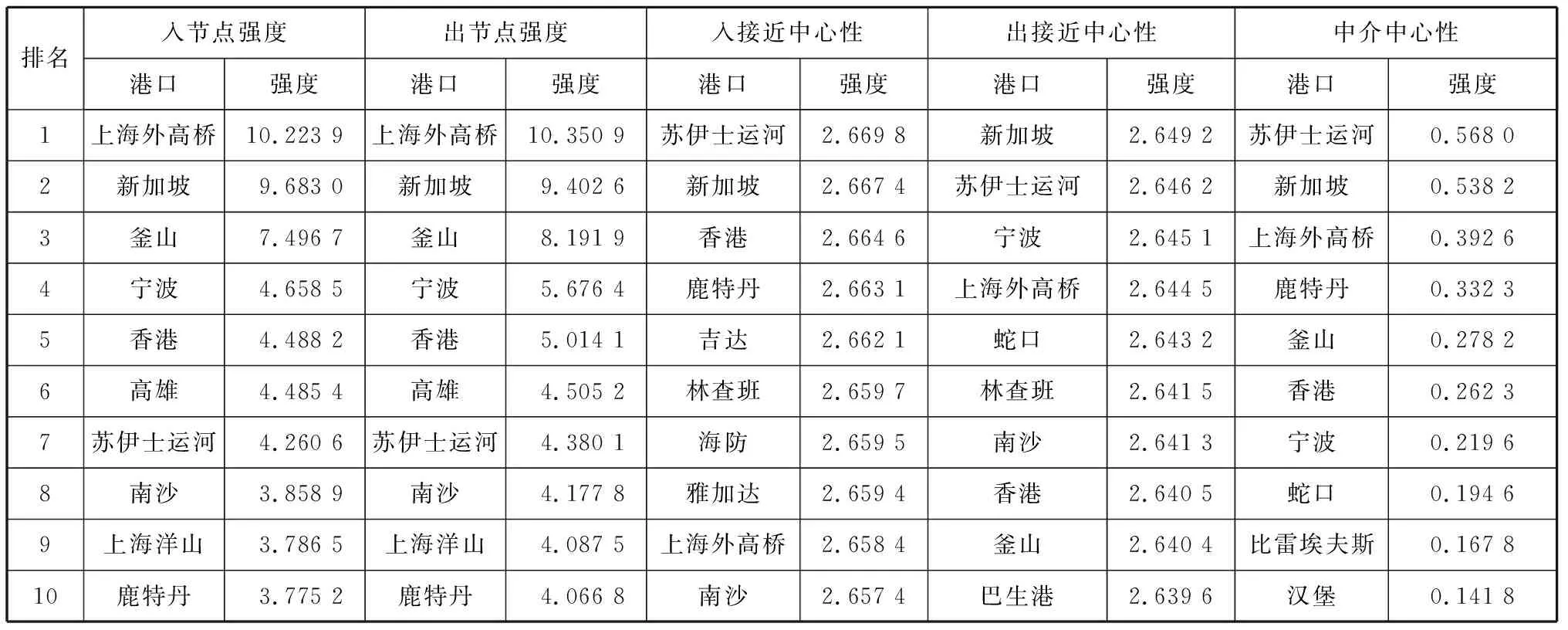
表3 航次权重提升有向网络中心性排名

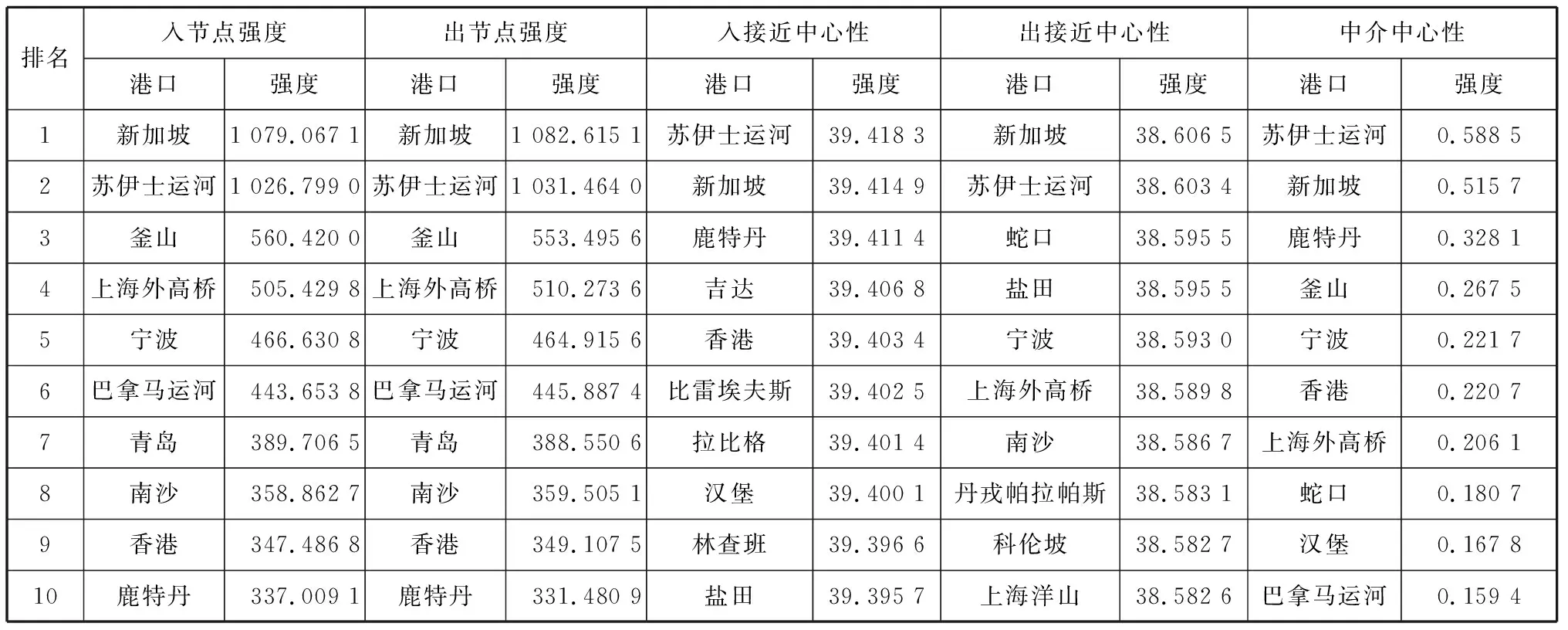
表4 标准箱数量权重提升有向网络中心性排名

2) 在相同权重下，在增加分解航段处理的提升网络中，苏伊士各项指标的排名在平均表现方面有一定的提升，航段分解使得苏伊士运河的连接贸易量增加，出入节点强度的排名提升；同时，苏伊士运河港口连接数量增加，使得其接近中心性的排名和中介中心性都有所提高，符合其承担全球12%航运货运量的情况。从各项指标排名前十的港口来看，巴拿马运河的排名也有一定程度的上升，故在对关键航道节点的重要性进行研究时，明确穿过航道即增加连接的原则具有一定的优良性，对通过航道的航线进行分解，还原该航道实际连接数据。

3) 在相同网络和相同权重下，各港口入节点强度的排名与出节点强度的排名一致，符合实际港口贸易中充分长的时间段内进出量平衡的情况；部分港口的节点强度排名未进入前十，而其接近中心性的排名有较好的表现，说明这些港口具有较高的节点度，连通性好，标准箱数量或航次周转次数多，贸易总量相对较少，为局部枢纽港，例如比雷埃夫斯港、吉达港和高雄港。一些港口的节点强度的排名表现优于接近中心性，表明这些港口虽然货运处理量比较大，但在全球集装箱运输网络中节点的支配能力较弱，如釜山港、青岛港；同时，同一港口的出入指标排名具有差异性，说明该港口在进出口贸易结构上具有不平衡性，符合不同港口在功能上具有一定倾向性的特征。

由以上分析可知，本文提出的集装箱港口网络构建方法具有一定的有效性，采用该方法构建的网络比较贴近航运实际情况。

3.3 动态网络构建与指标选取

利用以上建议网络的网络指标对港口堵塞后的网络动态演化特征进行表示，提取2021年3月15日至2021年4月5日的全球集装箱船航段数据和标准箱流动信息，构建逐日有向加权港口动态网络。对于集装箱港口网络来说，完成航段耗费的时间较长，24 h内形成的网络结构仅是整个网络的一部分，而网络节点的接近中心性和中介中心性侧重于描述网络拓扑结构的连通性，故在对运河堵塞期间的集装箱港口逐日动态网络进行研究时，主要以港口当日出入连接量为研究对象。

3.4 苏伊士运河动态网络指标排名结果

苏伊士运河出入节点强度排名见表5；苏伊士运河出入节点强度排名变化对比折线图见图1。

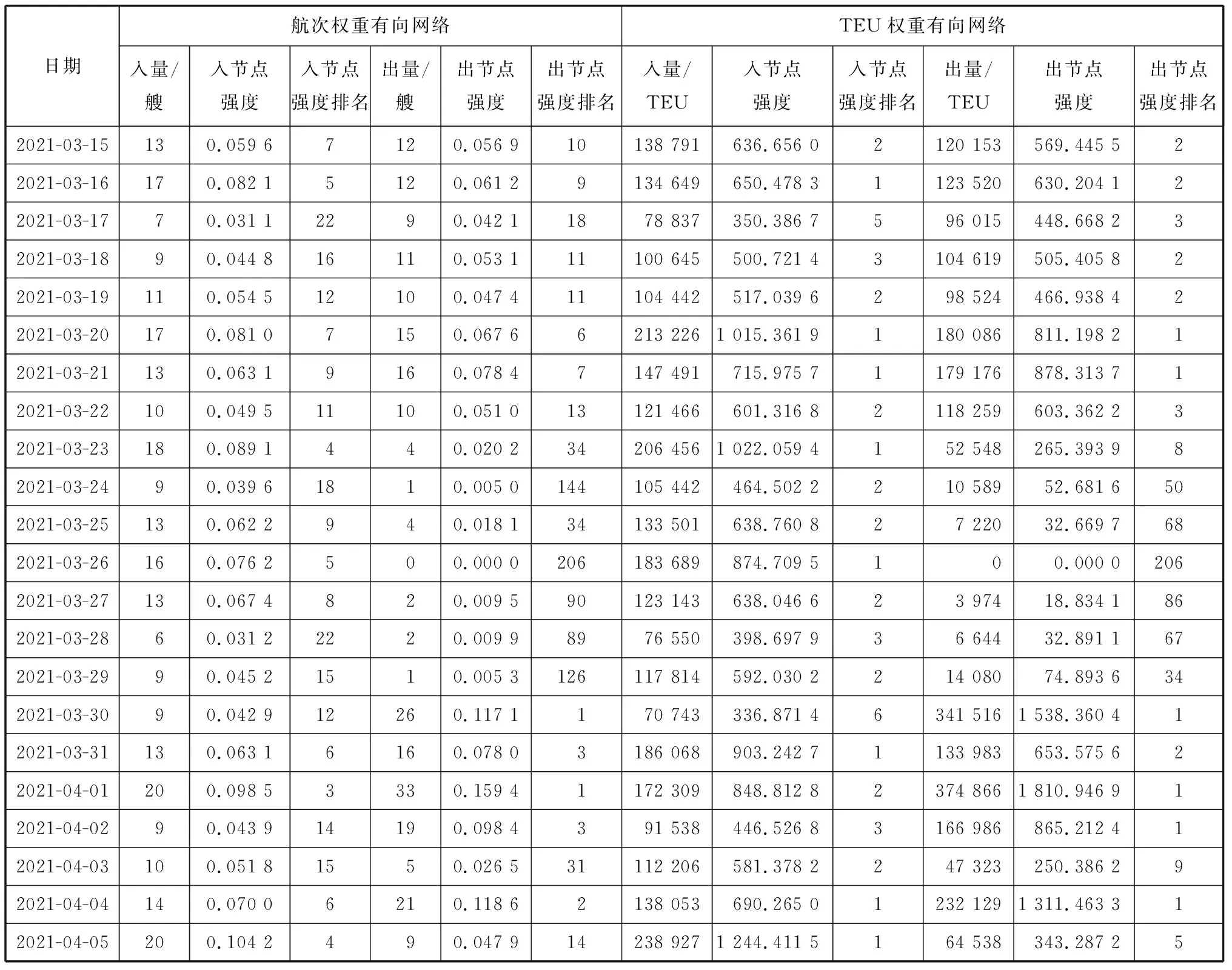
表5 苏伊士运河出入节点强度排名

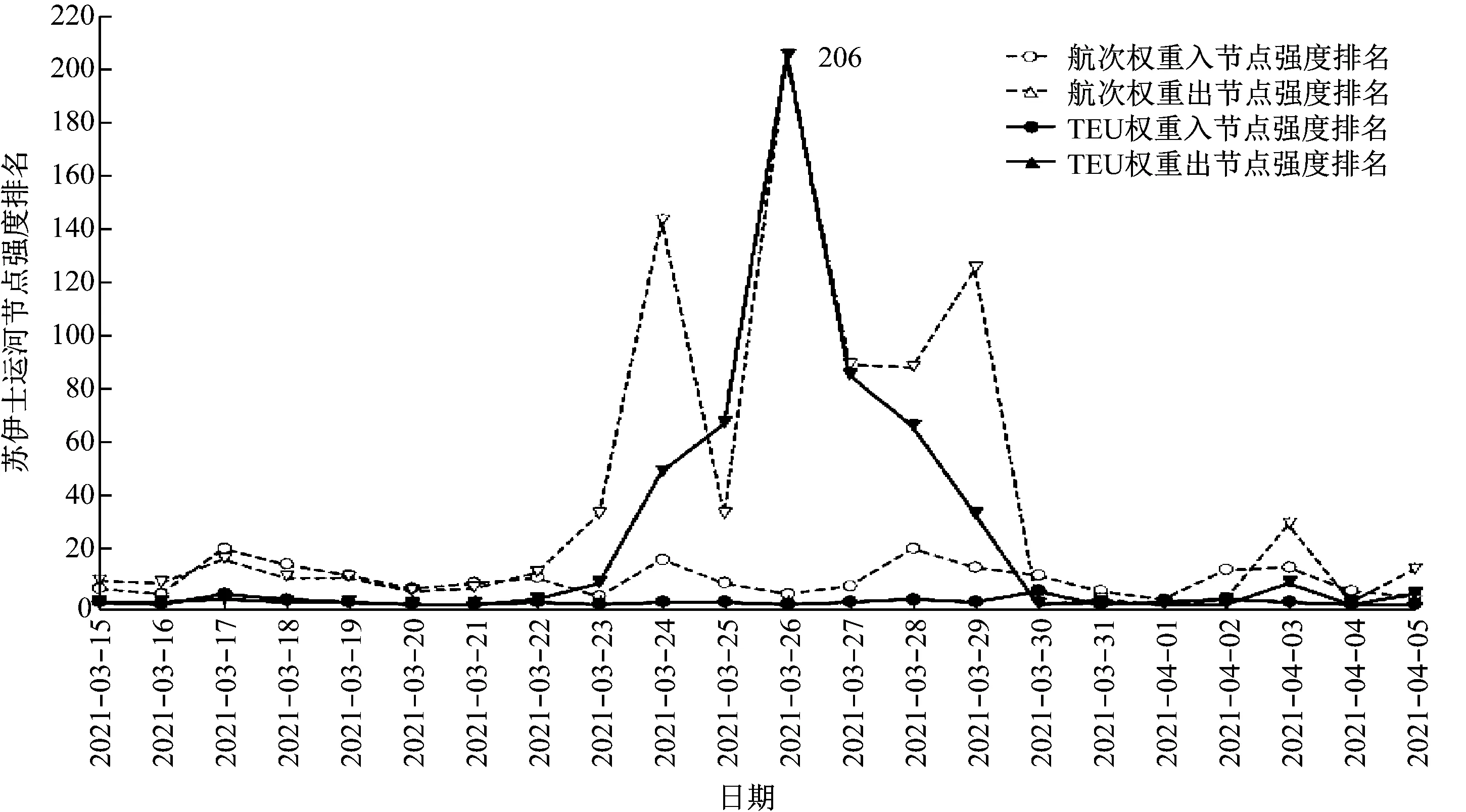
图1 苏伊士运河出入节点强度排名变化对比折线图

2021年3月24日起，驶入苏尹士运河的集装箱船的标准箱数量与正常通航时无较大差异(如图1所示)。对引发该现象的主要原因进行探究发现，运河断航之后，作为通往欧洲的替代航线，绕行南非好望角会使单程的航行里程额外增加3 000～7 000 n mile，船期延长1周以上，大型集装箱船的燃料成本会额外增加约48万美元，运营成本大大增加使得大部分船舶对改变航线持观望态度[25]。对于大部分船舶来说，短期等待产生的损失远少于绕航增加的成本，故多数船舶在获知堵塞信息之后仍选择航行至苏伊士运河附近等待通航，这表明苏伊士运河在欧亚航线上具有重要地位。

苏伊士运河堵塞期间，由于少量在地中海航行的小型集装箱船依旧保持正常通航，故苏伊士运河存在一定的集装箱船出量，但标准箱出量迅速减少(如表5所示)。2021年3月24日，苏伊士运河的出节点强度的排名由第八位下落至第五十位；2021年3月26日，苏伊士运河的集装箱船出量为0，出节点强度的排名降至最后一位；2021年3月29日，苏伊士运河滞留集装箱船达74艘，滞留集装箱量达到87.4万TEU(见图2)；2021年3月30日恢复通航之后，苏伊士运河的集装箱船出量和标准箱出量激增到第一位，此后均保持较高水平的出量。

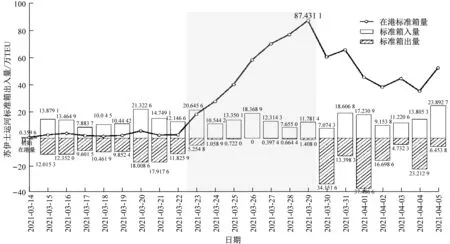
图2 苏伊士运河出入量变化对比折线图

综上，苏伊士运河堵塞期间，港口集装箱船入量保持正常水平，出量减少，短期堵塞不会导致船舶马上选择改线绕行，指标变化符合大部分船舶为降低运营成本，在短期内不改变既定航线的实际情况，说明在本文提出的网络中，利用节点强度指标的排名变化描述港口的实时动态具有一定的可靠性。

4 结 语

本文通过构建L空间全球集装箱港口有向加权复杂网络，在不同权重和数据处理方式下构建集装箱港口网络，根据苏伊士运河在网络中的节点中心性指标的排名表现对各网络进行比较，对本文提出的网络构建方法进行验证，并在采用该方法构建的动态网络中利用节点强度排名对苏伊士运河短期堵塞事件中船舶的靠离特征进行探究，主要得到以下结论：

1) 集装箱网络中标准箱数量权重相比航次权重更能表征港口间贸易量，更符合航线上实际货物流动情况。在构建港口贸易网络时，基于穿越运河港口即挂靠的原则，可避免遗漏关键航道连通数据，造成运河和海峡类港口的网络重要性指标与业务实际不匹配。构建P空间模型港口复杂网络的难点在于航线的分离和装卸箱量的采集，这些内容还需进一步探究。因此，本文建议构建L空间有向标准箱数量权重网络，对穿越运河港口的连接进行识别并增加挂靠动作。

2) 基于本文所述方法构建逐日动态网络，由出入节点强度排名的变化情况可知，苏伊士运河短期堵塞期间，港口入量几乎未出现波动，而港口出量出现剧烈下滑，导致在港船舶数和货物滞留量飙升，直到通航之后才有所缓解。这说明，考虑到运营成本和货物目标流向等多种因素，堵塞事件发生初期，船舶不会改变计划航线，是否可采用出入节点强度替换目前使用的港口绝对锚泊数量作为港口堵塞指标，有待进一步研究。

经静态网络指标和动态网络指标表现验证，本文提出的网络构建方法具有一定的可行性，采用该方法所得结果符合各港口在实际航运贸易中的功能特征和地位。