基于国产芯片的水声信号滤波器设计
石春华, 李 贺
(上海船舶运输科学研究所 舰船自动化事业部, 上海 200135)
0 引 言
在水声接收机中,一般要求带通滤波器在-3 dB频带内的频率响应比较平坦,保证具有一定大小的矩形系数。带通滤波器通常由多个二阶有源滤波器级联构成,当前采用国外先进的设计软件和专用的集成芯片可轻松地完成对此类电路的设计,且实用效果好,集成度高。相对而言,目前国内尚无合适的水声信号滤波器专用芯片。对此,为实现水声信号滤波器的自主可控,本文采用国产的运算放大器搭建一个八阶带通滤波器电路,通过查表和理论计算确定各二阶单元的中心频率、品质因数和增益,在此基础上进行设备选型和外围器件参数设计,并结合实际应用要求选择合适的电路形式进行仿真和测试。同时,制作多个通道评估该方案下各电路的一致性,根据实测的数据验证该设计方案的可行性。
1 带通滤波器传递函数
低通滤波器传递函数是所有滤波器的设计基础,二阶低通滤波器S域通用传递函数为
(1)
式(1)中:a1和b1为滤波器系数;A0为中频增益的模。由滤波器系数表[1]可知,当a1=1,b1=0时,二阶低通传递函数能演变成一阶低通传递函数,即
(2)

(3)
(4)
式(4)即为通用的二阶带通滤波传递函数,其中:Am为中心频率处增益;Q为品质因数。

(5)
2 各二阶单元带通滤波器f0和Q指标的确定
在某水声接收机的设计中,要求滤波器在通频带内的频率响应比较平坦,最大增益接近0 dB,噪声较小,因此采用巴特沃斯型的带通滤波器设计。
带通滤波器的指标如下:
1) 中心频率f0为80(1±1%) kHz;
2) -3 dB带宽BW为36(1±10%) kHz;
3) 矩形系数Kv(-40 dB/-3 dB)≤4;
4) 滤波器阶数为8阶;
5) 滤波器类型为巴特沃斯型;
6) 带内增益为0 dB。
在设计带通滤波器时,若 -3 dB上频点fH与下频点fL呈大于4倍频的关系,则需采用高通级联低通的形式设计,这属于宽带通滤波器设计。本文所述滤波器属于窄带通滤波器,采用4个二阶单元的窄带通级联达到设计目的。
1) 要设计八阶带通滤波器,需得到4组二阶单元的中心频率fmi和品质因数Qi,虽然难以直接定义各二阶单元的指标,但可先将八阶带通滤波器看成是由2个四阶带通滤波器级联得到的,根据八阶带通滤波器的设计指标预定义2个四阶带通滤波器的设计指标,具体见表1。

表1 预定义的2个四阶带通滤波器的设计指标
另外,BW1的取值范围可根据经验公式得到,有
(6)
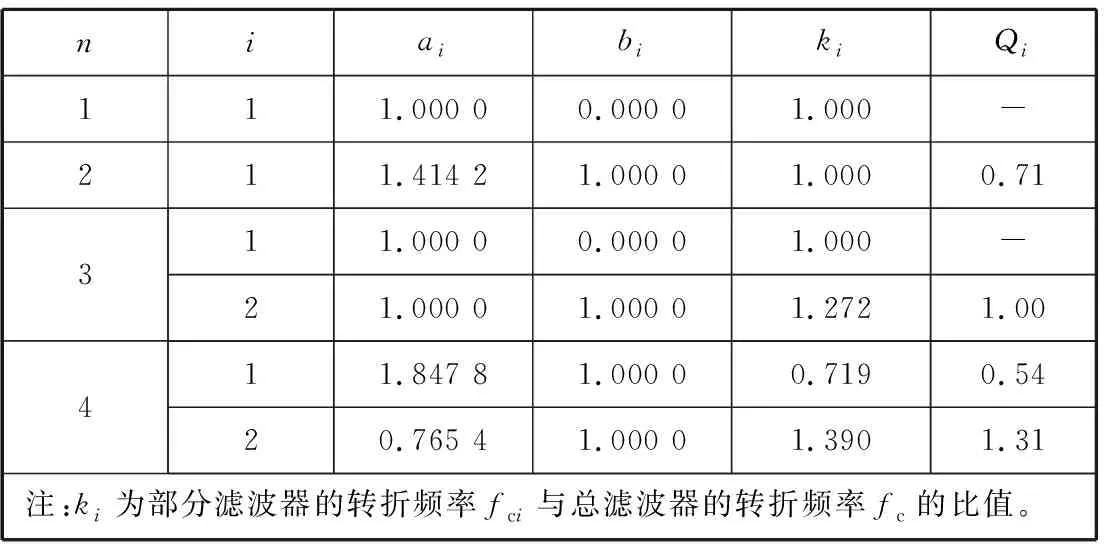
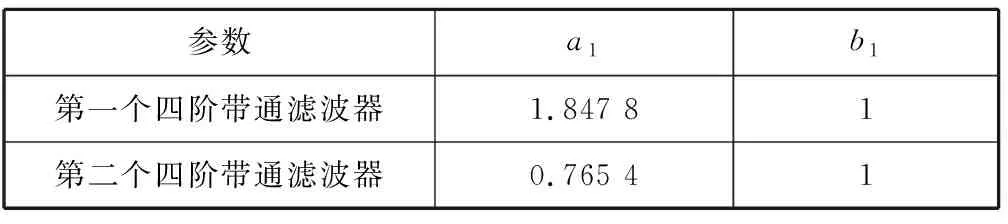
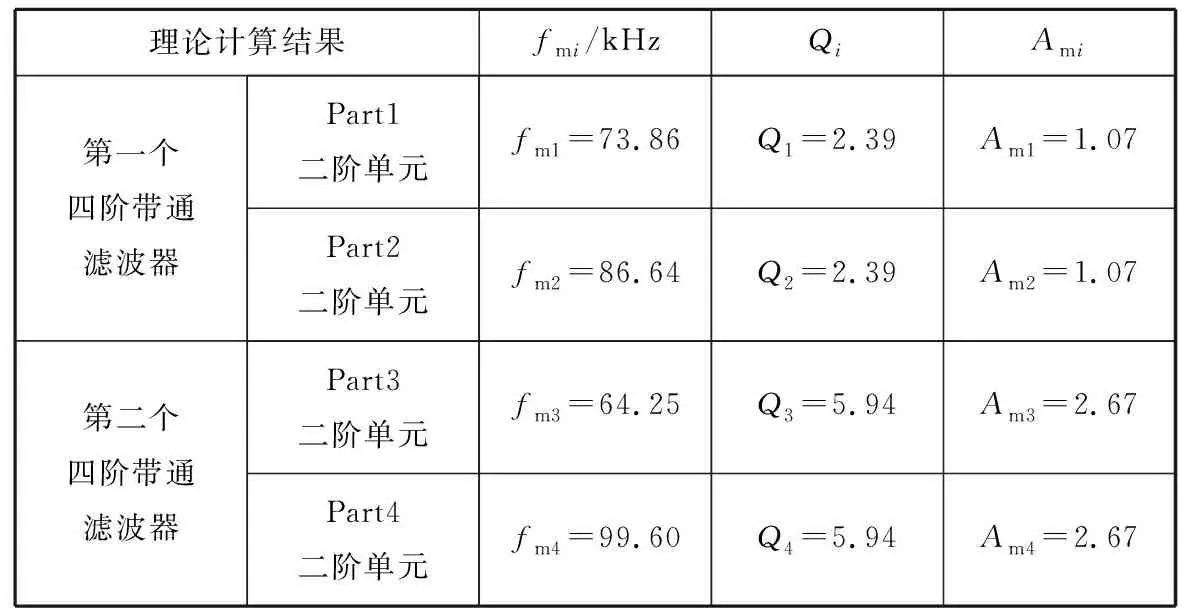
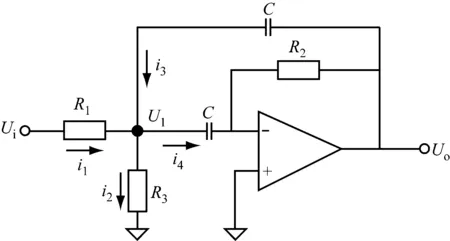
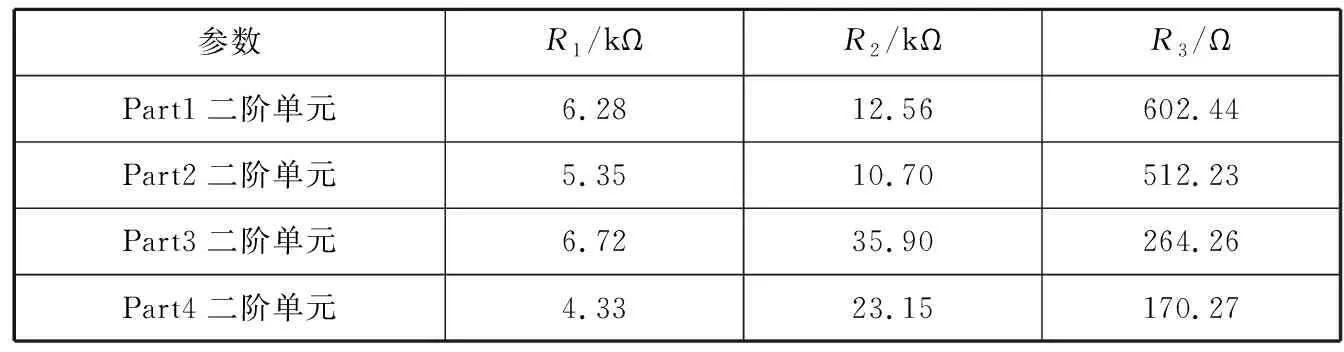
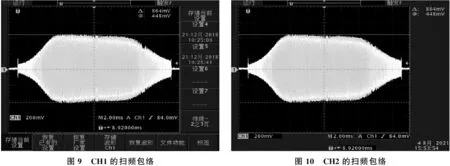
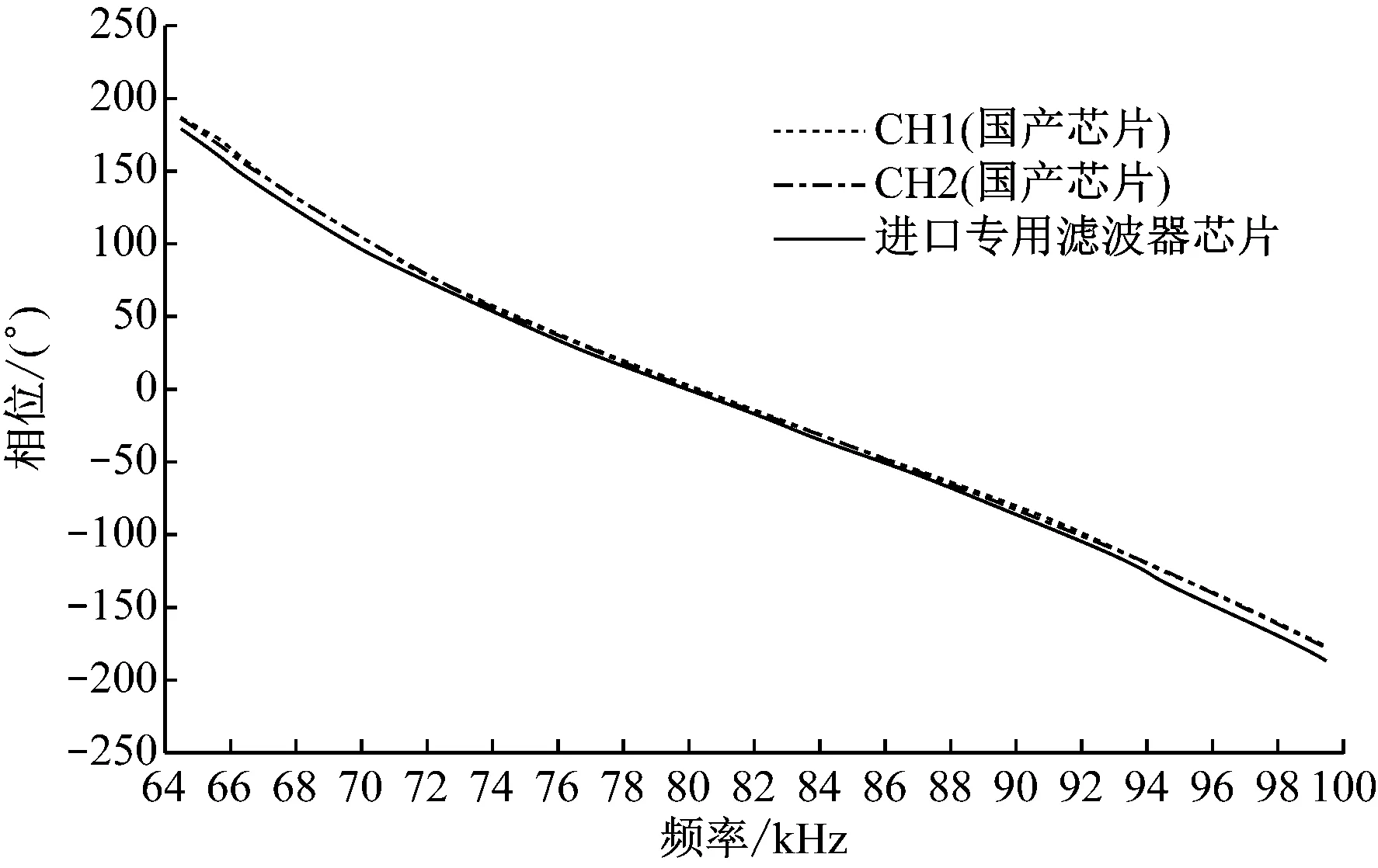
以此缩小取值范围。这里通过计算可得12 kHz 该参数的取值会使设计结果产生一定的误差,可根据仿真结果作进一步的调整,若误差较大,可在该范围内多次取值计算。这样可根据2个四阶带通指标确定每部分二阶带通单元的f0和Q指标。 图1 一个四阶巴特沃斯带通响应与其部分滤波器的幅频响应 2) 在一个四阶带通滤波器中,2个部分滤波器的中心频率被设计成与总滤波器的中心频率存在固定的系数比,这种方法称作参差调谐[1]。图1为一个四阶巴特沃斯带通响应与其部分滤波器的幅频响应。 四阶带通滤波器传递函数可写成2个二阶带通滤波器传递函数的乘积的形式,即 (7) 式(7)中:α为2个部分滤波器的中心频率与总滤波器的中心频率的固定系数比。α需采用逐次逼近法求取,计算公式[1]为 (8) 式(8)中:a1和b1为对应的二阶滤波器传递函数系数,需通过查表获得。 α的值确定之后,部分二阶单元的中心频率fmi和品质因数Q可通过以下公式确定。 由式(7)可知,二阶单元中心频率与总中心频率存在以下关系 (9) fm2=α·f0 (10) 式(9)和式(10)中:f0为滤波器总的中心频率;fm1为二阶单元1的中心频率;fm2为二阶单元2的中心频率。 2个二阶单元的Qi相等,即 (11) 式(11)中:Q为总滤波器的品质因数。 2个二阶单元中心频率处的增益Ami相等,即 (12) 式(12)中:Am为总滤波器中心频率处的增益。 3) 根据上述公式和预定义的2个四阶指标计算4个二阶单元的中心频率、品质因数和增益参数。 (1) 查询滤波器传递函数的系数表(见表2)[1]确定a1和b1的值。 表2 滤波器传递函数的系数表 由前述传递函数公式可知,八阶带通滤波器是由四阶低通滤波器转换而来的,而滤波器传递函数的系数表是以低通滤波器传递函数为基础得到的,因此a1和b1需按四阶带通滤波器传递函数取值。表3为选定的四阶带通滤波器传递函数系数值。 表3 选定的四阶带通滤波器传递函数系数值 (2) 根据式(8)确定α的值,其中ΔΩ的值结合表1中的预定义BW确定: ①第一个四阶带通滤波器归一化带宽ΔΩ1=0.187 5; 鉴于采用式(8)确定α的值过于复杂,利用MATLAB软件进行辅助计算,具体如下。 分别将第一个四阶带通滤波器和第二个四阶带通滤波器的a1、b1和ΔΩ代入以下程序中: ≫x=[1:0.001:2];%为减少程序运算时间,限定α(程序中为x变量)的取值范围以及递增系数 forj=1:length(x) A(j)=abs(x(j)^2+((x(j)*0.187 5*1.847 8)/((1+x(j))^2))^2+(1/(x(j)^2))-2-(0.187 5^2)); end M_A=min(A)%找到最接近0的函数值 将最接近0的函数值输入如下公式中: ≫symsx 思考:学生完成此问题时,要熟练掌握动点问题,相似三角形问题,直角三角形存在性等问题。如果教师在出这个题目之前有分解的小练,复杂问题定会迎刃而解。 f=sym('abs(x^2+((x*0.187 5*1.847 8)/((1+x)^2))^2+(1/(x^2))-2-(0.187 5^2))==2.325 0e-05');%输入最接近0的函数值,解出对应α m_x=solve(f,x) 通过上述程序算出的α值非唯一解,且有的解是复数,这里只取实数解。 ①第一个四阶带通滤波器的α值约为1.083; ②第二个四阶带通滤波器的α值约为1.245。 (3) 结合式(9)~式(12)计算各二阶单元的fmi、Qi和Ami的值,结果见表4。 表4 各二阶单元的主要技术指标的计算结果 能实现带通滤波器的电路技术有很多种,对比几种电路的优缺点,考虑到使接收机小型化,选择运算放大器数量相对较少、各项参数独立可调的多路负反馈型电路[3],电路形式见图2。 结合图2分析二阶单元的带通滤波器传递函数。对于U1,可将运算放大器看成微分器,则有 (13) 根据基尔霍夫电流定理,有 图2 一个二阶单元的多路负反馈带通滤波器电路 (14) 根据虚短、虚断,用电压表示上述电流,有 (15) 联立式(13)和式(15)可得到传递函数 (16) 将角频率代入式(16)中,有 (17) 比较式(4)和式(17)中的S项系数,可得 (18) (19) (20) (21) 根据式(19)~式(21)可得R1、R2和R3的表达式分别为 (22) (23) (24) 在计算外围电阻和电容的参数时,要先确定电容C的值,一般根据电容的量级与中心频率的关系表(见表5)[4]确定C的值。 表5 电容的量级与中心频率的关系表 根据设计指标中心频率80 kHz,这里选用C=820 pF。滤波器对电容精度的要求很高,精度越高,滤波器的一致性越好,因此这里取精度为1%。 结合式(22)~式(24)及表4中的fmi、Qi和Ami的值计算每个二阶带通单元外围器件的理论参数,结果见表6。 表6 各二阶带通单元外围器件的理论参数计算结果 根据水声接收机的应用要求和滤波器的技术指标,对于运算放大器的选择,首先要求运算放大器为高精度、低噪声的电压反馈型运等放大器,其次根据滤波器的频率f0和品质因数Q选择增益带宽积(GBW)合适的运算放大器。 增益带宽积按经验公式求取,即 GBW=f0·Q·100 (25) 由式(25)可得GBW=17.76 MHz,即本文设计的滤波器要求运算放大器的GBW≥17.76 MHz。 根据上述要求选择一款国产运算放大器,其芯片的主要技术指标见表7。 表7 选择的国产运算放大器芯片的主要技术指标 根据表6中的电阻参数进行仿真试验,根据计算的电阻值选用标称值最近的百分之一精度的电阻。根据理论计算结果微调部分电阻参数之后,得到仿真结果见图3~图7。 图7 级联后总的幅频响应和相频响应 根据仿真结果,最终调整的设计值符合指标要求,具体见表8和表9。 比较仿真结果与设计结果发现,二者在增益分配上存在比较大的差异,原因如下: 1) 为保证最终幅频响应的增益为0 dB,对各二阶单元的增益进行了微调; 2) 运算放大器芯片的开环增益曲线特性会对理论增益分配产生一定的影响,通过理论计算所得增益忽略了芯片本身的开环增益曲线特性。 表8 滤波器主要参数的仿真结果 表9 外围电阻标称值 为进一步评估设计方案的可行性,制作八阶带通滤波器的测试板。鉴于水声接收机对各通道的一致性要求,同时做多个通道,用以评估该电路的一致性。图8为单路八阶滤波电路原理图,其中2路滤波器的实测参数见表10。扫频包络图(扫频范围为55~110 kHz)见图9和图10,其中2路滤波器的带内相位曲线见图11。 图8 单路八阶滤波电路原理图 比较表10与设计指标可知,采用国产芯片搭建的八阶带通滤波器基本上能达到设计要求;由图9~图11可知,不同通道的幅频特性均满足巴特沃斯滤波器的特性要求,且频带内增益和相位特性的一致性良好。综上,本文采用国产芯片设计的水声信号滤波器的各项指标均能基本上达到设计要求。 表10 滤波器主要参数 图11 滤波器相位特性曲线 本文通过推导带通滤波器传递函数,引出了一种高阶带通滤波器二阶单元的理论计算方法,从而确定了滤波器各二阶单元的指标。在此基础上,选择适用的电路形式,基于合适的国产芯片进行仿真和实际电路测试,完成了水声信号八阶带通滤波器设计。实际测试结果表明,本文采用国产芯片设计水声信号滤波器的方案是可行的,相比直接采用进口专用芯片设计,虽然电路集成度稍低,设计过程相对复杂,但能有效实现自主可控。相信随着国内芯片行业的不断发展,未来一定会有国产的水声信号专用滤波器芯片出现。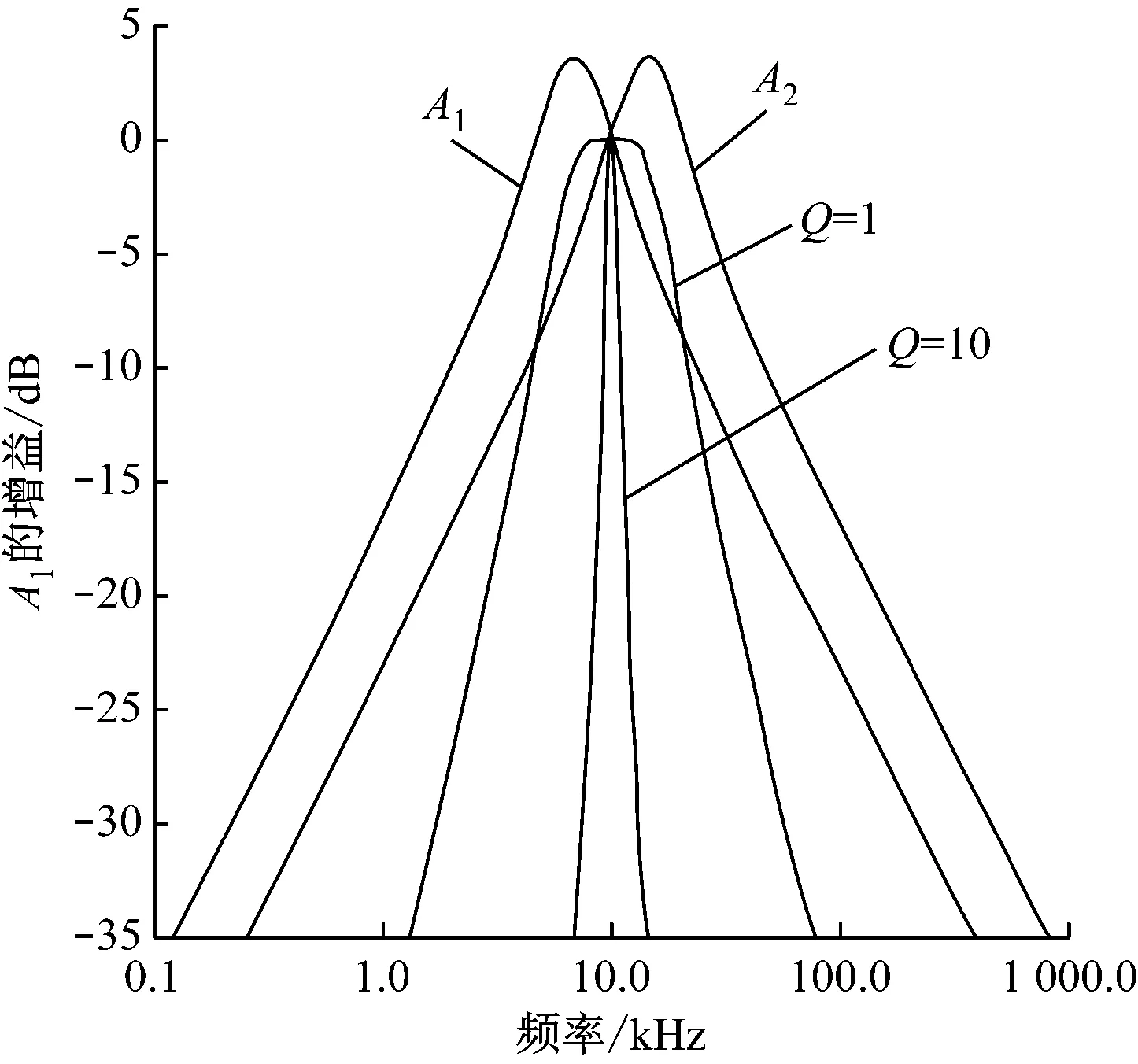
3 滤波电路形式的确定
4 外围器件理论值计算
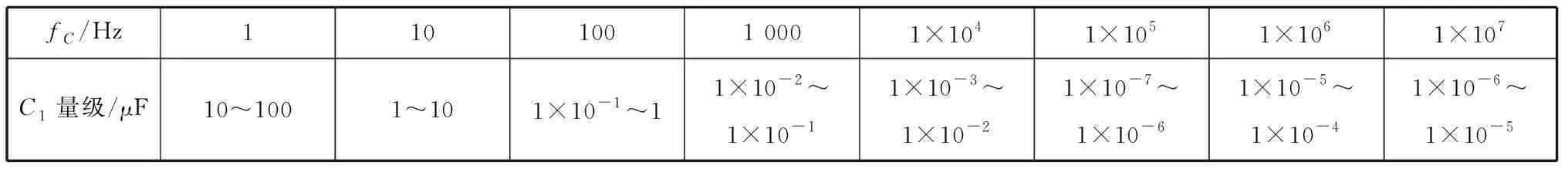
5 运算放大器选型和电路仿真
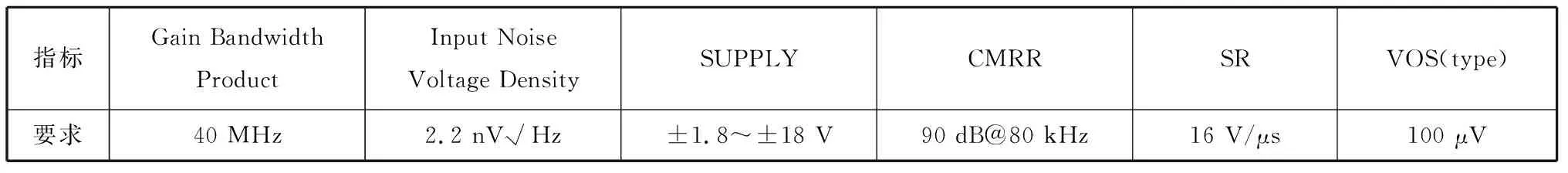
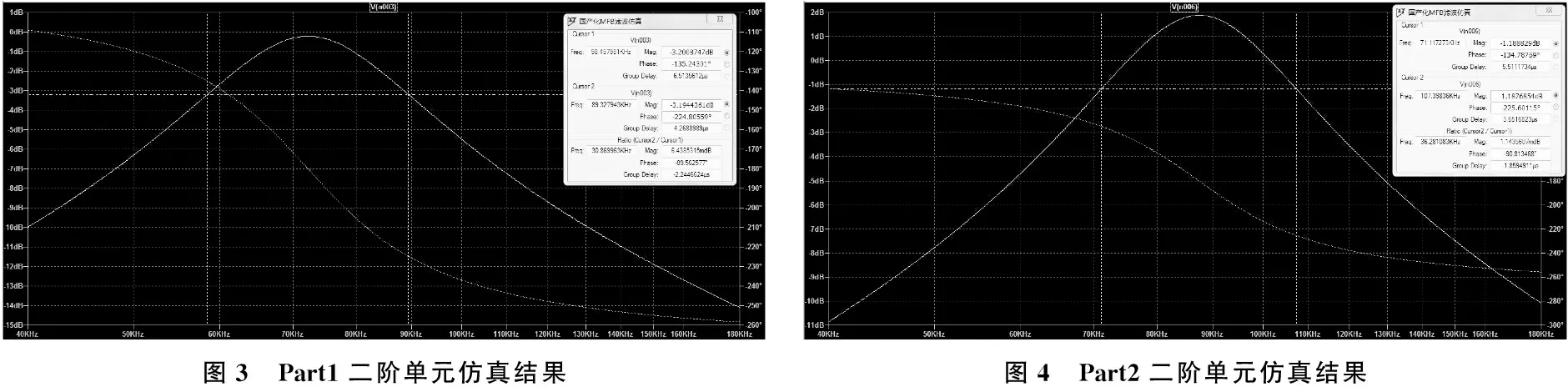
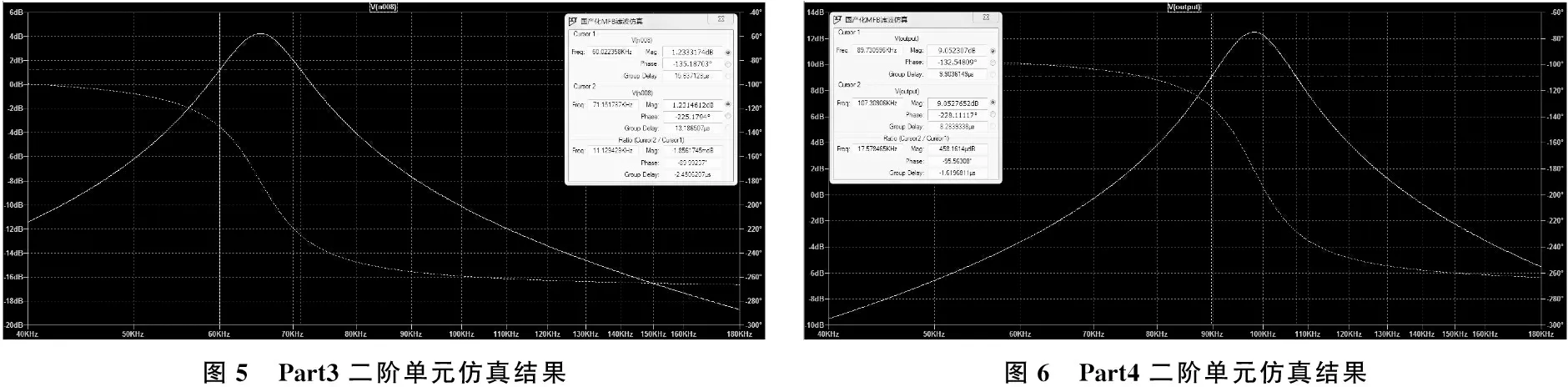
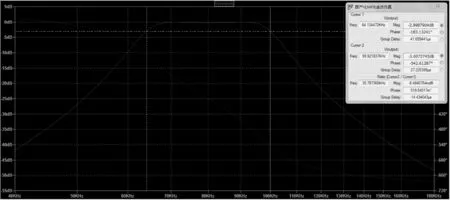


6 电路测试结果


7 结 语

