沥青路面结构验收弯沉值计算

吴晓荣 尚俊伟 彭光华

（中水淮河规划设计研究有限公司 合肥 230601）

1 引言

道路建设工程质量不仅关系到行车安全，而且直接影响自身的耐久性、舒适性。道路的损坏虽然有雨水、温度、车辆荷载等外部因素，但最主要因素还是自身施工质量。因此提高道路施工质量，才是提高道路使用耐久性的关键所在。在早期沥青结构道路中，由于荷载和交通量相对较小，路面薄且结构单一，弯沉值能够较好地反映路面的承载能力，控制竖向变形，因此长期以来弯沉值不仅作为验收指标而且作为设计指标在控制施工质量方面发挥着重要的作用。但是随着路面结构越来越多样，影响路面性能的因素也越来越多，以前的设计方法与现行工程要求越来越不适应，因此在最新颁布的《公路沥青路面设计规范》（JTGD50-2017）中，对沥青路面的设计指标进行了较大调整，采用多指标的方法对路面结构进行设计，仅把弯沉值作为验收指标列入规范对工程质量进行控制，要求路面交工时的实测弯沉值应小于验收弯沉值，并对弯沉值的计算方法和检测方法进行了修改，本文结合南四湖二级坝坝顶道路实例，对沥青路面结构弯沉值中的路表弯沉值的计算方法和检测方法进行示范应用。

2 工程概况

南四湖二级坝水利枢纽工程横跨昭阳湖湖腰最窄处，工程东起老运河西堤（湖东堤），西至顺堤河东堤，全长7360m。二级坝枢纽属大（1）型工程，其主要建筑物拦湖土坝为1 级建筑物，坝顶公路为二级公路标准，设计使用年限为12年。根据交通量OD调查分析断面大型客车和货车交通量为2421 辆/日，交通量年增长率7%，方向系数取55%，车道系数取100%。由交通历史数据，确定该设计公路为TTC4 类。计算本公路设计使用年限内设计车道累计大型客车和货车交通量为8690477，交通等级属于重等交通。路基主要为二级坝堤身土，经过长期车辆碾压，承载力较高，局部软弱路基采用水泥土换填处理。路面结构通过比选采用沥青混凝土结构，路面结构设计根据汽车荷载、工程地质和材料物理力学指标等综合因素，计算确定路面结构的强度组合和厚度。该工程沥青路面结构结合以往工程成功经验拟定结构形式：从上至下各结构层为：40mm 细粒式沥青混凝土AC-13（C）、60mm 中粒式沥青混凝土AC-20（C）、透层、水泥稳定碎石20cm、低剂量水泥稳定碎石25cm。标准段坝顶道路总宽度12m，其中行车道宽度9m。

3 理论原理和假设

根据道路路面结构体系的特点，路面层状结构坐落在路基上，路基坐落在半无限深的地基上。由于不同材料层组成的路面结构的抗疲劳性和使用的耐久性，不允许各结构层在行车作用下产生塑性变形的累加，尽量将变形控制在弹性工作阶段，加之高等级道路较厚的结构厚度、较高的强度、行车作用的瞬时性（通过路面某点的时间很短），故长期以来设计过程中一般将其视作线性弹性体，应用弹性层状体系理论对其竖向位移进行计算分析。

弹性层状理论的基本假设为：（1）每一层均由均质各向性的以及位移和形变是微小的线性弹性材料组成，其弹性参数以回弹模量和泊松比组成；（2）最下层在水平方向和垂直向下方向为无限大（弹性半空间体），其上各层在水平方向无限延伸但竖向具有一定厚度；（3）各层分界面上的应力和位移完全连续或者竖向的应力和位移连续而层间的摩阻力为零；（4）各层在水平方向无限远处及最下一层无限深处的应力、应变和位移均为零；（5）不考虑自重；（6）将标准轴载一侧的双轮荷载简化成两个半径为δ的圆形均布荷载。

该弹性体系下的路面结构计算模型见图1。

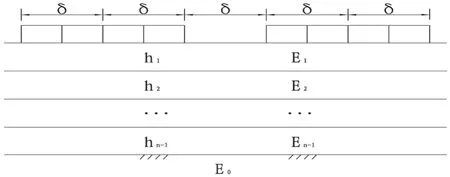
图1 路面结构计算模型图

随着数学和弹性力学的进步，国内外众多学者都对该模型的位移和应力求得了理论解，推动了这一理论和模型在工程中的快速应用和发展。

4 路表验收弯沉值计算

4.1 计算方法

根据《公路沥青路面设计规范》（JTGD50-2017）的规定，验收弯沉值la采用层状弹性体系理论按照以下公式进行计算：

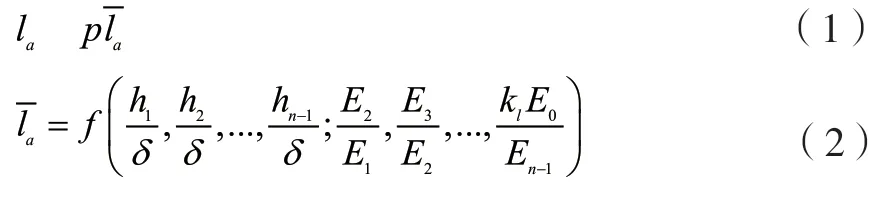
式中：为理论弯沉系数；p和δ分别为标准轴载的轮胎接地压强和当量圆半径；kl为土基模量调整系数。

4.2 计算参数的确定

4.2.1 各层材料参数

根据规范规定，式（2）中无机结合料层材料参数应采用20℃下的动态力学参数。该工程中沥青路面各层材料参数详见表1。

表1 沥青路面结构各层材料参数表

4.2.2 土基调整系数

根据规范规定，无机结合料稳定类基层沥青路面取0.5，粒料类基层沥青路面和沥青结合料基层沥青路面，当采用无机结合料稳定底基层时，取0.5，否则取1.0。该工程基层采用水泥稳定碎石，底基层采用低剂量水泥稳定碎石，均属于无机结合料，故土基调整系数kl取值0.5。

4.2.3 轮胎接地压强和当量圆半径

根据规范规定，轮胎接地压强p和当量圆半径δ应为标准轴载下的值，故取p=0.7MPa，δ=213.0mm。

4.2.4 理论弯沉系数

理论弯沉系数作为验收路表弯沉值计算中最复杂也是最重要的参数，可通过先求单圆荷载下多层弹性体内任一点的位置，然后通过坐标系转换、位移叠加计算等转换，求得双圆荷载下的位移和，进而求得路表弯沉值。这种理论计算的弯沉系数解析式如下：

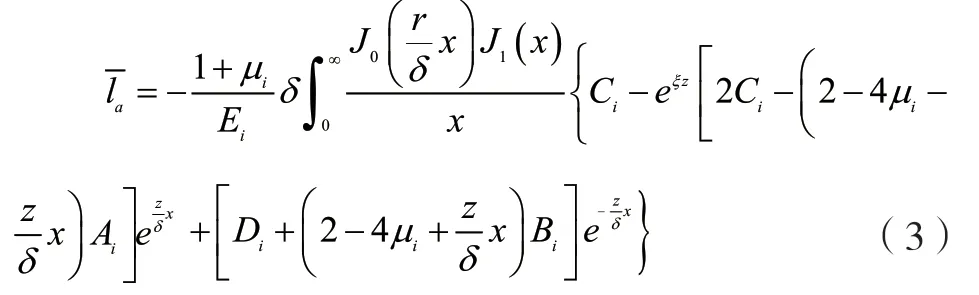
式中：i为下标量，表示所在层数；J为贝塞尔函数；Ai,Bi,Ci,Di为积分常数，根据具体力学问题的定解条件确定。根据上述理论计算公式，借助成熟的商业软件如BISAR 等可求得其路表弯沉值。

在无商业软件的情况下，也可基于弯沉等效原则将实际的多层体系转换成标准三层体系，如图2。

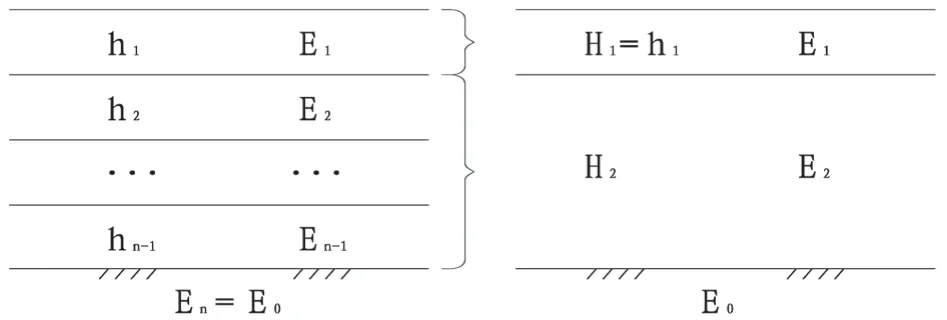
图2 路表弯沉计算三层结构转换图

采用近似计算公式计算。这样在没有专业路面设计软件的情况下，也可以通过手算或者借助电脑编程方法进行计算，具体方法如下：

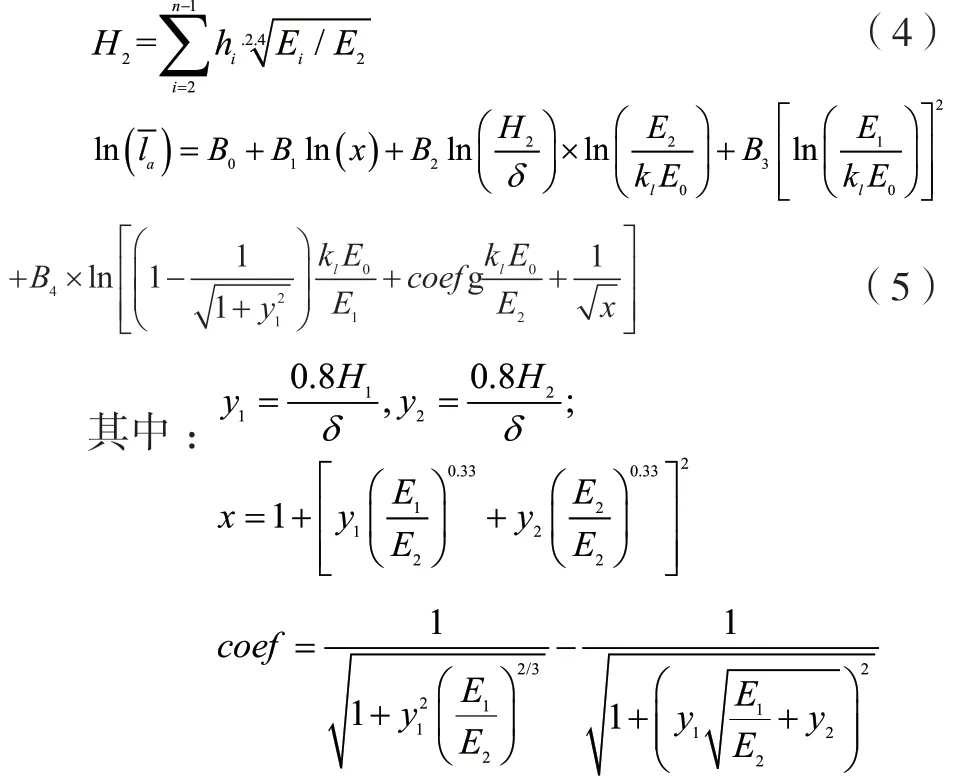
4.3 计算结果

本工程在进行路表弯沉值计算时选择采用商业软件进行，将路面结构的各项基本参数代入程序，计算出二级坝坝顶道路的验收路表弯沉值为21.4（0.01mm）。

5 检测要求

根据规范要求，路表弯沉值的检测宜采用落锤式弯沉仪进行现场检测。落锤式弯沉仪的荷载为50kN，荷载盘半径应为150mm，一般选择1～3km 为一个检测路段。另外实测路段的弯沉值还应考虑湿度以及温度的影响，对实测值进行修正，修正后的实测值小于设计提供的路表验收弯沉值方为合格。

6 结语

本文基于2017 版《公路沥青路面设计规范》，结合二级坝除险加固工程坝顶道路工程实例，从理论原理、结构模型至具体计算方法，详细叙述了沥青路面结构路表弯沉值的计算过程，为设计人员对类似沥青路面结构计算提供一定的参考■