模块化矢量轮底盘的设计与控制

武书昆 汪睿翔 奚雨涵 石 睿 冷春涛

Wu Shukun Wang Ruixiang Xi Yuhan Shi Rui Leng Chuntao

0 引言

在一些工况条件下，如仓储、搬运等环节，由于空间狭小，对运动底盘的灵活性要求较高。随着近些年来的发展，出现了诸如麦克纳姆轮底盘、90度全向轮底盘、两轮差速底盘等驱动形式，上述底盘类型运动灵活性高，但抓地力与驱动力相对较差。

矢量轮底盘，又称“Swerve Chassis”，是近二十年内逐步发展的一种底盘驱动形式。矢量轮底盘由若干个矢量轮模块(Swerve Module)组成，每个模块由转向和行驶两套动力系统组成，各模块可以独立地360度任意角度旋转，独立地配置行驶速度[1]。通过控制各个矢量轮模块的角度和行驶速度，矢量轮移动底盘可以实现任意方向、任意轨迹的运动，同时具有极强的机动性、高抓地力[2]。

本研究设计开发了一款模块化的矢量轮底盘，其中的矢量轮模块由两个独立的上置式电机提供动力，通过直齿轮、行星齿轮、锥齿轮等一系列的减速传动，驱动行驶与转向两套系统，实现各个模块独立的行驶和转向。通过有限元仿真验证了核心零部件的强度，并提出模块化矢量轮底盘的控制逻辑。

1 矢量轮模块的设计

对于矢量轮底盘来说，是由若干个按照一定规律排列的矢量轮模块组成，底盘的运动时各个模块单元运动的矢量叠加。常规的矢量轮底盘一般有三个或四个模块组成，模块之间相互独立，每一个模块具有独立的行驶系统和转向系统[3]。本设计目标是具有四个模块的矢量轮移动底盘在负载100 kg的情况下，高机动性、高附着力地实现5 m/s全向运行。

图1 矢量轮底盘

图2 矢量轮模块

1.1 行驶系统设计

根据每个模块25 kg负载，5 m/s的工作状态，并且为了获得比较好的加速性能，推算出行驶系统的电机输出功率在200 W至400 W之间，且要有较高的输出效率。行驶电机的转速低一些，便于做减速传动。

根据上述需求，本研究选取Falcon 500电机作为行驶动力电机。该电机为无刷电机，驱控一体化设计，并内置编码器与温度反馈，支持CAN通信、PWM控制。Falcon 500电机在12 V供电下，空转速度为6 380 r/min，在300 W输出功率时的效率约为86%，最大功率783 W，堵转电流257 A。图3为Falcon 500电机输出性能曲线。

图3 Falcon 500电机性能曲线

为了取得一定的越障能力，选取驱动轮的直径为5英寸(127 mm)。驱动轮毂与大伞齿轮一体化设计，齿轮参数为1.25模，75齿，与其配合的小伞齿轮为1.25模15齿，实现末端传动。电机输出端为1.5模16齿，配合1.5模24齿齿轮，实现起步传动。综合减速比为7.5。

图4 行驶部分减速设计

1.2 转向系统设计

为了模块灵活转向，需要转向系统在0.1s内完成最大90度的转向。根据轮胎与地面约0.3摩擦系数，以及负载状态，推算转向系统的输出功率在30 W至60 W。

根据上述需求，本研究选取775Pro电机作为转向动力电机。该电机为有刷电机，体积小，动力足。该电机在12 V供电下，空转速度为18 300 r/min，在50 W输出功率时的效率约为70%。图5为775Pro电机输出性能曲线。

图5 775Pro电机输出性能曲线

转向系统需要较大的扭矩实现轮毂方向的高速转向，其转速在300 r/min左右。选取末端为带传动，大带轮型号选取HTD-5M圆弧形齿，齿数由空间尺寸决定，取60齿，小带轮取10齿，带宽12 mm。大小带轮之间在计算中心距的基础上，增加0.2 mm的涨紧量，保持同步带的绷紧。整体减速比为56。图6为转向系统减速设计。

图6 转向系统减速设计

2 矢量轮模块核心零件的设计与仿真验证

本研究针对轮毂支架的进行优化设计与仿真。如果轮毂支架部分仅使用紧固件固定，造成整体结构抗弯性能不足，应力集中现象较为明显。经过仿真验证，矢量轮模块使用阶梯轴将两端支架顶住，并使用横向紧螺栓锁故，使之形成较为稳定的框型结构，能够较好减小相关零件所受应力。

采用轮毂支架部分的简化模型，使用SOLIDWORKS Simulation对该部分进行仿真。本次仿真模拟了未安装和安装了阶梯轴的受力情况，对横向螺栓、两侧支架、阶梯轴和相关轴承进行了强度校核。

仿真过程中，对整体模型进行了如下简化和参数设置。将两支架上表面设为固定，各零件的接触为全局接触；两支架间使用螺栓螺母固定，给定初始扭矩为2 N·m，摩擦系数为0.3。根据对实际情况的预估，施加对支架一侧的外部载荷，大小为200 N。以2 mm为网格划分大小，得出如下计算结果。

图7 没有安装顶轴时应变和应力分布

分析中最大应力点数值为24.49 MPa，最大应力点在支架孔端出现，即轮毂支架呈现“悬臂梁”状态。对等应变范围最高值为1.881e-04。

装配好阶梯轴后，使用相同参数对模型再次网格化，进行计算分析，得出如下结果。

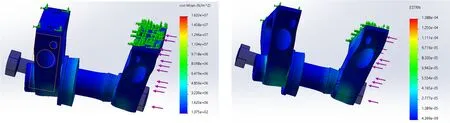
图8 安装顶轴时应变和应力分布

分析中最大应力点数值为15.09 MPa，最大应力点也在支架孔端出现。对应应变范围最高值为1.388e-04。

制作两侧支架的材料为6061 T6铝合金，抗拉压强度为260 MPa。在两种给定载荷的情况下，拉压应力均在强度校核的许用范围内。在装配顶轴后，最大应力数值有较大幅度减少，减少为原值大小的61.62%；对等应力范围的最高值减少为原值大小的73.79%。该设计较好地提高了轮毂支架的承载能力与强度。

3 模块化矢量轮底盘的控制

3.1 控制逻辑

对于多个模块组成的矢量轮底盘，底盘的几何中心是运动控制的基准。外部指令或内部运算结果给出底盘几何中心在某一时刻速度的横移速度、前进速度和自旋转速度，根据各个模块相对于几何中心位置进行向量分解，推导出各个模块的运动方向与速度，即逆运动学计算。最后，各个模块的行驶系统与转向系统独立地做运动学的闭环控制，实现各个模块按照解算结果运动，共同推动几何中心按照既定的方式运行。

3.2 长方形底盘的逆运动学解算

在实际的应用过程中，四个模块组成的长方形矢量轮底盘居多，接下来以此为例，介绍长方形底盘的逆运动学解算。底盘的几何中心任意时刻的运动可用三个参数描述：横移速度、前进速度、自旋转速度，按照以下步骤计算出每个模块的朝向，及车轮的速度。

第一步：确定机器参数

逆运动学方程首先需要确认底盘的长宽尺寸。在后续的计算中只使用长宽的比值，长宽可以使用任意单位。要注意的是，决定底盘运动的是模块的位置，因此程序中填入的长和宽应当是模块的轮子与地面接触点组成的长方形的长宽，而不是底盘轮廓的长宽。设长度为L，宽度为W，对角线长度的一半为R。有以下公式：

(1)

第二步：获取输入变量并计算

逆运动学计算输入：横移速度、前进速度、旋转速度，三个变量，三个量范围分别为-1到1。横移正方向为右，旋转正方向为顺时针。在计算过程中设置四个中间变量，用来简化计算，分别是：A、B、C、D，计算值如下：

A= 横移速度- 旋转速度·(L/R)

(2)

B= 横移速度+ 旋转速度·(L/R)

(3)

C= 前进速度- 旋转速度·(W/R)

(4)

D= 前进速度+ 旋转速度·(W/R)

(5)

对四个模块进行标号，模块1～4分别指：右前方模块、左前方模块、左后方模块、右后方模块(从右前方逐渐逆时针数)。则四个模块的计算结果为：

(6)

(7)

(8)

(9)

注：atan2(x，y)是多数编程语言中的常规函数，返回以弧度表示的y/x的反正切。y和x的值的符号决定了正确的象限，也可以理解为计算复数x+yi的辐角[4]。

4 结论

本文设计了一种由若干矢量轮模块组成的矢量轮底盘。每个矢量轮模块有独立的行驶和转向两套动力系统，这两套系统由行驶电机、转向电机经过直齿轮、行星齿轮、带齿轮、带传动等减速获得合适的速度与扭矩。通过对重要部件简化建模，使用SOLIDWORKS Simulation模块，优化设计了轮毂阶梯轴，仿真分析了轮毂支架同阶梯轴的传力特性及应力应变分布，得到了简化模型下1.62倍的强度提升。矢量底盘的运动控制是几何中心的运动得到目标后，解算到若干个模块，获得各个模块的行驶速度和方向，进而实现底盘的正确运动。