金华市某岩质滑坡成因机制分析及发展趋势预测

雷梦茹,徐光黎,张泰丽,薛孟奇,薛 媛,赵宏涛

(1.中国地质大学(武汉),湖北 武汉 430074;2.中国地质大学(武汉)地质调查研究院,湖北 武汉 430074;3.中国地质调查局南京地质调查中心,江苏 南京 210016)

滑坡等突发性地质灾害频发,严重危害东南沿海人民群众生命财产安全[1]。因此,提升滑坡成因机制研究、滑坡预测及预报技术,对解决滑坡防治等难题具有重大的现实意义。在滑坡灾害研究过程中,尚敏等[2]、常亚婷等[3]针对不同滑坡成因机制进行分析,研究表明不同滑坡受所处地质条件的差异影响,成因机制需针对具体滑坡开展针对性研究。同时,为了更有效预测滑坡发展趋势,建立模型来分析、评价和预测滑坡稳定性成为众多学者的研究方向。目前,已形成众多专业性的分析模型[4-5],如小波分析模型[6-8]、多因素回归分析模型[9]、灰色理论模型[10-13]、人工神经网络模型[14-16]等,其中灰色GM(1,1)模型以其“小样本、贫信息”的独特优势被广泛应用于许多预测领域并取得了很好的效果。容静等[17]提出了基于小波的GM(1,1)-AR模型,有效剔除了多余噪声,预测结果更为精确。传统的GM(1,1)模型在长期预测时,数据序列拟合较差,预测精度偏低。在实际工程应用中,随时将每一个新得到的数据置入系统中,建立新信息GM(1,1)模型,进行灰色动态新陈代谢GM(1,1)滑坡预测(简称MGM(1,1)模型),可以有效降低预测误差。结合实际监测数据,运用灰色-马尔科夫模型修正滑坡变形预测值,可以有效提高预测精度,灰色-马尔科夫动态新陈代谢GM(1,1)模型(简称MGM(1,1)-MC模型)精度较高,预测误差较小,有很好的工程应用价值。

1 滑坡工程地质概况

该岩质滑坡隶属金华市婺城区雅畈镇(图1)。原有自然地形坡度20°～40°,因工程施工等原因发生了极大的改变,山体南侧开挖形成高陡边坡,边坡最大高度约60 m,总体坡度达69°,滑坡体内冲沟发育,从西到东依次发育4条冲沟,深5～14 m,宽8～20 m,存在间隙性流水。

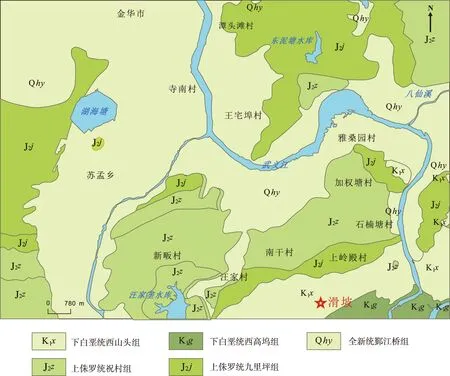
图1 金华市某岩质滑坡区域地质图Fig. 1 Regional geology of a rock landslide in Jinhua City

滑坡体平面形态总体呈马蹄形,主滑方向总体向北,滑体厚度为15～30 m,轴线水平长约190 m,前缘宽约290 m,后缘宽约240 m,面积约5.5万 m2(图2)。滑体物质主要为第四系(Q4)残坡积土,厚度15～35 m,下白垩统西山头组(K1x)流纹质晶玻屑凝灰岩,自身结构面较发育,结构杂乱,无统一性。滑带位于下白垩统西山头组(K1x)凝灰质长石砂岩夹粉砂岩层内,该层与上下岩层的界面之间的结构面,是潜在的较深层滑面。下伏地层主要为下白垩统高坞组(K1g)微风化流纹质晶屑凝灰岩,地层裂隙较少,较完整,滑坡工程地质剖面见图3。

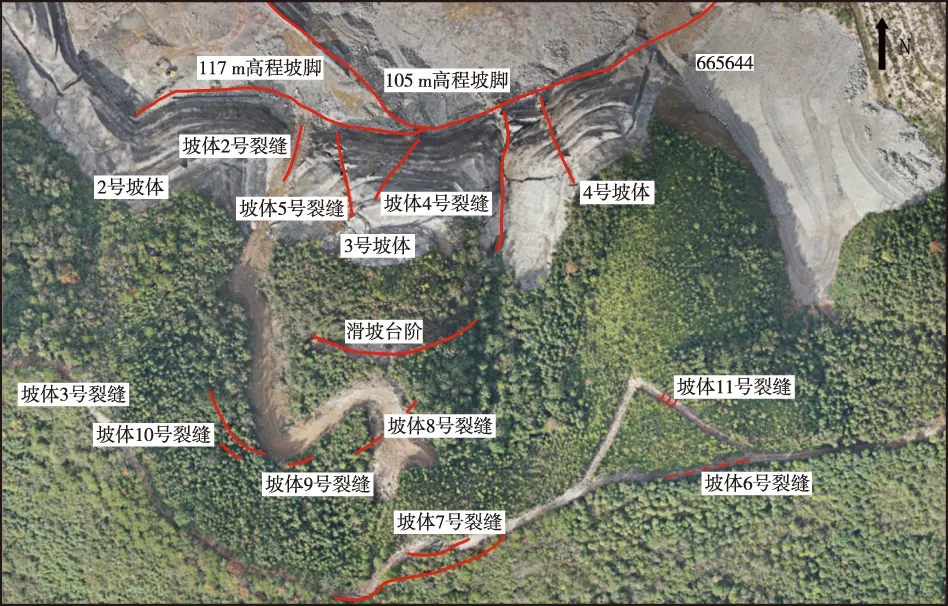
图2 金华市某岩质滑坡全貌图Fig. 2 A full view of a rock landslide in Jinhua City

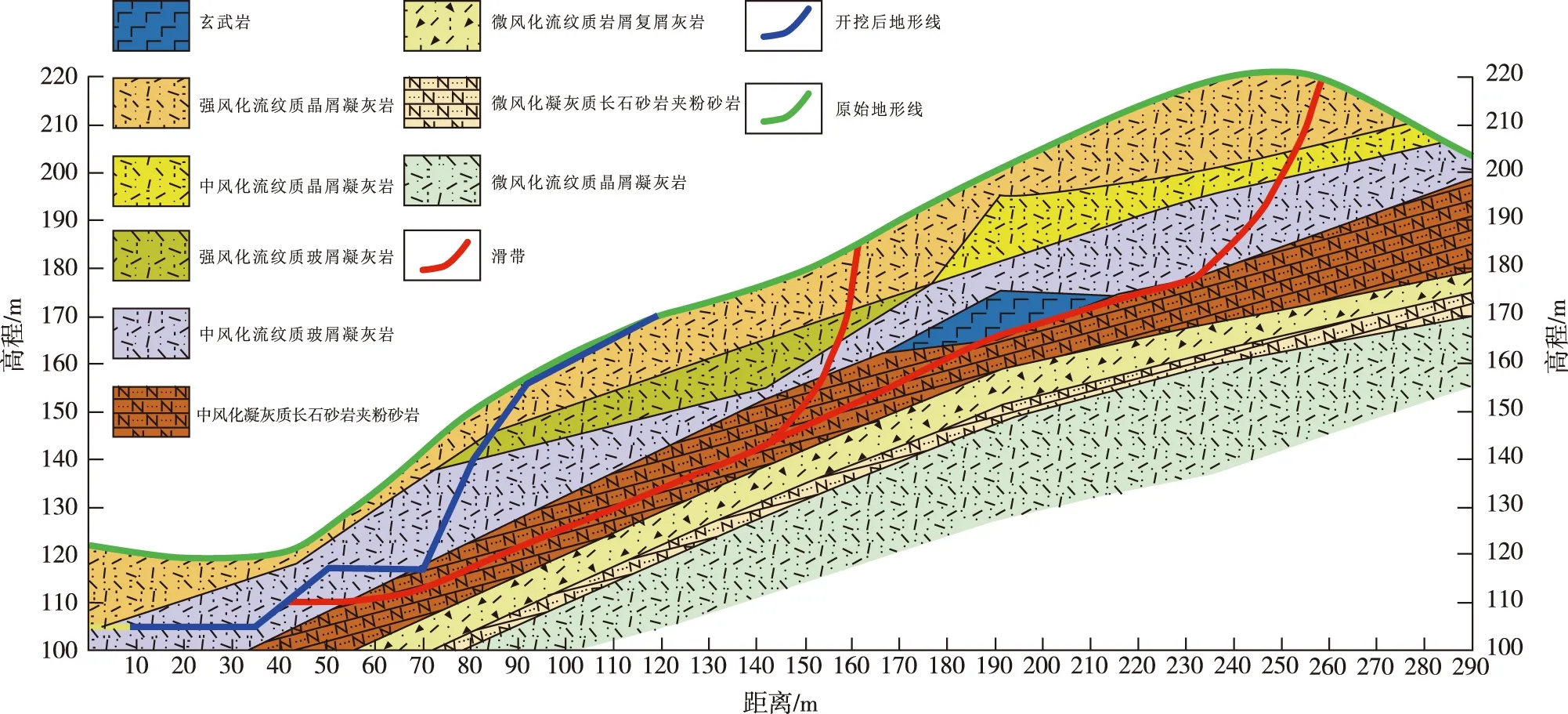
图3 金华市某岩质滑坡剖面图Fig. 3 Cross-section of a rock landslide in Jinhua City

区内水文条件较发育,具体特征如下:①地表水特征。滑坡体范围各个坡体的沟谷之间分布有自然冲沟,雨季形成水流。地表径流条件好,受其影响,一般短暂的大雨,雨水多沿地表汇聚到冲沟里快速流走,入渗于地下的水量较小;短暂的小雨,雨水多在地表蒸发,入渗到地下的水量亦较小。②地下水特征。坡体浅表含水层主要赋存于第四系残坡积层,结构松散,透水性较好。补给源以大气降水为主,垂直下渗补给基岩裂隙水。地下水水位、水量动态变化较大,受气候影响明显。

总体来说,该滑坡区地形条件、水文条件及物源条件均较充足,易于形成滑坡。对其成因机制及发展趋势研究具有重要意义。

2 滑坡形成机制及其破坏因素分析

该滑坡经历了自然斜坡-人工边坡-滑坡复杂的演化过程。按照对斜坡、滑坡产生影响的作用形式,可分为内在因素和外在因素两个方面。内在因素包括地形地貌、岩土体性质、地质构造、坡体结构特征、地应力等,它们通常起着主要的控制作用。外在因素有人工切坡、地下水、大气降雨、震动等,它们多是斜坡演化成滑坡的诱发、触发因素。该滑坡的形成是受内在因素(地形地貌、地层岩性和地质构造等)与外在因素(地下水作用、大气降雨及人类活动等)综合作用的结果。

2.1 内在因素

(1)地形地貌。滑坡地貌类型属丘陵地貌,自然地形坡度一般为20°～40°,坡面形态多呈凸形,在纵向上呈线性陡坡和相对缓坡的坡形组合模式。

(2)地层岩性组合。滑坡表面由第四系松散残坡积物和全风化层组成,其下为浅紫色流纹质晶屑凝灰岩、浅灰色英安质晶玻屑熔结凝灰岩等碎裂岩,裂隙面上见3～5 cm厚的绿泥石化夹层(图3)。残坡积物主要以碎石土、粉质黏土夹碎石为主,夹碎块石,呈黄褐色,表面风化程度强烈,具有较强透水性,遇降水很难形成地表径流,多直接下渗。下伏凝灰岩属于火山多次喷发堆积形成,喷发间歇期沉积了薄层泥岩、粉砂岩,或形成不同程度的风化壳,且地层裂隙极为发育,呈碎裂岩,为降水提供良好的下渗通道,直达坡体内部,在挤压破碎带与微风化基岩面交界处遇阻汇聚,软化、破坏交界面的强风化凝灰岩。凝灰岩滑带土物质成分主要由长英矿物、绢云母、黏土矿物等亲水矿物组成。在地下水的长期作用下,滑带土强度会大幅度降低,加大滑坡失稳的可能性。

(3)地质构造。滑坡地质构造是受燕山期构造活动和喜山期构造活动的影响,形成了一系列的构造节理与负地貌。滑坡左、右边界明显受近SN向大型节理(断层)控制;后缘北山体被内部广泛发育的陡倾节理所切割而分离。坡体结构为顺层结构,产状8°～330°∠17°～38°,流面(层面)密集,软弱夹层或挤压顺层发育,平直,贯通性好。滑坡的边界、切割面、滑动面与地层破碎程度均与区域地质构造密不可分,是构成滑坡最重要的内在因素。

滑坡在坡体浅部发现有一处结构面连续贯通。结构面的连续贯通为滑坡的发生发展提供了最为关键的条件,是滑坡发生的核心内因。

2.2 外在因素

(1)人工切坡。该滑坡形成之前为自然斜坡,在长期自然地质演化过程中处于自然平衡状态。在历次的地质灾害调查中,并没有发现此处存在该滑坡。后期为了工程修建需要,形成了高达近60 m的超高陡边坡,总体坡度达69°。人工切坡在极短时间内改变了原有坡体的应力平衡。一方面,开挖坡脚使得原有埋藏在地下的构造结构面暴露出地表,为坡体剪出提供临空条件;另一方面,开挖坡脚,卸荷减重,极大地改变了原地应力场,为地层回弹提供了可能,会因此形成一个最大剪应力增高带,通常是边坡中最容易发生变形破坏部位。在坡肩部位,在一定条件下,形成一个张力带,地层容易被拉裂形成与坡面近于平行的拉裂面。

(2)地下水作用。地下水是影响边坡稳定最重要的外在因素,其对边坡稳定的影响重大。2号、3号和4号边坡两侧均有冲沟发育(图2),是地表水汇集、入渗之处。由于滑动面在在冲沟处埋深浅或者直接出露,地下水可以直接渗入到滑动面。地下水顺坡向径流,在第四系松散堆积物与基岩风化带接触部位、强弱风化界面以及与构造破碎带的接触部位,因岩土渗透性的差异形成地下水作用的活跃带,并发展成为斜坡破坏的潜在滑动面。地表水通过裂缝渗入滑坡岩土体中,多沿完整性较好的基岩顶面一带渗流,水饱和后对滑面起到润滑作用,软化滑带岩土体,形成软弱结构面(带),为滑坡的滑动提供了有利的滑动介质。

3 MGM(1,1)-MC模型构建

MGM(1,1)-MC模型是将灰色系统理论和马尔科夫理论相结合建立的预测模型,既解决了灰色模型对波动较大的数据样本预测精度不高的缺陷,又弥补了马尔科夫模型要求数据具备平稳过程的局限性[18]。传统GM(1,1)模型考虑的是在某一时刻t=t0时前期的所有数据建模,但随着时间的推移,监测工作越往后开展,系统将会受到更多新的扰动因素,这将对传统的模型产生较大影响[19-20]。为了反映目前的系统特征,必须逐步降低老数据的信息意义,不断补充新数据的信息意义,经历一个“新陈代谢”的过程,提高模型的预测精度。在此基础上通过马尔科夫模型对预测结果进行修正,提高预测精度,建立起MGM(1,1)-MC模型[21]。本滑坡监测数据波动性较大,使用MGM(1,1)-MC模型可以有效减少数据波动,提高预测精度。

3.1 MGM(1,1)模型构建

记x=(x(1),x(2),…x(n))其中x(i)表示为原始监测点累计位移量观测数值[22]。

步骤1:令x(0)为GM(1,1)建模序列,表示灰导数,

x(0)=(x(0)(1),x(0)(2),…,x(0)(n)),

(1)

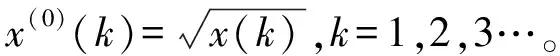
(2)

步骤2:令x(1)为x(0)的AGO序列,对x(0)作累加生成,即得到新的序列,

x(1)=(x(1)(1),x(1)(2),…,x(1)(n)),

(3)

x(1)(1)=x(0),

(4)

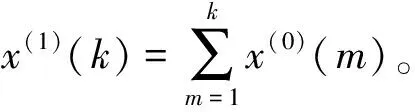
(5)

步骤3:令z(1)为x(1)的均值序列,表示白化背景值,

z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1),

(6)

z(1)=(z(1)(2),z(1)(3),…,z(1)(n)),

(7)

得到GM(1,1)的灰微分方程模型为

x(0)(k)+az(1)(k)=b,

(8)

式中:a,b为待估计参数,分别称为发展灰度和内生控制灰度。其中,

a=

b=

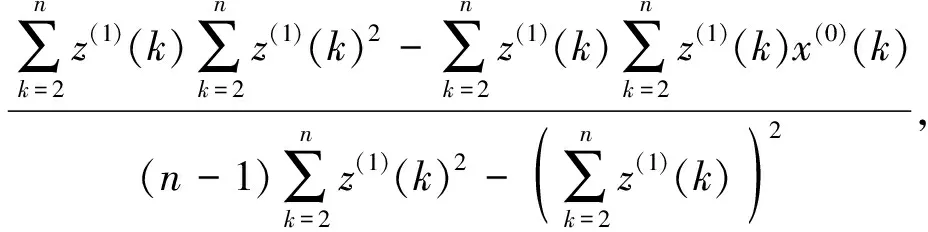
(9)

经变换后得到

x(0)(k)=b-az(1)(k)。

(10)

步骤4:GM(1,1)模型的求解:在(9)两端同时乘以eak得到

eakx(0)(k)=eakb-az(1)(k)eak,

(11)

可以推算得出时间函数x(1)(k+1)的估计值

(12)

以上即为GM(1,1)模型的建模过程,其中-a称为发展系数,b为灰色作用量。

步骤5:数据剔除与代谢。将原始序列第一个数据x0(1)剔除[23],引入新数x0(n+1),该数据序列与原始数据序列等维,在剔除最原始数据的基础上又加入了等量的新数据,对系统进行了新陈代谢,形成新的时间数据序列

x(0)=(x(0)(2),x(0)(3),…,x(0)(n+1))。

(13)

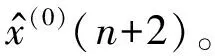
重复以上步骤,直到达到预期的预测目标为止,上述过程称为MGM(1,1)模型的预测过程。

3.2 灰色-马尔科夫模型构建

马尔科夫模型可以依据目前事件状态对未来时间段状态进行预测,涉及到状态、状态转移与马尔科夫过程相应的概念。灰色-马尔科夫模型的创建步骤如下。

步骤1:状态划分。根据灰色MGM(1,1)模型对监测点累计位移量预测值和实测值相对误差序列进行计算,以此划分h个状态区间

Ei=[Ai,Bi](i=1,2,…,i)。

(14)

步骤2:通过状态Ei经过k步到状态Ej转移的次数为nij(k),出现状态次数为ni,那么状态Ei通过k步到状态Ej中转移的概率为

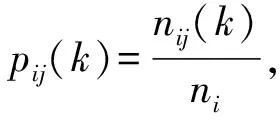
(15)

此模型转移概率和初始状态没有关系,n×n阶状态转移概率矩阵为

(16)

步骤3:h步状态转移概率矩阵为第一步状态转移概率矩阵h次方,也就是

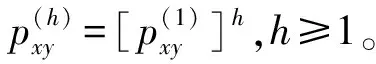
(17)

MGM(1,1)模型没有考虑步数调整、状态转移使模型预测过程满足边坡位移真实情况,使用灰色-马尔科夫模型从而弥补灰色MGM(1,1)的模型问题,降低模型固有误差,使预测精度得到提高,增加了有效预测时间。

4 滑坡发展变化趋势预测

4.1 滑坡变形监测数据

滑坡的变形监测可以掌握滑坡的变形规律,确定滑体位移的速率和方向及其变形所处的阶段,把握潜在失稳滑坡的滑移面,为滑坡稳定性分析和滑坡地质灾害预警提供依据。故浙江省第三地质大队测绘院根据该滑坡地质条件、现状,通过设置监测点、监测墩对表层位移进行监测、并通过深层水平位移监测辅助确定滑带位置。地表位移监测自2019年10月30日至2020年5月30日,采用拓普康MS05AⅡ型全站仪,监测方法为24 h定时全自动跟踪测量,仪器后视归零、前视照准、读数、计算、记录等均为自动完成。监测完成后,监测数据通过合众微程监测软件自动处理后,实时传输至PC终端并及时处理以确保监测数据可靠度。为获得深层水平位移监测数据,在主滑面上的8个钻孔内埋入测斜管,且在埋入测斜管后及时启动监测,保证了监测数据的准确性。在监测方案布置实施过程中,根据现场实际情况,优化调整工作布置,监测点位置见图4。

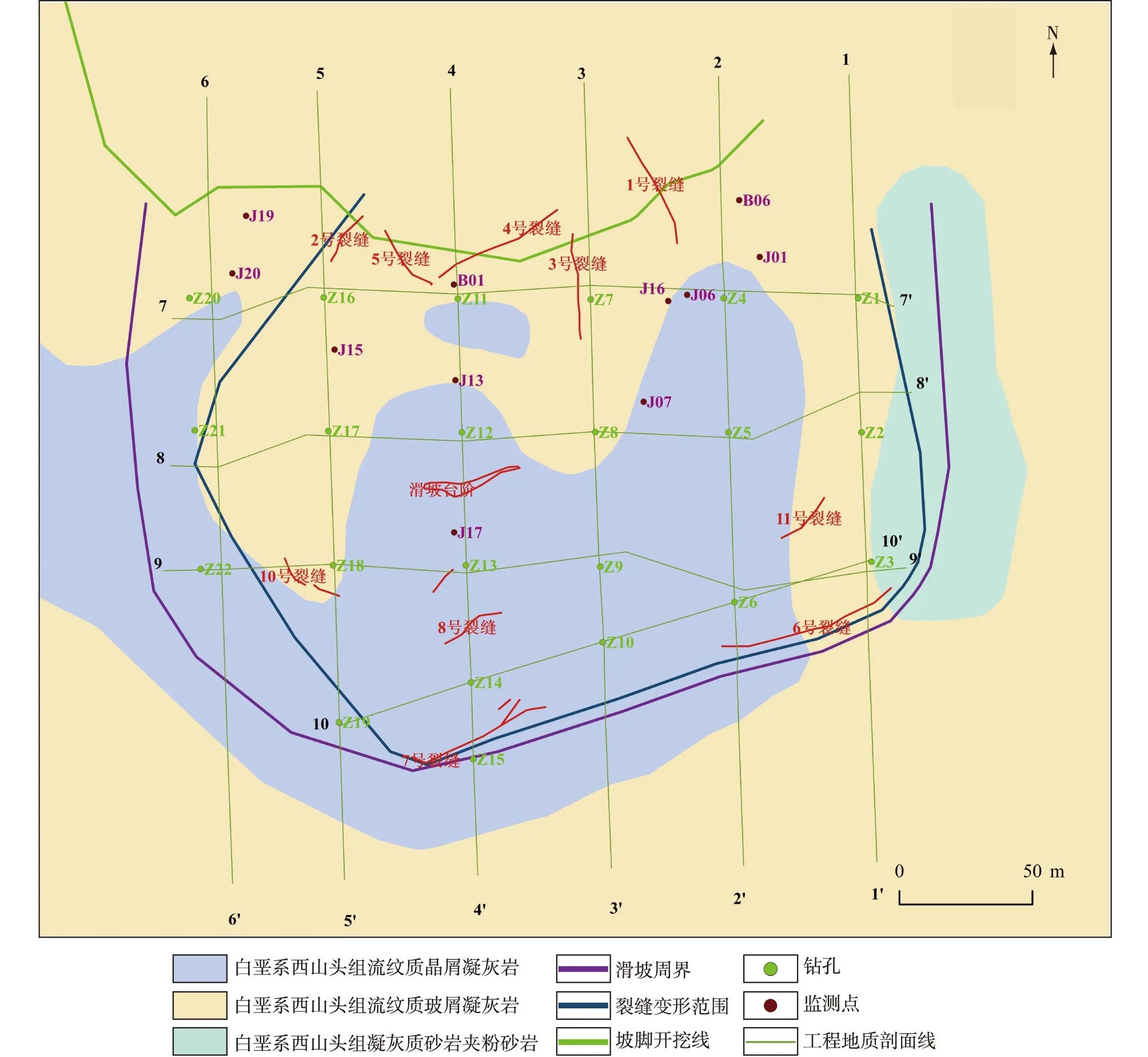
图4 金华市某岩质滑坡监测点平面布置图Fig. 4 Monitoring map of a rock landslide in Jinhua City

由于其中部分监测点在应急处置阶段被破坏,监测数据中断,本文选择较有代表性且监测数据相对完整的J07和J16监测点的监测数据进行分析。以下为2019年10月至2020年5月按月提供的累计变形数据(表1)。

表1 金华市某岩质滑坡累计水平位移(2019.10.30—2020.5.19)

4.2 MGM(1,1)-MC模型预测结果

按照MGM(1,1)模型的建模机理,以J07监测点为例,首先以J07监测点2019年11月份至2020年2月份累计位移作为原始数据测试集,据此建立该滑坡累计位移量序列

x(0)=(199.94,259.77,248.94,311.2),

(18)

作累加生成{1-(AGO)}序列

x(1)=(199.94,459.71,708.65,1 019.85)。

(19)

针对灰色白化方程并进行参数估计,其中参数估计结果如下:

α=(BTB)-1BTY=[-0.098,215.005 1]。

(20)

计算的时间相应序列

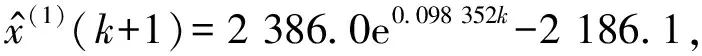
(21)

递推得还原时间响应序列

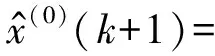
2 386.0e0.098 352k(1-e0.098 352)。

(22)

对该数据序列分别进行提出代谢处理,得到基于MGM(1,1)模型对于该滑坡2019年11月份至2020年2月份累计位移量拟合值,以及2020年3月份累计位移量预测值。具体拟合预测结果及计算累计位移量实测值与预测值的相对误差见表2,并据此进行马尔科夫状态区间划分。

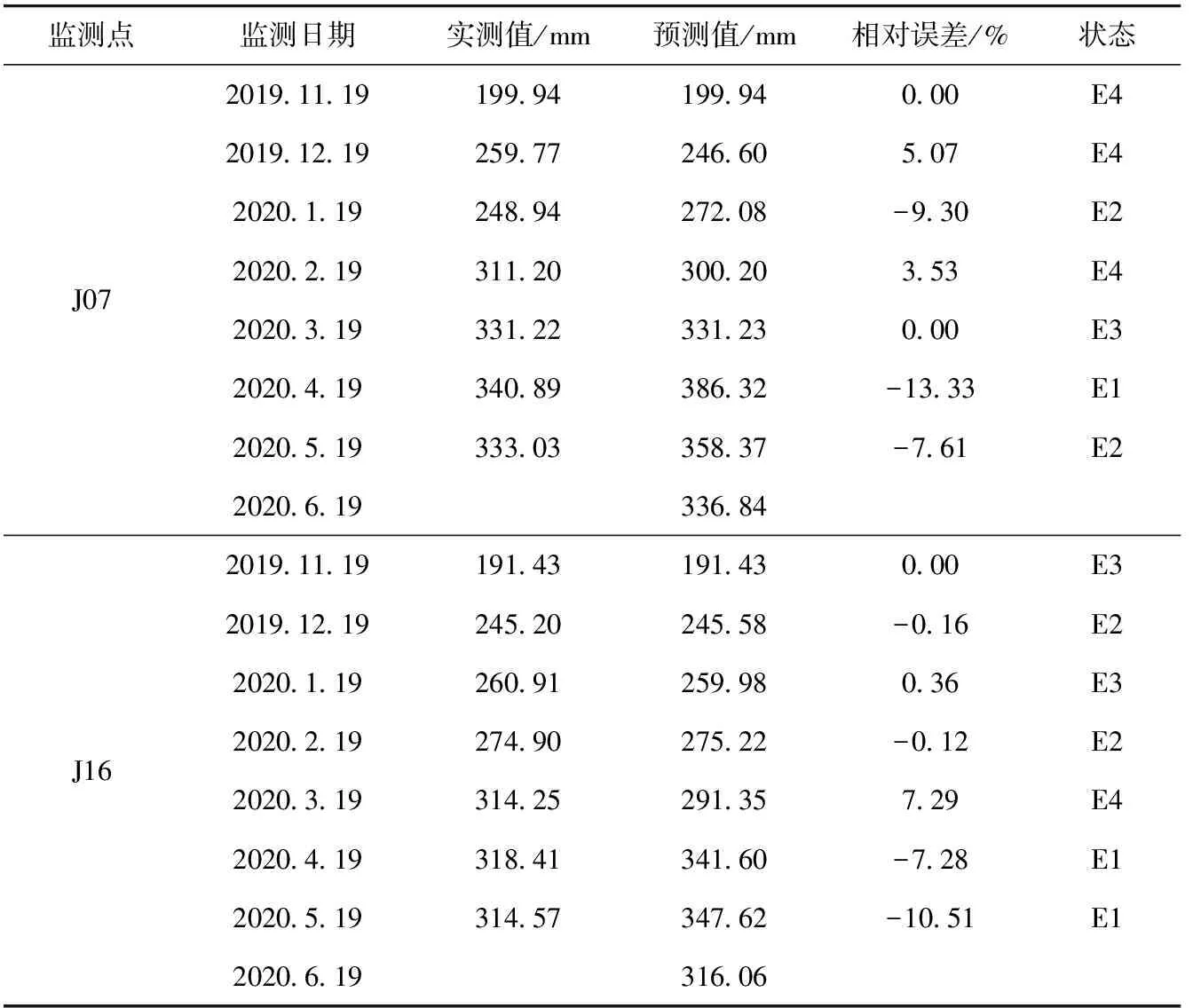
表2 MGM(1,1)模型累计位移量预测值及相对误差

由表2可知:J07监测点累计位移量实测值与MGM(1,1)模型预测值的相对误差最大为5.07%,最小为-13.33%。因此,马尔科夫模型的相对误差范围为[-13,6]。J16监测点累计位移量实测值与MGM(1,1)模型预测值的相对误差最大为7.29%,最小为-10.51%。因此,马尔科夫模型的相对误差范围为[-11,8]。据此将马尔科夫状态分别划分为4个区间(表3)。

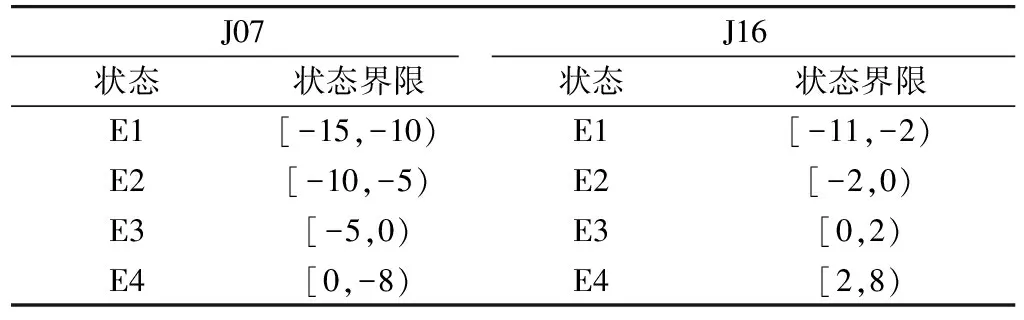
表3 金华市某岩质滑坡状态划分标准

此处以表2中J07监测点累计位移量预测值以及状态划分区间为例,可得到J07监测点累计位移量的1—4步状态转移概率矩阵如下,同理可得J16监测点状态转移概率矩阵:

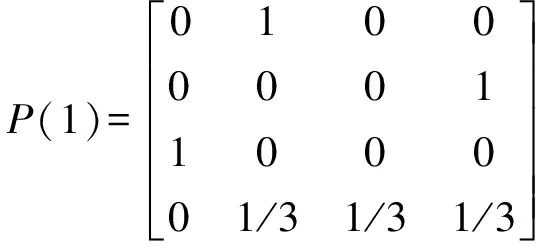
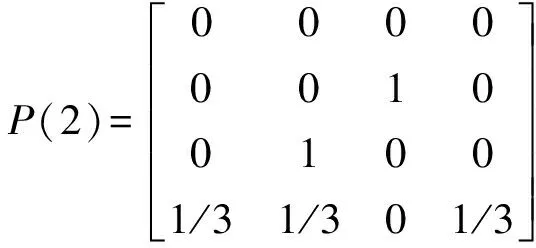
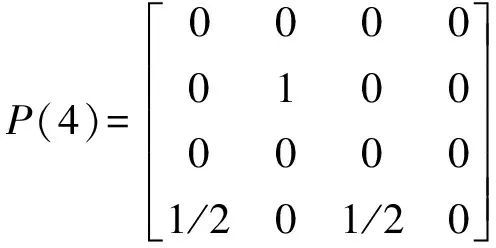
马尔科夫状态划分为4个,故选择距离预测时间(2020年6月19日)最近的4组数据进行预测,在转移概率矩阵中挑选初始状态所对应的行向量组成概率转移矩阵,对相应的新矩阵列向量求和,其中最大值则是2020年6月19日累计位移预测值所对应的状态,如表4所示。

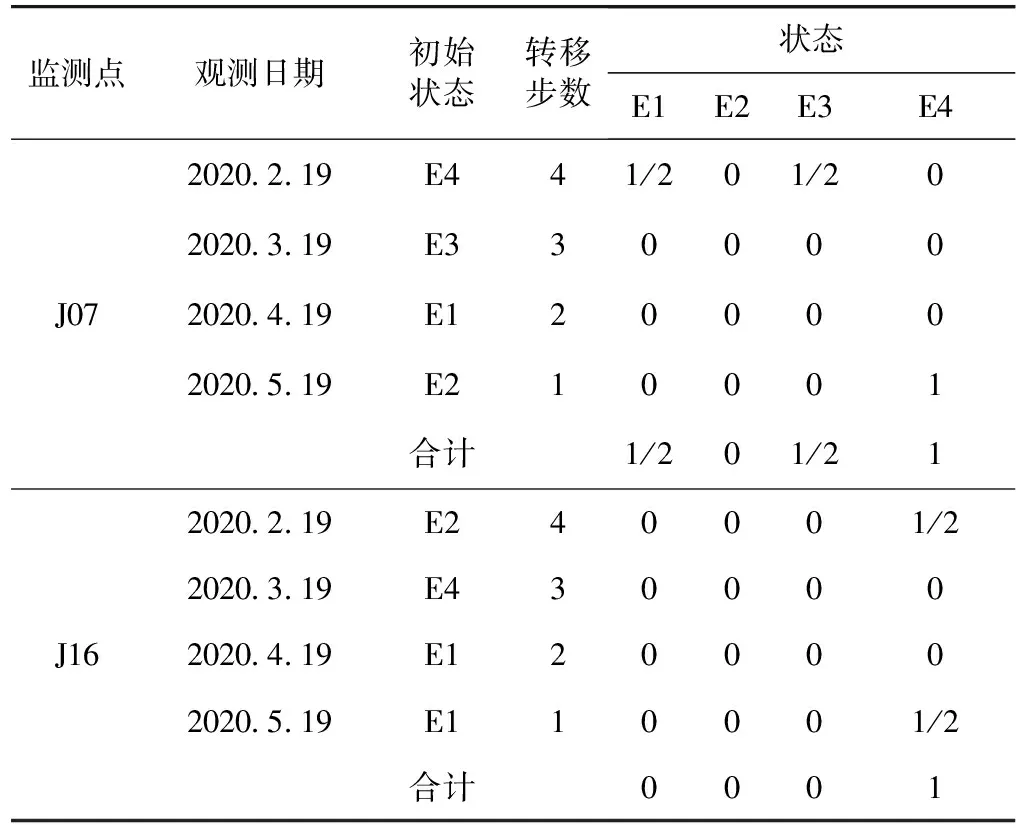
表4 金华市某岩质滑坡状态预测计算结果

灰色-马尔科夫模型充分考虑概率问题的未来发生情况,将灰色理论作为基础提出了修正系数。MGM(1,1)模型2020年6月19日的累计位移量预测值与修正系数相乘即可得出MGM(1,1)-MC模型2020年6月19日的累计位移预测值。

β=1+θ,

(23)

其中,β为修正系数;θ为预测状态区间中值。以灰色-马尔科夫模型的划分原则,使J07误差值划分成为[-15,-10),[-10,-5),[-5,0),[0,-8)4个区间,J16误差值划分成为[-11,-2),[-2,0),[0,2),[2,8)4个区间,表5为各状态下的β值。

表5 金华市某岩质滑坡β值

从表4的合计结果可以看出,J07和J16监测点最大值对应的状态均为E4。监测点最大值对应的状态为状态4。J07和J16监测点MGM(1,1)模型的2020年6月19日位移预测值所处的修正区间分别为[0,-8)和[2,8),是利用状态区间中位数作为未来时刻预测值的相对值,求取修正后的预测值。因此,J07和 J16监测点的MGM(1,1)-MC模型的2020年6月19日位移预测值分别为336.84×1.04=356.31 mm和316.06×1.05=336.87 mm。

4.3 数据结果分析

按照马尔科夫修正过程,分别建立J07和J16监测点MGM(1,1)-MC模型。以Matlab2018软件为平台,编写计算方法的相关程序,并计算2个监测点的累计位移量预测值。J07和J16监测点的3种模型预测结果见表6,3种模型的数据与实测数据曲线比较图见图5、图6。

从表6中可以看出,J07监测点的MGM(1,1)-MC模型的预测值平均绝对误差2.82 mm远小于GM(1,1)模型以及MGM(1,1)模型的预测值平均绝对误差;J16监测点的MGM(1,1)-MC模型的预测值平均绝对误差3.71 mm小于GM(1,1)模型以及MGM(1,1)模型的预测值平均绝对误差;同时,从图5与图6中可以看出,2个监测点的MGM(1,1)-MC模型的数据与实测值曲线拟合效果最好。从2个监测点的预测值可以看出,MGM(1,1)-MC模型的预测值更具参考价值。

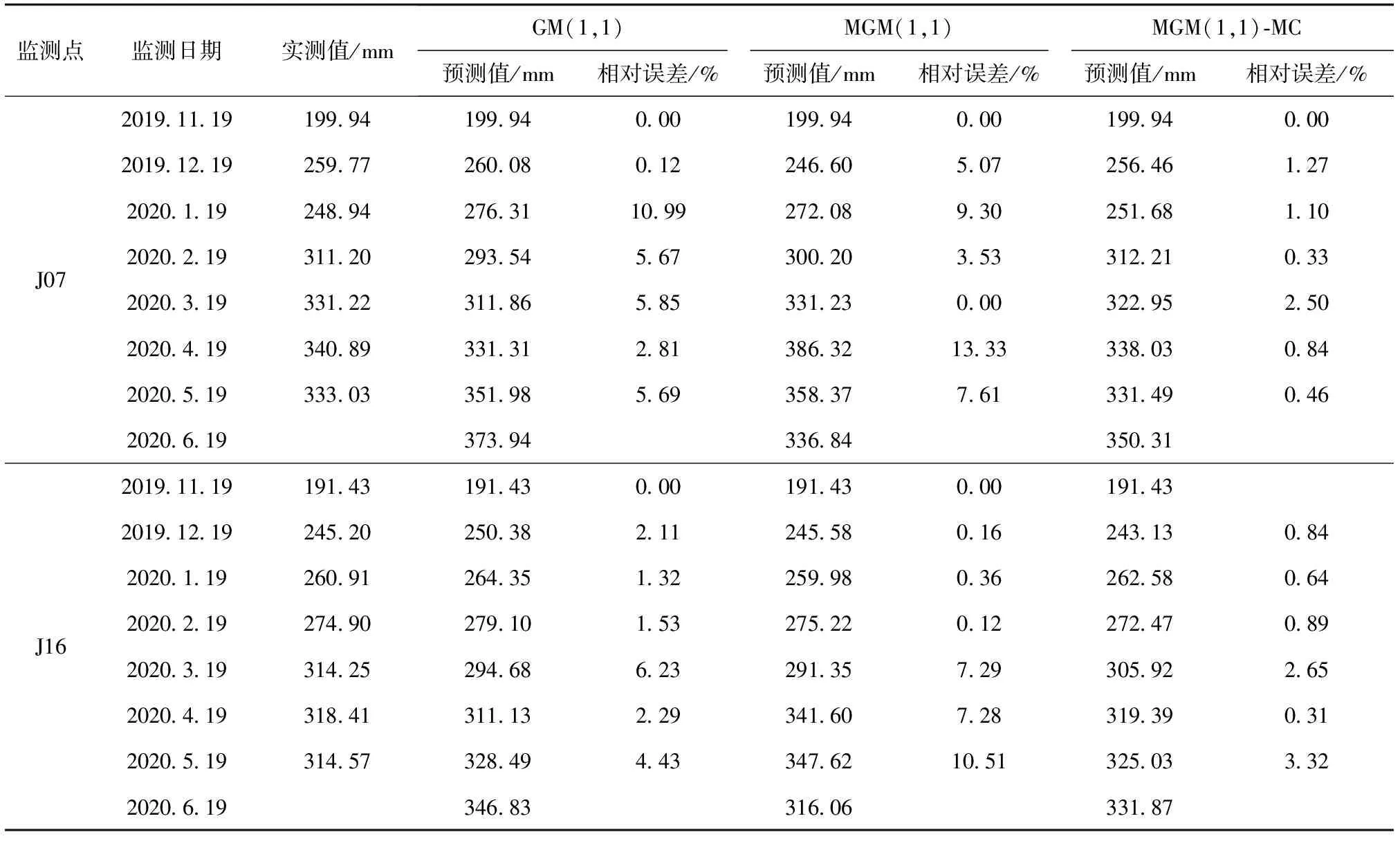
表6 金华市某岩质滑坡3种模型预测结果对比统计结果

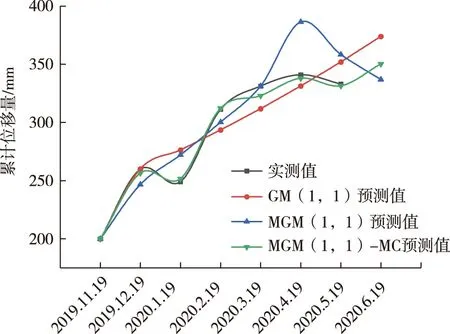
图5 金华市某岩质滑坡J07监测点累计位移量图Fig. 5 A comparison graph of the model predication values and the measured values of the J07 monitoring point of a rock landslide in Jinhua City

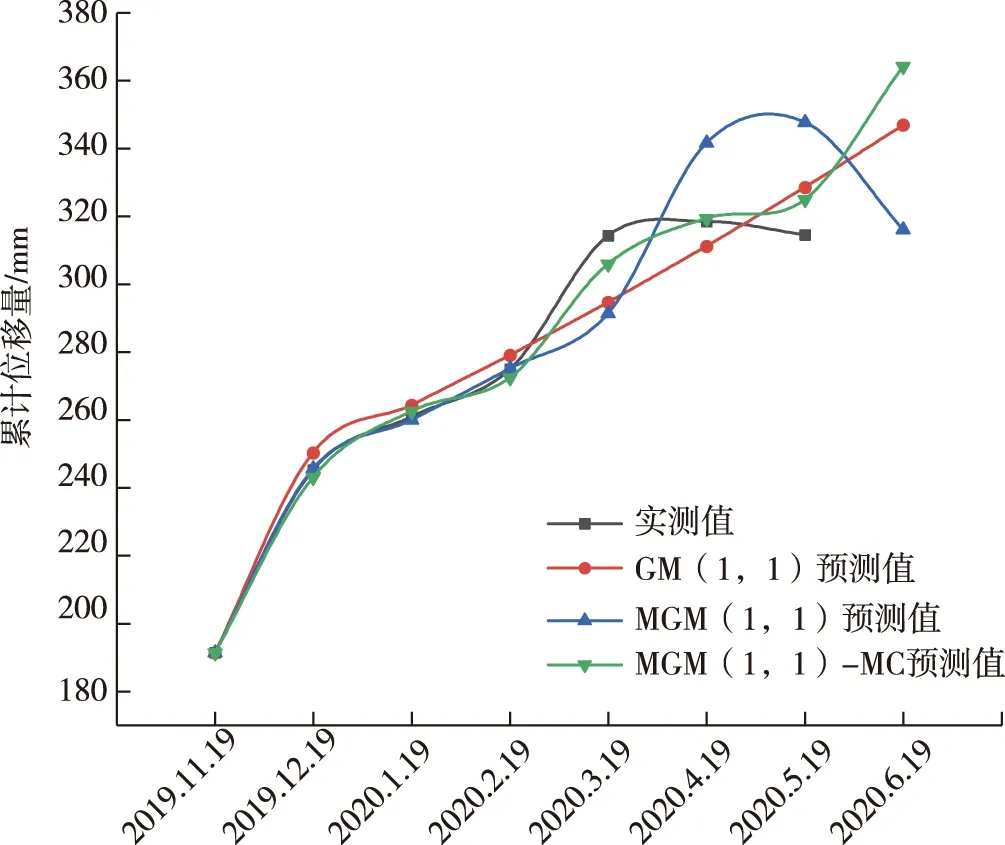
图6 金华市某岩质滑坡J16监测点累计位移量图Fig. 6 A comparison graph of the model predication values and the measured values of the J16 monitoring point of a rock landslide in Jinhua City

4.4 发展趋势预测

根据预测数据可以发现截止2020年6月19日的预测累计位移值依旧在攀升,滑坡趋于不稳定状态。结合实际情况可知,该滑坡在2019年10月19日发生之后,在坡脚做了压脚处置,并在坡顶做了削坡处理,有效缓解了该滑坡体的滑动。依据应急处置阶段的坡面变形监测数据,坡体变形依然存在,整个滑坡体没有达到稳定状态。同时应急处置采取的压脚为松散土体,在暴雨下会逐步滑塌,不能直接作为防护措施使用。因此,滑坡体没有达到稳定,一方面在暴雨天气压脚坡体会滑塌崩解,另一方面降雨会持续地间歇性促使下滑力增大,使滑坡体变形下滑的可能性明显增大,从而有可能演变成二次滑坡,因此实施治理非常有必要。

5 结论

(1)该滑坡成因较为复杂,是固有因素与诱发因素综合作用下的结果,即在内部贯通结构面存在的前提下,由外部因素(如人工切坡、地下水活动等)诱发产生的。

(2)利用马尔科夫理论可以修正预测数据的扰动性,本文将MGM(1,1)模型与马尔科夫理论耦合起来,建立了MGM(1,1)-MC模型,并应用于滑坡的变形监测中。结果表明,MGM(1,1)-MC模型的预测稳定性和精度都要优于灰色GM(1,1)和MGM(1,1)模型预测结果,有效地克服了以往预测模型中信息不关联和因素扰动性大的缺陷。本文建立的MGM(1,1)-MC模型应根据实测数据,及时更新建模数据,用最新的、更可靠的数据建立预测模型。

(3)根据预测数据可以发现截止2020年6月19日的预测累计位移值依旧在攀升,滑坡趋于不稳定状态。已有应急处置采取的压脚为松散土体,在暴雨天气会逐步滑塌,不能直接作为防护措施使用。因此,滑坡体没有达到稳定,在各种因素共同作用下可能会演变成二次滑坡,实施治理非常有必要。