SHALSTAB模型在浙南林溪流域滑坡预测中的应用

孙 强,张泰丽,伍剑波,王赫生,朱延辉,韩 帅

(中国地质调查局南京地质调查中心,江苏 南京 210016)

浙南林溪流域所属的浙闽丘陵山地区是我国群发性滑坡重点防治区之一,多年饱受台风暴雨袭扰。该区域地形起伏大,构造发育,岩体破碎、风化强烈,频发的极端降雨与人类工程活动诱发了大量的地质灾害。尽管滑坡形成和触发的因素是众所周知的,但其发生与诱发因素之间的映射关系仍然是一个巨大的挑战,也一直是地质灾害领域研究的难点和热点[1]。滑坡易发性评价为地质灾害管理提供重要信息,是提升防灾减灾效果的重要措施之一[2]。

国内外对滑坡预测进行了大量的研究,理论方法主要有统计分析模型、确定性模型等。统计分析模型一般较少考虑滑坡发生的内因,注重对影响滑坡的各种因子与滑坡分布之间函数关系进行分析,由于统计分析模型是基于数据进行预测, 因此在一个地区所建立的模型一般不适用于其他地区[3]。确定性模型以物理力学为基础,其各项参数及计算过程有实际的物理意义。在进行区域斜坡稳定性的计算,由于土体的不均匀性,输入参数通常是以点代面,模型的准确性受限于输入参数的数据量和数据精度,输入的参数越多,精度越高,模型与实际情况的吻合度越高,但实际计算过程中,对每个计算的单元进行采样测试是难以实现的,也是不经济的。由于缺乏详细的土体力学参数,该方法通常仅适用于单个滑坡或者小范围区域。但近几年,确定性模型已经由单一的边坡稳定性模型,逐渐发展为能进行区域斜坡稳定性分析的耦合模型。

目前的确定性模型有很多种,如CHASM、SHALSTAB、SINMAP、TRIGRS、SHETRAN、GEOTOP FS和SUSHI等。选择合适的模型对正确认识和预测滑坡有着重要的意义。BATHURST J C等[4]强调用水文空间分布的物理模型来预测滑坡。将水文模型与滑坡稳定性进行耦合是目前被广泛认可的降雨型滑坡预测方法[5]。在这些模型中,浅层滑坡稳定性模型(SHALSTAB)耦合了稳态水文模型与无限边坡稳定模型,模型中的假设条件和降雨因素的考量较符合浙南林溪流域的滑坡破坏模式。

国内许多学者使用SHALSTAB模型进行区域的滑坡预测。同霄等[6]对浅层黄土滑坡的预测研究显示浅层滑坡分布于雨水汇积的区域,与实际情况较吻合。康超等[7]利用SHALSTAB模型进行黄土滑坡预测,模型使用了近70个勘察点的土体力学参数,计算结果显示正确率为70. 23%。王佳佳等[8]依据三峡库区二期和三期滑坡勘察资料,统计了3类滑坡滑体的重度和抗剪强度参数,基于SHALSTAB模型对巴东新城进行了滑坡灾害预测。陈悦丽等[9]通过Monte Carlo法随机生成1 000组土体黏聚力和内摩擦角的值,计算斜坡失稳的概率,模拟结果显示当滑坡危险性阈值取10%时,有90%以上的历史滑坡点落在危险区域内。由于模型中需要的土体力学参数通常需要实验分析获取,如果研究区域面积较大,考虑人力、物力和时间等的成本,并且试验测试本身存在误差,土体力学参数具有高的空间变异性[10]。目前的研究证实,对模型输入的土体力学参数进行合理的取值是非常重要的[11]。

土体的矿物组成对抗剪强度和水理性质有着重要的控制作用[12-13],而土体的矿物组成与其母岩岩性是相关的。对各种地层岩性分布区进行分析测试进而获得该区域土体力学参数,使模型更符合实际情况,同时满足经济和可行性的需求。在考虑到土体力学参数分布不均,基于同种岩性的土体力学参数的概率分布特征进行判断斜坡的稳定性更加合理有效。与王佳佳等[8]、陈悦丽等[9]方法不同,本文模型采用的岩土力学参数为大样本实测数据,在充分分析不同岩性的土体力学参数概率分布特征的基础上,通过SHALSTAB模型进行了林溪流域滑坡预测。

1 研究区概况

研究区位于浙江省温州市中部的林溪流域,横跨瑞安市与瓯海区(图1(a))。林溪流域面积约61 km2,是飞云江下游的一条支流,干流长度8 km左右,流域内溪流纵横,在瑞安市湖岭镇南部上街村汇入飞云江。

流域最高海拔位于北侧瑞安市境内大岩头，海拔为905.4 m,最低海拔位于流域南部的上街村,海拔12.1 m,东侧的五峰尖为瑞安市和瓯海区的界山(图1(b))。流域内山高坡陡、沟窄谷深,上游的支沟水系为源发性溪流,沟谷比降一般100‰～300‰,水流湍急,每年汛期河水位暴涨暴落,常引起溪流塌岸。在林源村一带,林溪被截断,修筑有林溪水库,受水库调蓄作用,下游溪流潺湲,谷地开阔。据多年统计数据,流域全年平均降雨量为1 200 mm左右,降雨集中,7～9月降水量占近全年降水量的70%以上。

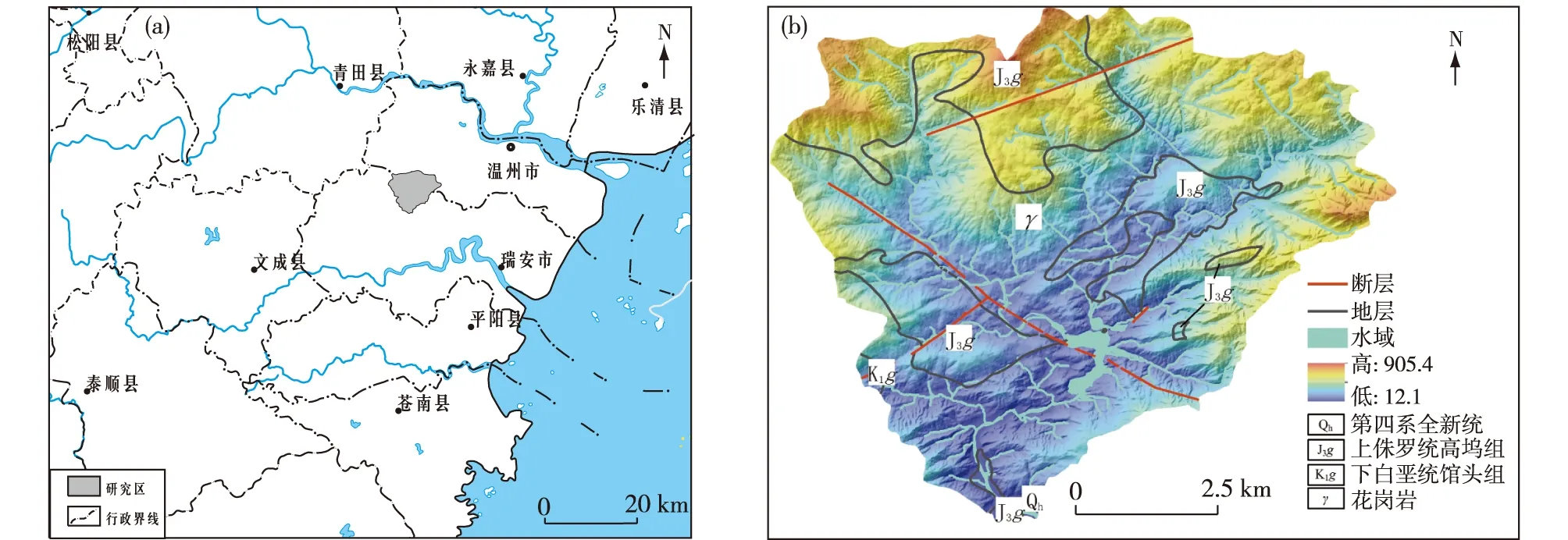
图1 研究区地理位置(a)和地势图(b)Fig. 1 Geographical location(a) and topography(b)of the study area

林溪流域属华南褶皱系,浙东南褶皱带泰顺—祖州断拗的中部。燕山期地质构造-火山-岩浆活动强烈,断裂十分发育,大面积分布火山岩。流域内分布的主要地层岩性有燕山期花岗岩，上侏罗统高坞组(J3g)凝灰岩,下白垩统馆头组(K1g)凝灰岩、粉砂岩等。受构造影响,区域岩体风化强烈,松散层厚度大,为滑坡发育提供了基础地质条件。随着城镇化的发展,区内居民建房、公路建设等大量工程活动产生边坡开挖,并在近年来极端降雨频发的气象条件下,诱发了大量滑坡。2016年开展的1∶1万地质灾害调查成果显示该区自1997年以来,共发育滑坡34处,密度达0.56处/km2。

2 SHALSTAB计算原理

MONTGOMERY D R和DIETRICH W E[14]于1994年提出了SHALSTAB模型,此模型基于莫尔-库仑破坏准则,结合了无限边坡模型和稳态水文模型。

2.1 无限边坡模型

由于研究区内的滑坡规模小,滑面埋深浅,其滑体长度远大于滑体厚度,无限边坡稳定性模型是非常有效的。该模型主要考虑岩土体的下滑力和抗滑力,忽略了边缘效应。无限边坡稳定性的模型是基于莫尔-库仑破坏准则,其修正公式为

ρs·g·z·sinθ·cosθ=c+(ρs·g·z·cos2θ-

ρw·g·h·cos2θ)·tanφ,

(1)

式中:c是土体的黏聚力,Pa;φ是土的内摩擦角,°;ρs是湿土的密度,kg·m-3;z是土体厚度,m;θ是斜坡坡度,°;ρw是水的密度,kg·m-3;h是地下水位,m;g是重力加速度,m·s-2。

2.2 稳态水文模型

滑坡的稳定条件与地下水位直接相关。因此,建立水文模型来估算地下水位是十分必要的。TOPMODEL模型是最常见描述边坡稳态潜流的水文地质概念模型[15],其表达式是达西定律方程的变形方程式

q·a=b·ks·h·sinθ·cos,

(2)

式中:q是有效降雨强度,m·d-1;a是积水面积,m2;b是排水区宽度,m;ks是土体饱和渗透系数(假设沿土层深度是均匀的),m·d-1;h是地下水位,m;g是重力加速度,m·s-2。

根据公式(1)和公式(2)可以建立无条件稳定、无条件不稳定及基于q/T函数关系的SHALSTAB方程组。

无条件不稳定,即土体无地下水时,斜坡仍然无法保持稳定。

(3)

另外一种极端条件发生在h/z为1(完全饱和)时,土体抗剪强度较大,斜坡仍然保持稳定。

(4)

SHALSTAB最终方程为

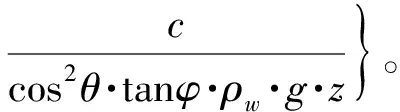
(5)

SHALSTAB模型需要输入的参数为c,φ,ρs和z,其他变量(a,b和θ)从数值高程模型(DEM)提取。SHALSTAB主要是根据有效降雨强度q和土壤的导水系数T之间的比值(q/T)与土壤强度在地形上所能产生的最大饱和状态进行斜坡稳定性的判断。将斜坡分为7个稳定等级,除了无条件稳定和无条件不稳定2个等级外,其他5个等级是q/T的一个函数(按照倍数关系)，表1列出了其他5个等级的q/T断点值。

表1 q/T及log(q/T)换算表

3 输入参数

3.1 地形数据

模型所需的坡度、积水面积等参数均由数值高程模型(DEM)获取。DEM分辨率越高,地图越能清晰呈现真实的流域面积和坡度,但是没有一个“完美”的DEM分辨率可以适用所有地区的边坡稳定性分析[16]。WU S M等[17]发现当其他参数精度有限时,单纯的提高DEM分辨率对评价结果影响很小。考虑其他输入参数的取样密度,模型中使用的DEM来源于浙江省地理信息与测绘局(浙江温州地区2013年测绘成果),精度为5 m。区域内的滑坡几何特征均为实测。通过划定滑坡边界形成滑坡分布图,并用于检验模型效果。在本研究中,所有的滑坡均为发生过或者有明显变形迹象的滑坡。

3.2 土体厚度

土体厚度的获取方法有很多种,一般通过动态圆锥贯入仪测定土体的厚度,也可以通过滑坡体的观测估计土体深度[18]。本文土体的厚度数据源于区域地质灾害调查,调查精度为1∶1万。调查严格按照2014年中国地质调查局颁布的《DD2014—08地质灾害调查评价技术要求(1∶50 000)》[19],调查路线间距一般为300～500 m,调查点密度3.4处/km2。研究区内人类工程活动强烈,有大量的人工边坡揭露了土体的厚度。通过统计有土体厚度调查数据的118个调查点,进行回归克里格插值形成土体厚度的栅格面。结果显示区域内南向坡土体较厚,土体深度最大8.60 m,平均深度为4.01 m左右,随着坡度的升高,土体厚度逐渐变薄(图2)。

图2 土体厚度与坡度(a)、坡向(b)关系图Fig. 2 Relation between soil thickness and slope gradient(a), slope aspect(b)

3.3 土体参数

研究区主要出露3种岩性,分别为粉砂岩、凝灰岩以及花岗岩。沿调查路线均匀布点共采集了208组样品(粉砂岩30组、凝灰岩52组以及花岗岩126组),进行土工试验后,得到了土体的抗剪强度参数、重度、饱和渗透系数和粒径分布。由于研究区滑坡的厚度小,发生破坏速度快,土体的抗剪强度参数(φ和c)通过原状土样的直剪试验测定。3种岩性的抗剪强度参数分布如图3所示:

图3 不同岩性区域土体的抗剪强度参数特征Fig. 3 Parameter characteristics of shear strength of different lithological soil masses

粉砂岩地区的土体c值较高,但φ值较小;花岗岩地区的土体c值较低,φ值较大,且样品间的差异明显(表2)。土体的c值变异系数54.0%～69.2%,而φ值则变化较小,变异系数13.4%～21.9%。

表2 不同岩性区域土体的c、φ值特征

多个研究[20-21]表明土体的黏聚力和内摩擦角呈正态分布。研究区的土体抗剪强度参数的分布也符合正态分布,根据实测值拟合的正态分布曲线参数如表3所示。

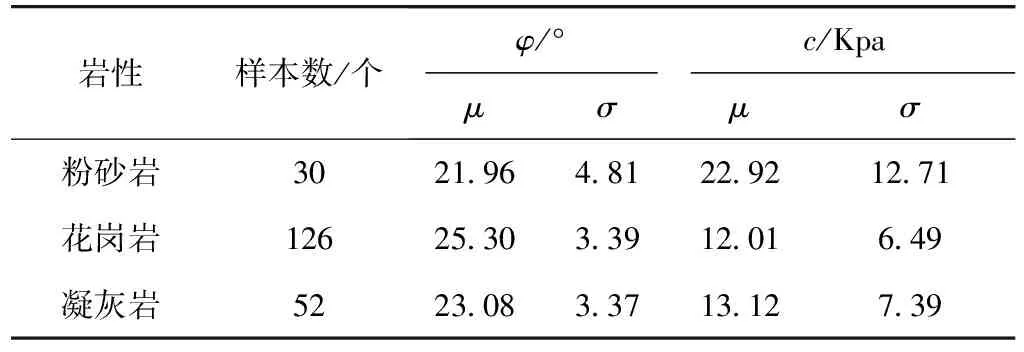
表3 不同岩性区域土体抗剪强度的正态分布参数

模型采用单侧置信区间下限值(置信水平为0.90)进行预测模拟。对研究区土体重度及渗透系数的考虑与土体厚度相同,通过回归克里格插值形成连续的栅格面。

4 讨论

4.1 稳定性结果及评价分析

将公式(3)、公式(4)、公式(5)计算结果进行叠加，计算各单元的稳定性指数,按照表1进行重分类后得到稳定指数分级图(图4)。

图4 稳定性指数分级图Fig. 4 Stability index map

模型结果显示,研究区不稳定的区域较连续,主要位于斜坡的下部及深切河谷的两侧且坡度陡峭的地区。无条件稳定的区域占研究区总面积的68.10%,主要为山体顶部,土体厚度薄及地形平坦的区域。

4.2 模型质量评价

模型质量通过评估实际发生的滑坡与预测滑坡之间的空间重合来实现的,SORBINO G等[22]提出捕获率(SI)和误判率(EI)两项量化指数能有效检验模型质量(图5)。SI指的是模型预测滑坡区域与实际发生滑坡重合区域占实际发生滑坡区域的百分比,而EI是模型预测滑坡区域占实际未发生滑坡区域的百分比。

(12)

(13)

SORBINO G等[22]发现模型中输入不同的参数,预测结果的SI值与EI值均发生变化,但两者之间呈线型相关, SI/EI比值具有更好的评价模型效果,比值越高说明模型的预测效果越好。用2016年开展的林溪流域1∶1万地质灾害调查获得的实际滑坡数据作为验证,不同log(q/T)水平为不稳定区判别标准的SI值与EI值如表4所示。

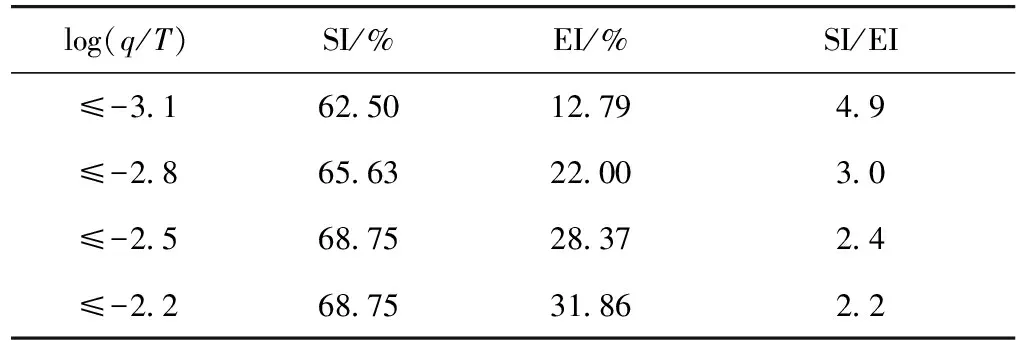
表4 不同log(q/T)水平的量化指数

随着log(q/T)水平的提高,模型预测的滑坡面积逐渐扩大,SI值逐渐增大, EI值同时增大, SI/EI值由4.9减小到2.2。单纯提高log(q/T)水平,滑坡与预测滑坡之间的空间重合度增大,同时导致未发生滑坡的区域内,预期滑坡的面积增大,误判率升高。log(q/T)≤-3.1时,量化指数的SI/EI值最大,作为预测滑坡判别标准是较恰当的,滑坡预测与实际情况有较高的重合度,保持较低的误判率。以此为标准时,滑坡预测的捕获率为62.50%,误判率为17.79%。

5 结论

(1)研究区土体的抗剪强度参数符合正态分布,c值表现出较大的空间差异,变异系数54.0%～69.2%,而φ值变化较小,变异系数13.4%～21.9%。3种岩性分布区土体的抗剪强度参数不同,粉砂岩地区的土体c值较高,φ值较小;花岗岩地区的土体c值较低,φ值较大。

(2)模型预测的不稳定区域较连续,主要位于斜坡的下部及深切河谷的两侧,且坡度陡峭的地区,地形坡度以及土体厚度对模拟结果影响较大。无条件稳定的区域占研究区总面积的68.10%,主要为山体顶部、土体厚度薄及地形平坦的区域。

(3)量化指数分析显示随着log(q/T)水平的提高,模型预测的滑坡区域逐渐扩大,SI值逐渐增大, EI值同时增大, SI/EI值由4.9减小到2.2。单纯的提高log(q/T)水平,随着滑坡与预测滑坡之间的空间重合度增大,会导致预期滑坡的面积增大,误判率升高。

(4)以log(q/T)≤-3.1作为预测滑坡的判别标准,量化指数的SI/EI值最大,预测效果较好,真实的捕获率为62.50%,误判率较低,为17.79%。