白噪声激励下非线性声学超材料的随机响应1)

王晓敏 冯进钤 陈越超

(西安工程大学理学院，西安 710048)

噪声充斥在各个领域中，带来了很多负面的影响[1-2]。针对噪声的控制，传统的隔声材料，如钢板、砖墙、多孔和纤维等材料只具备在中高频范围吸附噪声的能力，加之材料的面密度较大，重量过重，仍有很多不足之处。近年来，人们根据实际需要设计出的声学超材料(acoustic metamaterial， AMMs)[3-4]作为一种复合型新型材料，由于制作成本较低，结构简单，具有良好的低频噪声阻隔能力，引起了学者的广泛关注。目前对于线性声学超材料的研究已经比较成熟，对于非线性声学超材料还处于初级阶段[5-6]。Zhao 等[4]提出的单稳态声学超材料通过引入磁场来消除噪声，实现了深亚波范围内宽带低频噪声的吸收，为噪声的控制提供了新的方向。

随机因素和非光滑因素[7]通常会伴随发生，噪声是一种很常见的随机激励，会引起系统产生很多复杂的非线性动力学行为[8]。因此，对于随机振动的响应研究显得尤为重要[9-10]。近年来，解决概率响应的方法有很多种，随机平均法[11-13]由于简单可行，已被广泛使用。针对非光滑碰撞振动系统[14]的研究，学者们通常使用Zhuravlev–Ivanov 非光滑变换[15]。本文的创新点在于单稳态吸收器系统引入了一种对称的非光滑变换，即Galerkin–Ivanov 变换[16]分析系统的响应。并且，将力学和声学领域结合起来进行研究，完善了声学超材料理论。单稳态模型从频域到时域的转化，以及非光滑非线性因素的作用均是富有挑战性的工作。本课题针对噪声作用下的非线性单稳态声学超材料，分析其存在的动力学行为具有重要意义。

首先，通过对单稳态吸收器模型动力学方程的参数做无量纲化处理后和约束条件构成本文的动力学系统。然后，利用非光滑变换得到原系统的近似等效系统。再次，对等效系统做能量包线随机平均得到平均福克普朗克柯尔莫哥洛夫(Fokker Planck Kolmogorov，FPK)方程，再利用非光滑逆变换得到响应的概率密度函数(probability density function，PDF)。最后，通过数值仿真分析系统的随机响应，验证解析结果的正确性。

1 单稳态吸收器的碰撞振动模型

考虑单稳态吸收器的振动模型，如图1 所示。

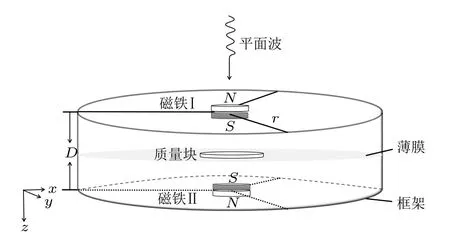
图1 单稳态吸收器

其中参数r表示吸收器的半径。该模型是底部封闭的空腔，它主要由腔体中间薄膜上的质量块和同轴两侧极板上对称放置的一对外部磁铁组成，磁铁会对质量块产生吸引力。该模型在时间域上满足的动力学方程为

考虑单边刚性约束的无量纲化方程为

式中，a，b分别表示刚度和阻尼系数，属于线性项系数；c表示非线性系数。g是与时间相关的变量，它们分别表示为

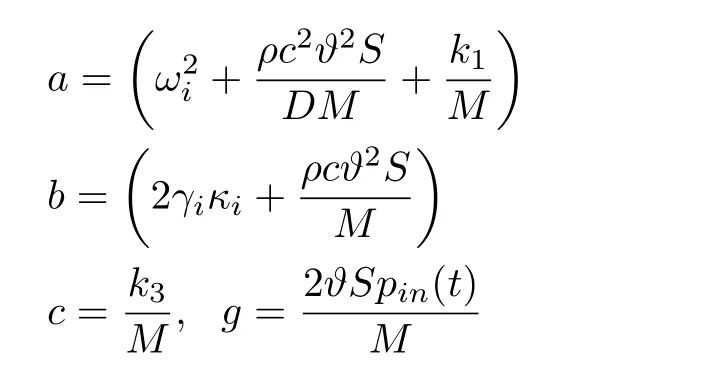
f是噪声幅值，ξ(t) 是标准高斯白噪声，其均值和方差分别满足

τ是表示时间的平移，δ(t) 表示狄拉克函数。

考虑带有单边约束非线性单稳态吸收器的动力学系统，其原始方程可表示为

式中，R是碰撞恢复系数，R的取值大小和碰撞面的材料相关且R ∈(0，1]。可以发现，当R ∈(0，1) 时，碰撞后系统会有能量的损失，R越小能量的损失越大；当取临界值R=1 时，能量不变，系统运动的状态会变得不连续，此时称作未扰系统。˙x-和˙x+分别表示碰撞前后的速度，当x ＞0，系统处于连续运动的状态，可以视作“无约束的”；当x=0，系统处于碰撞约束的位置，所以式(4) 可以看做连续微分方程和碰撞项构成的混合系统。直接求解这个混合系统的解很难，所以需要构造它的近似等效系统。

2 伊万诺夫非光滑变换

为了应用Galerkin–Ivanov 非光滑变换，以状态空间的形式重新构造了方程(4)，引入新的变量m和n。令m=x和n= ˙x，得到

3 概率响应

式(9)给出的是Stratonovich 方程，根据随机微分方程(stochastic differential equation， SDE) 的知识，可以得到其等价的Itˆo型SDE 为

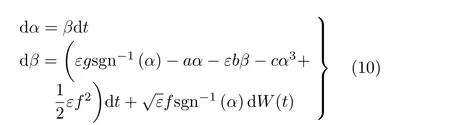
W(t) 是维纳过程。引入小参数ε，εf2/2 表示两种积分变换的Wong–Zakai 修正项。g相对参数a，b，c的取值量级很小，可看做是系统的微小扰动。当ε= 0 时，未扰系统的总能量函数(能量包线) 和势函数分别为

为使能量函数可以取正值，所以G(α)＞0。由Khassminskii 定理可知，H是慢变量，位移变量α和速度变量β是快变量。得到总能量H关于时间导数的微分方程为

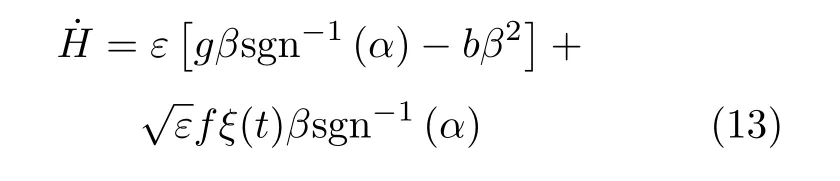
利用式(11)和式(13)结合Itˆo公式，当ε →0 时，H可以用Markov 过程来近似

利用式(11)和式(12)的变换，得到位移变量α和速度变量β的联合PDF

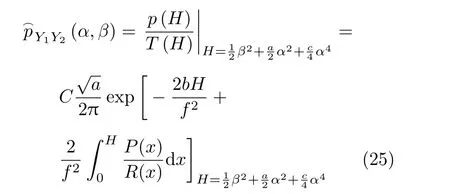
借助非光滑变换式(6) 和式(7)，经过坐标变换可以得到原位移变量m和速度变量n的系统响应的PDF 为

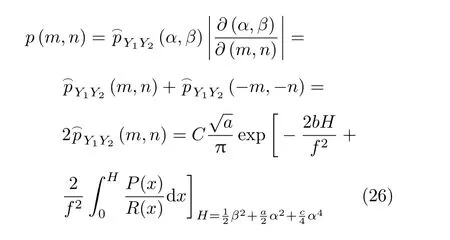
那么，变量m和n的边缘概率密度p(m) 和p(n)分别为

最后，给出能量函数H的解析解p(H) 和相应的数值解˜p(H)，可以计算出系统能量曲线拟合的误差δ(H)，即

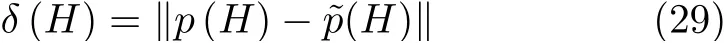
4 数值仿真

将解析解和数值解绘制在同一图中，以验证解析结果的有效性。另外，进一步对数据拟合的误差δ(H) 做相应的分析。

4.1 响应分析

本节分成两个部分，主要讨论通过调节不同的阻尼系数b和幅值参数f，探究对响应PDF 的影响。

4.1.1 系统阻尼变化的响应分析

给出参数c=0.01，f=0.3，g=0.001，固定幅值f，观察取b= 0.03，0.05，0.07 时，系统能量H的函数p(H)、位移m的概率密度p(m)、速度n的概率密度p(n) 以及它们的联合函数p(m，n) 的解析解和数值解拟合的效果，如图2 和图3 所示。其中AS 表示解析结果，NS 表示数值结果。

图2 不同阻尼系数下的PDFs

图3 位移和速度的联合PDFs

图2(a) 给出了H的PDF 曲线。当f固定时，阻尼系数b是引起系统能量损失的重要因素。b取值越大，H的峰值也越高，能量函数p(H)接近于0 的速度越快。这符合熟知的物理背景，阻尼越大，能量损耗会更多，衰减的速率也就越快，结论是一致的。

图2(b) 表示变量m的PDF 曲线。位移曲线是一条截断曲线，它的稳态概率密度变化的峰值是在m= 0 处，即碰撞约束的位置。固定f，增大阻尼系数b，峰值越高，系统的状态处于平衡位置的概率越大。而且，通过将解析结果和Monte Carlo 拟合效果进行比较，发现靠近峰值附近，数值解略高于解析解，这是因为碰撞时刻t0是通过二分法来取值的，通过减小步长使得结果更加精确。

图2(c) 是速度n的PDF 曲线。从图中可以看出，它是一条类似于标准高斯分布的光滑曲线，并且关于中点左右对称。曲线的峰值出现在n= 0 位置，f不变，增大参数b，概率密度曲线的拖尾减小，峰值增高，变得更加陡峭。这表明，阻尼越大，系统更趋向于稳定在平衡位置。减小参数b，峰值降低，曲线变得更加平滑。

4.1.2 噪声幅值变化响应分析

类似地，取系统参数分别为b= 0.05，c=0.1，g= 0.001，固定参数b取值，当f= 0.2，0.3， 0.4 时， 获取不同噪声幅值下系统对应的p(H)，p(m)，p(n)，p(m，n) 的拟合曲线，如图4 和图5 所示。

类似于图2，图4(a)～图4(c) 分别给出总能量H，位移m和速度n的解析和数值结果曲线。当阻尼b一定时，随着幅值f增大，峰值变得越来越低，曲线更加光滑平缓，这表明噪声的扰动使系统容易偏离平衡状态，而且发现p(n) 峰值接近于p(m)峰值的一半，说明噪声会使系统向着远离平衡位置的方向去振动。反之，噪声幅值越小，峰值会逐渐增高，系统接近0 的概率也就越大。可以看到，噪声幅值和阻尼变化对系统的影响是恰好相反的。

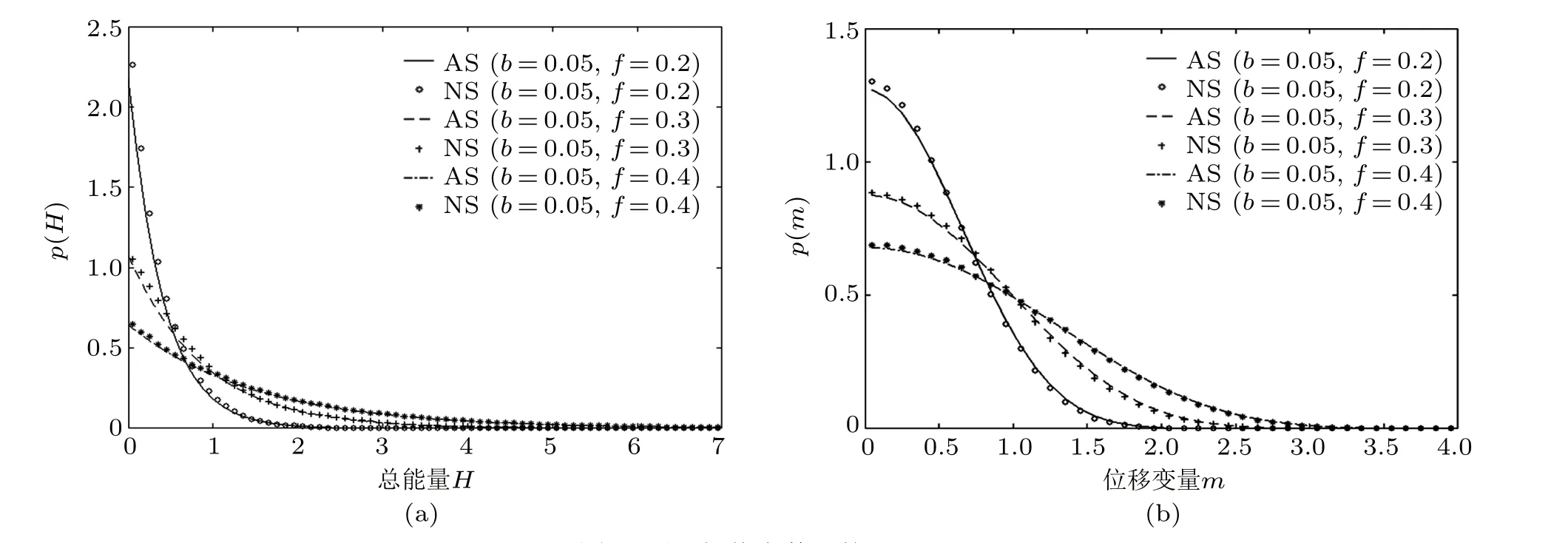
图4 不同幅值参数下的PDFs

图4 不同幅值参数下的PDFs (续)

参照图3，图5(a)～图5(c) 给出的三组图分别表示当f=0.2，0.3，0.4 时，固定b，改变幅值f大小，对比解析解和数值解，可以看到数据拟合的效果很好。

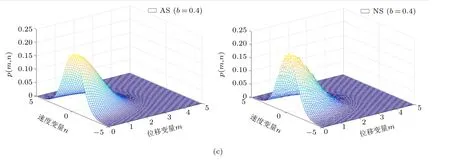
图5 位移和速度的联合概率密度曲线PDFs (续)

4.2 误差分析

给出能量函数的误差曲线来说明使用能量包线随机平均法分析系统响应的有效性。

图6(a)和图6(b)分别给出了不同阻尼系数和幅值参数下，能量H的误差变化示意图。可以看到，通过均方误差的数值模拟，最终误差的阈值小于0.1。随着H增加，误差逐渐减小并逐渐趋于0。伴随阻尼的增大，误差趋于0 的速度加快。结合图2(a) 以及图4(a) 曲线拟合的情况，完全验证了这一点。

图6 能量的误差示意图

5 结论

本文主要研究在刚性约束条件下的非线性单稳态声学超材料吸声器模型的平稳响应。通过引入一种对称的非光滑变换来处理碰撞引起的非光滑位置，给出近似等效系统。然后利用随机平均法获得稳态的PDF，通过解析解与数值解的比较，验证了随机平均法的适用性。结果表明：随机平均法可以有效地分析系统的随机响应。随着噪声幅值的增大，响应的平稳PDF 会变得更加光滑，系统更趋向于稳定在平衡位置。正是由于单稳态声学超材料宽带低频吸声、减振、降噪的优点，结合对其动力学行为的分析，可以给生活、工业、军事等各个领域噪声防控带来极大的便利。基于单稳态声学超材料，本文重点给出了随机响应的研究结果，后续将进一步考虑材料的非线性和噪声特性，探讨强非线性和不同噪声对系统的频幅、模态等方面的影响，提高超声材料的吸音效果。