半正则图的Estrada指数的界

张 宁，张海霞，杨斌鑫

(太原科技大学 应用科学学院，太原 030024)

本文基于文献[1]的结论和证明方法，通过优化简单图和二部图的Estrada指数的界，得到连通图和连通二部图的Estrada指数的界，得到半正则图的Estrada指数的界。最后讨论了Estrada指数的若干应用。

1 背景知识

1.1 研究现状与研究意义

研究现状：Estrada指数提出后，引起了数学工作者的关注.研究者试图通过建立Estrada指数与图的结构参数之间的联系，刻画图的结构性质。本文研究Estrada指数的界，对界进行估计。

研究意义：Estrada指数应用广泛，具有较高的理论意义和实际价值。

1.2 相关定义

简单图：图既没有环也没有两条边连接同一对顶点。

连通图：若G只有一个分支，则称G是连通的。

二部图：图的顶点集就是分为两个子集X和Y，使得任意一条边都有一个端点在X中，另一个端点在Y中。

k正则图：若对所有v∈V，有dv=k.

半正则图:每个顶点的度是r1或r2的二部图，且任一边连接的是度为r1和r2的顶点。

(n，m)图：n个点，m条边的图。

邻接矩阵：表示点与点相邻关系的矩阵。

1.3 Estrada指数的性质

A(G)表示G的(0，1)邻接矩阵[1]，A(G)的特征值，构成了G的谱.n个点的图有n个特征值.图的特征值定义为λ1，λ2，…λn，并且按递减序列排列：λ1≥λ2≥…≥λn.

2000年，E.Estrada在文章中最先引入Estrada指数。定义为:

(1)

称为Estrada指数。

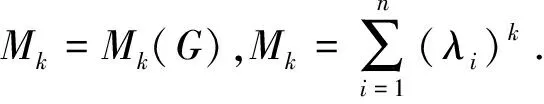
(2)

从文献[2]中，Mk(G)等于G的长为k的圈的数量。

性质2：如果G是二部图，n0是特征值0的重数，

(3)

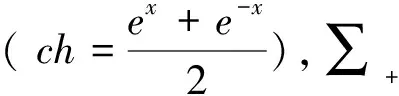
2 一些特殊图的Estrada指数的界

文章的前两个定理的下界，算到三阶谱矩。为了提高下界，利用正确的猜想。

猜想1：在n个点的连通图中，路有极小Estrada指数。

该猜想是由文献[3]的作者提出并给出证明。

M4=14+6(n-4).

(4)

2.1 连通图的Estrada指数的界

引理1G是一个(n，m)简单图。G的Estrada指数的界是：

等式两边成立的条件都是G是一个n个点的空图。

定理1G是一个(n，m)连通图，

证明：为了证明该定理，经常使用一些已知的(n，m)图的阶矩，

M0=n;M1=0;M2=2m;M3=6t;

M4=14+6(n-4).

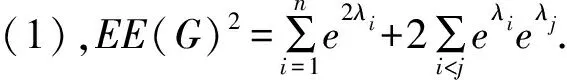
交叉项：应用算术几何平均不等式，

n(n-1)(eM1)2/n=n(n-1).

平方项：利用幂级数展开式，使用M0，M1，M2，M3，M4，得到:

联立两个结果，开平方得到:

上界：从等式(2)开始：

2.2 连通二部图的Estrada指数的界

引理2[1]G是一个(n，m)二部图.G的Estrada指数的界是：

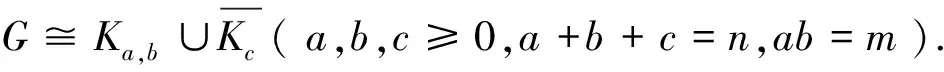
定理2G是一个(n，m)连通二部图。G的Estrada指数的界：

下界的证明如定理1，用n+来定义G的正特征值的个数。二部图的特征值关于原点对称，n0+2n+=n.

上界：

EE=n0+eλ1+e-λ1+eλ2+e-λ2+…+eλn++e-λn+

i=1，2，…n+

3 半正则图的Estrada指数的界

3.1 结果一

引理3[1]G是一个度为r的n个点的正则图.G的Estrada指数的界是：

er+

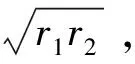
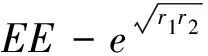
上界：

下界:

平方项：

交叉项：

联立这两个结果，开平方、移项得到下界。

3.2 结果二

引理4[1]G是一个度为r的n个点的正则二部图.G的Estrada指数的界是：

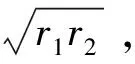
上界：

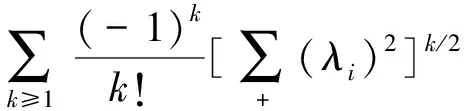
下界：

平方项：

交叉项：

(n-2)(n-3)

联立以上两个结果，开平方、移项得下界。

4 结束语

本文获得连通图和连通二部图的Estrada指数的界，并得到二个半正则图的Estrada指数的上下界.Estrada指数应用十分广泛，用于量化长链蛋白质分子的折叠度[4-6]、提供了一种找到复杂网络核心的手段、拓展的原子分支[7-8]等。