基于多元数据融合的风机故障预警

国电电力河北新能源开发有限公司 孙立志 王 健 赵 鹏 马亚楠

由于风力发电可以做到节能减排，因此世界各国出台了许多风电相关政策，风场效益每年的增幅维持在20%左右，同时越来越注重海上风电的发展，能源供给不足与环境破坏严重是我国目前较为严重的问题，风力发电清洁环保，资源丰富可以长期使用，大力发展风力发电可以解决上述问题[1-2]。随着风电场的规模和风机的数量均不断增大，部分装机时间较早的风机，不断增加的故障次数，也造成了发电效率的下降，如何采用采集到的多元数据对机组故障进行故障预警和判断具有十分重要的现实意义和价值。

近年来我国对风电发展的期望值越来越高，2013～2020年中国风电装机容量（万千瓦）分别为7652/9657/13075/14747/16400/18426/20070/2 3585，全球风电装机容量（吉瓦）分别为312/362/421/473/522/568/612/674。风电系统工作人员通过SCADA 系统获得关于风机故障的多元数据可以反映出风机的发电性能和运行状态，对多元数据进行发掘并加入人工智能等手段对风机进行故障预警与发电性能评估势在必行。

发电机组运行工况恶劣，风机长时间工作在这种环境下其各个部件性能会之间下降，当下降到一定程度时风机便会出现故障，随之影响到风机发电效率。使风机运行的关键部位有轮毂，浆距系统，齿轮箱，发电机，偏航系统等，其中浆距系统与偏航系统主要使风机能最大化的获取风能，从而提升发电性能，制动系统，传动系统，齿轮箱与发电机主要可以将风产生的机械能转化为电能，从而输入电网，塔架的主要作用是撑叶片和机舱。

1 基于ReliefF-PCA 和DNN 的运行风机故障诊断

1.1 风机诊断算法分析

基于已有的风机全息化状态监测系统和SCADA记录，针对风机运行技术数据量大，在故障诊断时有一定困难，在此提出了一种基于ReliefF、主成分分析（PCA）与深度神经网络（DNN）的风机故障诊断方法。首先，对故障相关特征进行提取，使用ReliefF 方法选择与故障相关的特征，降低数据维度；并使用PCA 算法进一步对数据进行降维，降低数据间的冗余性，提高故障诊断的准确性；最后使用优化后的DNN 建立多故障诊断模型。风机故障诊断流程为：数据预处理；数据降维；故障诊断。

1.2 算法数据来源及降维

SCADA 系统记录并存储的大量风机数据，如不对数据进行处理，则会产生故障判断时间长且准确率低的问题，因此需要进行数据挖掘，提取故障数据的敏感特征。主成分分析（PCA）是一种较为常见的特征降维算法，主成分分析（PCA）是一种较为常见的特征降维算法，通过PCA 可以降低特征集的维数，并且仍包含数据的原始信息。

算法流程如下：将矩阵x 集中起来（去掉每个维度的平均数）：C=VTx，计算样本的协方差矩阵：，把协方差矩阵的特征值分解，选取前n 个最大的特征值对应的的特征向量构成特征向量矩阵W。其中：x 为特征向量；V 为去平均化向量；C 为降维矩阵；S 为样本数；Ψ 为特征矩阵中数值每列平均值后的新矩阵；ψ 的协方差矩阵定义为B。

PCA 保留了原始数据中较为重要的内容并且让数据的维度降低，并且数据映射到新空间中使坐标系发生变换，减少了数据间的相关性。ReliefFPCA 算法具体流程为：第一步使用ReliefF 算法对原始SCADA 数据进行特征选择，第二步将数据带入初始化后的ReliefF 算法，第三步将数据输入到PCA 算法中进行特征降维，将90%以上主成分的数据最为最终的输入数据。将隐层数量多的神经网络称之为深度神经网络（DNN），将神经网络的输入得到权重求和后输入到激活函数中，通过激活函数得到下一层的输出。目前在学术界与工程上使用最为广泛的激活函数有sigmoid、tanh、ReLU。

DNN 故障诊断模型搭建具体流程为：

第一步根据数据的来源风机情况，将通过ReliefF-PCA 降维后的数据赋予标签，构建出故障诊断数据集，以6：1：3的比例划分为训练集、测试集、验证集，使用训练集完成对模型的训练，通过测试集调整模型超参数，最后使用验证集验证模型性能；第二步初始化模型参数，包括隐藏层层数、隐藏层神经元个数、激活函数、优化函数、指定输入输出的神经元个数等。

第三步通过训练集训练模型，当达到迭代次数后模型训练完成，此时神经元之间的权重固定，通过分类器softmax 输出结果，权重最大的就属于哪一类，分类器softmax 的loss 函数如为Loss=∑yilnai；第四步通过测试集的loss 曲线进行参数调整，调整到效果最佳后使用验证集验证模型效果。

2 算法模型算法与仿真分析

数据来源：试验数据均采用某风场场数据，数据间隔为10秒钟记录一次，风机选择5台风机，2018年11月其故障次数分别为98/207/296/517/172，发生故障时风机状态由0变为1，将故障最少的2号风机作为正常风机，剔除故障时间段后的数据为正常数据。本文主要对风机几种常见故障进行诊断，分为5种状态：正常状态、齿轮箱油温超温故障、齿轮箱NDE 端轴承温度超温故障、主轴刹车抱闸故障、机舱温度故障。

特征降维与优化：原始数据量庞大，各参数之间相关性高，对原始数据进行特征降维就变的十分必要。对阈值大小进行讨论，分为平均值、中位数与标准差。将A1称为平均数为阈值进特征选择后的特征，A2称为中位数为阈值进行特征选择后的特征，A3称为标准差为阈值进行特征选择后的特征，对应于不同阈值的所选特征数量如表1所示。

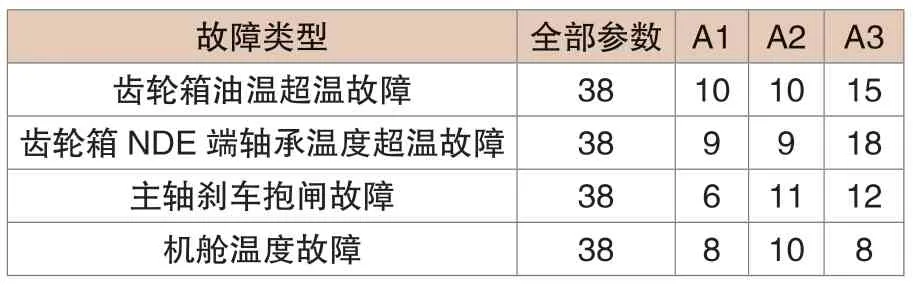
表1 对应于不同阈值的所选特征数量

DNN 优化算法选择：在DNN 中参数的更新算法一定程度影响着网络的训练速度以及诊断准确率，对于这个缺点，提出了许多较为新颖的优化器：RMSProp 优化器、Adagrad 优化器、Adadelta优化器，Adam 优化器。优化算法训练误差中，Adagrad 优化算法收敛速度最慢，并且收敛后误差较大；SGD 优化算法与Adadelta 优化算法收敛速度较慢，收敛后误差波动较大；RMSProp 优化算法与Adam 优化算法在收敛速度上较为接近，但Adam优化算法收敛后误差最小，最为平稳，因此选择Adam 优化算法作为模型的优化算法。

模型仿真情况对比：为了验证ReliefF-PCA 降维算法对故障诊断准确率与泛化性，与其他降维算法进行对比验证，各降维算法故障诊断准确率如表2所示。其次，ReliefF-DNN 模型和Pearson-DNN 模型由于对多故障或多风机的泛化能力差，不能有效诊断故障。基于Pearson 相关系数的模型具有良好的降维效果，当只有一个风机齿轮箱油温超标时，相关参数较少。当风机数量增加时，降维效果会变差。

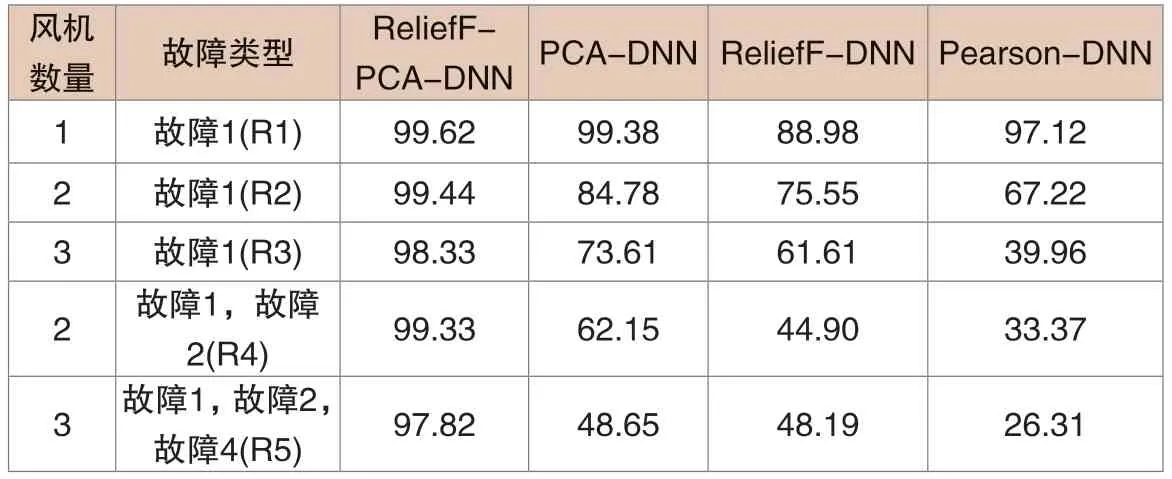
表2 各降维算法故障诊断准确率（%）