基于IPSO-FNN的风电齿轮箱故障诊断方法*
白瑞飞, 张 伟, 赵豆豆
(河南理工大学 电气工程与自动化学院,河南 焦作 454000)
0 引 言
鉴于基于数学建模的故障诊断方法难以满足风电齿轮箱的故障诊断需求[1]。以数据挖掘为方向的故障诊断方法受到研究者的广泛关注。Zhong X Y等人[2]研究了模糊神经网络(fuzzy neural network,FNN),并将其应用于风电齿轮箱的状态监测和故障诊断中。Schlechtingen M等人[3]将状态回归方法和智能神经网络方法应用于风电齿轮箱的故障诊断中,测试两种方法的优劣性,最终智能神经网络方法具有较好的效果。程加堂等人[4]提出一种 CQPSO-BP 神经网络的齿轮箱故障诊断方法,利用混沌序列来初始化粒子的初始角位置,提高种群的遍历性;相比粒子群优化BP(PSO-BP)网络与BP网络的诊断结果,CQPSO-BP算法收敛速度快、识别精度高。李壮等人[5]提出了粒子群优化 KFCM 的齿轮箱故障诊断方法,通过试验验证也取得了很好的效果。但以上粒子群优化(PSO)算法在优化迭代过程中,并没有考虑到粒子的多样性损失问题,因此很有可能会出现早熟收敛现象,影响故障诊断的精度和网络的收敛速度。
本文提出一种基于改进PSO(IPSO)-FNN的风电齿轮箱故障诊断方法,利用数据驱动方法建立系统故障诊断模型。采用PSO神经网络的学习参数,为了提高参数优化性能,引入适应度方差指标判断粒子状态,对早熟的粒子进行差分进化操作,改善粒子群的多样性。同时对惯性权重、学习因子进行改进,以平衡算法的全局搜索和局部开发能力。经风电齿轮箱故障诊断实验研究,本文提出的故障诊断算法具有较好的识别精度和快速的收敛速度。
1 FNN建模
鉴于齿轮箱的振动信号呈现出非平稳性、复杂性、非线性[6]。选取功率谱熵、小波熵、关联维数、盒维数、峭度和偏度作为齿轮箱故障诊断的特征向量,对齿轮正常状态、磨损状态和断齿状态三种状态进行诊断识别。本文采用的网络结构如图1所示。输入层x1~x6分别对应6个故障特征向量,输出的3种状态对应的期望值分别为1,2,3,最终的诊断结果可通过网络输出数值确定。
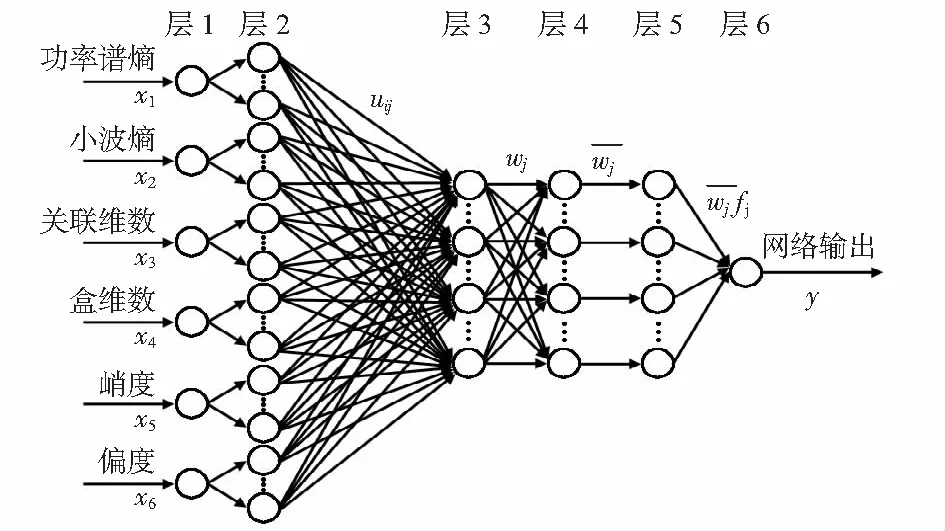
图1 网络结构
第一层为输入层,输入变量为xi,i=1,2,…,n;因单位和量级不同,输入值为归一化后的特征指标参数。
第二层为隶属函数层,将输入信号进行模糊化运算。所选隶属函数
(1)
式中j=1,2,…,m,m为隐含层节点数;cji,bji分别为隶属度函数的中心和宽度。
第三层为模糊规则强度激活层,将模糊化后的各个输入信号进行相乘
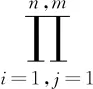
(2)
式中uij为第二层的输出,代表隶属度函数值;wj为第j条规则的可信度。
第四层为规则强度归一化层,计算规则的归一化信赖度
(3)
第五层为计算各个规则的输出
(4)
式中pi,p0为网络的后件参数,fj为后件参数的线性组合。
第六层为计算网络的总输出y为
(5)
2 IPSO算法
2.1 基本粒子群
PSO算法是起源对生物鸟类群体的模仿,在搜索食物过程中通过彼此交流从而快速找到目标,其本质是一种随机搜索算法。假设有m个粒子组成一个群落,其中第i个粒子(i=1,2,3…m)可以用n维向量表示。其中位置表示为xi=(xi1,xi2,…,xin),速度表示为vi=(vi1,vi2,…,vin),个体极值表示为pbest=(pi1,pi2,…,pin),全局极值表示为gbest=(pg1,pg2,…,pgn)。当找到两个最优值时,各个粒子根据如下公式来更新自己的速度和位置
vid=ω*vid+c1r1(pid-xid)+c2r2(pgd-xid)
(6)
xid=xid+vid
(7)
式中ω为惯性权重因子,c1和c2是学习因子,r1和r2为[0,1]区间的随机数。
基本粒子群算法在每次更新迭代中会产生一个最优解,导致出现早熟现象[7]。
2.2 基于DE思想的PSO
为了解决粒子早熟问题,引入差分进化操作,对早熟粒子进行变异、交叉、选择来提高粒子群的多样性,改善算法全局搜索能力。
首先引入粒子群适应度方差σ2来检测算法的当前状态,其表明了粒子的离散程度,可以表示为
(8)
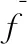
(9)
然后对早熟的粒子进行变异,表示为
ui=x1(k)+f(x2(k)-x3(k))
(10)
式中x1,x2,x3为粒子群中选取的3个不同的个体,F为缩放比例因子。
交叉操作中产生的中间种群di由变异种群ui和父代种群ti共同产生
(11)
式中pc∈[0,1]为交叉概率,rand(0,1)为0~1之间的随机值。最后对中间种群和父代种群进行选择操作。即
(12)
式中xi+1为差分变异操作后的新的粒子种群。
2.3 惯性权重的调整
在PSO中,惯性权重是一个很重要的参数,其数值的设定对算法的全局搜索能力和局部搜索能力有很大的影响[8]。较大的惯性权重可以提高算法的全局搜索能力,而较小的权重有助于算法的局部开发。现有的惯性权重调整策略,大多数为惯性权重的线性递减模式,这种单调的调整方式,在迭代次数达到一定程度时,惯性权重的该变量会很小,导致调节的效果不明显[9]。
本文在惯性权重递减模式的基础上提出一种惯性权重调整方式,其调整范围逐渐內缩并整体上呈递减趋势,有效改善了惯性权重单一变化的模式,有助于增加粒子的随机性与多样性。即
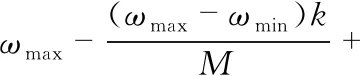
(0.5-r3)((1-k)/M)2
(13)
式中ωmax,ωmin分别为惯性权重的最大值和最小值;M,k为最大迭代次数以及当前迭代次数,r3为(0,1)之间的随机值。
2.4 学习因子的改进
本文采用动态的学习因子调整方式,使c1呈递减趋势,c2呈递增趋势。即算法初期主要依靠粒子自身经验,算法后期依赖粒子群体的信息分享[10]。避免在算法后期出现早熟现象
(14)
式中c1,c2为学习因子;M,k分别为最大迭代次数以及当前迭代次数。
3 仿真验证
3.1 相关参数设置及实验数据
本文以某风电场 1.5 MW 风机组为研究对象,提取齿轮箱的振动加速度信号,采样频率为 4 400 Hz,每个样本采样点数为7 350点。针对本文的研究问题,参数设置及实验数据的选取如下:粒子群规模30,迭代次数150,ωmin=0.4,ωmax=0.9,c1,c2∈(0.2),F=0.5,pc=0.3,适应度函数为网络输出与目标向量的差值;模糊神经网络采取6—13—1结构,学习因子以及动量因子分别设置为0.10,0.04, 训练次数为120次。另外选取各种类型故障数据15组,由于各单位数据量级不同,需要对其归一化处理,构成FNN的训练样本,导入到网络结构。其部分训练样本如表1所示。
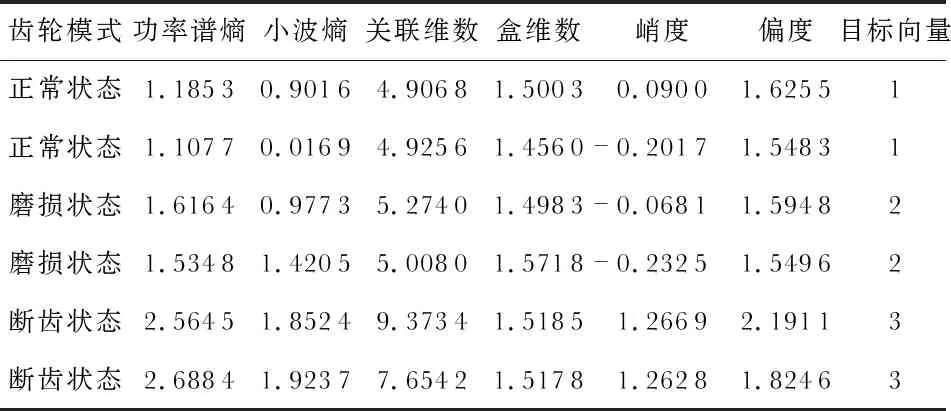
表1 部分训练样本
3.2 基于IPSO算法的诊断模型研究
本文首先利用改进粒子群对模糊神经网络的中心、宽度以及后件参数进行优化。具体优化流程如图2所示。
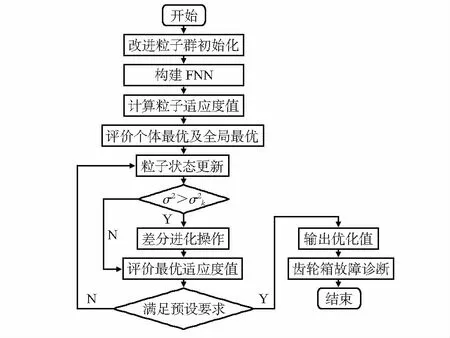
图2 改进粒子群优化流程
将经IPSO后的隶属函数中心、宽度以及后件参数作为初始值导入到模糊神经网络进行训练,部分训练样本同表2一致。训练次数为150次,其余参数同上所述。同时与PSO的FNN以及未被优化的FNN进行对比。结果如图3所示。
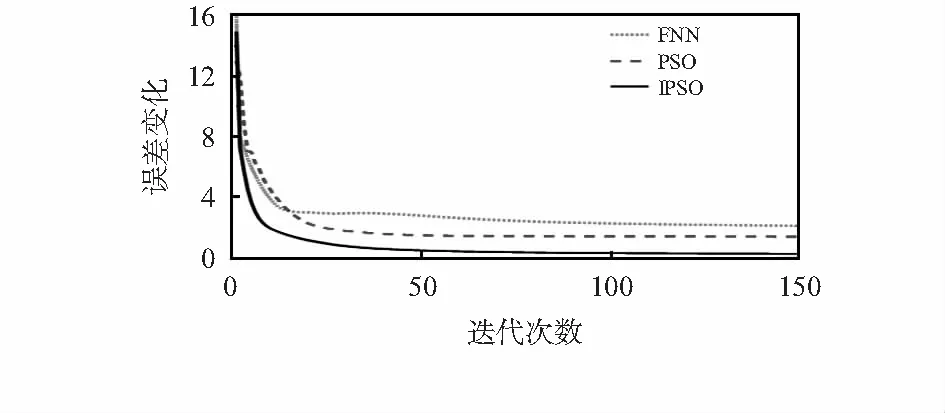
图3 误差对比
从图中可以看出,本文采用的IPSO算法在50次迭代之前就已下降到较低误差水平并逐步趋近于收敛,而其余两种算法无论在收敛精度还是速度方面都没有IPSO算法的可靠性高。
为了更直观地说明本文采用的IPSO算法的有效性,将测试样本输入到训练好的网络中,测试样本如表2所示。结果对比如表3所示。
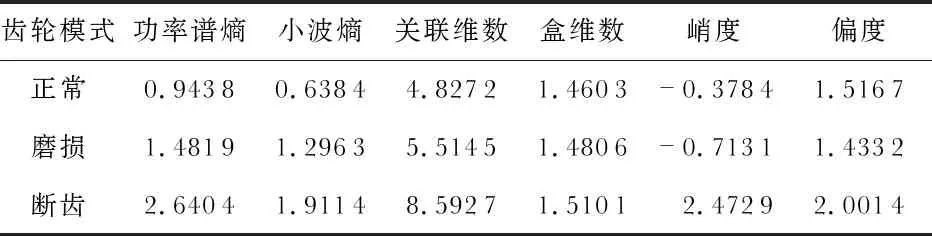
表2 部分测试样本
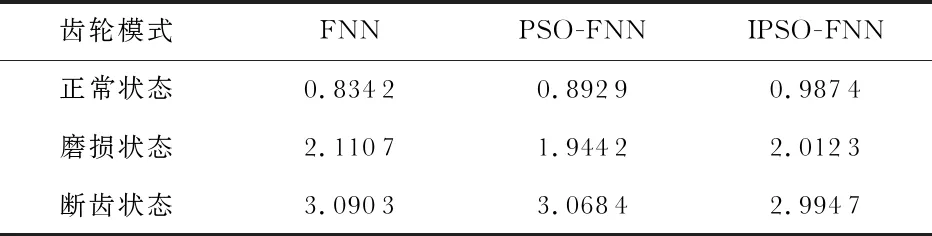
表3 诊断识别结果
齿轮断齿状态下,从表中可以直观地看出,FNN和PSO-FNN的输出数值分别为3.0903,3.0684,而IPSO-FNN算法精度却可以达到2.9947。另外经计算,IPSO算法诊断结果的平均绝对误差仅为1 %,但PSO算法以及FNN算法则分别为7 %和12 %。因此本文提出的IPSO-FNN 相较于 FNN 和 PSO-FNN 算法有收敛速度快、诊断精度高等优点,更符合诊断要求。
4 结 论
通过对惯性权重以及学习因子的调整,改善算法的空间搜索能力,同时为了提高粒子群的多样性,避免局部收敛,引入了差分进化方法对早熟的粒子进行操作。极大地改善了算法的寻优能力及优化效率。将本文采用的优化方法同FNN结合对风电齿轮箱进行故障诊断,与PSO-FNN算法和FNN算法相对比,本文提出的方法有较高的收敛速度和精度。可以更有效的应用于风电齿轮箱故障诊断。

