基于优化一致性算法的微网功率经济分配策略*

朱乔红， 龙英文， 余 粟

(1.上海工程技术大学 电子电气工程学院,上海 201620；2.上海工程技术大学 工程实训中心,上海 201620)

0 引 言

微电网是由分布式发电、储能装置及负荷等构成的局域网系统，具有孤立和并网两种运行模式，未来通过微网对分布式电源的运行管理将成为智能配电网发展的目标之一[1～4]。

经济调度是电力系统发电调度中的基本问题之一，其本质上是一个优化问题，目标是在满足总需求和满足单个发电机输出限制的同时最小化总发电成本[5,6]。传统采用集中式优化的经济调度方法，例如粒子群算法[7]、细菌觅食算法[8]等。在采用集中式优化的方法时，通过调度中心采集整个系统的调度对象信息，再进行优化计算，最后将指令发送至各个调度对象。这种集中式控制框架可能受到性能限制，例如通信要求和成本高、故障率高、计算负担大、灵活性和可伸缩性有限。

各种分布式算法已经被开发用于共识、交会、形成和优化。因此，研究人员开始将这些分布式算法或其变型应用于电力系统问题。例如文献[9]提出了一种分布式架构，用于带有同步发电机和逆变器接口电源的孤岛交流微电网的发电控制。

本文简单介绍了一致性算法的基本概念，由于被控单元之间距离远，存在通信滞后，可能影响系统性能，因此在一致性算法的基础上进行了改进，有效地克服通信滞后，使系统具有很好的收敛性能。在传统下垂控制的基础上增加了成本最小化控制器，实现成本最小化下的功率分配。

1 一致性算法改进

1.1 传统一致性算法

令xi代表节点i的状态变量，ui代表节点i的输入状态，通常各节点只与其邻居节点相互通信，用一阶离散系统表示节点状态

xi(k+1)=xi(k)+ui(k),i=1,2,…，n

(1)

节点与邻居节点可获取对方的状态，构造输入为

(2)

式中aij为节点连接图的邻接矩阵中的元素。

根据式(1)和式(2)，矩阵形式和平均值如下

x(k+1)=Dx(k)

(3)

式中x(k)为各节点第k次迭代的值，D为系统的状态转移矩阵，且满足矩阵行向量或列向量元素之和为1；若状态转移矩阵D构造为双随机对称矩阵，则系统一致收敛于平均值。

目前已有文献提出的多种分布式分层控制方法大多都假设通信网络是完美的，可忽略通信延时[10,11]。但在实际应用中，通信网络中经常会出现通信延时，有可能会限制一致性算法的收敛性，使得整个系统性能变差。文献[12]研究了在通信延时和数据丢失后的多智能体系统的稳定性和一致性；文献[13]研究了在通信延时下基于一致性的经济调度算法。

1.2 改进一致性算法

令Y(k),ΔY(k),X(k-τ),Y(k-τ)为与X(k)相对应的N维列向量。Y(k)为节点第k次迭代的值，即有

Y(k)=AX(k)+BΔX(k)

Y(k)-Y(k-τ)=A[X(k)-X(k-τ)]+

B[ΔX(k)-ΔX(k-τ)]

(4)

式中τ为延时量，A,B为系数矩阵,ΔX(k)为作用误差。

如果迭代频率较快的话，一致性算法就能够快速收敛，那么ΔX(k)=ΔX(k-τ)，即式(4)改为

Y(k)-Y(k-τ)=A[X(k)-X(k-τ)]

(5)

若达到收敛状态，则有X(k)=X(k-τ)，即根据式(5)得Y(k)-Y(k-τ)=0,与此同时，如果系统拓扑结构受影响改变，系统已经到达稳态，则系统状态不会变化。若未迭代敛收，则系统状态处于一直改变状态。根据系统状态情况不稳定，构造动态一致性算法如下

X(k+1)=Y(k)-Y(k-τ)+DX(k)

(6)

2 微网功率经济分配策略

2.1 一次控制器

如图1所示，在一次控制层中，电压和频率的下垂方程式为

E*=E0-mQ*

ω*=ω0-n(P*-Pref)

(7)

式中E*和ω*分别为参考电压幅值和参考角频率；E0和ω0分别为额定电压幅值和额定角频率；m和n分别为无功下垂系数和有功下垂系数；Q*和P*分别为实际无功功率和实际有功功率；Pref为成本最小化控制器的参考功率。

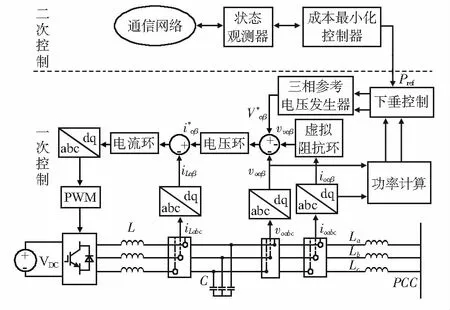
图1 成本最小化功率分配控制结构

2.2 二次控制器

在二次控制层中，成本最小化控制器用于解决功率分配下的成本最小化问题，将参考功率Pref传输到一次控制器中，利用拉格朗日乘子法求解， 代表与等式约束对应的拉格朗日乘子，为将算法分布化，利用对偶分解先算出初步分布式系统优化迭代方程为[14]

λk+1=λk+μΔPk

(8)

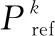
本文采用频率下垂控制器的特性来收集整个系统功率信息，假设微网中有N个节点均由下垂控制器控制，且下垂系数均为n,则根据式(7)得到

(9)

式中Pti为实际输出有功功率，ωti为实际输出频率。

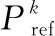
(10)

式中ε为收敛系数，aij为描述节点间的连接状态，若节点i与节点j之间有通信，则aij=1；反之则aij=0。根据式(9)和式(10),更新拉格朗日乘子方程为

(11)

3 仿真验证

为了验证本文提出算法的有效性，采用如图2所示的380 V/50 Hz,IEEE 9节点微网系统进行仿真运行。微网系统中6个分布式电源，其中节点DG1-DG6代表发电机，DG7代表光伏电源。DG7输出功率为15 kW，系统中的有功负荷为160 kW，储能系统的输出功率为20 kW，假设6台发电机的经济参数如表1所示。根据成本最小化控制器需要，采用DG1-DG6的组成通信网络，如图2所示。

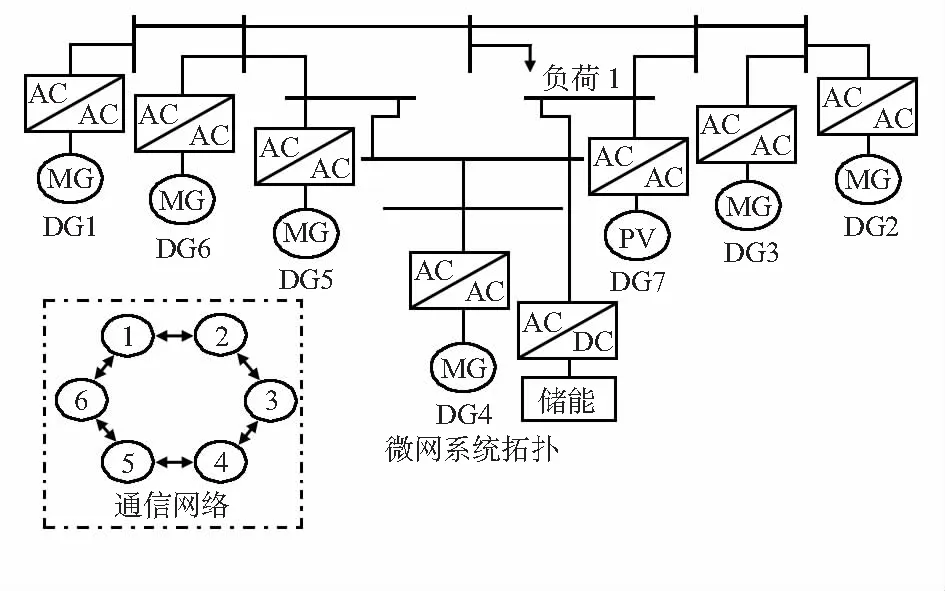
图2 微网拓扑结构

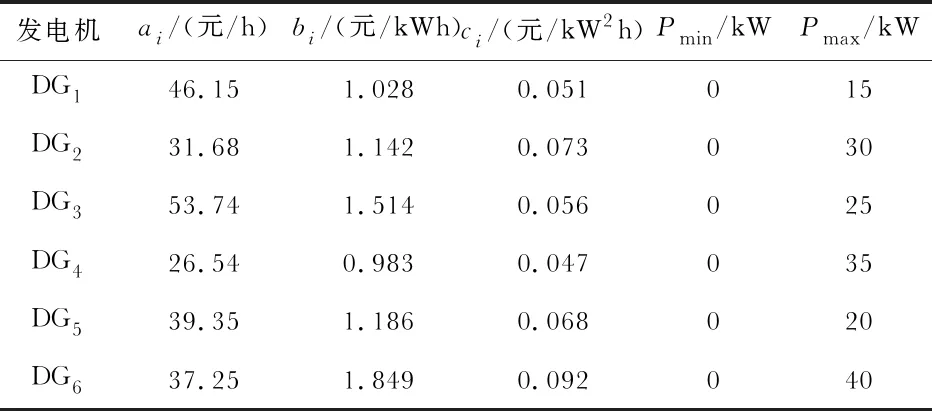
表1 发电机系统的参数

集中式调度时，采用λ迭代法，可求出次微网系统经济调度最优解λopt=3.6012。且各节点功率最优解分别为:P1=25.2 kW，P2=16.8 kW，P3=18.6 kW，P4=27.8 kW，P5=17.7 kW，P6=9.5 kW。

3.1 延时对系统的影响

为了分析网络延时对系统的影响，在MATLAB仿真平台上完成了延时时间τ=0.001 s的系统运行测试，设定成本最小化控制器迭代更新间隔为0.001 s，初始拉格朗日乘子分别为:λ1=1.4，λ2=2.6，λ3=3.5，λ4=3.8，λ5=2，λ6=4.1，收敛系数ε=1/5，常数μ=1/5。在0～0.001 s，成本最小化控制器未启动。设定参考功率初始值分别为P1=3.65 kW，P2=9.98 kW，P3=17.73 kW，P4=29.96 kW，P5=5.99 kW，P6=12.23 kW。由于下垂控制，输出频率小于额定值50 Hz。

测试0.001 s后，成本最小化控制器启动，仿真结果如图3(a)，根据实际功率和参考功率的差值，每0.001 s更改各节点拉格朗日乘子，拉格朗日乘子一致性迭代过程呈振荡形式收敛，最终收敛到最优值3.60，收敛迭代次数大约23次，收敛时间T=23×0.001=0.023 s。从图3(b)可知，各节点的参考功率和输出功率在0.023 s后都达到最优值。

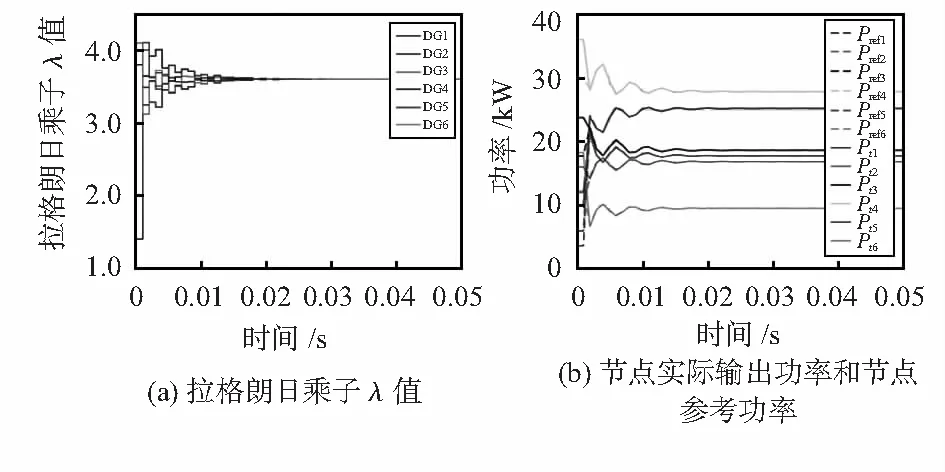
图3 通信延时

3.2 改进算法性能测试验证

为了验证本文改进算法能否收敛到最优解，测试0.001 s后，成本最小化控制器启动运行，实验结果如图4所示，从图4(a)中可以看出拉格朗日乘子收敛比较平缓，最终也收敛到最优值3.60，收敛迭代次数大约13次，收敛时间T=13×0.001=0.013 s。从图4(b)可知，各节点输出功率和参考功率都在0.013 s后收敛到最优值。

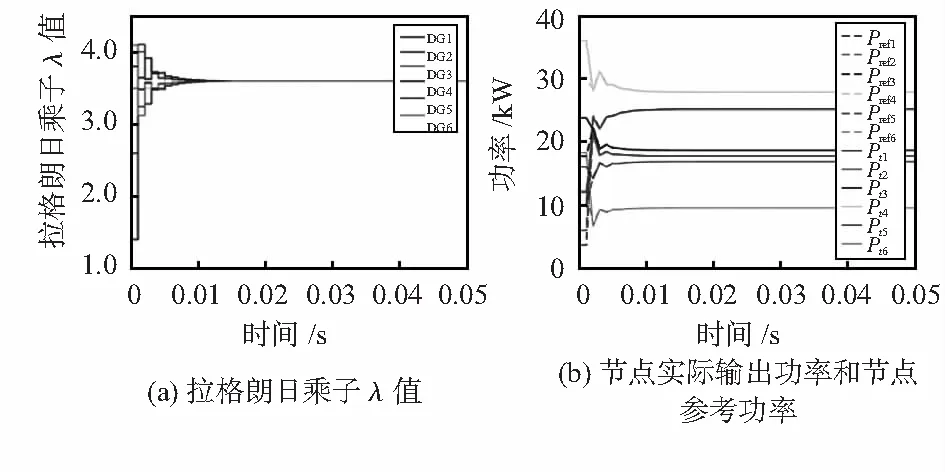
图4 改进一致性算法

4 结 论

本文提出了一种基于优化一致性算法的微网功率经济分配策略。通过在一致性算法的基础上进行了研究并改进，有效地克服通信滞后，使得系统具有很好的收敛性能。根据一致性算法和下垂控制信息设计了成本最小化控制器，实时控制微网各电源出力，使得成本最小化下实现微网功率分配。