非封闭式FDM 3D打印机喷头温度控制器研究*
张金立, 施一萍, 刘 瑾, 吕晨悦, 程宗政
(上海工程技术大学 电子电气工程学院,上海 201600)
0 引 言
熔融沉积成型(fused deposition modeling,FDM)技术[1]是3D打印成型技术中的一种,而热熔喷头的温度控制是影响FDM技术成型精度最重要的因素。由于非封闭式FDM 3D打印机的打印环境与外界环境没有隔离,影响温度的因素更加复杂,因此对其喷头温度自适应控制显得非常重要[2]。
由于反向传播(back propagation,BP)神经网络良好的逼近非线性系统的能力,与传统比例—积分—微分(PID)相结合所设计的控制器在工业控制中得到广泛应用[3,4]。BP神经网络由于依赖于网络的初始权值和阈值,在训练时收敛速度慢且易陷入局部极小。杨玉东等人采用粒子群优化(PSO)BP神经网络,但是存在过早收敛的问题[5]。陈闯等人采用遗传算法(genetic algorithm,GA)优化神经网络,但是遗传算法收敛速度过慢[6]。
本文提出一种收敛速度快、全局寻优能力强的改进鲸鱼优化算法(improved whale optimization algorithm,IWOA)对BP神经网络初始权值和阈值进行优化,并设计一种IWOA-BP-PID喷头温度控制器。
1 喷头温度控制器
1.1 鲸鱼优化算法
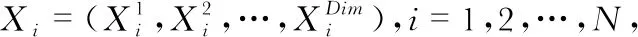
1)包围
假设初始化群体中适应度最高的鲸鱼个体为潜在猎物,群体中的其他鲸鱼向潜在猎物移动,移动时更新位置如下
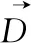
(1)
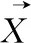

(2)
a=2-2t/Tmax
(3)
式中rand为[0,1]之间的随机数,a为随着迭代次数的增加从2线性递减到0的收敛因子。具体表示如式(3)所示,Tmax为最大迭代次数。
2)猎杀
模拟鲸鱼群捕食过程中猎杀猎物的行为如下
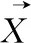
(4)
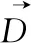
3)搜寻
当式(2)中A的绝对值大于等于1时,这时便不能以迭代过程中产生的潜在猎物为目标对象更新位置,而是随机的将参与本次围猎的鲸鱼群中的鲸鱼作为潜在猎物,算法以这种方式来增强其全局搜索能力。数学模型如下
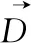
(5)
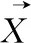
(6)
传统的WOA设计鲸鱼群以式(4)猎杀猎物时,还需要以式(1)来包围猎物,为了使鲸鱼群执行这两个捕食行为,设计用随机数p来实现,具体数学模型如下
(7)
1.2 IWOA
本文针对WOA易陷入局部最优发生早熟而及早收敛的问题,提出一种改进的全局寻优能力较强的WOA。
传统的WOA中当随机概率p≥0.5时,算法直接执行猎杀步骤,这样也会陷入局部最优,因此本文设计当要执行猎杀步骤时先进行前一次迭代个体的适应度与本次个体的适应度进行比较。如果前一次迭代个体的适应度大于本次迭代的适应度将可以认为已找到最优猎物,直接进行猎杀;反之再进行此时A的绝对值与1的比较,这样设计进一步增多算法的包围与搜索环节,使算法的全局搜索能力进一步增强。自适应猎杀改进的执行逻辑如下:
Ifp≥0.5 and fitness(t-1)>fintess(t) ,猎杀
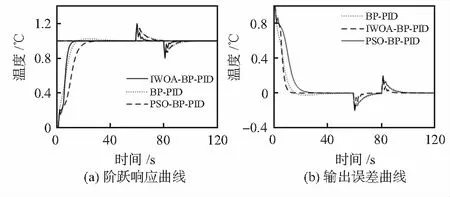
Ifp≥0.5 and fitness(t-1) If |A|<1,包围 If |A|>1, 搜索 IWOA优化BP(IWOA-BP)神经网络核心思想为: 通过鲸鱼群的迭代代替BP算法输出误差的梯度修正。将BP神经网络的连接权值和阈值映射为鲸鱼个体的位置向量,向量的维数根据权值和阈值的个数确定,通过鲸鱼群的寻优机制,获取到使得网络误差达到最优的网络初始权值和阈值。 图1中温度控制器由IWOA-BP神经网络和常规PID控制器构成。BP神经网络通过输入rin和输出yout及误差e对PID的三个参数KP,KI,KD在线自适应调整,得到PID控制器的输出u作为喷头对象数学模型的输入,最后得到整个控制系统的输出yout。系统运行时,神经网络的初始权值和阈值由IWOA优化获取,IWOA-BP神经网络对PID控制器的控制参数自动调节,得到最优控制参数KP,KI,KD使得对喷头温度的控制效果最佳。整个算法运行过程如图2所示。 图1 IWOA-BP-PID控制器 图2 算法运行流程框图 为了测试IWOA的有效性,本文选取可变维单模态函数f1,f2测试改进算法的收敛速度,选取可变维多模态函数f3,f4测试改进算法的全局寻优能力[9]。所选基准测试函数如表1所示。 表1 基准测试函数表 本文选择对比WOA,GA,PSO与IWOA的性能,基准函数维度为30,各算法迭代次数最大1 500。由于算法中有随机量的影响,因此实验的数据均以算法独立运行20次的最优为标准。结果如表2所示,无论是多模态函数还是单模态函数,IWOA在全局寻优效果和收敛速度上最好,PSO次之,GA最差。 表2 WOA与IWOA性能测试表 使用MATLAB软件,对传统BP-PID使用WOA,IWOA,GA,PSO算法进行优化,对喷头对象数学模型G(s)=0.233e-17.5s/(26.3s+1)进行仿真。神经网络取η=0.35,惯性系数α=0.015,初始权值的取值范围[-1.5,1.5],各算法初始化群体为30,迭代次数100,各算法获取到最优权值和阈值时的迭代次数如图3所示,IWOA迭代次数最少,PSO次之。运算时间IWOA为4.3 s最少,PSO 5.4 s次之,WOA为10.24 s,GA为47.6 s最多。所得结果与基准测试函数相同。 图3 各算法优化BP迭代次数 图4为IWOA,PSO优化的PID参数与未优化时PID参数变化对比图。由于WOA与GA相对较差不用再做比较。 图4 三种算法对应PID参数 由图4可知温度控制器在调节温度至稳定的开始阶段都会存在误差而震荡,并且持续时间较长,图4(c)中未被优化的BP-PID控制器表现最明显。相比于PSO,IWOA的优化效果如图4(a)所示,PID参数没有超调,且能快速的稳定。 IWOA-BP-PID,PSO-BP-PID及传统的BP-PID单位阶跃响应曲线如图5(a)所示,对应误差曲线如图5(b)所示。如图5(a)所示,由于在算法运行前期,PSO与IWOA都在寻找最优的权值和阈值,因此与BP-PID的控制曲线重合,但当最优的权值和阈值赋值给BP神经网络之后,IWOA-BP-PID便快速的上升至稳定。三种控制器达到稳定的时间分别约为16,26,43 s,并且传统的BP-PID还有少许的超调。在60~80 s之间加20 %方波噪声,PSO-BP-PID与传统的BP-PID的都不能快速的稳定,IWOA-BP-PID表现出了较强的抗干扰性,至稳定所需时间10 s,且误差最小,能够改善非封闭式FDM3D打印机在模型打印过程中由于温度受干扰而出现的模型表明粗糙、打印过程出现断丝等情况。PSO-BP-PID与传统的BP-PID所需时间分别为18,20 s,时间相对较长,且误差相对较大。 仿真表明:基于IWOA-BP-PID的喷头温度控制器调节温度至稳定快,无超调,自适应能力强,对非封闭式FDM 3D 图5 三种算法的阶跃响应曲线和输出误差曲线 打印机有较高的使用价值,对影响情况复杂的且用硬件来改进温度控制的3D打印机也有较高使用价值。由于软件的可移植性较好,该温度控制器也可以用作其他设备的温度控制。1.3 IWOA优化BP神经网络原理
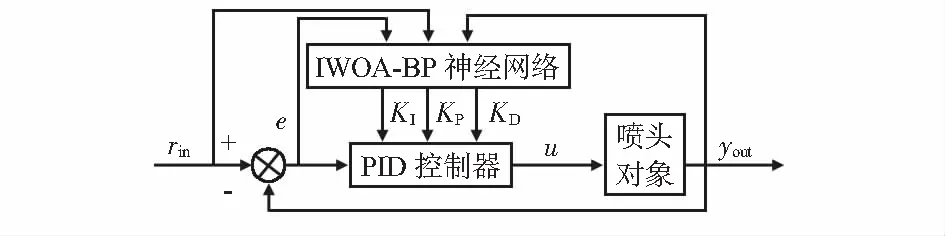
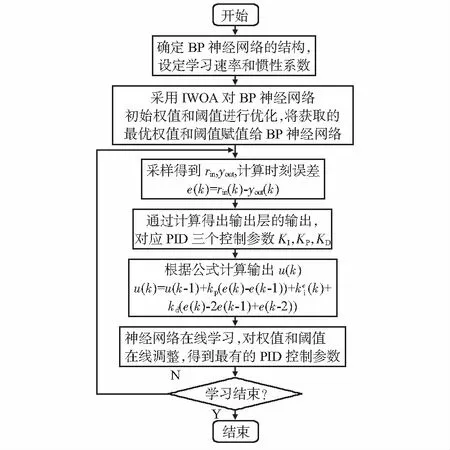
1.4 IWOA-BP-PID喷头温度控制器
2 仿真实验
2.1 IWOA性能测试

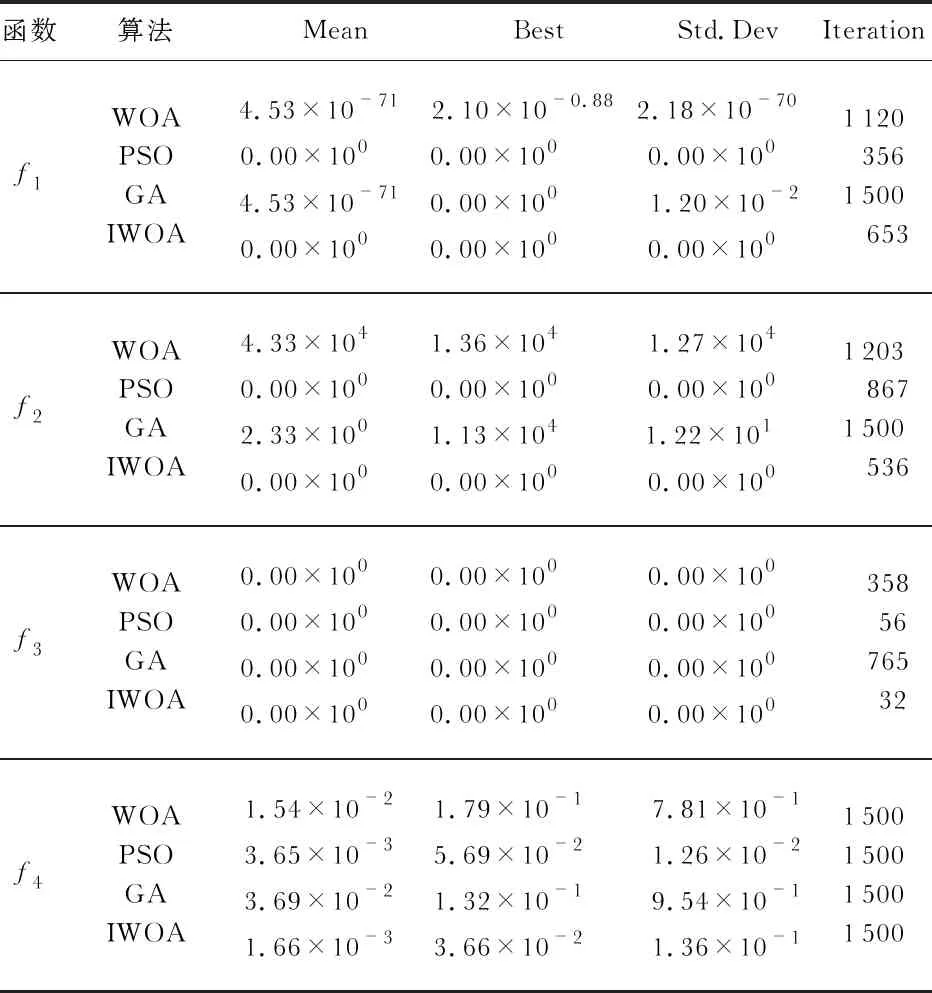
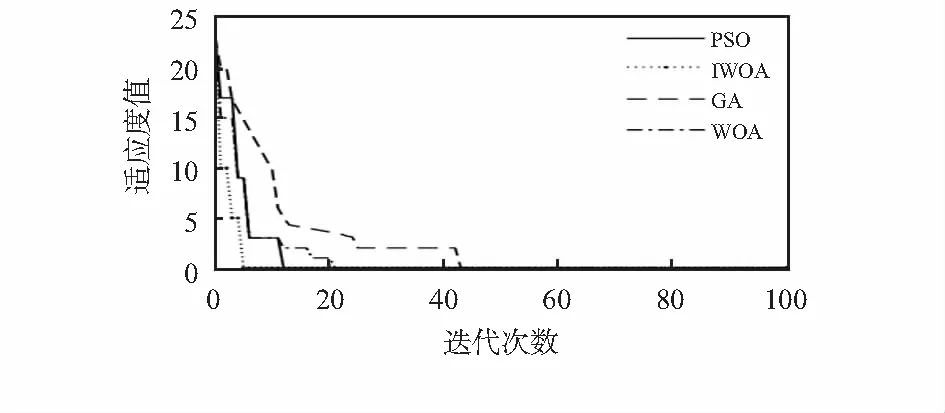
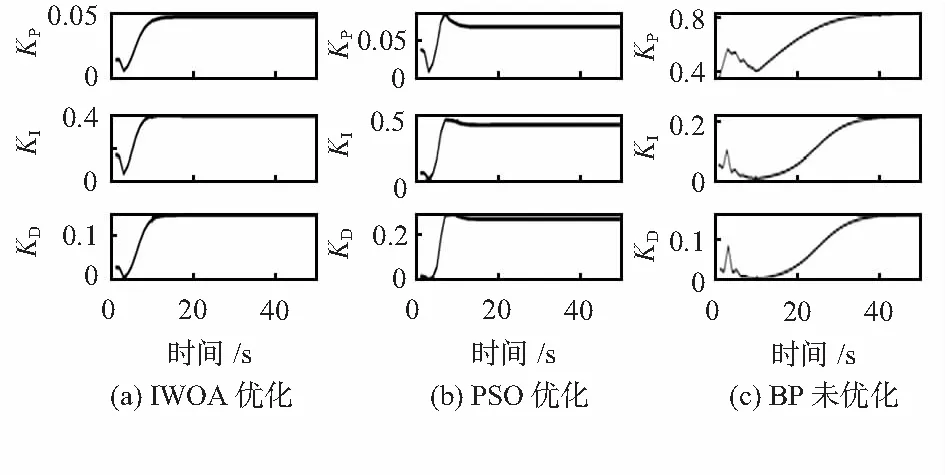
2.2 MATLAB仿真实验
3 结 论