基于改进PSO算法的光伏发电系统MPPT控制策略*

孙 恺， 刘光宇

(杭州电子科技大学 自动化学院，浙江 杭州 310000)

0 引 言

太阳能在光伏(photovoltaic,PV)发电领域运用越来越广泛，由于光伏电池独特的非线性I-V特性，光伏电池功率输出受环境的影响很大，为了保证光伏发电系统能够工作在最大功率点下以提高光伏发电系统的效率达到充分利用太阳能，研究人员在光伏发电系统中引入了最大功率点跟踪(maximum power point tracking,MPPT)技术。其中有传统的控制方法如电导增量(incremental conductance,INC)法[1,2]，扰动观察(perturb and observe,P&O)法[3]等和智能控制算法如光伏发电系统如遗传算法(genetic algorithm,GA)[4]、人工神经网络(artificial neural networks,ANN)[5]、蚁群优化(ant colony optimization,ACO)算法[6]、粒子群优化(particle swarm optimization,PSO)算法[7～9]等。传统的方法在均匀光照条件下的跟踪具有良好的效果，在局部遮挡情况下传统控制方法常常会陷入局部最大点,但智能算法表现出良好的性能。其中PSO算法被广泛应用于各个领域[10～12]在MPPT控制中应用的最为广泛。传统的PSO算法虽然能够跟踪到全局最大功率点但仍然存在搜索时间长，收敛精度差，不够稳定,剧烈振荡等问题[13]。

本文提出采用非线性的加速因子和学习因子并采用动态的惯性权重来提高PSO算法的搜索时间和收敛精度，搜索振荡。

1 光伏阵列特性

如图1所示是典型的4个光伏模块串联而成的光伏阵列模型。在光伏发电系统中，太阳的光照强度对光伏阵列产生的输出功率具有很大的影响，当光伏阵列接收到的太阳光照强度越强时，输出的电流就越高从而输出功率也越高；反之输出电流和输出功率也越弱。当整个PV阵列所受到的太阳辐射是均匀的，如图1(a)所示，光伏阵列的P-V曲线只存在唯一的极值点即全局最大功率点(maximum power point,MPP)。当出现部分阴影的情况时光伏阵列受到的光照强度不同，如图1(b)所示第1块、第2块以及第3块光伏模块存在不同程度阴影遮挡导致两个模块之间的日照差异从而激活了模块1,2,3的旁路二极管。因此，在I-V曲线存在四个阶梯电流波形，相应的P-V特性曲线出现了3个局部峰值和1个全局峰值。

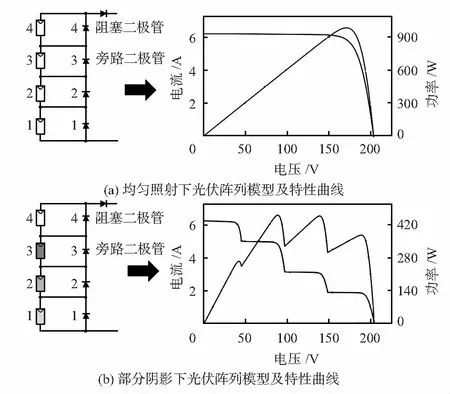
图1 光伏阵列模型及特性曲线

2 基于PSO的MPPT控制策略

2.1 光伏发电系统MPPT控制框架

光伏发电系统MPPT控制框图如图2所示。图2中光伏阵列有两个输入E和T，分别是模块上分布的辐照度和温度。采用MPPT控制策略改变DC-DC变换器的占空比D(t)，以调节终端电压Vref(t)，使得输出功率Pout向MPP方向转移。

图2 光伏发电系统MPPT控制框图

2.2 PSO算法的MPPT控制策略

PSO算法是一种启发式算法，用于寻找D维空间中优化问题的最佳解。 群体中个体的信息共享使得整个群体的动作遵循问题解决空间中的最优个体，从而获得最优解。 群体中的每个粒子遵循两个基本规则来找到最佳解决方案，其遵循最佳性能粒子和粒子本身找到的最佳解决方案[14]。由于在光伏发电系统MPPT极值搜索问题中解空间是一维的，因此可以将公式简化为

(1)

式中w为惯性权重保持粒子的运动惯性，当w值较大时，算法的全局收敛能力较强，但局部搜索能力较弱，反之，则局部搜索能力较强，全部搜索能力较弱。c1和c2学习因子，当选择的值c1太小时，粒子群会更快地收敛，但它将落入局部最优解；当c2选择太小时，则粒子群中各个粒子之间相互影响将减小，最终将相当于多个粒子进行独立搜索，很难得到最优解。r1和r2为[0 1]之间的随机数，Pi为第i个粒子自身的最佳位置，所有粒子的最佳位置都表示为Pg。在基于PSO算法的光伏发电系统MPPT控制中，通常用PSO算法中的每个粒子位置xi来表示DC-DC转换电路的占空比D，并且 PSO算法使用等式(1)来持续不断更新粒子的位置来从而来不断的更新DC-DC电路的占空比D直至收敛到光伏发电系统的最大功率点。

2.3 改进PSO算法的MPPT控制策略

传统引入的线性递减的惯性权重在迭代初期局部搜索能力较弱，容易错过全局最优点，而在迭代后期全局搜索能力变弱，容易陷入局部极值。本文使用如式(2)的动态惯性权重来避免这一问题

ω=ωmin+rand/2

(2)

在算法搜索的初期看重粒子自身的搜索能力，算法搜索的后期则应注重全局最优粒子。因此本文对学习因子c1采用了非线性递减的余弦函数，学习因子c2采用的是非线性递增的反正切函数

(3)

选择这样的自适应参数能够加快算法的收敛速度同时能够提升算法跟踪的准确性，改进算法流程图如图3所示。

图3 改进PSO算法的MPPT控制策略流程图

3 实验验证分析

本文采用MATLAB/SIMULINK搭建了4个光伏电池单元组成的串联阵列模型的具有MPPT控制的光伏发电仿真系统。实验参数仿真时间为0.4 s，系统采样时间0.001 25 s，PWM频率为0.000 01 s,环境温度25 ℃,4个光伏电池的光照强度(1000，750，500，250)W/m2，最大输出功率295 W。在搭建同一仿真实验环境下对传统PSO算法、线性自适应参数的PSO(linear PSO,LPSO)算法、非线性自适应参数的PSO(nonlinear PSO,NPSO)算法进行仿真实验，实验中算法参数设置如表1所示。

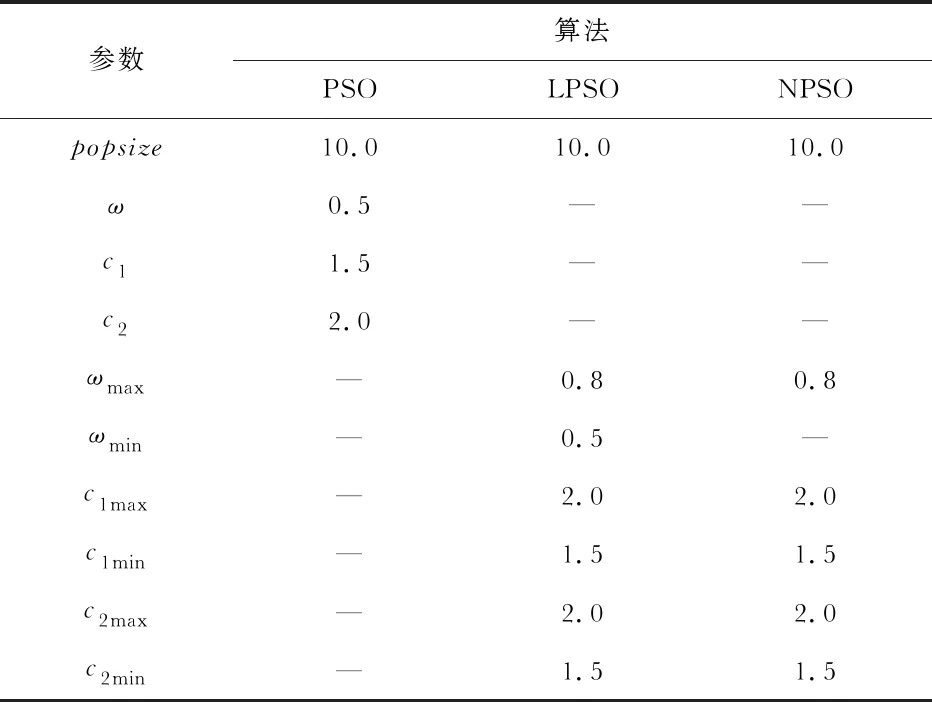
表1 算法参数设置

三种PSO算法在光伏发电系统的MPPT控制中的仿真实验结果，如图4所示。

图4 三种PSO算法的性能分析图

从图4(a)可以看出:PSO算法虽然能够解决在出现局部阴影时光伏发电系统的最大功率点跟踪问题，但收敛时间过长同时搜索振荡剧烈，稳定性较差。如图4(b)所示LPSO算法在一定程度上提升了PSO算法的收敛时间和搜索振荡以及稳定性问题，但在算法搜索初期的振荡还是剧烈。图4(c)是NPSO算法的性能分析图，从图中可以看出:NPSO算法的收敛时间较短且稳定性较好同时与前两种算法相比较对搜索振荡进行了优化。采用稳态误差e表示算法的跟踪准确性

(4)

稳态振荡δ表示为

(5)

仿真实验结果性能分析如表2所示。

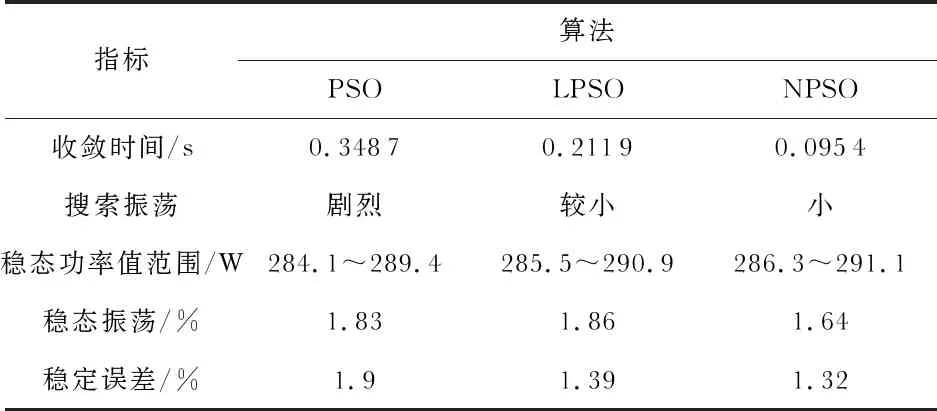
表2 三种算法仿真实验结果性能分析

为了验证本文提出的非线性自适应参数的粒子群算法的实际可行性，搭建了光伏发电系统的最大功率跟踪实验平台。该实验平台由遮挡过最大功率为16W的光伏电池板、MPPT控制DC-DC电路、功率检测器、遮挡物和负载。 在搭建的实验平台进行了三种算法的控制策略的实验，实验跟踪结果图如图5所示。

图5 三种策略真实实验跟踪结果

图5(a)是PSO算法的跟踪结果图，在真实的实验平台中进行实验可以看出:PSO算法的控制策略的搜索时间过长，同时振荡剧烈，稳定性较差。图5(b)是LPSO算法的跟踪结果图。与PSO算法相比较，LPSO算法的跟踪效果有了一定的提高，在收敛时间上得到了提升，同时振荡减小，稳定性提升。图5(c)是NPSO算法的跟踪效果图，可以看出NPSO算法与LPSO算法相比较，在收敛时间和振荡上又有了较大提升。

三种控制策略的实验结果性能分析在表3中给出。

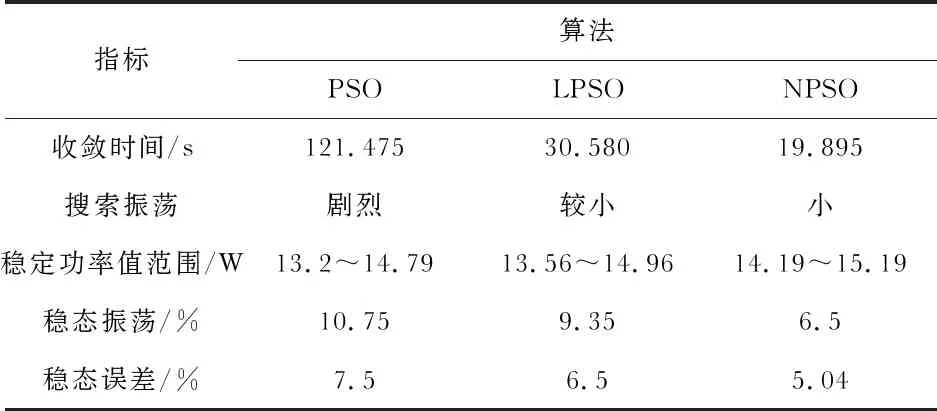
表3 三种算法的工程实验结果

4 结 论

基于仿真实验和工程实验的结果，本文提出的NPSO算法即使在局部阴影条件下也具有良好的跟踪性能,无论在收敛时间、搜索振荡、效率以及稳定性NPSO算法都优于其他两种控制策略。说明在同一环境下,本文提出的控制策略能够保证快速准确跟踪到光伏发电系统的最大功率点的同时减少搜索振荡。