基于小波分解和 Hilbert 包络谱分析的电池故障诊断方法

常春，王启悦, 姜久春*，高洋，吴铁洲

（1. 湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室，湖北 武汉 430068；2. 欣旺达电子股份公司，广东 深圳 518108；3. 华南理工大学电力学院，广东 广州 510641）

0 引言

动力电池作为电动汽车的主要动力来源，当电池出现一些明显或不易检测的故障时，容易引起电动汽车以及人身安全问题[1]。由于单体电池不能满足电动汽车的动力需求，单体电池通常以串并联成组的方式存在。如果其中一只单体电池出现故障，就会对整个电池组有重大的影响，因此对电池故障进行提前预警具有十分重要的意义[2]。常用的电池故障诊断方法主要有基于电池模型的和基于数据驱动的两类。由于电池原理复杂，建立的电池模型适应性小。相对来说，数据驱动方法无需分析电池内部机理，所以灵活性较强。数据驱动方法是对系统的运行数据进行信号分析和处理，提取反映电池故障的特征参数，结合相应算法进行电池故障的检测和识别。Xia 等人使用移动窗口过滤器对采集的电压数据进行处理，提取历史时间窗口内电压数据的相关系数作为故障特征，并基于数据驱动的故障诊断方法，通过相关系数下降与电池异常电压降的关联关系，在线识别电池短路故障[3]。Yang 等人针对外短路实验中发生的电解液泄漏行为，使用随机森林的分类方法，以电池容量和温升作为故障表征参数来判断故障信息。并计算实测电压与估计电压之间的均方根误差，通过设置不同大小的阈值，对电解液泄露的情况进行预警[4]。Yao 等人采用离散小波变换的信号特征提取方法，对电压数据进行降噪处理，提取电压数据的电压差、协方差和方差作为故障特征，并且基于数据驱动的故障诊断方法，按照电压故障曲线波动的严重程度，将故障分为 4 个等级后，利用提取的故障特征对广义回归神经网络进行训练，然后根据神经网络的输出结果，实现了对锂电池内部连接松动的故障检测，以及对不同故障程度的预警[5]。Chen 等人通过分析充电过程中的部分容量增量曲线提取了 6 个故障特征，用一种名叫弹性网的收缩方法进行降维处理，得到与容量衰减最相关的 2 个故障特征——最小容量增量值和曲线峰值，然后利用这些故障特征训练高斯分类器，识别容量不足的故障电池[6]。Muddappa 等人提取锂电池的电压、温度和电荷状态作为故障特征，基于模糊逻辑的知识故障诊断方法，将故障特征与电池工厂模型的相关数据进行比较，生成残差信号，然后通过设置残差信号的隶属度函数及范围检测电池的老化故障[7]。Sun 等人使用小波变换的方法，得到去噪电压数据，提取电压数据的香农熵作为特征参数，然后通过设置阈值检测电池的故障[8]。上述方法主要通用信号处理进行特征提取，而且提取的特征主要是电池电压的相关系数、方差等时域参数，因此较难检测没有明显征兆的异常信息，而且无法实现提前预警。

针对以上问题，笔者先利用小波分解提取明显反映电池故障信息的高频细节信号，接着采用希尔伯特变换（Hilbert Transform）提取频域中包络谱特征参数，然后利用离群点检测算法实现电池故障诊断和提前预警，并通过实验验证该方法的有效性。

1 故障诊断方法介绍

针对电池故障信息表现不明显状态，利用小波分解将电压信号分解为低频近似信号和高频细节信号。其中，高频细节信号可以明显反应故障信息。之后，利用希尔伯特变换求解细节信号包络谱，并提取包络谱平均值作为离群点检测特征值，实现故障诊断。具体的电池诊断流程如图1 所示。

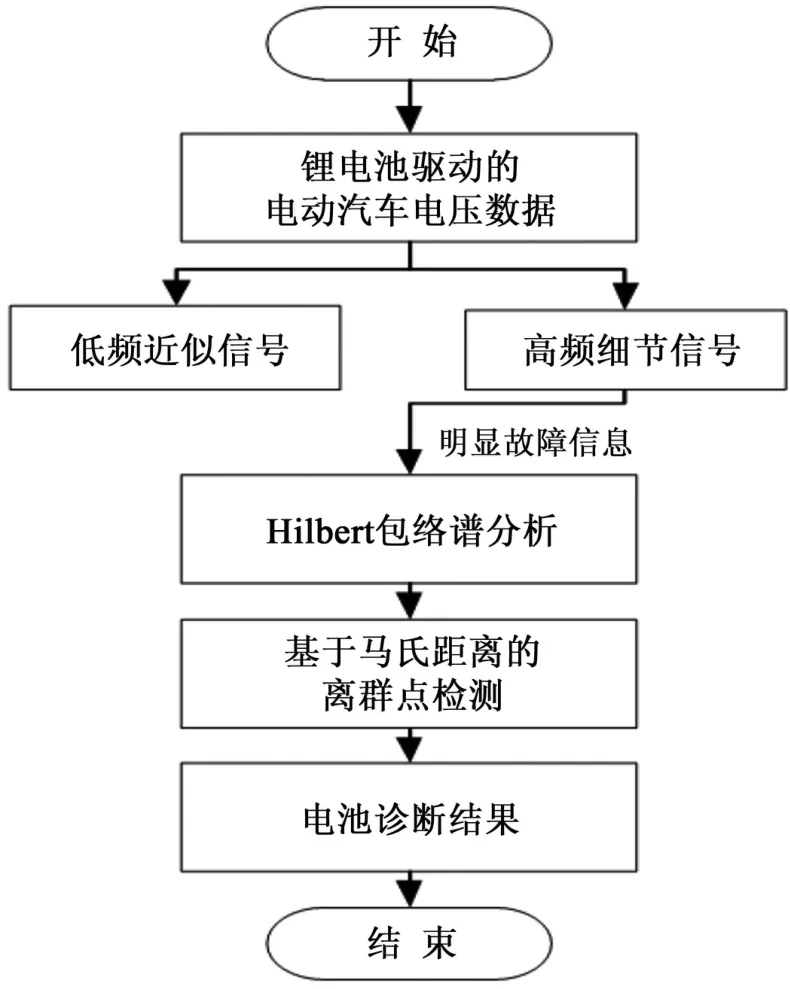
图1 电池故障诊断框图

1.1 小波分解原理

小波变换是信号分析领域常用的一种分析，可以将信号分解为时频信息。它不仅具有良好的时频局部性、有效检测突变信号性，而且还有灵活性等优点[9]。连续小波变换是将时变函数经过伸缩或平移后产生一个函数族（即小波）：

式（1）中：a代表控制伸缩的尺度参数；b代表控制位置的平移参数；φ(t) 代表的是小波基函数。Wf(m,n) 表示信号函数f(t) 的离散小波变换。它的定义式为：

式（2）中：m和n为离散值。离散小波变换原理的本质是信号函数f(t) 被映射到位移尺度平面上的离散点。小波系数Wf(m,n) 表示一种函数分量，即信号函数f(t) 可用部分的小波函数φm,n(t)所代表的一种分量。在实际工程应用中，尤其是数字信号处理领域中，小波变换应用广泛。因为在信号的时频局部化分析过程中，它的频率窗和时间窗都能够发生改变。

图2 所示为信号 U 的整个小波分解过程。信号 U 为单体电池电压信号。当信号 U 经过小波变换之后，分解到第1 层时，获得用 cA1 表示的小波低频近似值和用 cD1 表示的小波高频细节值。然后对 cA1 进行分解，即分解到第2 层，可获得用 cA2表示的小波低频近似值和用 cD2 表示的小波高频细节值。由此通过依次推进，多次分解小波逼近可以获取更多层的小波高频细节值和小波低频近似值[10]。信号 U 分解的层数越多，信号频率越低，小波低频近似值就越小。因为所有离散信号的离散点都是有限的，所以最大分解层数N须满足信号离散点数量大于或等于 2N的要求。将电池的电压信号 U进行小波分解后，发现小波低频近似值处故障信息不明显，但是小波高频细节值能够明显清晰地反映故障信息，因此选取小波高频细节值进行希尔伯特（Hilbert）变换。

图2 信号小波分解过程图

1.2 希尔伯特变换原理

希尔伯特（Hilbert）变换是利用重构解析信号的方法，将测试信号映射到复数空间，得到信号的实部与虚部[11]，也就是让测试信号产生一个 90°的相移，从而与原信号构成一个解析信号。这个解析信号即为包络信号[12]。将一个原始信号u(t) 的Hilbert 变换H[u(t)]定义为[13]

如果把这个定义理解为，u(t)通过滤波器的输出得到H[u(t)]，则原始信号u(t) 的解析信号z(t) 复数解析式为

如果 Hilbert 变换后的信号幅值记为a(t), 那么a(t)定义为[14]

瞬时相位φ(t) 定义为

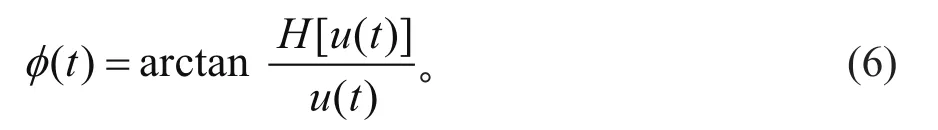
瞬时频率w(t)定义为

1.3 基于马氏距离的异常值检测

异常值检测的常用思路是计算各样本点到样本中心的距离。如果单独某个或多个样本点的距离偏差超过设定的阈值就可以判断该样本点为异常值[15-17]。在本文中，将包络谱平均值特征作为总样本点，并选择马氏距离来衡量样本分布情况。马氏距离表示点与一个分布之间的距离，也可以表示两个未知样本集合的相似度[18-19]。马氏距离求解的过程如下：首先，给定原始样本点xi（i=1, 2, 3….n），用公式

确定样本中心点——样本均值；用如下公式

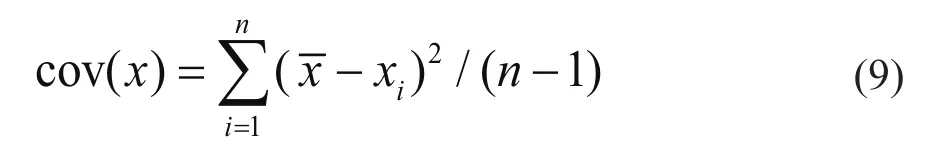
计算协方差矩阵；最后，用公式

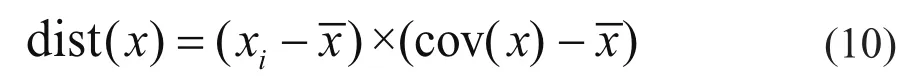
求解每个样本点到样本中心点的距离，即马氏距离。将得到的样本点的马氏距离进行排序，按照异常数据样本点的多少设定阈值。遍历整个原始数据，根据阈值得到异常数据点，并标记该样本点。

2 实验结果与分析

用锂离子电池驱动的电动汽车的预故障数据进行验证，并对结果进行了讨论。以频率 0.1 Hz，分辨率 1 mV，用电压传感器采集信号。利用移动窗口做到确定最早进行异常检测的标准时。如有必要，尽可能多地消除假警报。每 10 s 上传一次电压数据记录，直到触发 BMS 检测的差分电压阈值。然后，出现异常的第27 个电池的后续电压信号以急剧下降的趋势每秒上传一次，最终导致电动汽车在驾驶过程中自燃。本文中使用的汽车预故障数据为从充满电开始放电到电池管理系统报警时刻所采集的数据（如图3 所示）。

图3 电压原始信号

通过分析，利用 Daubechies 5 (db 5) 小波将电压信号进行 2 层小波分解，得到 2 个小波低频近似值和 2 个高频细节值。图4为电池的电压信号进行小波分解后得到的分解图。在 2 个低频近似值处故障信号与正常信号重合率较高，表明由低频近似值不易得到故障电池的信息。然而，在 2 个高频细节值中可以明显判断出故障电池的编号，因此选用小波高频细节值进行希尔伯特变换，从而获取包络谱特征。

图4 电池电压信号的小波分解图

图5 为对不同时间段电压细节信号采用希尔伯特变换获得的包络谱。由图5a 可知，当电池处于正常时间段时，各个电池形成的包络谱之间基本没有区别。然而，从图5b可以清晰看出，第27号电池的包络谱明显与其他正常电池存在偏差，因此可以将其作为故障诊断特征值。

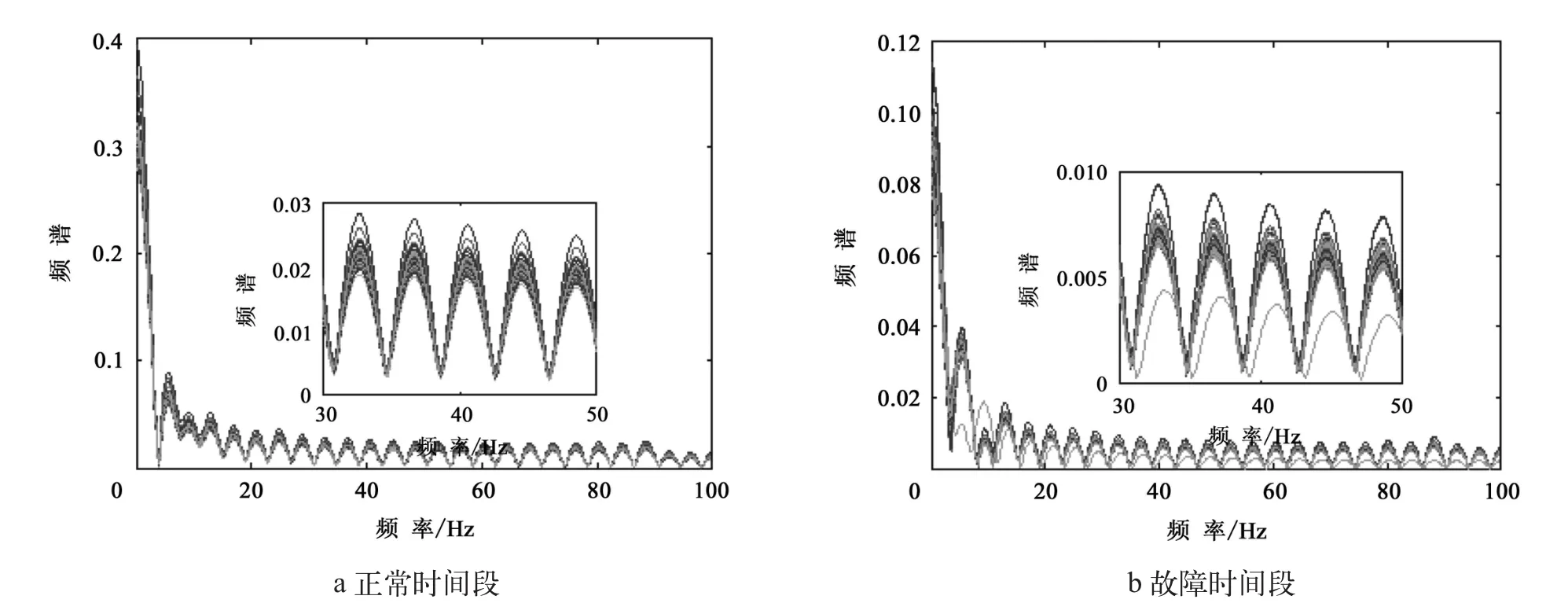
图5 电池电压细节信号包络谱图

图6 为基于距离的离群点检测实现故障诊断的结果图。通过计算马氏距离，设定阈值。遍历整个样本点，大于阈值为异常点记为 1，否则记为 0。从图6中可以明显看到，第27 号电池异常。这与原始数据结果一致，表明该方法在电池故障诊断上是有效的。图7 所示为特征序列异常与原始电压的对应关系。可以看出，原始电压信号是在第460 个采样点出现明显故障，而电池管理系统是在第475个采样时刻才检测到电池出现异常。但是，在第430 个移动窗口以后该方法能够可以进行可信的离群点检测，提前实现故障电池预警。连续的异常值均可以表明，在这些移动窗口中，第27 号电池的电压波形和其他电池的电压波形在趋势上不同。

图6 离群点检测结果

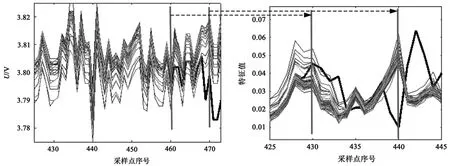
图7 特征序列异常与原始电压信号的对应关系

3 结束语

本文中，笔者通过小波分解选取能够清晰反应故障信息的高频细节信号，之后利用希尔伯特变换获得信号的包络谱，将得到的包络谱特征值作为离群点检测的样本值，最终得到了故障电池的编号。试验结果表明，该方法能够有效地获取电池的故障信息，并且实现提前检测。