快速路合流区交通排放特征研究

俞汪洋，付晶燕，汪 涛，赵 靖

（1.上海理工大学 管理学院，上海 200093；2.中国城市规划设计研究院，北京 100044；3.上海交通大学 船舶海洋与建筑工程学院，上海 200240）

0 引言

随着机动车保有量的不断增加，车辆尾气排放量越来越大，交通排放成为大家热议的话题，交通排放模型和相关影响因素分析也成为研究重点。其中，城市快速路承担着城市主要方向的通勤任务，对社会经济的发展有着巨大影响。正是由于这个原因，许多专家学者重点研究城市快速路的各个方面。快速路系统作为城市的骨干道路，其重要特点为：车辆集中，每天的通行需求巨大，因此会排放大量尾气，特别是快速入口匝道，更是尾气排放的重灾区，快速路的入口匝道往往集中着大量车辆，导致车辆行驶过程中的速度和加速度波动性很大。由于交通排放与速度和加速度密切相关，因此车辆在通过瓶颈路段时会产生大量的尾气排放。

1 研究综述

对于快速路研究的文献有许多，例如孙剑，等[1]研究了快速路交织区通行能力的特点，并结合HCM2010开发了一套快速路交织区的通行能力估算模型；邵长桥，等[2]对快速路瓶颈路段的交通流特性进行了分析；文献[3]-文献[5]研究了快速路瓶颈路段的车头时距分布特征；钟连德，等[6]探讨了用仿真的方法求解道路设施的通行能力；文献[7]-文献[8]基于元胞自动机研究了交织区车辆变道和车道如何分配问题；文献[9]-文献[10]对于交织区汇入行为的影响因素进行了研究；宋国华，等[11]利用浮动车数据，基于比功率研究了快速路排放的分布特点。

对于交通排放模型，国外学者有着很长的研究历史，早在1991 年欧洲加州空气资源委员会就开发出EMFAC模型，但只用于美国加州地区。随后1994年美国环境保护局开发出适用于各州的MOBILE6模型。随着研究的不断深入，又提出许多排放模型，大体上分为宏观模型、中观模型、微观模型三类。宏观模型主要有mobile模型[12]、美国联邦高速公路管理局的CORFLO 模型[13]等；中观模型有CONTRAM[14]和MEASURE[15-16]；微观有CMEM[17]、moves 模型[18]等。早期由于排放数据采集困难，主要是做一些宏观和中观的研究。随着采集设备不断更新换代，对于微观排放模型的研究慢慢成为重点。微观模型以车辆为研究单位，能更加细致地研究每一个排放个体的情况。常见的微观排放模型有CMEM、美国环保署开发的moves模型，以及后面开发的moves2010，这些模型被广泛应用于各个国家。但这些微观排放模型有一个重要特点，需要大量的车辆基本信息，例如moves2010 就需要车辆的车型、使用年限、保养制度等。然而，车辆流动性非常大，无法准确获得相关数据。1999年，麻省理工大学的Jimenz和Palacios提出机动车比功率（VSP）这一概念，用来表示机动车排放与驾驶行为的关系[19]。其中，moves2014 就是基于VSP来估算排放。王岐东，等[20]研究验证了VSP与排放存在着强烈的关联性。孟雄，等[21]研究得出速度、加速度、VSP是车辆排放的核心影响因素。有许多学者采用VSP 来估算排放，秦严严，等[22]基于VSP 估算了自动驾驶条件下的排放情况；高云峰，等[23]采用比功率法建立了一种新颖的反推估计方法，定量估计信号控制交叉口；赖瑾璇[24]、姚荣涵[25]等也采用VSP估计了车辆排放。

总结相关文献可以发现，对于快速路瓶颈路段从安全和效率方面展开研究的有很多，但对于快速路排放研究相对较少，特别是针对快速路交织区排放特点的研究非常匮乏。然而，快速路交织区往往是一个排放的黑点，因此，非常有必要去研究快速路交织区的排放特点。结合交通排放模型的研究现状，以及快速路的车辆往往分布较广、车型多，无法进行精确的排放计算的特点，考虑到排放与VSP之间的密切关系，本文采用VSP对快速路交织区的排放进行估算。为了分析排放与交织区几何、交通流特性之间的关系，决定采用梯度提升树进行模型拟合。

2 基于VSP的交通排放分析

2.1 比功率计算

比功率于1999 年被提出，是一个瞬时的机动车功率与其自身质量的比值。其中轻型车的比功率计算公式见式（1）。

式中：P 表示机动车比功率；v 表示车辆瞬时速度，单位为m/s；a为车辆瞬时加速度，单位为m/s2；s表示坡度。由式（1）可知，比功率是一个瞬时的量，那么就需要划分一定的时间间隔，在文献[21]中，采用秒为间隔进行划分，利用每秒的平均速度和平均加速度代替瞬时速度和瞬时加速度。

在VSP计算过程中，不仅要考虑速度、加速度等变量，也需要考虑坡度的影响，本文研究区域可以认为坡度为0，研究区域如图1所示。为了计算方便与实际数据采集的便利性，忽略匝道坡度的影响，则VSP的算式可以表示为：

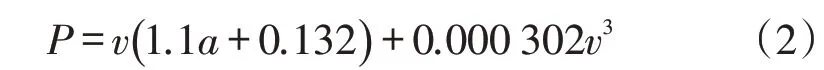
Frey，等[26]采用平均排放率进行聚类分析，获得了每个区间的比功率与具体排放量的对应关系。考虑到国内外驾驶状况的差异，郭栋，等[27]利用实测的排放数据，建立了比功率与实际排放之间的关系，见表1。

依据郭栋等学者的研究，车辆的排放计算见式（3）、式（4）。

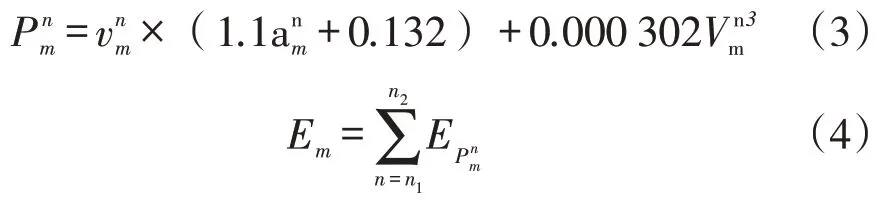
2.2 数据采集与筛选

本文采用来自东南大学UAV团队公开的车辆轨迹数据集中南京应天大街入口匝道的车辆轨迹数据。数据频率为24 帧/s，共采集849 条车辆轨迹，识别精度为100%，研究路段长度为386m。由于数据是基于图像识别获得的，往往会造成一定的误差，因此需要进行数据预处理，具体步骤如下：

（1）采用SG滤波对数据进行降噪；

（2）计算每辆车每秒的平均加速度，考虑到正常情况下车辆的加速度在-5-5m/s2之间，如果不在这个范围之内，则认为该秒有误差，删除该车该秒的数据；

（3）计算VSP 值，参考文献[27]，设定VSP 处于[-40,40]之间，当车辆的VSP超过预设的阀值时，是不合理的，应删除该车该秒的数据。

2.3 不同区域的车辆VSP分布情况

为了探究车辆在不同区域的排放差异，将车辆经过快速路瓶颈路段的轨迹划分为不同区域分别研究。将研究区域按照导流线终点、第一个加速车道终点、第二个加速车道终点的垂直线划分为4 部分，如图1所示，分别计算车辆在不同区域的VSP和排放量。

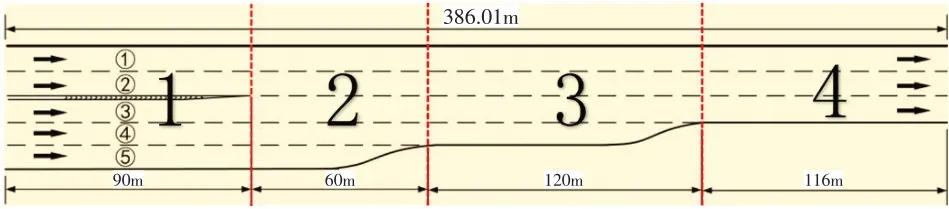
图1 南京市双门桥快速路入口

采用车辆各个区域的平均速度和平均加速度进行VSP 计算，获得车辆经过不同区域的VSP 的分布情况，如图2所示。

从图2可以看出，车辆在经过快速路瓶颈路段的各个区域时，VSP 呈正态分布，大部分车辆的VSP 分布在[-20，20]之间，不同区域分布有差异，这也比较符合人们的认知。

图2 不同区域VSP分布图

VSP的计算是基于车辆的速度和加速度，速度的大小很大程度上决定着其计算结果。为了更好地展示车辆速度在不同位置和不同时间的分布情况，做出如图3所示的速度时空分布图。由图3可知，车辆在到达导流线终点前后的速度要大于车辆在其它位置的速度。同时可以看出，车速在时间上呈现条状分布。

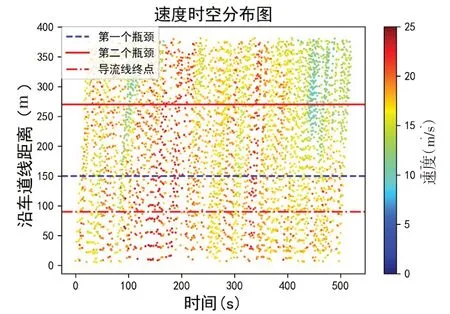
图3 沿车道方向线方向车辆速度的时空分布图

本文选择以CO作为计量标准，计算得到车辆通过合流区域平均的排放因子是3.06（mg/s）。为了分析车辆通过不同车道的排放特点，统计车辆通过不同车道的单位排放量、总排放量、运行时间、平均速度，见表2。

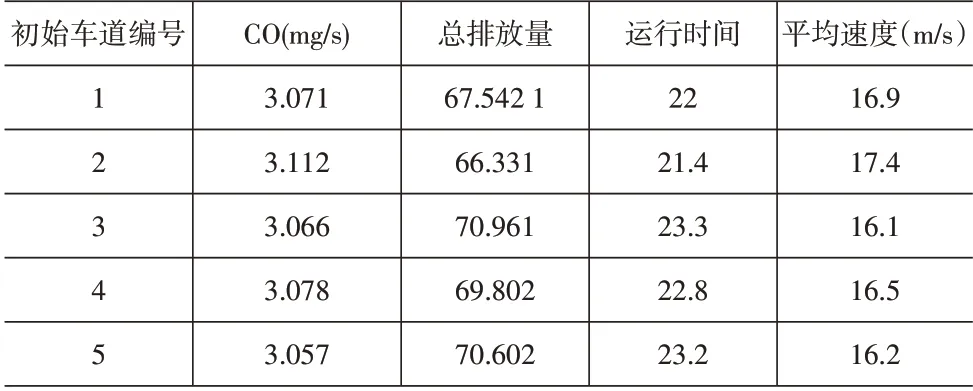
表2 基本数据统计表

从单位时间的车辆排放情况可以看出，2号车道的单位排放要大于其它车道，但总的排放量是最小的，可见2 号车道车辆受到的影响小，车辆能保持较高速度行驶，即从2号车道通过合流区域较为合理；3号车道靠近汇入车道，受到的影响最大，产生的排放量最大，因此。建议车辆在合流区域时，主线车辆可选择从车道2 通过。两条支线车道基本上差异不大，从哪条车道汇入都可以。

2.4 换道行为对车辆排放的影响分析

当车辆在快速路合流区行驶时，从匝道进入的车辆往往要在匝道汇入主线，这也是快速路合流区的一个重要特点。为了探究车辆在瓶颈路段换道行为是否会对车辆的VSP 产生影响，必须研究车辆的换道过程，通常车辆的换道过程大致分为三个环节，分别是换道前的准备阶段、换道阶段、恢复正常驾驶阶段，整个过程如图4所示，只需要确定车辆的开始换道时刻（t1时刻）与车辆恢复正常驾驶时刻（t2时刻），以及车辆跨过车道线的时刻，即可了解车辆的整个换道过程。

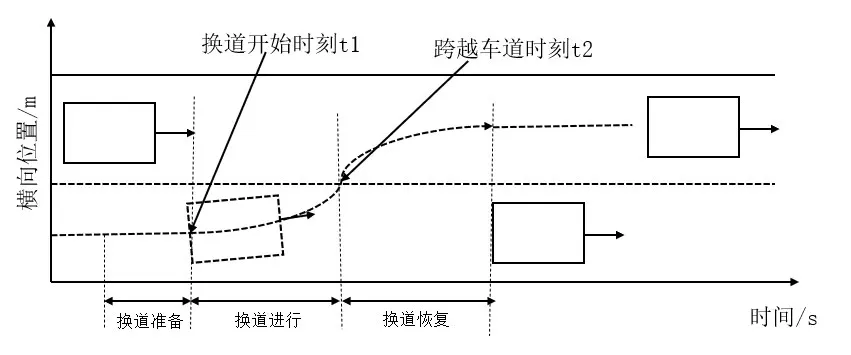
图4 车辆换道行为示意图

（1）确定换道时刻。已知车辆在每一时刻的车道编号，依次判断相邻时刻的车辆编号是否一样，若车辆的车道编号不一致则存在换道；否则，则保持现有车道。

（2）确定换道开始时刻与恢复车辆正常行驶状态时刻。如图5所示，从A-O为车辆的换道开始时刻与跨道时刻，车辆在开始换道时刻，车辆方向角（车辆的行驶方向与车道线的夹角）为0 度，在车辆从A时刻到O时刻的过程中，车辆的方向角不断变大，则车辆到达跨道换道前的最后一个方向角为0的时刻，即为车辆的换道开始时刻。同理也可以获得车辆换道恢复时刻。

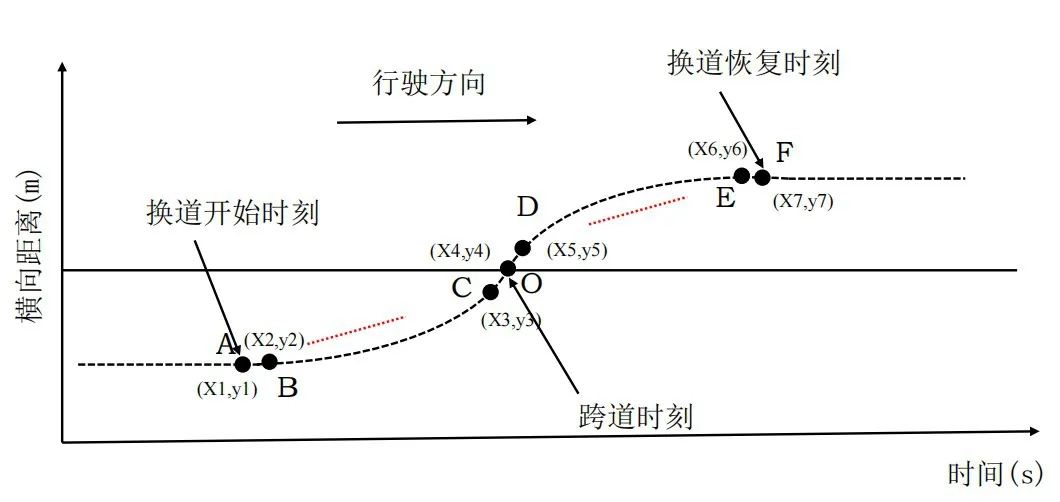
图5 识别换道全过程

为了简化这个过程，本文默认车辆的换道行为持续时间为4s，即研究的时间段为[t2-2，t2+2]。分别提取车辆跨越车道时刻前后2s 的车辆轨迹进行研究。提取获得2 号区域中车道5 换道车辆59 辆和3号区域车道4 换道车辆168 辆在车辆跨越车道线前后2s 的车辆轨迹，同时为了比较换道车辆与不换道车辆的差异，提取相同区域不换道车辆的4s 车辆轨迹进行对比分析。

由图6可知，车辆换道过程的VSP也呈明显的正态分布，VSP 分布在[-50，50]之间，同时也可以发现车辆更加集中于在车道5终点位置进行换道。

图6 车辆换道过程VSP分布图

为了比较换道过程与正常行驶过程以及在哪个区域换道的VSP是否存在差异，特绘制表3，由表3可知，车辆在区域二和三换道VSP较小，车辆在区域三的VSP 明显小于其它区域，车辆通过区域二和三的均值为0.436 2，明显小于车辆在换道过程的均值。

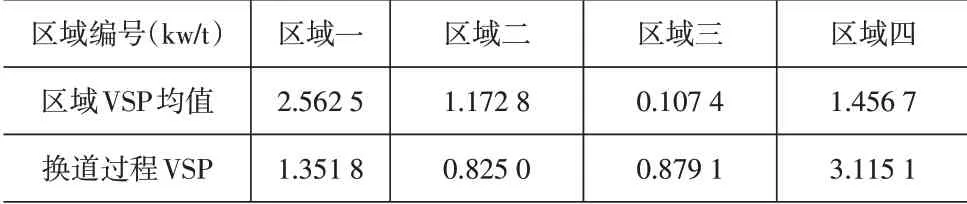
表3 不同区域VSP均值

3 基于GBDT 的车辆瓶颈路段排放估计模型

为了探究车辆经过快速路合流区的车辆排放因子与其影响因素之间的关系，本文采用梯度提升树（GBDT）算法[28]进行建模，分析各个影响因素对于排放因子的贡献情况以及排放因子随主要影响因素的变化趋势。

3.1 GBDT模型介绍

GBDT算法是一种采用决策树的集成模型，通过多个决策树不断优化结果，即可用于分类也能用于回归，这种方法采取连续造树，不断减少结果的残差，以到达模型效果的最优。相对于随机森林更加高效，GBDT 算法是一个很强大的回归模型，这种算法最大的好处是可以较好地预防过拟合现象。本文采用GBDT 算法探究每个影响因素对于结果的相对权重，其基本思想是通过前向分步算法（将决策树串联起来，逐步优化）多轮迭代生成多棵残差子决策树，使得子决策树有输出，并越来越逼近最终的决策目标。因此，提升树在机器学习算法族的应用中具有很高的准确率[29]。

GBDT算法流程如下，其中L( )yi,f(x)表示损失函数，J表示每颗回归树叶子节点数，gm( )x表示回归树，m表示第m棵树，bjm、lr、I分别表示常量、学习率、激活函数。

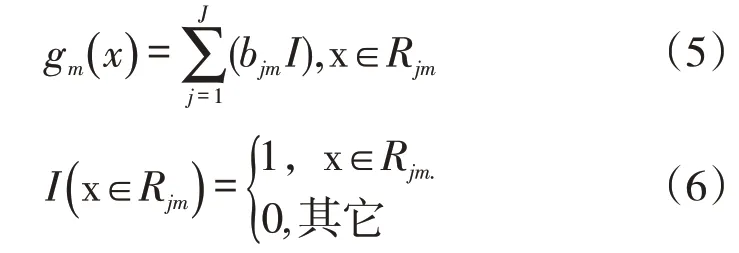
步骤1：模型的初始化：

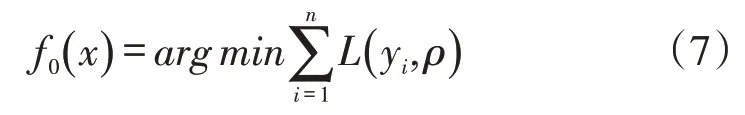
步骤2：迭代生成回归树

（1）计算所有样本的损失函数的负梯度值，将其作为残差rim的估计值。

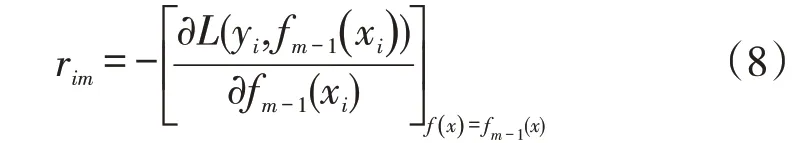
（2）针对（1）的残差估计值，生成回归树，再计算梯度下降的步长：

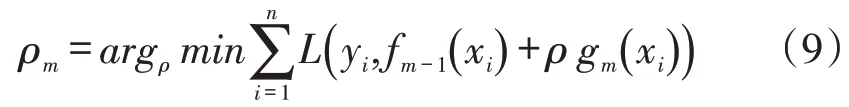
步骤3：更新模型

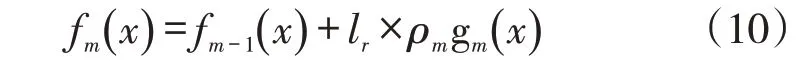
步骤4：输出模型fm(x)。本文采用python 中Skilearn 库的GBDT 回归树算法，模型的准确度受到损失函数、回归树深度、学习率、叶子节点数量的影响。考虑实际情况，本文所选择的损失函数为最小绝对值误差，回归树的深度为3，学习率为0.01，叶子节点的个数为3。

3.2 影响因素选择

车辆在匝道合流区域行驶时，往往在运动学、空间位置、交通流特性上存在较大差异，本文从这三个角度提出影响车辆排放的影响因素。

（1）车辆运动学因素包括加速度、速度的影响，提取车辆的平均速度、平均加速度、进入速度、离开速度、是否有换道行为等因素；

（2）空间位置上的因素，如车道编号、区域编号；

（3）交通流特性，如最大占有率、平均占有率，其中，车辆的占有率计算如下：

式（11）中，t1和t2分别表示车辆到达和离开时刻，m0和m1分别表示研究区域的面积和每辆车的平均面积，ni表示i时刻在研究区域内的车辆数。具体影响因素见表4。

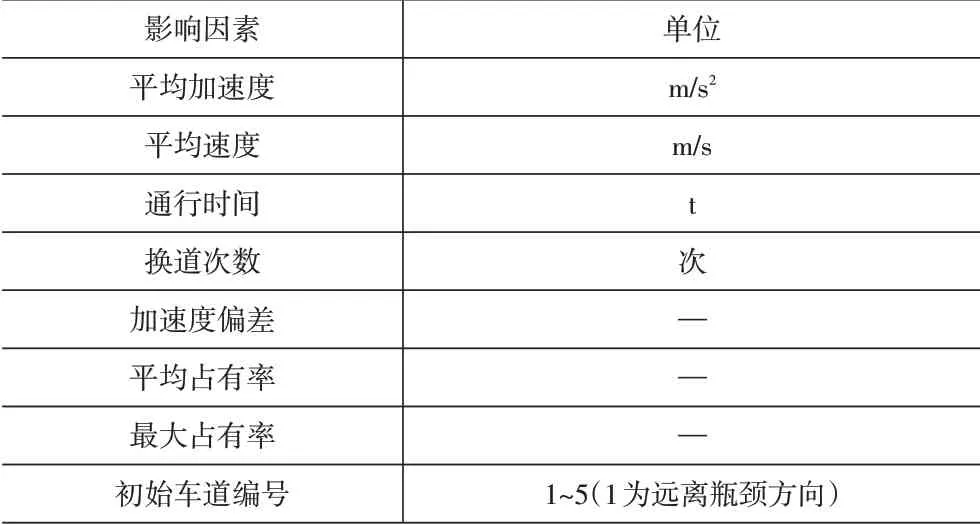
表4 影响因素

3.3 模型拟合与评价

设定训练集和验证集的车辆分别为462辆和116辆，模型结果见表5。

从表5可以看出，模型的拟合效果很好。为了分析各个因素对于最终结果的贡献情况，因此绘制影响因素贡献图，如图7 所示。由图7 可知，影响车辆单位时间排放量的主要影响因素是平均加速度、平均速度、平均占有率等，与许多学者的研究中都认为车辆的排放与速度和加速度密切相关一致，可见本文的模型符合已知结论。其它如换道次数多少也产生一定的影响，但影响很小，分析可能是换道过程持续的时间很短，对于车辆通过整个合流区域的影响不大。平均加速度与平均速度对于车辆的单位排放有很大的影响，因此，对于平均速度与平均加速度进行敏感性分析。由图8和图9可知，排放因子随平均速度的增加慢慢趋于平缓，平均速度小于17m/s 时，车辆的排放因子与平均速度呈正相关。平均加速度与排放因子呈现正相关，加速度行为比减速行为导致更大的排放因子。

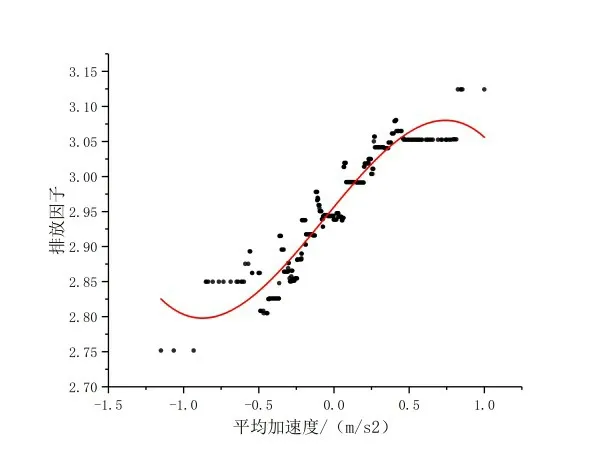
图8 平均加速度与排放因子的关系图

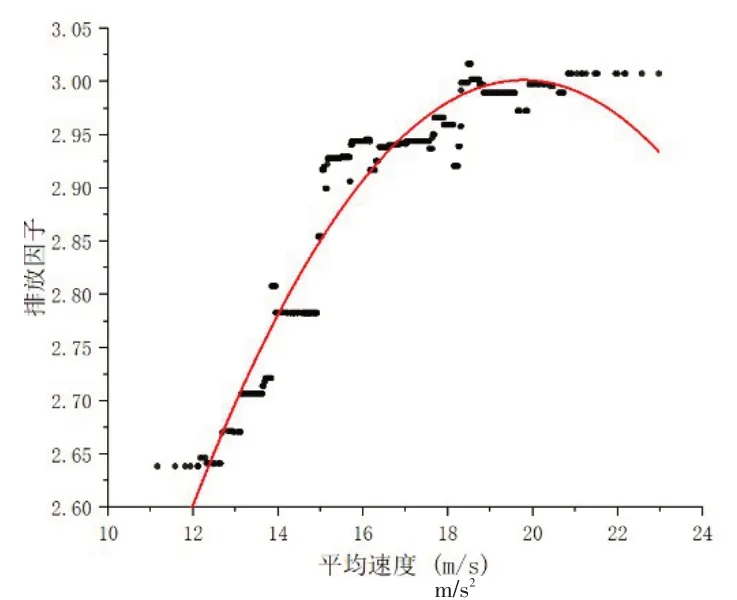
图9 平均速度与排放因子的关系图

表5 模型评价

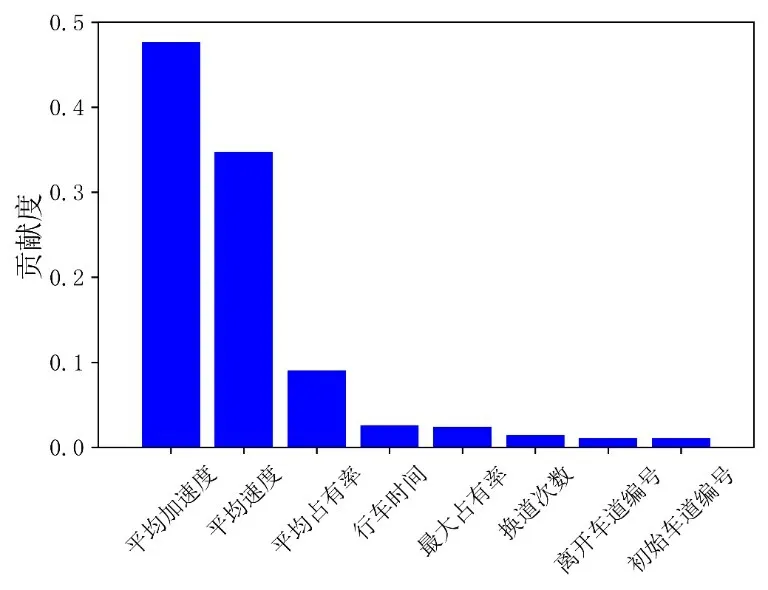
图7 影响车辆单位时间排放量贡献率