基于Copula函数的深圳市雨潮遭遇风险分析

石赟赟，姚航斌,2，万东辉，郑新乾

(1.珠江水利委员会珠江水利科学研究院，广东 广州 510630；2.河海大学水文水资源学院，江苏 南京 210098；3.珠江水利委员会水文局，广东 广州 510611)

在快速城市化和全球气候变化的共同影响下，中国城市极端洪涝事件频发，严重影响城市的建设与发展。内陆城市洪涝主要受降水、地形、防洪排涝系统等因素的影响，滨海城市则需综合考虑潮位变化对内河洪水和城市涝水的顶托[1-2]。降雨与潮水遭遇将导致城市积水难以排除，加剧城市洪涝灾害，严重影响城市生活生产[3-4]。为了进一步提高滨海城市防洪排涝能力，加强韧性城市建设，综合考虑暴雨与潮位双变量遭遇的工况具有重要的现实意义[5]。

雨潮遭遇问题，本质上是双水文变量的遭遇问题，其常见的研究方法是基于Copula函数建立双水文变量的联合分布模型，计算双水文变量遭遇的同现概率、条件概率等。Copula函数能客观地描述水文事件间的相关性，准确分析水文频率，提高多变量水文事件设计精度[6]。目前，Copula函数在洪水遭遇、水文预报不确定性、丰枯遭遇和洪潮遭遇等问题上已有大量的应用实例[7-8]。在雨潮遭遇的研究方面，Lian等[9]通过Copula函数建立暴雨与潮位联合风险概率，优化了福州市防洪排涝设计。武传号等[6]基于Copula函数构建广州市年最大1 h降雨量与年最大潮位、年最大潮位与相应1 h降雨量以及年最大1 h降雨量与相应潮位3种联合分布概率模型，计算分析了广州市雨潮遭遇的风险。黄国如等[10]应用Copula函数构建了历史与未来广州市雨潮遭遇风险概率分布模型，分析了在不同排放情景下，广州市雨潮遭遇概率的变化趋势。张卫国等[11]采用G-H Copula函数构建甬江流域暴雨和河口相应潮位的联合分布，计算了同现、条件概率，并根据条件最可能组合原理，推求了给定某一设计暴雨情景下，潮位的最可能值和置信区间。杨帆等[12]基于采用Copula函数，构建了佛山市年最大 1 h 降雨量与相应潮位以及年最高潮位与相应1 h降雨量的联合分布，定量评估了佛山市城区多种雨潮组合下遭遇概率。

综合雨潮遭遇近年来的研究成果，雨潮遭遇主要分为年最大降雨遭遇相应潮位、年最大潮位遭遇相应降雨和年最大降雨遭遇年最大潮位。年最大降雨遭遇相应潮位的联合分布贴合实际，但在防潮标准制定时一般使用年最大潮位为设计依据；而年最大潮位发生时，相应降雨可能为0 mm；年最大降雨遭遇年最大潮位的情况过于极端，与实际工况不符。为了更好地模拟雨潮遭遇，本文基于深圳市1967—2018年年最大1 d降雨量及其赤湾站相应潮位资料，采用Copula函数分别构建最大1 d降雨与相应潮位联合分布模型，将相应潮位转换成对应的年最高潮位，分析深圳市的雨潮遭遇的风险，为防洪潮工程设计提供更合理的依据。

1 研究方法

本文基于Copula函数构建深圳市赤湾站最大1 d降雨与相应潮位的联合分布模型，计算分析深圳市雨潮遭遇的风险，主要步骤包括降雨及其相应潮位的相关性，降雨与潮位各自边缘分布的确定，基于Copula函数的降雨及其相应潮位联合分布构建，最优拟合Copula函数的选定以及雨潮遭遇风险计算与分析。

1.1 Copula函数定义与分类

Copula能将多个不同变量的边缘分布连接成一个联合概率分布函数[13]。根据Sklar定理，Copula函数具有唯一性[14]。以二维Copula为例，对于一个具有连续边缘分布函数u和v的二维联合分布函数H(x,y)，则存在唯一的一个二维Copula函数C，使得H(x,y)=C(u,v)[15]。

Copula函数通过构建多水文变量的联合分布，能够有效简化多个水文变量间相关关系分析的复杂度，因此，其在水文领域得到充分运用[16]。其中Archimedean Copula函数由于构造方法简单，模拟效果较好，在实际应用中最为广泛。Archimedean Copula中最常见为G-H Copula、Clayton Copula和Frank Copula 3种，其函数形式见表1。

表1 常见的Archimedean Copula函数形式及参数范围

1.2 相关性分析和边缘分布确定

在采用Copula函数构建水文变量联合分布前，需对水文变量进行相关性分析，并确定边缘分布[17]。水文变量间的相关性分析常用方法有Pearson线性相关系数、Kendall相关系数和Spearman相关系数，其中Pearson线性相关系数衡量的是线性相关关系，相关系数越接近于1或-1，线性相关度越强；Kendall和Spearman相关系数均为秩相关系数，其检验变量无需服从某种特定分布，适用范围相较于Pearson线性相关关系更为广泛，相关系数越接近于1或-1，表明变量间相关度越强。

确定边缘分布主要是基于假设检验，该方法通过对某种分布的拟合结果进行假设检验，从而确定边缘分布，其应用过程繁琐，步骤较多。因此，本文拟采用核分布估计法确定边缘分布。核分布估计法是常见的非参数估计方法之一[18]，省去了假定变量服从某种特定分布模型的环节，直接使用实测样本资料来研究多变量之间的相关结构，且估计结果更贴近于实际情况。

1.3 Copula函数拟合优度检验

不同的Copula函数拟合同一多变量水文事件时存在明显的拟合差异，为了选择出拟合效果最佳的Copula函数，必须对拟合结果进行拟合优度评估。常用的评估方法有均方根误差和信息准则[19]，和值越小，表明拟合结果越好。其原理如下：

(1)

(2)

(3)

(4)

1.4 雨潮遭遇风险计算

本文采用同现风险概率、条件风险概率、组合风险概率以及防涝风险概率[6,11,20-21]综合表征区域的雨潮遭遇风险。其中同现风险概率是表征雨潮同时超过某一设计值的概率；条件风险概率是描述在降雨量达到某一设计值的条件下，遭遇大于某一设计值潮位的概率；组合风险概率是在不超过某一设计值的降雨量发生的条件下，遭遇超过某一设计值潮位的概率；防涝风险概率是分析降雨量或潮位超过某一设计值发生的概率。其计算公式如下。

同现风险概率：

P(X>x,Y>y)=1-u-v+C(u,v)

(5)

条件风险概率：

(6)

组合风险概率：

(7)

防涝风险概率：

P(X>x或Y>y)=1-F(X,Y)=1-C(u,v)

(8)

式中X——降雨量，mm；x——降雨设计值，mm；Y——潮位，m；y——潮位设计值，m；u——降雨量的边缘分布；v——潮位的边缘分布。

2 实例分析

2.1 研究区域

深圳市地处珠三角的西南角，北连惠州、东莞，南隔深圳河与香港九龙新界毗邻，东依大鹏湾、大亚湾，西濒伶仃洋与珠海市相望。深圳市系以丘陵为主，低山、台地、阶地、平原相结合的综合地貌区，具有典型的三角洲河口滨海城市特征。整体上深圳市呈东西宽、南北窄的条带状分布(图1)，总面积为1 997.47 km2，其中建成区面积927.96 km2。

深圳市属亚热带海洋性气候，雨量充沛。根据《2019深圳市水资源公报》，深圳市多年平均降雨量1 830 mm，降雨时间、空间上分布不均，降雨量东南地区多、西北少，且主要集中在4—10月的汛期。

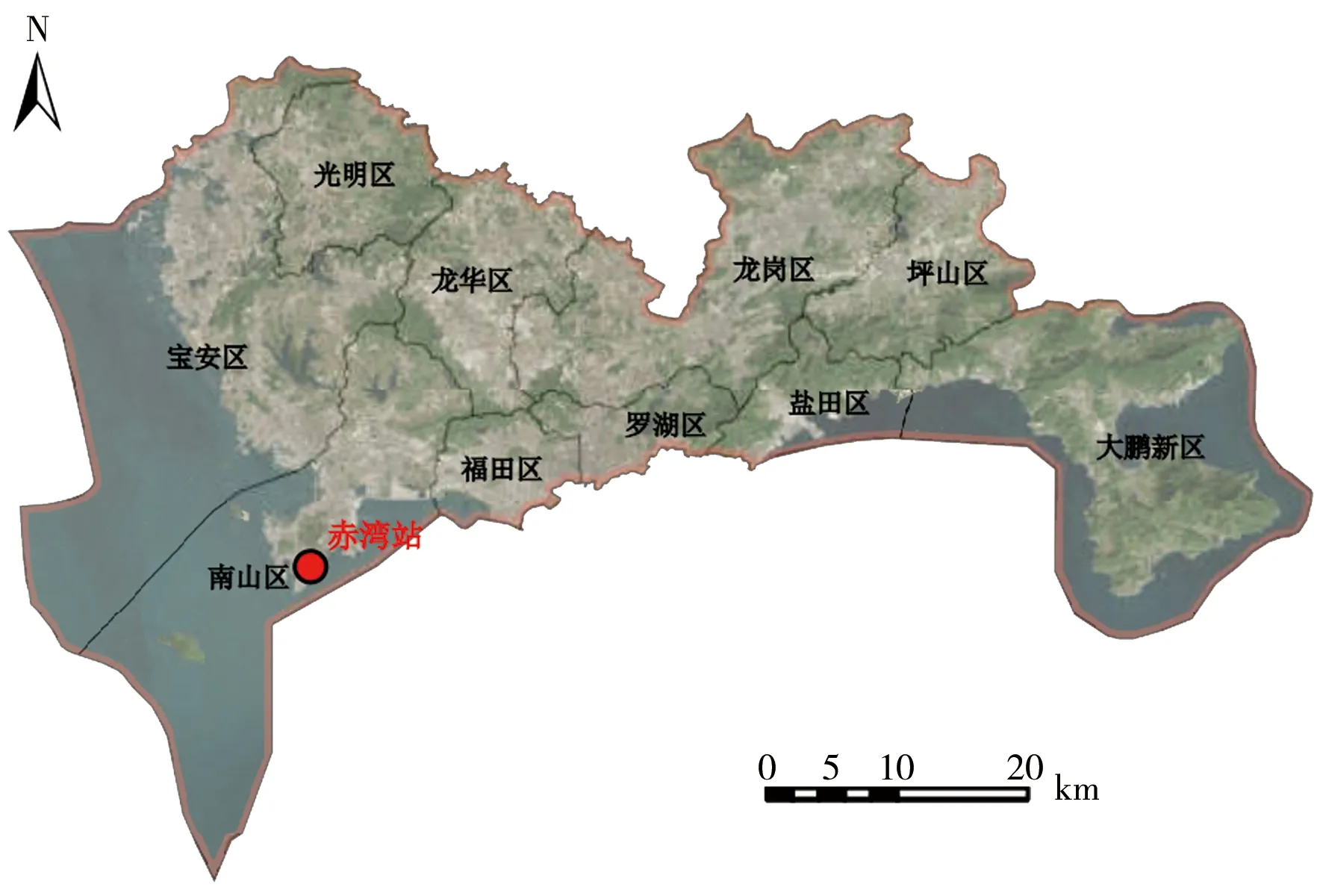
图1 深圳市赤湾站位置

2.2 联合分布模型建立

2.2.1相关性分析和边缘分布确定

基于SPSS软件，采用Pearson线性相关系数、Kendall相关系数和Spearman相关系数对深圳市赤湾站最大1 d降水量与其相应潮位进行相关性分析，得到赤湾站最大1 d降水量与其相应潮位的Pearson线性相关系数、Kendall相关系数和Spearman相关系数分别为0.343、0.228、0.341，表明深圳市赤湾站年最大1 d降雨与其相应潮位具有一定的相关性，可以依托Copula函数构建联合分布模型。

在构建联合分布前，需确定年最大1 d降雨量和其相应潮位各自的边缘分布。本文采用核分布估计法，以Matlab软件作为计算工具确定最大1 d降水量及其相应潮位各自的边缘分布，得降雨及潮位的分布见图2、3。

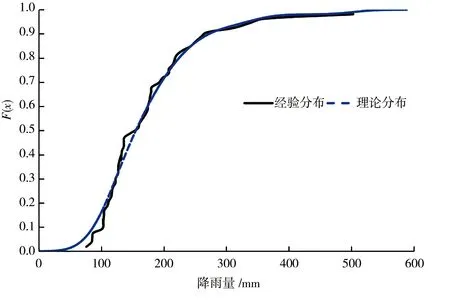
图2 赤湾站年最大1 d降雨量的经验分布与理论分布拟合

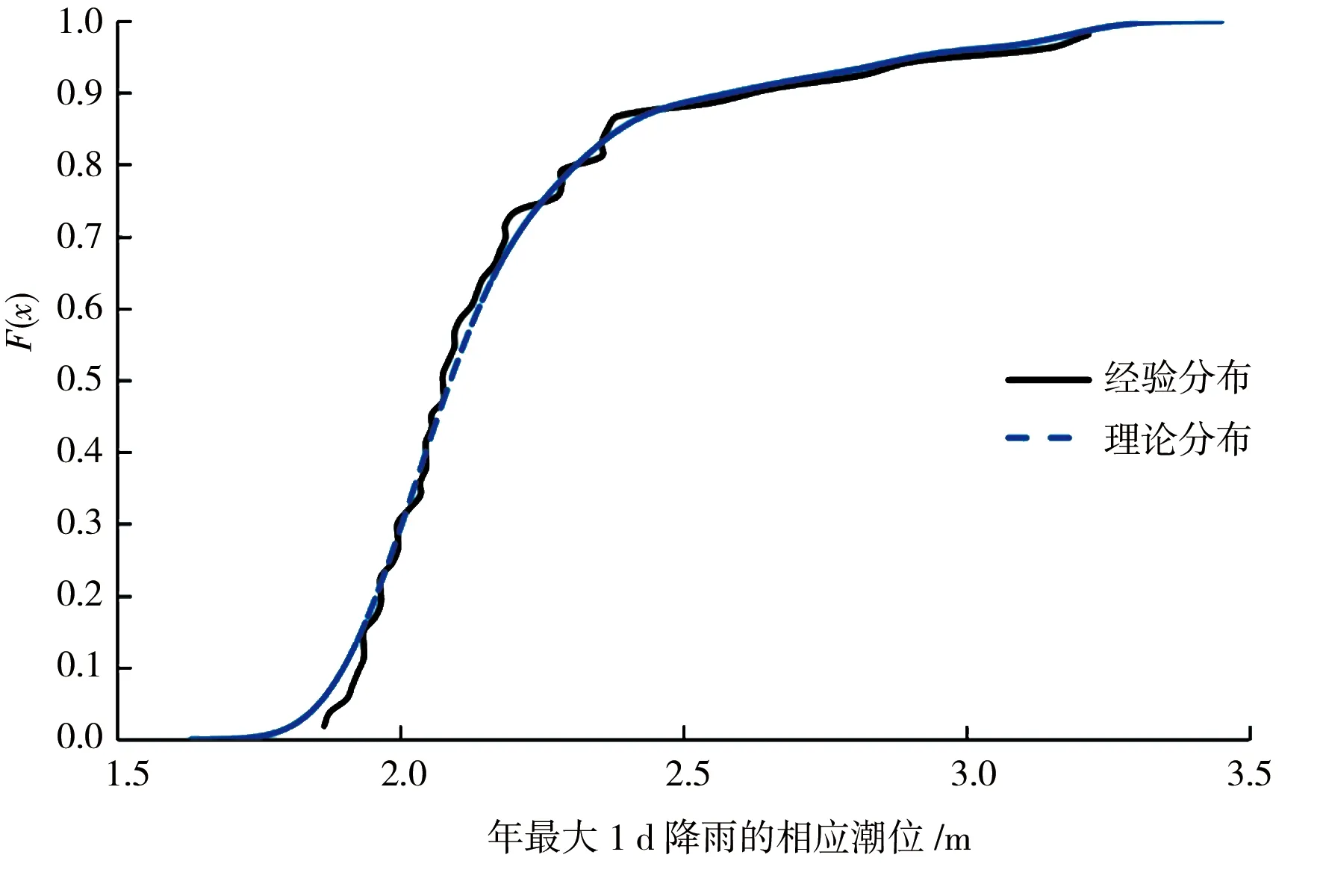
图3 赤湾站年最大1 d降雨量相应潮位经验分布与理论分布拟合

2.2.2Copula函数优选

基于G-H Copula、Clayton Copula和Frank Copula函数构建最大1 d降水量及其相应潮位联合分布模型，采用极大似然估计法估计3种Copula函数的参数，并计算了3种Copula函数的均方根误差和值，结果见表2。

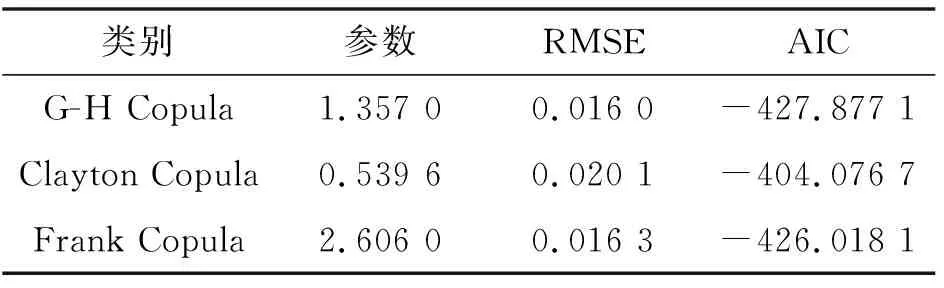
表2 Copula函数的参数、RMSE和AIC

根据表2的定义，G-H Copula函数的和值均为最小，说明G-H Copula函数的拟合结果较好。因此，本文采用G-H Copula函数构建深圳市赤湾站年最大1 d降水量及其相应潮位的联合分布，见图4。

图4 深圳市赤湾站年最大1 d降雨量与其相应潮位的G-H Copula函数分布

2.3 雨潮遭遇风险

参考深圳市相关防洪防潮规划，深圳市的内涝防治标准为100年一遇，赤湾附近的现状海堤防潮工程设计标准大多为200年一遇。因此，选取年最大1 d降雨的设计重现期为10、20、50、100、200 a，选取最高潮位的设计重现期为100、200、500 a。根据式(5)—(8)，分别计算不同重现期组合的雨潮遭遇风险概率，计算成果见表3。

由表3可知，同现风险概率和防涝风险概率均随着年最大1 d降雨或相应潮位的重现期减小而增大，呈负相关关系，如10年一遇的年最大1 d降雨(272.7 mm)遭遇256.51年一遇的相应潮位(3.237 m)时，同现风险概率和防涝风险概率均为最大，分别为0.31%、10.08%；条件风险概率和组合风险概率均为条件概率，某一重现期的年最大1 d降雨发生的条件下，遭遇重现期越小的潮位条件风险概率和组合风险概率越大，如重现期为200年的年最大1 d降雨(521.5 mm)发生的条件下，遭遇重现期为256.51 a的相应潮位(3.237 m)的条件风险概率和组合风险概率最大，分别为29.48%、0.24%；同时，重现期发生越大降雨的条件下，遭遇某一重现期的相应潮位的条件风险概率和组合风险概率越大，如降雨重现期从10年一遇上升至200年一遇(即降雨从272.7 mm上升至521.5 mm)，遭遇到256.51年一遇相应潮位(3.237 m)的条件风险概率从3.10%上升至29.48%，组合风险概率从0.08%上升至0.24%。

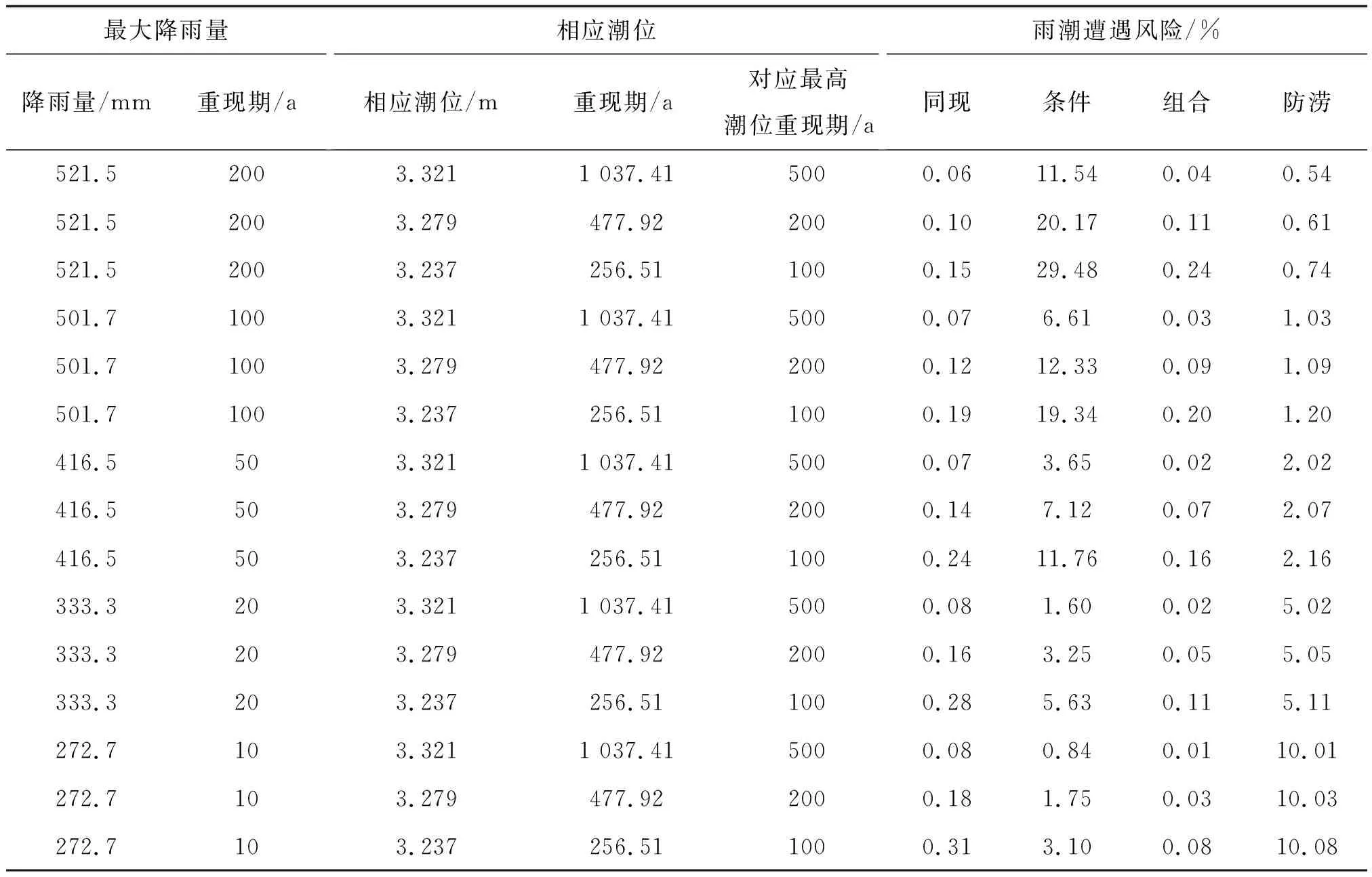
表3 不同重现期组合下的最大降雨量遭遇相应潮位的风险概率

根据深圳市现状内涝标准与堤岸防潮能力，深圳市超标准(100年一遇)年最大1 d降雨(501.7 mm)与超标准(200年一遇)的最高潮位(3.279 m)同现风险概率为0.12%，表明深圳市超标准的降雨与潮位同时发生的重现期接近千年一遇；在未发生超标准降雨情况下，发生超标准潮位的风险概率仅为0.09%，这意味着未发生超标准降雨时，防治内涝的重心在于城市的排水和排涝河道行洪；超标准降雨或潮位任意一个发生的概率为1.09%，小于100年一遇，且在超标准降雨发生的条件下，遭遇超标准潮位的条件风险概率为12.33%，同时，随着降雨增大，遭遇超标准潮位概率随之增大，因此，在深圳市实际防洪潮工作中，应重点关注超标准降雨发生后的潮水顶托风险。

3 结论

本文基于Copula函数计算分析了深圳市雨潮遭遇风险。主要结论如下。

a)对比基于核分布估计的年最大1 d降雨及其相应潮位的边缘分布构建的G-H Copula、Clayton Copula和Frank Copula函数的联合分布拟合结果，G-H Copula函数对于深圳市赤湾站的降雨及其相应潮位的拟合精度最优，结果更为可靠。

b)深圳市超标准降雨与潮位同现的风险概率较小；未发生超标准(100年一遇，即501.7 mm)降雨时，遭遇超标准潮位(200年一遇，即3.279 m)的组合风险概率较小，因此，在未发生超标准降雨时，防治内涝的重心应在于城市内部的排水排涝；但在发生超标准降雨后，遭遇超标准潮位的概率较大，且随着降雨量级的增大，遭遇超标准潮位概率也随之增大，因此深圳市在遭遇超标准降雨时，应及时做好防潮工作。