思直观之源 展想象之翼
祝敏芝
(浙江省台州市三门县教师发展中心 317100)
《辞海》中“直观是不经过理智推理过程,而由感觉或精神直接体验的一种认识作用”,“想象是人在头脑里对已储存的表象进行加工改造形成新形象的心理过程.”康德认为:一切人类认知都是从直观开始,从那里进到概念,而以理念结束.直观想象是一种重要的思维方式,也是数学认知的重要环节,在教学中如何引导学生建构直观展开想象是值得研究和关注的问题.
1 直观想象的含义
《普通高中数学课程标准(2017年版)》指出,“直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.主要包括:借助空间形式认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路.”[1]徐利治先生认为,“学习一条数学定理及其证明,只有当我能把定理的直观含义和直观思路弄明白了,我才认为真正懂了.……在数学中,我宁愿把直观一词解释为借助于经验、观察、测试或类比联想所产生的对事物关系直接的感知与认识.”[2]F.克莱因在《高观点下的初等数学》中指出:“空间观念的起源有两个,一个是对空间观念的直觉,可以通过量度而直接意识到.另一个是主观的理想化的直觉,它超越感官观察的不精确性.”[3]首都师范大学朱一心教授在《数学的可视化直观》的演讲中提出,“数学直观主要体现为数感、空间观念与几何直观,还有公众不太知道的一种可操作或可实现的‘关系’与‘程序’,能引起对数学某种知识和理论的联想、感悟,从而把知识理解成一种我们可以了解的直观.” 张广祥、张奠宙指出代数教学中的模式直观,并将模式直观分为常识性、迁移性、和谐性、符号性四种[5].冯静、许亚桃、吴立宝提出“学生几何思维的直观、描述、理论三个水平对应着直观想象素养的三个层次:原型直观、表象直观和想象直观.”[6]
数学直观表现方式主要有关于事物空间形式的感知、关于事物背景意义的认识以及关于事物逻辑关系或形成发展秩序的感悟.数学想象是借助经验、观察、实验、直觉归纳与类比联想等思维方式,寻找直观的空间形式、直观模型或直观形态,把握和理解比较抽象、深刻的思维对象.
2 直观想象的途径与方式
2.1 基于量度的图形直观
如,a-b表示两个数的差,也可以理解为两条线段的长度之差,其绝对值也是数轴上两点之间的距离,这样两数差就有了直观的意义.基于度量的数形转换与基于坐标的数形结合是量度的两种最主要的途径与方式.
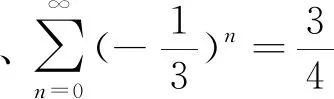

图1
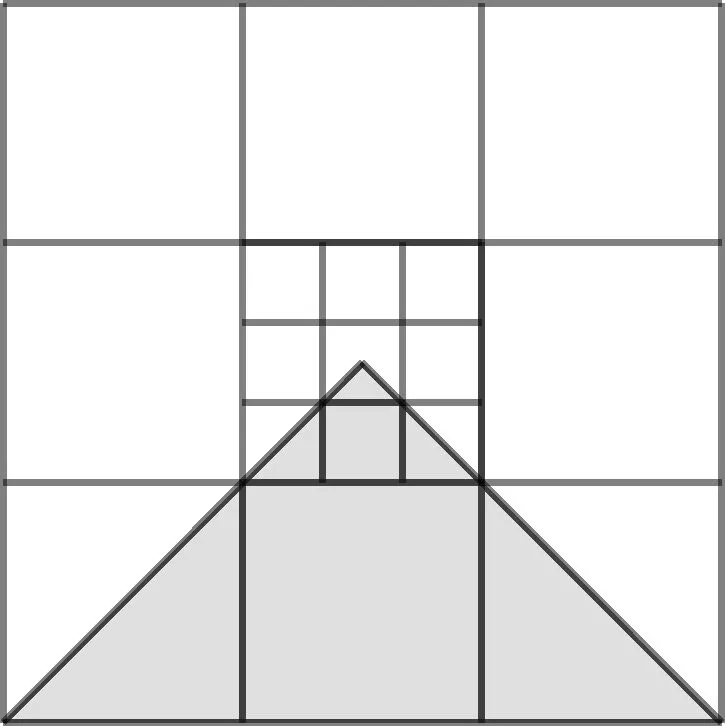
图2
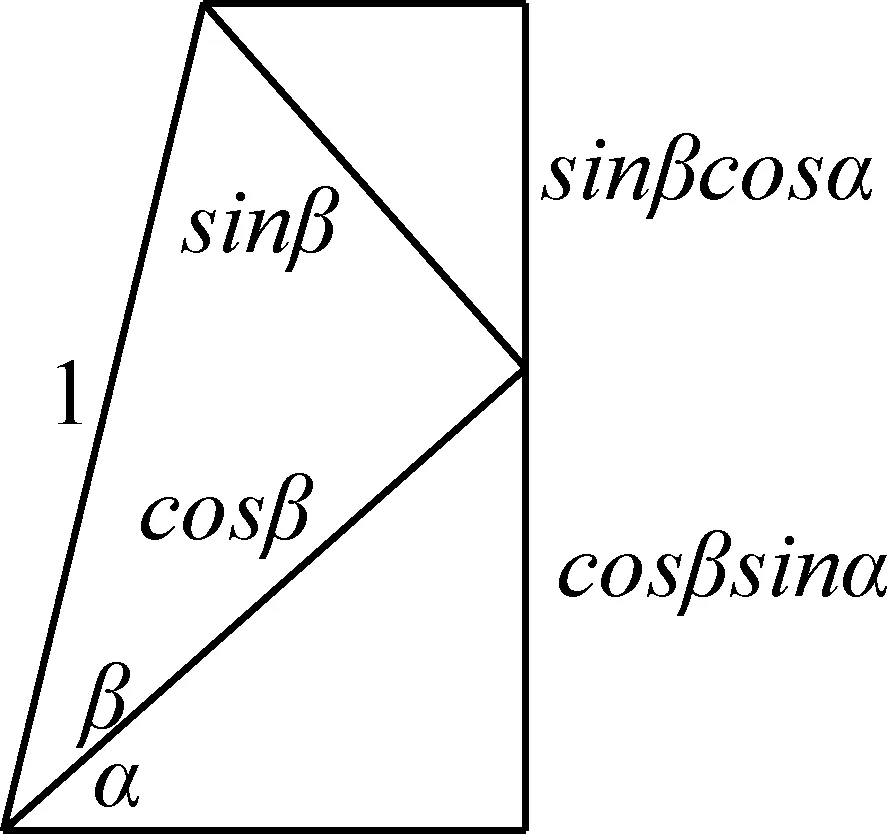
图3


图4
2.2 基于具象的模型直观
表象是保持在记忆中某一事物的形象,是感知、记忆的结果;具象是根据个体的需要、态度、体验和思想观念来综合取舍表象进而形成的表象结果.

图5
二是符号化模型.符号化是人类对信息最强有力的压缩加工方式,通常有数学语言、符号或图表等等.如,任何6个人中必有3人相互认识或者3人相互不认识.6个人用6个点表示,认识用实线连结,不认识用虚线连结,则从某个人A出发与另外五个人连结的线中至少有三条AB、AC、AD同为虚线或同为实线(不妨设为实线),如图5,这四个人的连线中必存在同为实线或同为虚线的三角形.又如欧拉将七桥问题提炼为一笔画问题,创立了图论.美国数学家斯蒂恩说:“如果一个特定的问题被转化为一个图式,那么思想就整体地把握了问题,并且能创造性地思索问题的解法.”[7]
2.3 基于经验的关系直观
还有一种直观超越图形、具象等知觉的局限,是一种基于经验的精神体验与认识的直观.F.克莱因认为运算法则是知觉的直接而必然的结果,并举例说明“交换律的成立就是因为观察到图形:::得到2·3=3·2,当点数适当多,这种直接知觉就不行了,但求助于数学归纳法这一抽象的直观,能使我们超越感官知觉所达不到的界限.”[2]一般地,相对于陌生熟悉是直观的,相对于复杂简洁是直观的,相对于特殊普遍是直观的,相对于衍生本原是直观的.关系直观是指以相对具体的、熟悉的、普遍的、本原的模式作为背景,引起对数学某种知识和理论的联想、感悟,从而形成对事物之间逻辑关系的一种比较直接的、形象的推断与理解.事物之间的逻辑关系可分为某个数学知识内在结构关系的分析还原与几个数学知识之间相互关系的同构映射.
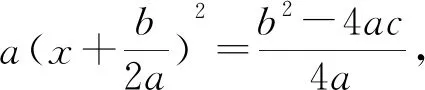
二是相互关系直观.相互关系直观是指把问题的本质结构抽象出来,映射到一个同构或同态的结构上去,形成问题的直观理解或求解方法.项武义教授说:“我当时提出三个几何基本定理:一个是平行四边形定理,一个是勾股定理, 另外一个是相似三角形的定理, 讨论这三个定理的证明后, 就用它们来引进向量运算.基于上述三个几何定理, 强调向量的运算律, 特别是分配律就是上述几何的基本定理的代数形式.”[8]向量的运算及运算律是空间本质的一种至精至简的表达.
关系直观通常是采用形式化的数学语言概括地或近似地表达出来的一种数学结构.
3 直观想象的教学思考
F.克莱因的《高观点下的初等数学》在第二卷的序言中写道,“我想到的是更深入、更广泛的融合……我始终努力想使算术、代数及分析的抽象讨论生动活泼起来,利用图示和作图使内容更容易为个人所接受.”[4]在教学上要充分体现代数与几何的融合,直观与抽象的融合,感性与理性的融合,让学生真正弄懂数学知识的直观含义和直观思路.
3.1 图形直观——直观与抽象的融合
图形直观可以是数与形的转化,形与形的转换,也可以是数与形之间多层面的交叉表达.
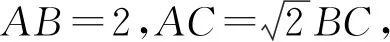
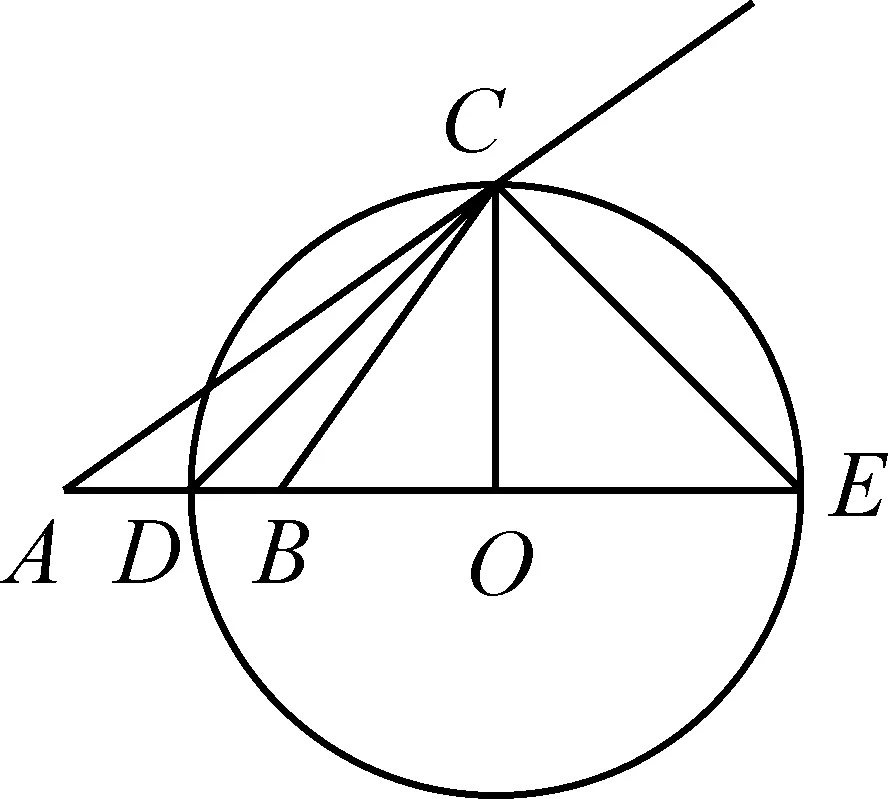
图6
例2设函数f(x)=x2+ax+b在[-1,1]上存在零点,且存在t∈[2,3],使得0≤ta+b≤2,求b的取值范围.如果用代数方法求解或利用f(x)=x2+ax+b的图象讨论a,b应满足的关系,问题解决都会很繁难.注意到式子f(x)=x2+ax+b与 0≤ta+b≤2之间的联系纽带是直线y=ax+b,如图7,函数f(x)=x2+ax+b在[-1,1]上存在零点可以看成是直线与曲线有交点;存在t∈[2,3],使得0≤ta+b≤2即表示直线与矩形区域有交点,这样借助图形直观可以“看”出问题的结果.

图7
例3(清华大学自主招生试题)已知x,y,z都是正数,且满足(x+y+z)xyz=4,求(x+y)2+2(y+z)2+3(z+x)2的最小值.
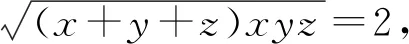

图8
如图8,在AB上取点D,使得AD∶DB=1∶2,
则a2=BC2=CD2+DB2-2CD·BD·cos∠CDB,
2b2=2CA2=2CD2+2AD2-4CD·AD·cos∠CDA,

图形直观可以启迪思路,但构图有难易,分析有繁简,需要合理的选择与变通.直观是抽象的基础,抽象是直观的延伸,两者不可分割,在感知事物的形态与变化过程中相互伴随,不断循环推进.
3.2 模型直观——感性与理性的融合
模型直观以具体的现实情境、生活经验或符号图表等容易理解的具象作为背景,在直观感知的基础上形成对事物关系的理性认识.


从三角运算看,

从物理意义看,如图9,7个力均匀地分布在单位圆上,那么合力必为零,所以在水平方向上分量之和为0.

图9
从向量运算看,因为正多边形的外角和等于360°,所以这7个向量正好可以首尾连接(如图10),那么向量和为0,所以在水平方向上分量之和为0.不同的学科、数学中的不同分支之间的完美统一,让数学知识有了可视化的直观.
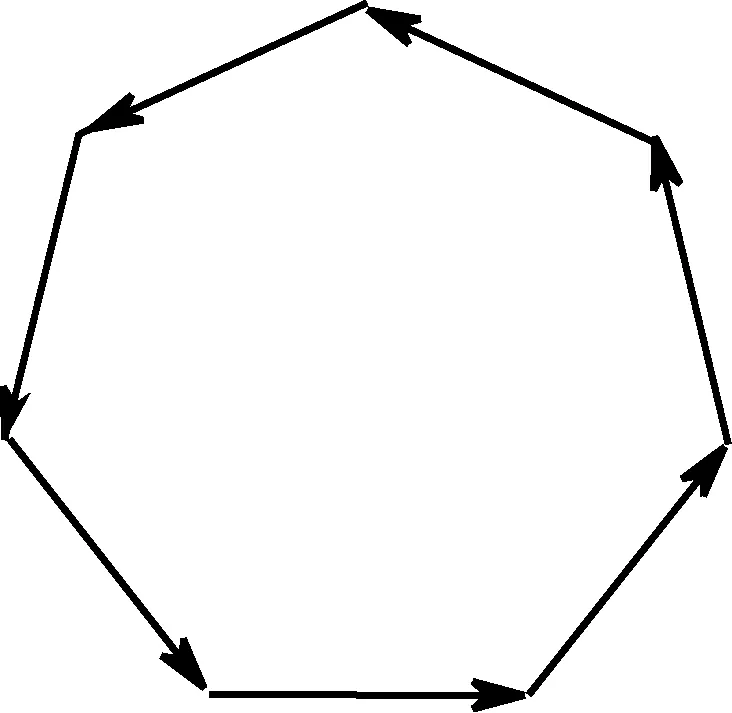
图10
3.3 关系直观——经验与理念的融合
关系直观在于事物间相似的迅速联想,洞察某种可操作或可实现的关系与程序,让思维对象呈现出一种能反映事物间的相互关系、运算性质的整体结构,或者在某种限定条件下的一个局部结构.借助这些逻辑关联的直观化与系统化,得以将局部的直观经验上升到系统的抽象理念,从而丰富认知深度及广度.
例6(清华大学THUSSAT中学生标准学术能力测试题)已知实数a,b,c满足a+b+c=1,a2+b2+c2=1,求a3+b3+c3的最小值.
分析1:a+b=1-c,a2+b2=1-c2,




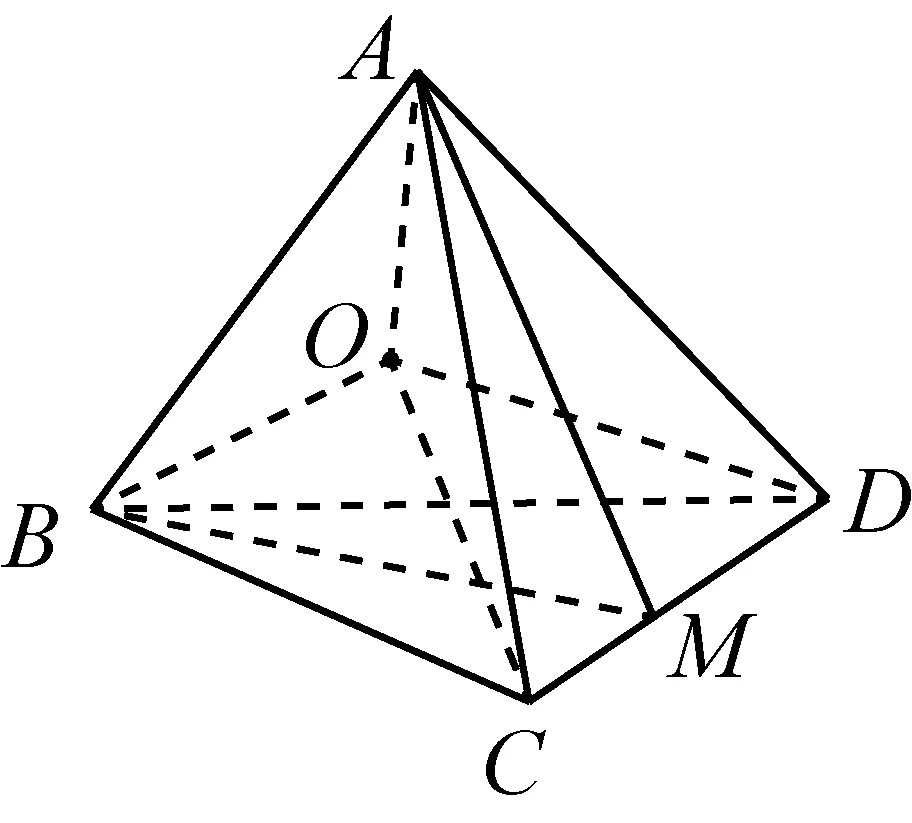
图11

菲尔兹奖获得者康奈尔大学教授威廉瑟斯顿说过,“一旦我看到一些我无法理解的东西,我会去反省和思考,用心灵的眼睛去探求,直到某个时候,视角奇迹般的发生了改变,从迷雾和困惑中出现了形状、秩序与联系.”[9]
4 结束语


图12

