燃料电池车用超高速空压机永磁体结构强度研究

张智明，武赛，潘佳琪，倪玥，章桐

（同济大学 汽车学院，上海 201804）

燃料电池发动机系统研发时工作压力应选择在2×105Pa 附近[1]，相关研究也表明电池性能会随着工作压力的增大而提升，但当压力超过2×105Pa 后，电池性能的提升明显减缓，同时浓差损失开始增加，目前最常用的燃料电池系统工作压力在2 × 105Pa左右[2].燃料电池供气系统中空压机的功耗占整个辅助系统的90%，约为整体输出功率的13%，成本占系统总体的16%[3].空压机作为供气系统的核心部件是燃料电池系统除负载以外最大的附加能耗，其综合性能对整个燃料电池发动机系统的输出功率有着决定性影响.因此研究可靠且低成本的空气供应部件是当前燃料电池发动机研发中的一个重点.

在多种空压机类型中，离心式空压机在功率密度、效率和噪声等方面具有最佳的综合表现，又易于与涡轮相匹配以实现排气能量的回收，被认为是未来发展的主流方向[4].高速永磁电机由于其功率密度高、体积小、动态响应快、结构简单等优点，尤其适用于安装空间有限的车用高速空压机.目前一般选用高速永磁电机作为空压机的驱动电机[5]，其中又以表贴式应用最为广泛.表贴式高速永磁电机转子一般由转轴、永磁体以及保护套三个部件装配而成，电机的输出功率在转矩不变的情况下与转速成正比，在保持空压机体积不变的情况下，要实现高压比、大流量的供气以增加燃料电池的输出功率就必须要提高转子的转速，即朝高速化发展[3].目前超高速转子一般在5 ×104～ 1.5 × 105r/min 以满足30～100 kW 左右燃料电池发动机的空气供应需求.例如搭载于本田Clarity 氢燃料电池汽车中的两级电动涡轮增压空压机的最高转速为1×105r/min，能提供103 W 的最大输出功率.高速永磁电机主要选用第三代稀土永磁合金钕铁硼制造永磁体，该材料有优异的磁性能且可以承受很大的压应力（约为1 000 MPa），但抗拉性能较差，仅有80 MPa.如果未采取有效保护措施，永磁体将无法承受转子高速旋转时所产生的巨大离心力，从而发生断裂破坏[5]，因此转子的结构强度是车用燃料电池空压机转子设计中需要解决的关键问题之一.

最常采用的方法是在永磁体外设置过盈配合护套以施加预压应力与离心拉应力相抵消的方式来保证结构强度，护套的常用材料主要分为非导磁高温合金[6]和碳纤维复合材料[7]两类.张凤阁等[8-9]在两项研究中指出碳纤维护套在强度要求相同时所需的厚度更小，且在散热条件相同时的温升更低，有着出色的综合性能.吴震宇等[10]的研究也表明碳纤维护套的机械强度和电磁性能优于其他材料，动力学特性也更佳.张超等[11]研究了转轴材料热膨胀系数在高温时对永磁体应力巨大的影响，指出了热态强度校核的必要性；并在另一项研究中发现合金护套和碳纤维护套的等效应力均随温升线性增大，而碳纤维护套的增长率更高[12].马振杰[13]分别研究了转速和温升对转子结构强度的影响，结果表明温升对应力的影响远高于转速，是最需要重视的影响因素.

从保证空压机正常工作、结构强度可靠性和运行稳定性的角度出发，对高速空压机转子各部件应力及其分布的研究是十分必要的.本文分别计算了转子在静止和额定工作转速两种工况时不同半径位置的应力，校验了永磁体和护套所受应力的极值是否在安全范围内，以达成设计的强度要求.由于永磁体抗压能力很强但抗拉能力较差，永磁体和保护套之间可以采用过盈量较大的配合，使永磁体在静态就承受一定的预压应力[14]，以部分或完全抵消高速离心力造成的拉应力影响.除上述研究中提及的过盈量大小和护套材料外，离心力与转子转速的平方成正比，与转子的结构强度有着密切关联，因此本文也将在其后的章节中分析该因素的影响.

1 过盈量的确定

永磁体和护套之间可以采用过盈量较大的配合，使永磁体在静态时能承受一定的预压应力，过盈量的大小可通过解析计算来确定.根据材料力学，当电机转子的护套与永磁体间存在过盈量时，其配合表面会产生使护套内径向外膨胀、永磁体外径向内收缩的压应力.在过盈量初值的理论计算方法中，忽略护套和永磁体在轴向的长度和应变，把结构视为两个无限长厚壁圆筒间的过盈配合，并采用拉美方程进行分析.转子的永磁体与护套结构尺寸如图1所示.

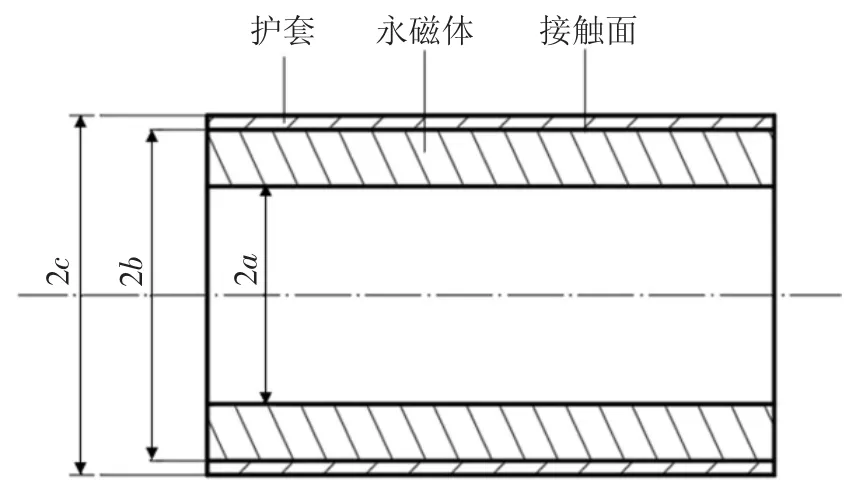
图1 转子的永磁体与护套结构尺寸Fig.1 Size of permanent magnet and sleeve

图1 中，a 为永磁体内半径，b 为护套的内半径，也是永磁体的外半径，c 为护套外半径.

该燃料电池空压机电机的设计额定转速为8×104r/min，其转子的护套和永磁体的尺寸参数分别为a=11.5 mm，b=17.5 mm，c=19.0 mm，长度l=0.06 m.护套和永磁体的材料属性如表1 所示.

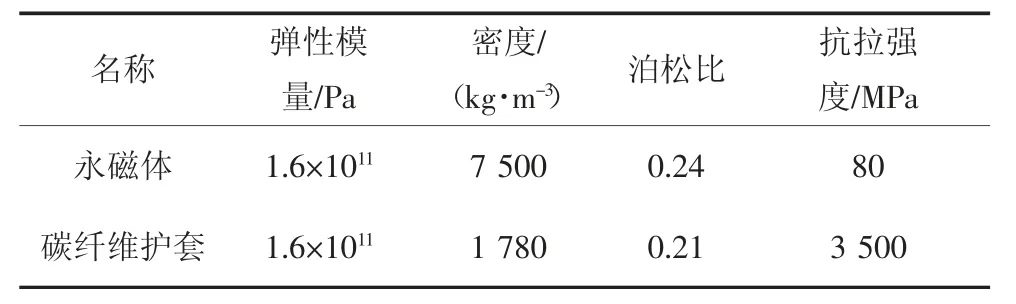
表1 转子护套和永磁体的材料属性Tab.1 Material properties of sleeve and permanent magnet

1.1 过盈量的计算方法分析

工程材料通常可分为塑性材料和脆性材料两大类.前者以屈服为主要失效形式，极限应力为屈服极限；后者的主要失效形式是断裂，以强度极限为极限应力.钕铁硼永磁体为脆性材料，应采用最大拉应力理论和最大伸长线应变理论进行校核；碳纤维护套属于塑性材料，应采用最大剪应力理论和形状改变比能理论进行校核.对永磁体主要分析径向和切向应力，对护套主要分析等效应力[15].

对于绕轴线旋转的圆柱体，其应力分量σθ、σr、σz依次为切向、径向和轴向这3 个方向的主应力.在高速永磁电机的转子护套和永磁体的过盈量的计算中，应该首先考虑满足的条件是永磁体的切向应力σθ小于其抗拉强度，在σθ满足条件的情况下求出过盈配合量的值，然后根据过盈量值进行高速旋转时永磁体内应力的计算和分析.转子护套中的等效应力可在永磁体强度校核完成后进行验证.护套与永磁体的理论法计算流程如图2 所示[16-17].

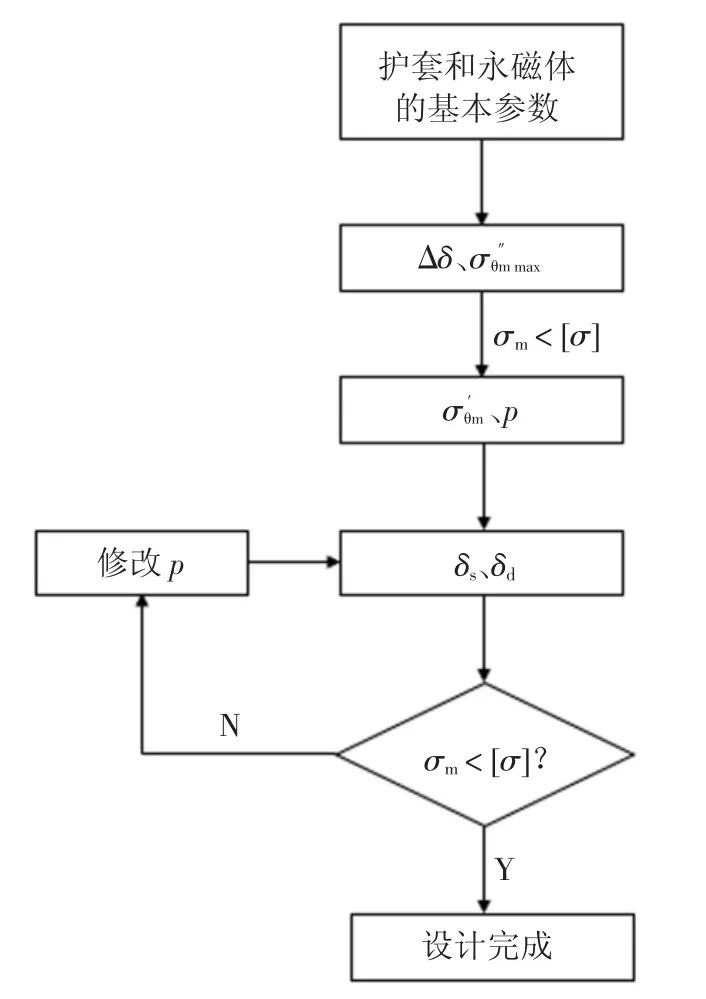
图2 护套与永磁体间过盈量的理论法计算流程Fig.2 Theoretical method for calculating the interference between the sleeve and permanent magnet

图2 中，Δδ 为过盈量的减少量，δs为静态过盈量，δd为动态过盈量，和为永磁体静态和动态时的切向应力，p 为接触面压应力，σm为切向应力极值，[σ]为强度极限.

1.2 过盈量的计算结果

根据丁鸿昌等[17]提出的理论计算方法、表1 和图2，可以得出过盈配合面半径r=b 处转子护套的径向位移分量=3.492 48×10-3mm；永磁体的径向位移分量=8.790 26×10-3mm；以及两者间的差值，即过盈量的减小量Δδ=-5.3×10-3mm.

然后计算半径r=a 处旋转的永磁体的最大切向应力分量，其值为=145.54 MPa.

由于永磁体抗拉强度[σ]为80 MPa，要保证永磁体在高速工况时不损坏就需要满足σθ≤[σ]/k.其中k 为安全系数，取值1.2，r=a 处的静态切向应力分量=-78.87 MPa，取整-80 MPa.

将静态过盈量与过盈量的减少量相减计算动态过盈量δd=3.53×10-2mm.再由δd计算得到对应的动态过盈压力pd=27.52 MPa.

综上，解析计算所得的结果为：护套与永磁体的静态过盈量为0.03 mm，静态过盈装配压力约为23.39 MPa，而动态过盈压力会提升至27.52 MPa.根据初步计算结果可以求出高速旋转时永磁体内不同半径位置的应力，在工作转速时永磁体内径向应力为-27.52～ 0 MPa，永磁体内切向应力为15.92～48.66 MPa.

2 转子强度有限元分析

2.1 建立有限元接触力学模型

永磁体和护套的结构简图如图1 所示，永磁体和护套的结构均为空心圆柱体，因此可作为轴对称问题使用弹性力学中的厚壁圆筒理论进行解析法计算，但是在采用解析法计算时忽略了永磁体和护套长度这一属性，未考虑两者的轴向应变，简化该模型就会导致一定的误差.本节应用ANSYS 软件进行有限元法分析，有限元模型包含了结构的长度，考虑永磁体和护套在轴向的应变，因此应力计算结果会更加精确.

永磁体与护套的尺寸参数及材料属性都与解析法计算时相同，另设两者的长度均为60 mm.建立的y 轴对称模型如图3 所示.

图3 二维轴对称模型图Fig.3 Two-dimensional axisymmetric model

永磁体和护套选用PLANE 183 单元来建模，此次建模为二维轴对称模型，在定义单元时需要将Element behavior 设置为Axisymmetric.而永磁体和护套间的过盈配合可按照有限元的接触理论设置一对线-线接触单元来模拟，通常是成对使用CONTA 172单元和TARGE 169 单元.故转子护套和永磁体之间的过盈配合是通过在配合面对应的线上生成CONTA 172 单元和TARGE 169 单元来定义的，该方法可以较为准确地模拟轴对称模型中的过盈配合[18].设置过盈量值为前文中理论计算所得的0.03 mm，分配各截面对应的材料属性并选用映射网格对模型进行划分.

划分网格之后，对整个模型建立约束.先约束永磁体内表面和护套外表面上所有节点在径向上的位移，再固定两边中间节点在轴向上的位移，设置约束后的模型如图4 所示.最后设置转子绕y 轴的转速为8×104r/min

图4 二维模型的约束Fig.4 Constraint of two-dimensional axisymmetric model

2.2 ANSYS 仿真结果分析

为了分析转子在静态和工作转速工况下永磁体和护套内部应力以及接触面接触压力的变化，设置过盈量为0.03 mm，对转速为8×104r/min 和0 r/min时的动态和静态工况进行仿真.所得各应力云图如图5 和图6 所示，整理数据结果汇总于表2 中.在转速为8×104r/min 时，从接触应力以及永磁体径向应力和切向应力的数值可知，仿真结果与前文中解析法计算所得到的结果相近，相对误差不大于2.5%，证明了该有限元仿真模型和计算方法的正确性.在转子以8 × 104r/min 的高转速工作时，永磁体中的最大切向应力为48.2 MPa，最大径向应力为1.5 MPa，均远低于永磁体的抗拉强度80 MPa，故永磁体不会出现破坏；护套中的最大等效应力为395 MPa，而制造护套的碳纤维材料其抗拉强度一般超过3 500 MPa，所以护套在工作时也能满足其强度要求.

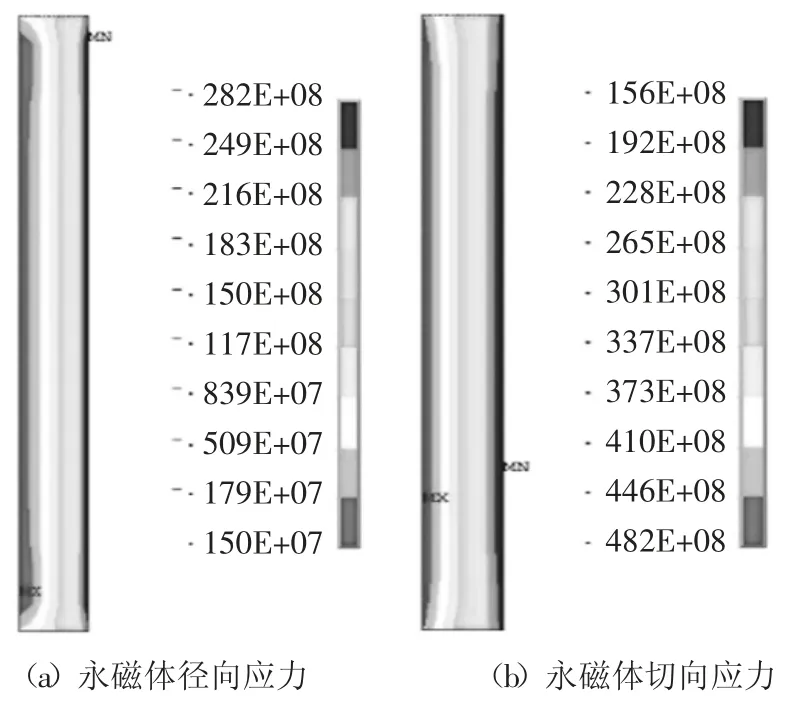
图5 8×104 r/min 时永磁体及护套应力云图（单位：Pa）Fig.5 Stress contour of sleeve and permanent magnets at 8×104 r/min（unit：Pa）

图6 0 r/min 时永磁体及护套应力云图（单位：Pa）Fig.6 Stress contour of sleeve and permanent magnets at 0 r/min（unit：Pa）

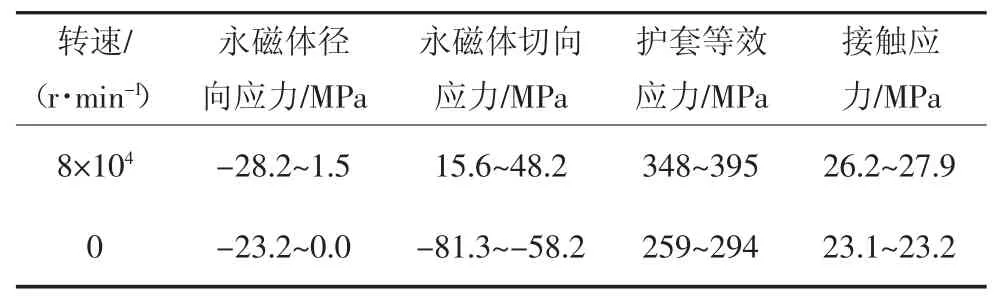
表2 8×104 r/min 和0 r/min 下永磁体及护套应力仿真结果对比Tab.2 Comparison of stress simulation results of sleeve and permanent magnets at 8×104 r/min and 0 r/min

对比0 r/min 和8×104r/min 转速下两种工况的应力可以看出：在转子高速旋转时接触面上的最大接触应力由23.2 MPa 提升至27.9 MPa，接触应力增大；最大径向应力由0.0 MPa 变为1.5 MPa，最大切向应力由-58.2 MPa 变为48.2 MPa，切向应力和径向应力也同样增大，切向应力由压应力变为了拉应力.根据前文理论计算时所得，在高速旋转时永磁体与其碳纤维护套间的过盈量较静态时有所增加，这也是导致接触面上接触压力增大的原因.虽然接触面上接触压力的增大有助于维持过盈配合的状态，即有利于使永磁体受压应力的作用，但仍然无法与高速离心力引起的拉应力相抵消，最终永磁体在切向方向从原来的受压转变为承受一定的拉应力.鉴于永磁体的抗拉强度很小，所以设置的过盈量既不宜过小也不宜过大，存在一个适中的取值范围.

一般来说，当转子高速旋转受到很大离心力时，接触面应该有分离的趋势，会引起接触面上的接触应力有所减小，但表2 中的数据显示永磁体与其碳纤维护套间的接触应力反而有所增加，这是由于碳纤维材料的低密度使得护套所受的离心力较小，而高弹性模量又使其抗变形能力较强.由此可以看出，护套材料对护套和永磁体之间的接触有很大影响，进而对永磁体的强度造成影响.除了护套的材料之外，在转子结构不改变的情况下，转子转速、装配过盈量以及温升等参数影响还需要进一步分析.

2.3 永磁体强度的关键因素分析

分别设置转速为6 × 104r/min，过盈量为0.05 mm，护套材料为合金钢，重新进行仿真分析.钢护套和碳纤维护套的材料属性如表3 所示，仿真结果如表4 所示.

表3 护套的材料属性Tab.3 Material properties of sleeve

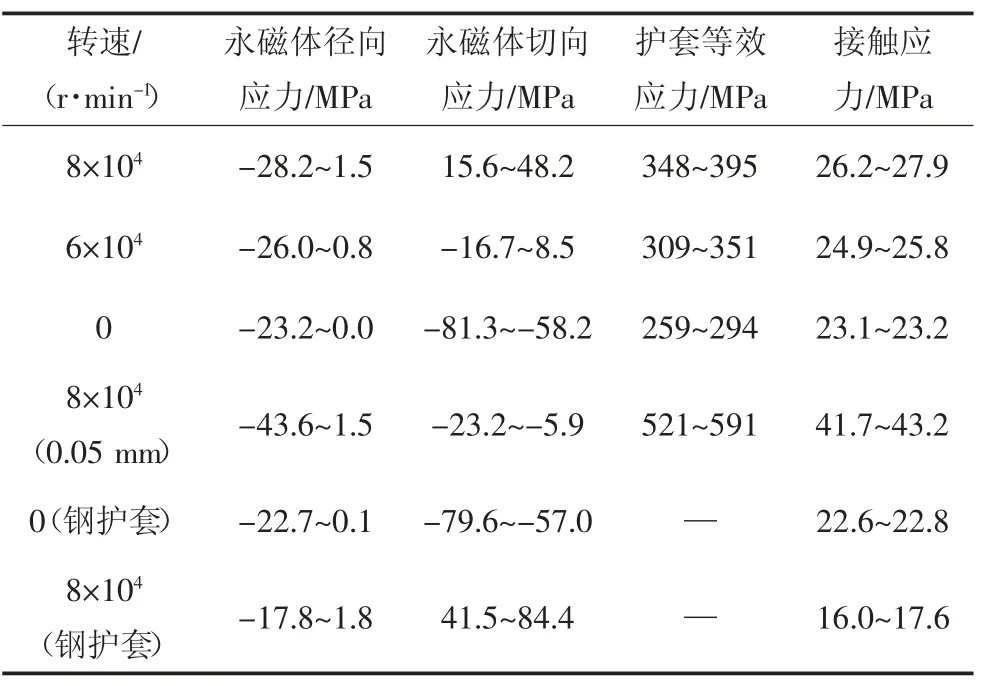
表4 不同转速及过盈量下的结构强度Tab.4 Structural strength at different speeds and interference

对比转速为6 × 104r/min 与8 × 104r/min 两种工况下的应力可以发现，永磁体内的最大切向应力、最大径向应力，护套内的等效应力以及接触面的接触应力均随转速的降低而有所减小，有利于永磁体和护套的保护，使其远离各材料的强度极限.但考虑到空压机的工作方式是电机驱动转子高速旋转带动叶轮对外做功，将自然空气压缩成高压空气并提供给燃料电池系统，所以，对于空压机，转速对外的输出性能有着至关重要的影响.由上可知，降低转速，理论上的确是降低永磁体所受拉应力的有效方式，但在实际应用中会降低输出功率，故不宜采用.

在转速为8×104r/min，对比过盈量分别为0.03 mm 和0.05 mm 两种情况下的应力可以看到，随着过盈量的增加，接触面上的最大接触应力也随之增加，由27.9 MPa 增加到43.2 MPa，由此所能提供的预压应力也就增加了.在高速旋转时，永磁体的最大切向应力由原来的48.2 MPa 拉应力转变为5.93 MPa 压应力，即在转速为8×104r/min 时，永磁体在切向方向依然承受的是压应力；而在径向方向虽然永磁体的最大径向应力基本保持不变，但永磁体在整体上承受了更大的压应力，这对于保护永磁体来说是有利的.护套的最大等效应力也随着过盈量的增加而呈现显著提升，从原来的395 MPa 增长为591 MPa，提高约49.62%.

虽然护套的最大等效应力依然没有超过它的抗拉强度，但可以看出护套的最大等效应力会随着过盈量的增加而迅速增大.由此可知，虽然增加过盈量对保护永磁体免受拉应力的影响很有帮助，但考虑到过盈量的增加会同时增加护套的最大等效应力，而且太大的过盈量也会使装配流程更为困难，所以一味地增加过盈量的值也是不可取的.对于过盈量，仍然需要通过适当的计算来选取最合适的值，这样才能使整个转子最安全有效地工作.

对比0 r/min 与8×104r/min 两种工况时的应力可以看出，在使用钢护套且转速为8×104r/min 时，接触面上的接触应力要小于0 r/min 时的情况，即永磁体和护套间的过盈配合有分离的趋势，造成这个结果的原因是过盈量的减小，其值是由旋转转子护套和永磁体在径向位移量的差值所决定的.在永磁体位移量相同的情况下，护套的位移量就会决定过盈量是减小还是增大，即接触面间是有分离趋势还是压紧趋势.当护套的位移量大于永磁体的位移量时，接触面就会有分离的趋势，反之则有压紧的趋势.

从护套位移量的计算式中可以看到，泊松比对位移量的影响相对较小，护套材料的密度越大、弹性模量越小，护套的径向位移量也就越大.钢护套的弹性模量值与碳纤维护套的弹性模量值很接近，而密度却远大于碳纤维护套，因此在护套材料为钢时，在离心力作用下的位移量更大，也就造成了接触面有分离的趋势，接触面上的接触应力也相应减小.

此外，由于钢护套和碳纤维护套的弹性模量相差不大，因此在使用钢护套时，永磁体的预压应力比使用碳纤维护套时只是略有减小.对比转速同为8×104r/min 时钢护套和碳纤维护套下永磁体的应力可以看出，由于在使用钢护套时接触面间有分离的趋势，加之转子高速旋转时产生的巨大离心力作用，才会造成永磁体的切向应力与使用碳纤维护套时的巨大差别；永磁体切向的拉应力大幅增加，甚至已经超过了永磁体的抗拉极限，导致永磁体出现强度破坏.

由此可见，在同等条件下，只要改变护套的材料就会对高速旋转时的永磁体内部应力带来显著的变化.正因为护套材料的影响如此之大，所以在选择护套材料后必须重新进行校核，以免无法在高速运转时有效保护永磁体.理论上，选择密度更小、弹性模量更大的材料更有利于保护永磁体免受拉应力的影响，但在实际选择护套材料时还需考虑实际的情况选择最合适的护套.

2.4 温升对永磁体强度的影响

除了过盈量、转速和护套材料这三项因素外，温升也会对转子强度产生影响[19].转子在高速运行一段时间后，机械和电磁损耗均会使转子的温度升高.由于护套和永磁体材料热膨胀系数不同，接触面间的过盈量有所减小，从而导致接触压力的减小，造成护套的等效应力和永磁体的拉应力均相应增大，最终可能由压应力转变为拉应力，甚至拉应力的极值超过永磁体的抗拉强度.因此，在设置过盈量时，需考虑是否适当增加过盈量的大小以抵消温度上升对过盈量和永磁体强度带来的影响.钕铁硼的热膨胀系数为6.5 × 10-6℃-1，碳纤维的热膨胀系数为8.8 ×10-6℃-1，钢的热膨胀系数为10.5×10-6℃-1.对2.1节中的模型施加不同的温度载荷，并设置参考温度为20 ℃，过盈量为0.03 mm，转速为8×104r/min，护套材料分别选用碳纤维和钢.部分仿真结果如图7和图8 所示，数据汇总于表5 中.将表5 中永磁体最大拉应力和温升的关系进行数值拟合，所得关系曲线如图9 所示.

图7 8×104 r/min、100 ℃时护套等效应力和永磁体拉应力（碳纤维护套，单位：Pa）Fig.7 Equivalent stress of sleeve and tensile stress of permanent magnets at 8×104 r/min and 100 ℃（carbon fiber sleeve，unit：Pa）

图8 8×104 r/min、100 ℃时护套等效应力和永磁体拉应力（钢护套，单位：Pa）Fig.8 Equivalent stress of sleeve and tensile stress of permanent magnets at 8×104 r/min and 100 ℃（steel sleeve，unit：Pa）

表5 温升对各项应力的影响Tab.5 Effect of temperature rise on stress

由表5 可知，随着温升的提高，护套和永磁体间的接触应力逐渐降低，这表明了装配过盈量会因热变形而减小.由于过盈配合对永磁体的保护作用削弱，永磁体所受的最大拉应力逐渐增大.温升100 ℃时，永磁体搭配碳纤维护套和钢护套所受的最大拉应力相比室温时分别提升了30.0%和39.1%.尤其是钢护套保护的永磁体在温度升高20 ℃时就已超过了材料的强度极限.这是由于钢材料的热膨胀系数高于碳纤维和永磁体，所以装配过盈量随温升的减小会更显著.温升从0 ℃升至100 ℃时，改用碳纤维护套使永磁体应力的降幅从42.1%增至45.9%.

温升所引起的装配过盈量减小值同样可使用弹性力学理论计算：

式中：αst为护套的热膨胀系数（℃-1）；αpm为永磁体的热膨胀系数（℃-1）；r 为配合面半径（m）；ΔT 为温度升高量（℃）.

由式（1）可以计算出钢护套由温升导致的过盈量减小量为7×10-3mm，相比碳纤维护套增长约73.91%.因此，在护套材料的选取上应尽量选择热膨胀系数较低且与永磁体相近的材料，这样可以有效抑制温升对过盈量的影响，从而提升转子的最高工作温度.

从图9 的关系曲线可以看出，两种护套材料的永磁体最大拉应力均随温升呈近似线性增大，两者间的数值关系为：

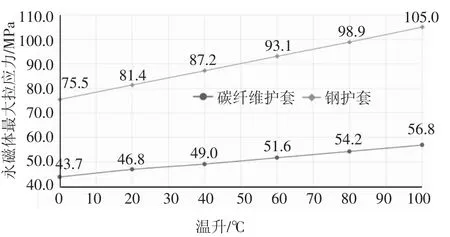
图9 永磁体最大拉应力-温升关系曲线Fig.9 Max tensile stress of permanent magnets and temperature rise relation curves

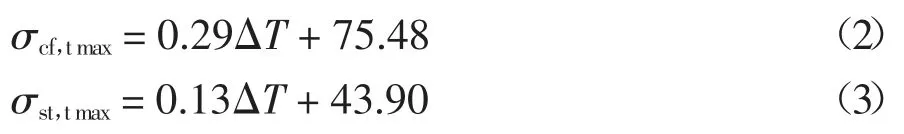
式中：σcf，tmax和σst，tmax为搭配碳纤维护套和钢护套时的永磁体最大拉应力（MPa）.

从式（2）和式（3）中ΔT 的斜率可以看出，搭配钢护套时拉应力极值随温度的增长率是碳纤维护套时的2.23 倍，这表明在使用钢护套时结构强度受温升的影响更大.通过此数值关系也可以推算出在安全系数为1.2 时，安装碳纤维护套的转子最高工作温度可达176.5 ℃，远高于电机转子的正常工作温度.结果表明碳纤维护套材料在高温工况时具有显著优势，不仅在工作温度范围内无需进一步增大过盈量来加强保护作用，而且受热变形的影响也更小.

3 结束语

在对驱动燃料电池车用空压机所使用的高速永磁电机转子分别进行解析法和有限元法强度计算后，可得出以下主要结论：

1）过盈量的初值可通过护套与永磁体间的接触压力确定，接触应力的最小值为永磁体抗拉强度与安全系数相除所得；过盈量的减小量与转子转速的平方成正比，且受护套材料密度和弹性模量的影响.

2）解析计算方法和有限元模型仿真方法的计算结果十分相符，各应力的相对误差小于2.5%.这是由于解析计算方法忽略了轴向应变的影响，而在有限元分析中考虑了轴向应变的影响.鉴于2 种方法计算的相对误差较小，故可认为解析计算方法具有足够的计算精度.

3）转子转速、过盈量大小以及护套材料等都是永磁体和护套结构强度的重要影响因素，降低转速或增加过盈量都能有效减小永磁体所受拉应力.分析结果表明，选用密度更小、弹性模量更大的护套材料可有助于抑制工作转速时实际过盈量的减小.但在实际选择护套材料时还需综合考虑加工工艺、制造成本和装配方式等多方面的因素.

4）温升对过盈量的减小有显著影响，会使接触面压力降低，永磁体所受拉应力的极值随温升近似线性增大.因此需要对转子的热态工况进行计算以验证是否应适当增加静态过盈量以抵消热变形的影响.此外，选择热膨胀系数与永磁体相近的护套材料更有助于抑制温升对转子强度的削弱作用.结果表明碳纤维护套在高温工况时对永磁体的保护效果优于钢护套.