一种面向热设计的反馈-模糊推理全局算法

雷飞，张天昊

（湖南大学汽车车身先进设计制造国家重点实验室，湖南长沙 410082）

电动汽车电机控制器内部的集成化程度越来越高，控制器内元器件的发热量不断增加.在有限的物理空间内，多合一控制器中大功率元件的热通量可达200～ 300 W/cm2.过高的温度会直接损坏元器件，热设计和热管理成为集成控制器设计的关键环节[1].

热设计问题通常是已知目标温度来求解相关设计参数，本质上属于已知目标温度求解几何边界的传热学反问题[2].通常基于传热系统的局部测量温度信息，求解系统的热流密度、热源参数、热物理参数和几何参数等难以测量的未知参数的问题.在控制器热设计问题中，由于大量电子电器元件高度集成导致其传热规律复杂，难以得到传热学规律的定性描述.复杂的传热规律是该问题的典型特点之一.

不适定性是传热学反问题的另一特点.这种不适定性是指该问题在Hadamard 意义下解的唯一性、存在性和稳定性不能同时得到满足[3].一方面，由于输入信息不全面，反问题的解可能不存在或不唯一；另一方面，由于输入信息存在偏差，输入信息的误差在反问题的求解过程中会被放大，从而导致反问题的解往往存在不稳定性.反问题的不适定性为求解带来了较大挑战.

传热学反问题的求解方法可分为非迭代法和迭代法.非迭代法依据已知的测点信息和待求解量之间的数学关系，直接通过已知量计算待反演参数，无需反复计算正问题以修正计算结果，可实现较高的计算速度.吴国鹏等[4]基于最小二乘法和误差函数反演了功能梯度材料热源发热功率；Yu 等[5]将最小二乘法和边界元法相结合提高算法的抗不适定性并对锅炉内壁的几何边界进行了反演；Yu 等[6]利用边界元法分别在稳态下和瞬态下对炉内壁的边界条件进行识别.对于复杂传热学问题，由于已知条件和待求解量之间的数学关系建立存在困难，该类方法应用有限，同时存在不适定性问题.

迭代法可分为梯度法和非梯度法，其中经典的梯度法有最速下降法（Steepest Descent Method，SDM）、共轭梯度法（Conjugate Gradient Method，CGM）、Levenberg-Marquardt 法（L-M）等.Huang 等[7]通过SDM 成功反演了翅片换热器的换热系数；Yang等[8]采用改进的L-M 法估算了传热学反问题中的导热系数；Xiong 等[9]应用CGM 反求了二维传热系统中的热流量；王堃等[10]用正则化CGM 估计了二维稳态传热边界温度分布.

梯度法可以解决部分传热学反问题，但当传热规律较为复杂时会陷入局部最优，且问题的可微性不能保证.此外，如果测量信息不完整或存在测量误差，梯度法的求解结果可能出现恶化[11].

非梯度法具有良好的抗不适定性能力和全局搜索能力，但计算量较大.这类方法有遗传算法、蚁群算法等，近年来随着计算技术的发展而得到较广泛应用.Lee 等人[12]利用粒子群优化方法估计介质的辐射特性；Liu[13]用一种改进的遗传算法估算瞬态传热系统的平板热源功率；Parwani[14]等人利用差分进化算法估算了传热系统中热源的发热功率和位置.

模糊推理是20 世纪60 年代Zadeh 提出的一种启发式算法[15].它是在模糊集合论基础上对人脑的决策和判断做定量研究的一种不确定推理方法.该算法只需从单一起始点开始计算，相对于蚁群算法、遗传算法等需要多个初始点的非梯度类算法而言计算成本较低，具有良好的抗不适定性，能有效抵抗输入信息的干扰[16].此外，模糊推理算法可以有效利用不精确和不完整的信息[17].这些特点在解决包括传热学反问题在内的不适定问题时具备优势.Wang 等[18]提出了分散模糊推理算法用来求解热传导反问题中的几何参数；Krzywanski 等[19]利用模糊推理算法预测了大型循环流床的导热系数；Chen 等[20]提出一种具有目标跟踪能力和降噪性能的智能加权模糊推理算法，并将其应用于空心复合管的热传导几何参数反演问题中；姜曙等[21]利用分散模糊推理对圆筒热传导问题的几何边界进行了反演.在以上传热规律明确的问题中，模糊推理方法均取得了较好的结果.

但是，常规模糊推理方法中模糊规则的制定对传热学规律的认知依赖程度较高，在求解传热学规律未知或其定性描述为非单调的传热学反问题时，常规模糊推理算法会由于无法制定模糊规则而失效.

本文针对传热学规律未知或非单调的传热学反问题提出一种改进的模糊推理算法，该算法以变论域模糊推理方法为基础，结合反馈算法和模拟退火算法的优势，不仅降低对初始论域依赖性，同时降低模糊规则对传热规律认知的依赖性.使用该方法对电动汽车集成控制器的风冷散热器进行设计，并讨论初始值和测量误差对该方法的影响.

1 算法描述

反馈-模糊推理全局算法由模糊推理单元，反馈单元和模拟退火单元组成.

若传热学反问题的传热规律较复杂或未知，则可以通过模拟退火单元防止结果陷入局部最优.记uk（i）为模糊推理单元第i 次迭代的输出，n（i）为待求解量第i 次迭代的计算结果，Tcal（i）为第i 次迭代的计算温度，迭代结束条件为≤ε，ε 为收敛条件.算法的流程如图1 所示.

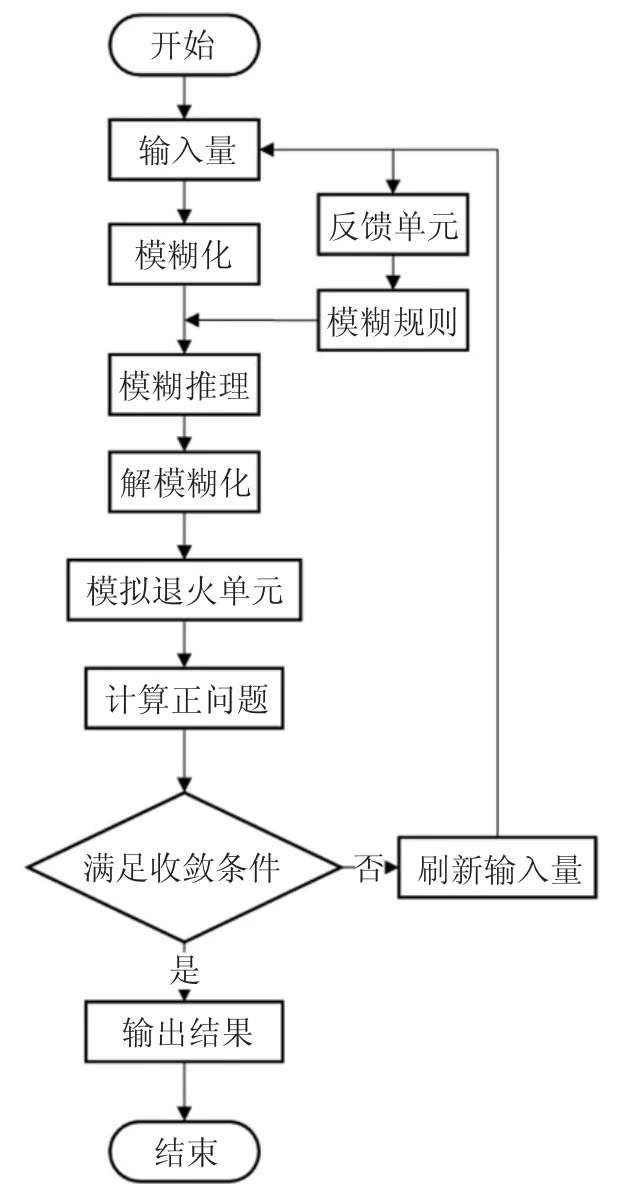
图1 反馈-模糊推理全局算法流程图Fig.1 Algorithm flow chart of the feedback-fuzzy inference global method

2 问题描述

图2 为某电动汽车集成控制器的简化几何模型，该控制器箱体外形尺寸为388 mm×288 mm×124 mm，芯片为方形均匀体热源，为模拟芯片封装，在元件外部增加聚苯硫醚（Polyphenylene sulfide，PPS）材料外罩；用各向异性材料模拟印制电路板（Printed Circuit Board，PCB）；IGBT 为导热性良好的均匀方形体热源；为模拟IGBT 的水冷，将箱体底部设为333 K 恒温边界，其余的面设为298 K 恒温边界；箱体材料及翅片散热器材料选用铝材，各材料物性参数见表1；系统内热源及其发热功率见表2；风冷散热器尺寸结构如图3 所示.

图3 风冷散热器几何结构示意图Fig.3 Illustration of geometric structure for the air-cooled radiator

表1 材料物性参数Tab.1 Physical parameters of materials

表2 热源及其发热功率Tab.2 The heat sources and heating power

未安装风冷散热器时1、2、3 号芯片温度分别为392、411、389 K，其中2 号芯片的温度超过了设计要求的393 K，故对安装在PCB 下方风冷散热器的翅片数量进行设计，使2 号芯片温度降至378 K.该问题本质上属于已知测点温度求解几何边界的传热学几何反问题，即求解翅片数量n 使得≤ε，其中Tmea为2 号芯片的目标温度，Tcal为每次迭代过程的计算温度，ε 为迭代停止阈值或收敛条件，由于该问题中的目标温度精度要求为1 K，故在此ε 取值为1.

该传热系统中同时存在热传导、热对流、热辐射，假定在控制器内的空气为理想气体，其流动为三维湍流流动，且忽略辐射换热，则正问题的控制方程如下.

热传导方程：

热对流质量守恒方程：

热对流动量守恒方程：

热对流能量守恒方程：

式中：V 为流体速度；T 为流体温度；F 为体积力；P为压力；τ 为时间；ρ、λ、η 和cp分别为流体的密度、热导率、动力黏度和比热容.

由式（1）～式（4）可知，由于该问题为热传导和热对流共存的复合传热问题，传热规律较为复杂.

3 反馈-模糊推理全局算法

3.1 模糊推理单元

模糊推理是以模糊集合理论为基础，结合计算机语言规则和先验知识，模仿人类思维进行判决的不确定推理方法，其本质是将一个给定输入空间通过模糊逻辑映射到一个特定的输出空间的计算过程.

模糊推理算法的具体模块有模糊化、模糊规则的制定、模糊推理和解模糊化，如图4 所示.

图4 模糊推理单元和流程Fig.4 Fuzzy inference units and its process

3.1.1 模糊化

上述可变输出域可以保证输出域的大小与输入量e 正相关，从而在e 较大时提高迭代速度，在e 较小时提高推理精度并且保证推理的稳定性，减少初始域对输出的影响.

输入变量e 和输出变量uk的论域分别划分为4个模糊等级，对应的语言值为零（ZO）、正小（PS）、正中（PM）、正大（PB）.采用三角形隶属度函数，此时输入论域、输出论域及其对应的隶属度函数分别如图5和图6 所示.

图5 输入论域及其对应的隶属度函数Fig.5 The membership function for the fuzzy set of input value

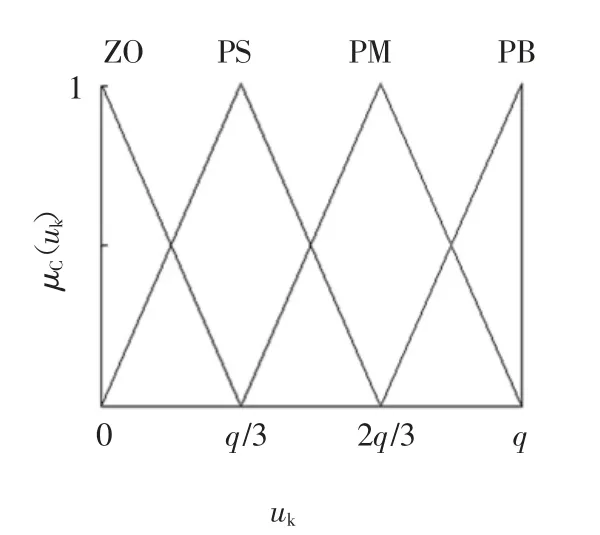
图6 输出论域及其对应的隶属度函数Fig.6 The membership function for the fuzzy set of output value

3.1.2 模糊规则的制定

一般来说，带翅片的风冷散热器的传热规律可定性描述为：当底板面积一定，翅片数量在一定数量范围内时，散热效果随翅片数量增加而增强；超过某一数量范围，增加散热翅片时，散热效果会因风阻而降低.理论上，这是一个单极值问题，但由于本传热系统中的众多其他热源会对翅片散热效果产生影响，因此传热规律不能简单地做定性描述.这种情况下常规模糊推理会因模糊规则不明确而失效.本文提出的反馈-模糊推理全局算法中模糊规则仅用来确定输出值的大小，此时模糊规则的制定仅影响计算效率.不考虑传热规律的模糊规则如下：

1）If e is PB then ukis PB，

2）If e is PM then ukis PM，

3）If e is PS then ukis PS，

4）If e is ZO then ukis ZO

3.1.3 模糊推理和解模糊化

本文采用Mamdani 法作为模糊推理方法，定义μA（e）、μB（μk）分别为输入变量和输出变量对应模糊集的隶属度函数，μC（uk）为模糊推理结果，计算过程可表示为：

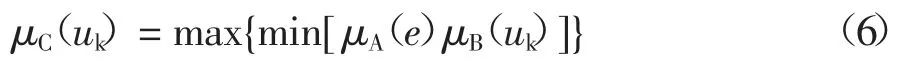
解模糊化方法采用重心法，计算公式为：

3.2 反馈单元

根据反馈的基本思想，每次迭代的计算结果都将传递给该单元进行判断，若优于当前结果，则采纳该结果；若劣于当前结果，则重新选取补偿方向.利用反馈单元对补偿量符号进行判断的代码如下，其中r 为随机数.

3.3 模拟退火单元

模拟退火算法是一种基于蒙特卡罗迭代求解策略的随机优化方法.该算法模拟了固体退火规律，结合温度下降过程中的概率跳跃，随机搜索目标函数的全局最优解.当问题的传热学规律定性描述为单极值问题时可不使用此单元.由于本研究中反问题的传热学规律未知，为避免陷入局部最优，故在反馈单元的基础上加入模拟退火单元进行全局求解.

设置当前退火温度为T，退火初始温度T2=90 ℃，退火结束温度T3=89.9 ℃，降温方式采用等比例降温，比例系数j 为0.999，结果接受准则为：

当Tcal（i）-Tcal（i-1）＜0 时，接受当前结果；当Tcal（i）-Tcal（i-1）≥0 时，如果rand ＜e（-（Tcal（i）-Tmea（i））/T），接受结果，否则不接受.

3.4 计算过程

Step1设置模糊推理的输入量e 与输入论域，输出量uk与输出论域，初始化迭代次数i=1；

Step2进入模糊推理模块求解uk（i），令n（i+1）=n（i）+uk（i）；

Step3根据n（i+1）计算正问题，得到Tcal（i+1）和e（i+1）；

Step4判断e（i+1）≤1 或T ＜T3是否满足，如果满足，终止迭代并输出n（i+1），否则i=i+1，迭代继续；

Step5重复Step2—Step4，当i ≥2 时进入反馈单元和模拟退火单元；

Step6T2=T2×j；

Step7重复Step4；

Step8重复Step2—Step7.

4 计算结果及讨论

4.1 计算结果及验证

当初始翅片数为25 时，使用反馈-模糊推理全局算法和模拟退火算法计算翅片数和目标芯片温度的迭代结果分别如图7 和图8 所示.在相同的输入、输出论域条件下，使用常规模糊推理计算翅片数和目标芯片温度的迭代结果分别如图9 和图10 所示.为了验证算法的准确性，本文通过仿真计算了采用不同翅片数时芯片温度的情况，如图11 所示.

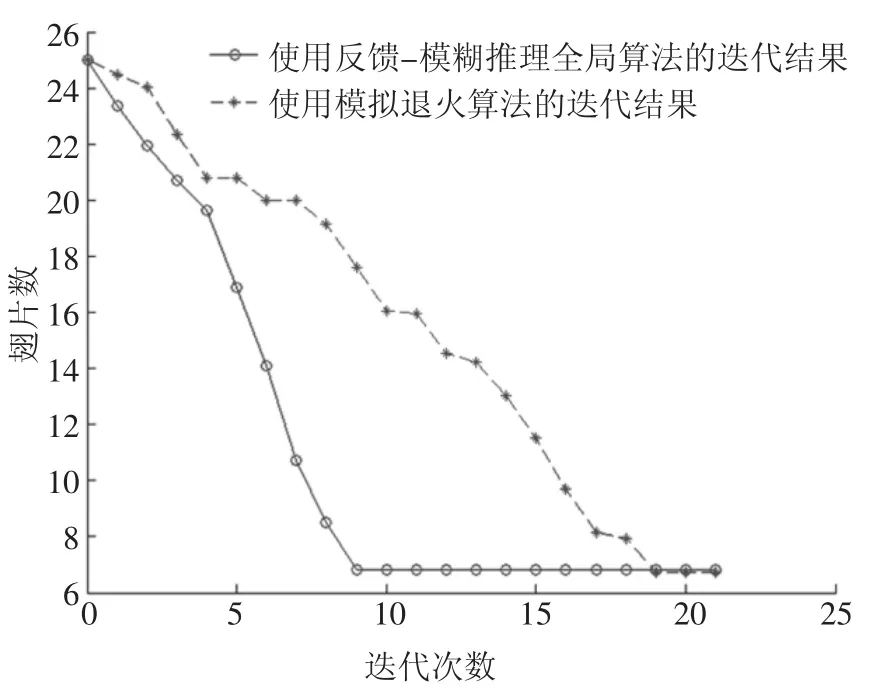
图7 反馈-模糊推理全局算法和模拟退火算法计算翅片数的迭代结果Fig.7 The iteration results of fin number computation by feedback-fuzzy inference global method and simulated annealing algorithm

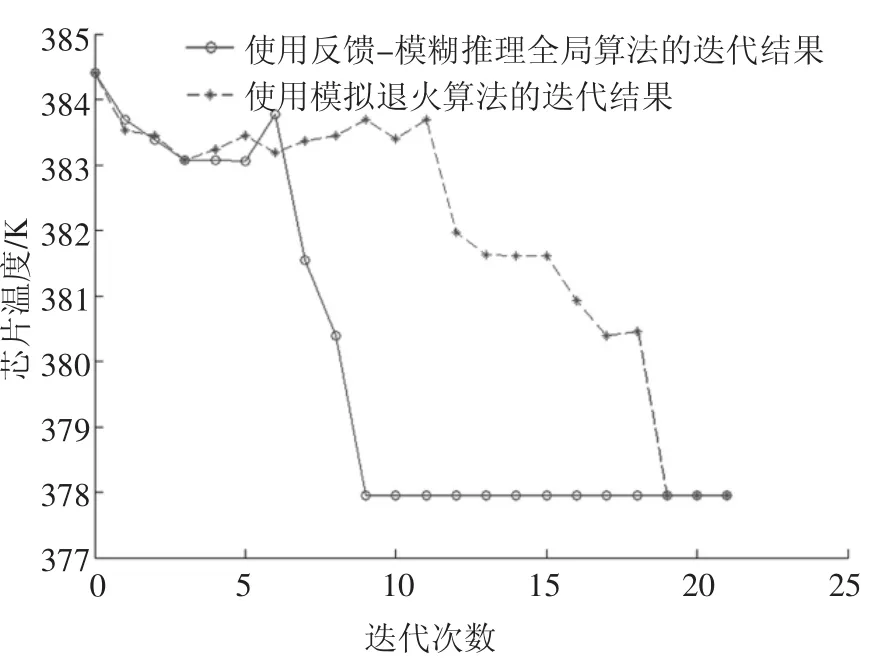
图8 反馈-模糊推理全局算法和模拟退火算法计算目标芯片温度的迭代结果Fig.8 The iteration results of temperature computation by feedback-fuzzy inference global method and simulated annealing algorithm

图9 常规模糊推理算法计算翅片数的迭代结果Fig.9 The iteration result of fin number computation by traditional fuzzy inference algorithm

图10 常规模糊推理算法计算目标芯片温度的迭代结果Fig.10 The iteration result of temperature computation by traditional fuzzy inference algorithm

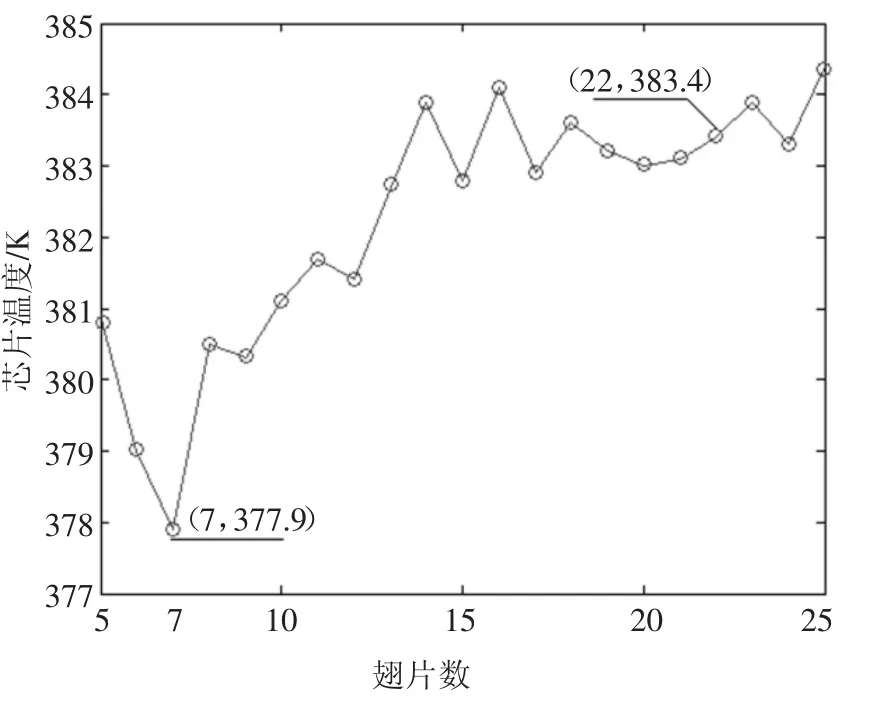
图11 采用不同翅片数量时仿真计算得到的芯片温度Fig.11 Chip temperature obtained by simulation with different fin numbers

由图7 和图8 可见，使用模拟退火算法得到翅片数量n=6.5，2 号芯片温度为378.6 K，取整数得n=7；使用反馈-模糊推理全局算法得到翅片数量n=6.9，2 号芯片温度为377.9 K，取整数得n=7.反馈-模糊推理全局算法在第9 次迭代时迭代终止，模拟退火算法在第19 次迭代时终止，故反馈-模糊推理全局算法的计算效率高于模拟退火算法.

由图9 和图10 可见，使用常规模糊推理算法得到翅片数量n=22.34，2 号芯片温度为383.57 K，取整数得n=22.由图11 可知n=22 时2 号芯片温度为383.4 K，n=7 时2 号芯片温度为377.9 K.常规模糊推理算法在相同条件下无法得到正确结果.

由图11 可知，反馈-模糊推理全局算法结果准确且有效避免了局部最优，反演精度略高于模拟退火算法.

综上所述，反馈-模糊推理全局算法可以有效求解传热学规律无法定量描述的传热学反问题，避免陷入局部最优，其计算精度和迭代效率均高于设置相同的模拟退火算法.利用反求结果得到的最佳翅片数量n=7 进行仿真，得到的芯片温度云图见图12，3 个芯片最高温度均低于393 K，结果符合要求.

图12 当翅片数为7 时的芯片温度云图Fig.12 The legend of chip temperature when 7 fins were used

4.2 初始值对结果的影响

使用反馈-模糊推理全局算法在初始翅片数n（0）分别为10 和5 时，计算翅片数的迭代结果和目标芯片温度的迭代结果分别如图13 和图14 所示.

图13 当初始翅片数分别为10 和5 时计算翅片数的迭代结果Fig.13 The iteration results of fin number computation with initial fin number of 10 and 5

图14 当初始翅片数分别为10 和5 时计算目标芯片温度的迭代结果Fig.14 The iteration results of temperature computation with initial fin number of 10 and 5

由图13 可知，初始翅片数n（0）分别为10 和5时的迭代结果均为n=7，可见对于相同的设计问题，初始值只影响迭代次数，不影响迭代结果.

4.3 温度测量误差对结果的影响

给2 号芯片的温度添加随机测量误差Tmea=Tmea+ξ×r，其中ξ 是测量误差的标准偏差，r 是一个取值范围在[-1，1]的随机数，当ξ 分别为1%、3%、5%时，迭代结果如图15 所示.由图15 可知，在计算过程中随迭代次数的增加，误差对迭代结果的影响逐渐增大.当ξ 分别为1%、3%、5%时的最终迭代结果分别为n=7.22、7.75、7.94，反演偏差在可接受范围之内，该算法可以有效对抗输入信息误差.

图15 不同标准偏差输入时的迭代结果Fig.15 The iteration results with different standard deviation

5 结论

本文针对常规模糊推理方法的局限性提出了一种结合模糊推理、反馈思想和模拟退火算法的反馈-模糊推理全局算法，并从传热学反问题的角度对电动汽车集成控制器中风冷散热器的几何结构设计问题进行了求解.

计算结果表明，相对常规模糊推理算法，反馈-模糊推理全局算法可以应用于非单调或无法定性描述传热学规律的热设计问题中，且具有迭代精度高、收敛速度快、计算结果受初始值影响小等特点.通过讨论输入误差对计算结果的影响验证了该算法具有良好的鲁棒性和抗不适定性.

该反馈-模糊推理全局算法拓展了模糊推理方法的应用范围，可以为反问题、结构设计和优化提供参考.