基于动态燃料成本双层优化的燃煤发电企业管控模型

廖志伟，张文锦，陈琳韬，黄杰栋，庄竞

（华南理工大学 电力学院，广东 广州 510641）

随着电煤价格双轨制取消以及供给侧结构性改革引起电煤市场波动性增强，电煤价格连年走高[1]，直接导致燃煤发电企业生产成本提高；与此同时，风电、光电等低边际成本可再生能源参与电力市场竞争，导致市场出清价格接近或低于燃煤机组发电成本，并使得燃煤电厂中标发电量进一步降低[2].以燃煤电厂为代表的传统火电企业陷入电力市场运营困境，甚至出现亏损情况[3].因此，火电企业亟须优化现行运营策略以降低发电成本从而增强电力市场竞争力.

燃煤电厂的燃料成本占据发电成本的70%～80%，分别受电煤采购入厂环节、电煤库存管理环节及电煤入炉掺烧环节影响[4]，国内外不少学者对燃煤电厂燃料管控策略展开研究.文献[5-7]将电厂电煤库存管理与电煤采购决策相联系，对电煤库存管理问题建立混合整数线性规划模型，在不同煤炭供应商中选择最优采购组合方案.文献[8-9]讨论不同风险类型电厂决策者考虑现货价格波动情况下的不同燃煤采购策略，在不同煤炭供应商中求解最优采购组合方案.文献[10]结合动力煤期货和现货市场，优化电厂库存策略，减少电煤库存对电厂流动资金的占用.文献[11]以电厂年度收益条件风险价值最小为目标，考虑煤价和上网电价不确定性，运用线性规划对电厂燃煤库存优化模型求解.然而，上述文献研究燃煤电厂库存管理策略和采购方案是基于电煤发电消耗固定的前提，根据电煤价格波动，尽可能选择购买低价煤，忽视电厂内锅炉混煤掺烧比例对发电燃料成本的影响.为此，也有不少学者研究锅炉最佳混煤掺烧方案.文献[12]通过调整混煤掺烧方案使其燃烧特性接近锅炉设计目标煤质，并优化煤场库存存放位置减少入炉混煤调运时间.文献[13-15]研究不同混煤掺烧方案下对锅炉气体排放和碳化合物排放的影响，优化锅炉燃烧对环境污染的排放.文献[16]建立入炉混煤标准煤单价价差模型计算燃煤电厂燃料成本，证明直接掺烧便宜劣煤不能有效降低燃煤成本.文献[17-18]兼顾燃煤电厂锅炉运行的安全性和经济性，通过掺烧试验得出保证锅炉安全运行下经济性较好的混煤掺烧方案.

综上可知，传统火力电厂由于信息系统孤岛及燃料部门和采购部门对发电可靠性和生产经济性的侧重点不同，混煤掺烧方案难以与电煤采购方案实现协同全局优化燃料管控.

随着计算机、数字化和大数据技术的发展，使燃料管控整体动态全局寻优成为可能，本文提出一种综合考虑发电可靠性和生产经济性的燃料成本双层优化模型，通过多个环节动态耦合，将部分环节局部静态优化转换成全局动态优化燃料管控方案.首先，梳理燃煤电厂传统燃料管控流程工作逻辑，分析燃料管控对发电成本的影响；其次，分别构建上层电煤采购库存混合整数规划模型和下层锅炉混煤掺烧非线性优化模型，其中，上层模型以采购成本和库存成本最低为目标函数，确定采购方案，向下层模型传递可用电煤；下层模型以锅炉燃烧混煤平均标准煤单价最低为优化目标，确定掺烧方案，并向上层模型传递电煤需求计划.然后，将上下层模型交替迭代协调优化，并使用混沌映射初始化和高斯变异结合的改进灰狼优化算法求解燃料成本双层优化模型；最后，以某燃煤电厂为算例验证双层优化模型的可行性.

1 燃煤电厂运营机制及双层优化模型

1.1 燃煤电厂运营机制成本模型

燃煤电厂的燃料成本与其燃料管控水平息息相关，电煤从采购到生产的全过程如图1 所示.

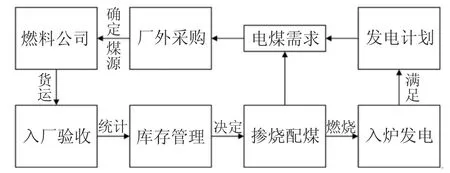
图1 燃料管控流程Fig.1 Fuel control process

影响燃料成本的过程主要为厂外采购环节、电煤库存管理环节和锅炉混煤掺烧环节.在不同的环节，发电燃料成本有不同的表现形式，为方便本文描述，做如下定义：

入厂原煤单价pi，m，反映电厂采购水平:

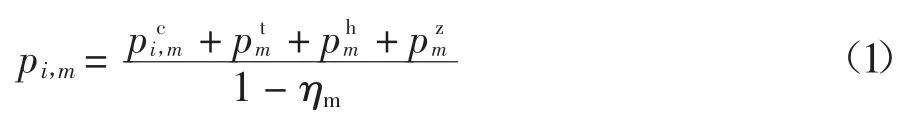
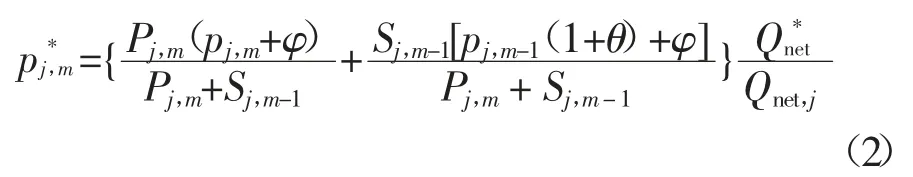
式中：pi，m为第m 周第i 种电煤入厂原煤单价为港口煤单价为入厂运费单价为入厂印花税；为入厂杂散费；ηm为运输损耗为第m 周第j类电煤的入炉标准煤单价；Pj，m为当周该类煤采购量；Sj，m-1为上周该类煤囤积量；φ 为电煤库存管理费用单价；θ 为电煤囤积导致的资金积压利息月利率；、Qnet，j分别代表标准煤和对应电煤低位发热量；Nj为燃煤电厂库存电煤分类种数为第m 周混煤入炉标准煤单价；εj，m为第j 类电煤在第m 周的掺烧比例.

1.2 燃料成本双层优化模型

由1.1 节可知，采购环节与库存管理直接相关，本文针对对应环节分别建立电煤采购库存模型和混煤掺烧优化模型.考虑到采购环节和配煤环节是相互影响、相互制约的关系，将二者构建为如图2 所示的燃料成本双层优化模型.

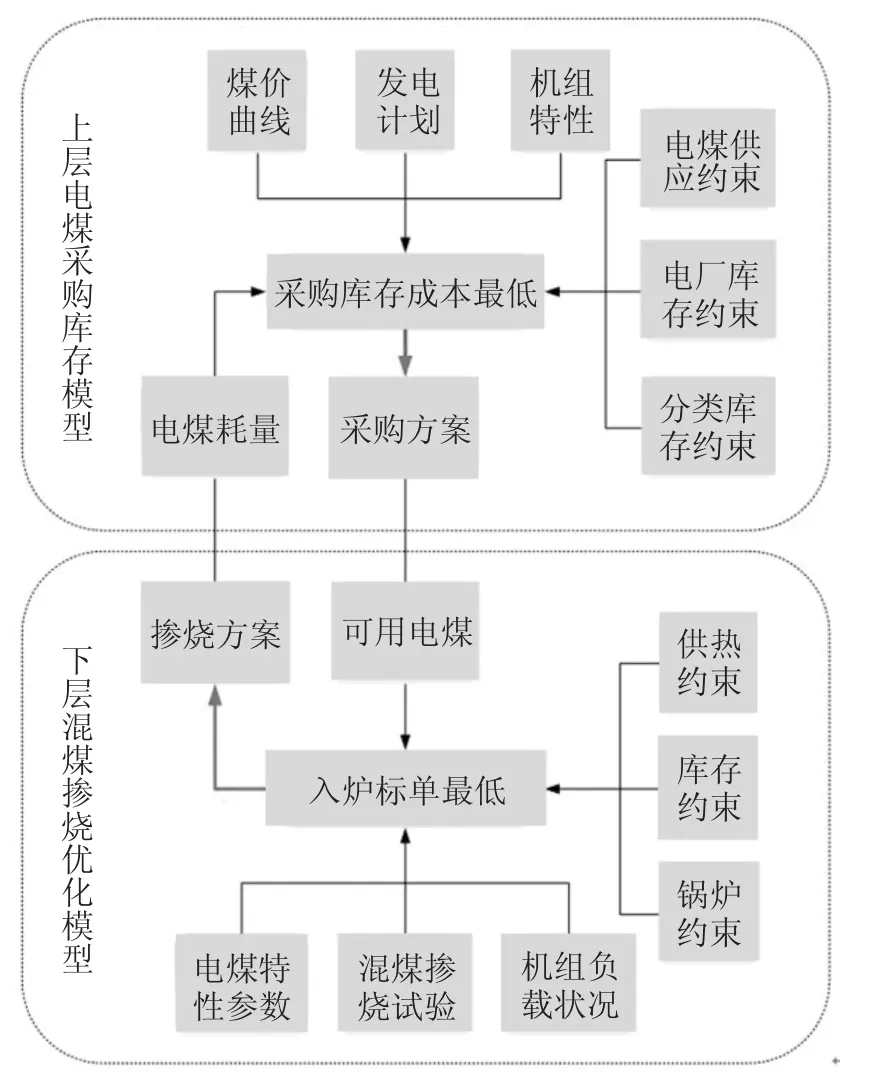
图2 燃料成本双层优化模型Fig.2 Bi-level optimization model of fuel cost

上层电煤采购库存模型中，以电煤采购总成本最低为目标函数，采购周期内各类电煤采购量作为决策变量，考虑电厂库存和煤炭供应满足最小发电计划需求从而保证发电可靠性，求解采购库存方案并向下层混煤掺烧优化模型传递电煤入厂标准煤单价和可用电煤.

下层混煤掺烧优化模型中，以入炉混煤平均标准煤单价最低为目标函数，决策变量为各类电煤掺烧比例，约束条件以供热约束、库存约束和锅炉约束的形式保证锅炉燃烧生产的可靠性，通过求解混煤掺烧方案向上层优化模型传递电煤消耗情况.

通过迭代上下层模型协同优化目标函数，避免单独求解模型时陷入燃料成本局部最优情况，探寻全局最优燃料管控方案.

1.2.1 电煤采购库存模型

1）目标函数.本文在文献[4]基础上将电煤采购总成本C 分为厂外购入成本C1和厂内仓储成本C2，厂外购入成本C1集中体现为入厂原煤单价和电煤采购量，厂内仓储成本C2包括电煤库存管理费用和采购资金积压利息：

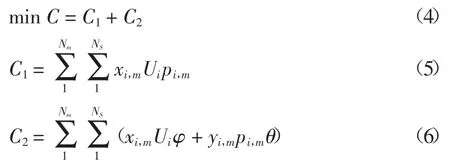
式中：Nm为采购周期内周数；Ns为可选电煤供应商数；整数型决策变量xi，m代表电厂第m 周向第i 个煤炭供应商的购买批次；Ui代表向第i 个煤炭供应商单一批次电煤购买量；yi，m为跨月提前采购电煤数量.

2）约束条件分为供货约束，电厂库存约束，分类库存约束.

①供货约束.根据有无月前预订合同，燃煤电厂向电煤供应商订购的动力煤可分为长协煤和现货煤.长协煤单月采购量应在合同的预定范围内，对应供货约束如下：

②电厂库存约束.由于电厂存放煤炭场地有限，同时要保证最小连续发电天数，电煤库存数量介于电厂库存上下限之间，即

式中：Pm为电厂第m 周的电煤采购总量为电厂第m 周的电煤消耗总量为电厂第m 周的电煤库存总量，由式（8）（9）计算得到和分别为电厂总库存下限和上限.

③分类库存约束.为保证电厂生产安全连续进行，各类电煤库存数量应保持在安全范围内，即

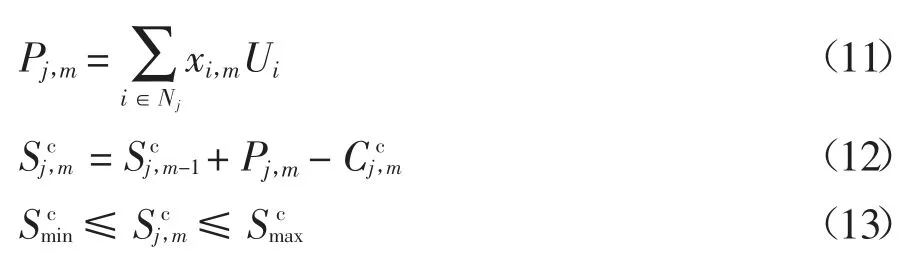
1.2.2 混煤掺烧优化模型

1）目标函数.当发电计划确定时，机组发电所需的标准煤耗量确定，发电成本取决于入炉混煤平均标准煤单价，因此混煤掺烧优化模型以最低入炉混煤平均标准煤单价为目标函数[16]：

2）约束条件分为供热约束，库存约束，锅炉约束.

①供热约束.锅炉燃烧提供的热量须满足根据反平衡法计算机组发电的热量需求，即

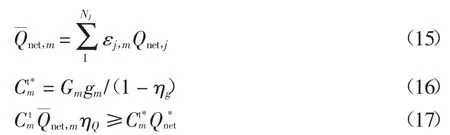
式中：Qnet，m为混煤平均低位发热量，满足混煤掺烧线性可加性为第m 周的发电标准煤耗量；Gm为第m 周的发电量；gm为第m 周的机组发电单位标准煤耗量；ηg为厂用电率；ηQ为锅炉热效率，受混煤低位发热量影响，由混煤试烧试验得出.

②库存约束.机组发电使用电煤耗量受电厂当周可用电煤限制，即

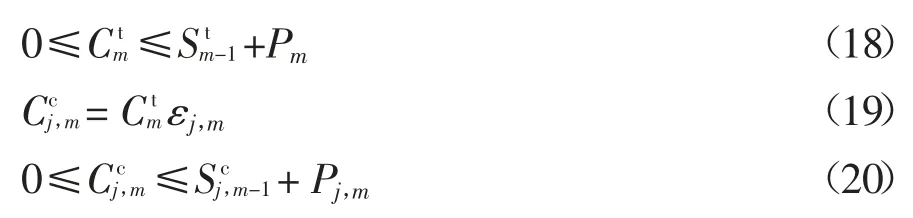
③锅炉约束.为保证锅炉安全生产，混煤煤质应在锅炉燃烧设计范围内，具体如下：

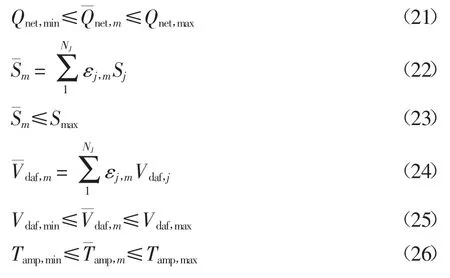
2 灰狼优化算法

灰狼优化算法（Grey Wolf Optimizer，GWO）是Mirjalili 等[19]在2014 年受野外狼群的等级机制和狩猎方式启迪而提出的群体智能优化算法，在低维寻优问题中表现出较好的搜索能力和收敛速度，对混煤掺烧非凸优化模型求解有不错的适应性和鲁棒性，但是面对电煤采购库存模型中高维的可行解空间和复杂时空连续性约束情况，GWO 算法出现种群个体质量低和早熟收敛问题.为此，本文从种群初始化和个体变异两方面出发，分别使用混沌映射种群初始化算子和高斯变异算子改进灰狼优化算法（Improved Grey Wolf Optimizer，IGWO）.

2.1 改进灰狼优化算法

2.1.1 混沌映射种群初始化算子

电煤采购库存模型的求解质量依赖于种群初始化的采购库存方案分布情况，优秀的初始化种群采购库存方案尽可能在可行解空间呈现多样化，对算法的全局搜索能力和收敛速度都有不错的提升.相较于计算机伪随机数生成，非线性的混沌映射具有初值敏感性和空间遍历性的特点，可以提高初始化方案的多样性.

本文采用Tent 映射产生[0，1]随机混沌序列，再通过等比放大映射为初始化电煤采购库存方案种群，Tent 映射的表达式如下：

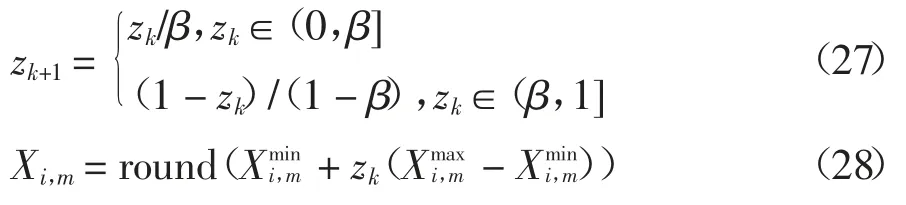
式中：zk为初始随机数；β 为混沌因子控制参数，取β=0.3分别为第i 种电煤第m 周可购订单最大和最小值，取整后为电煤采购模型初始整数决策变量Xi，m.

2.1.2 高斯变异算子

针对GWO 算法在电煤采购库存模型求解中早熟收敛的情况，本文受遗传算法的启发，在灰狼种群更新之后增加高斯变异算子以提高局部搜索能力.高斯变异算子计算公式如下：

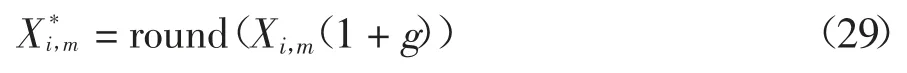
2.2 算法流程

IGWO 算法针对电煤采购库存模型的求解步骤为:

步骤1 设置狼群中采购库存方案总数，最大迭代次数，根据约束条件确定电煤采购库存模型可行域；

步骤2 根据式（27）（28）混沌映射初始化种群电煤采购方案；

步骤3 随机选择部分灰狼个体方案按式（29）进行高斯变异，检验种群内灰狼个体方案是否满足约束条件，对于越限采购库存方案映射到约束可行域内；

步骤4 计算各方案采购总成本并选择最优的3个采购库存方案作为灰狼领袖α、β 和δ 狼，其余灰狼ω 按领袖狼信息更新位置；

步骤5 重复步骤3、4，直至达到最大迭代次数；

步骤6 算法结束，输出α 狼对应的电煤采购库存方案的采购总成本并向混煤掺烧优化模型传递可用电煤.

求解燃料成本双层优化模型算法流程如图3 所示，其中取相邻迭代入炉平均标准煤单价最大差值为双层优化模型收敛判据：

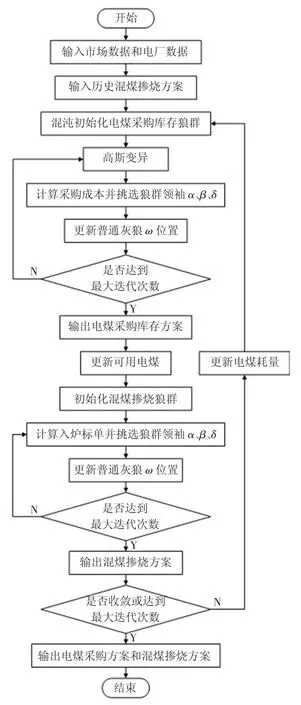
图3 燃料成本双层优化算法流程Fig.3 Bi-level optimization algorithm flow of fuel cost

3 算例分析

本文选择某2×600 MW 燃煤电厂某年6 月至7月期间连续8 周的燃煤管控决策算例分析.选取6月至7 月作为采购周期是因为7 月为迎夏用电高峰，全国发电量显著增加，动力煤价格同期上涨，是燃煤电厂重点关注的调整库存时段.该电厂库存信息、锅炉约束和发电计划分别如表1、表2 和表3 所示；以中国2.3×104kJ 煤炭指数（Chinese Coal Index 5500，CCI5500）作为动力煤价格参照，如图4 所示；具体的电煤价格和煤质信息见表4.

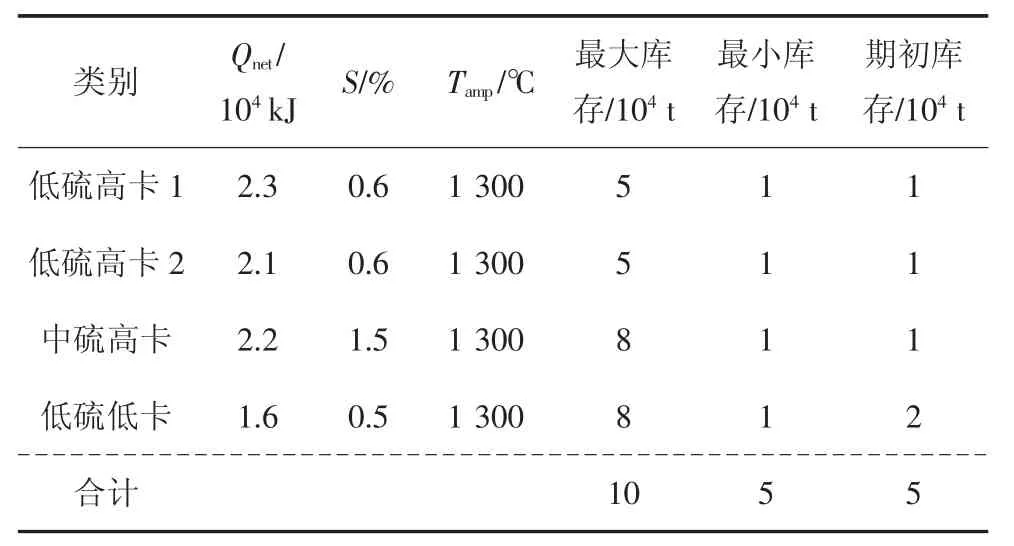
表1 电厂库存信息Tab.1 The power plant inventory information

表2 锅炉信息Tab.2 The boiler information

表3 发电计划Tab.3 The power generation plan

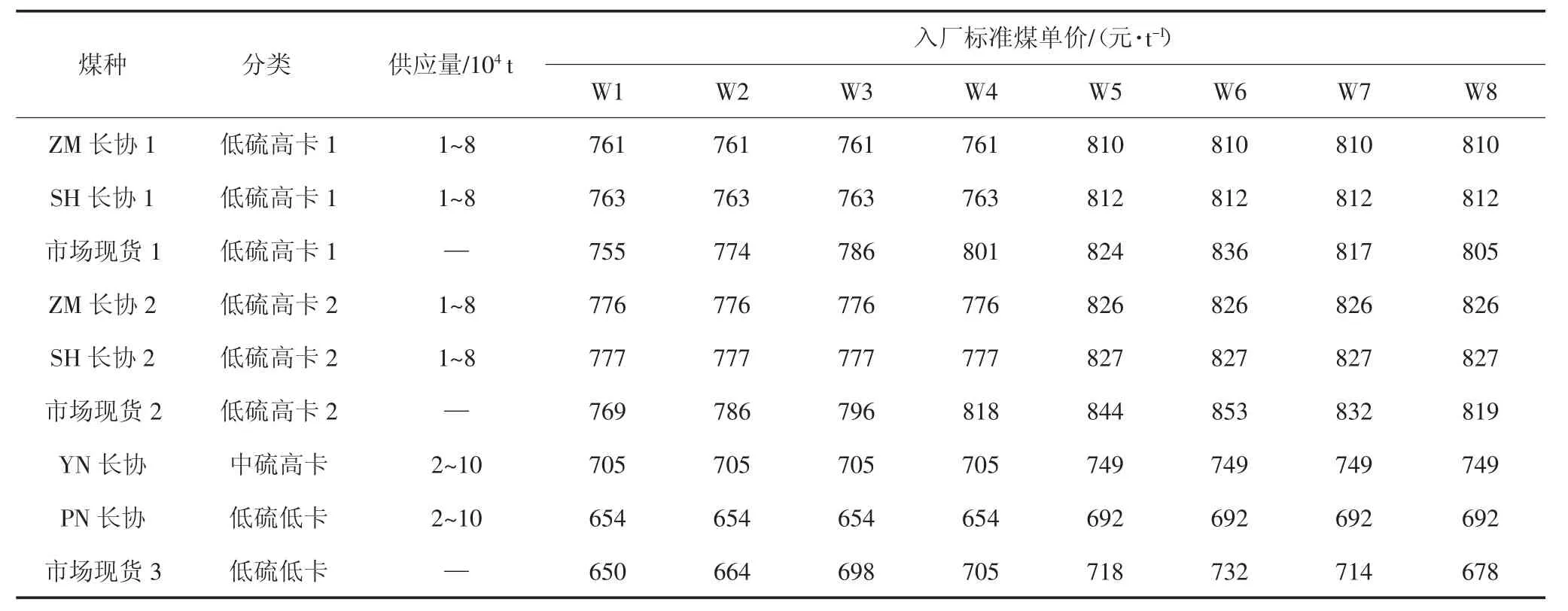
表4 可选动力煤信息Tab.4 The optional thermal coal information

图4 CCI5500 动力煤价格曲线Fig.4 The thermal coal price curve of CCI5500

输入电厂历史混煤掺烧方案，设定最大迭代次数为50，通过求解电煤采购库存模型获得如图5 所示的电厂库存曲线.在采购方案周期内，燃煤电厂在动力煤市场价格上涨时期以购买长协煤为主，稳定发电成本；在现货煤价格较低时，增加现货煤采购量以降低燃料成本.另外，燃煤电厂通过提前采购下周发电用煤，降低采购成本，实现“价低拉库存，价高保发电”的采购优化目标.

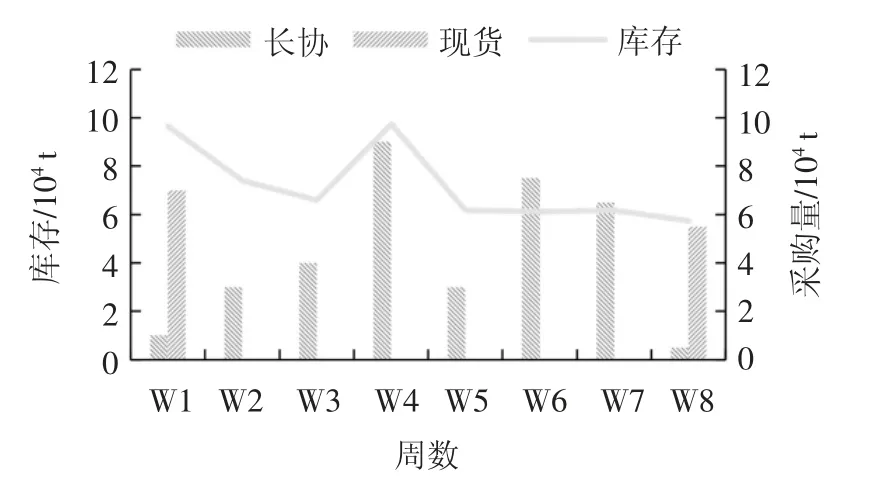
图5 燃煤电厂库存曲线Fig.5 Coal-fired power plant inventory curve

图6 为遗传算法（Genetic Algorithm，GA），粒子群优化算法（Particle Swarm Optimization，PSO）以及原始GWO 算法与IGWO 算法求解性能对比结果.由图6 可知，4 种求解算法均能在最大迭代次数内收敛，相较于GA 算法和PSO 算法，2 种GWO 算法的采购成本均能迅速下降到最优解附近，然而原始GWO 算法陷入局部最优，收敛的解质量最差.对比4种算法的收敛速度和解的质量，说明IGWO 算法在电煤采购库存模型求解拥有更优的全局搜索能力和求解精度.

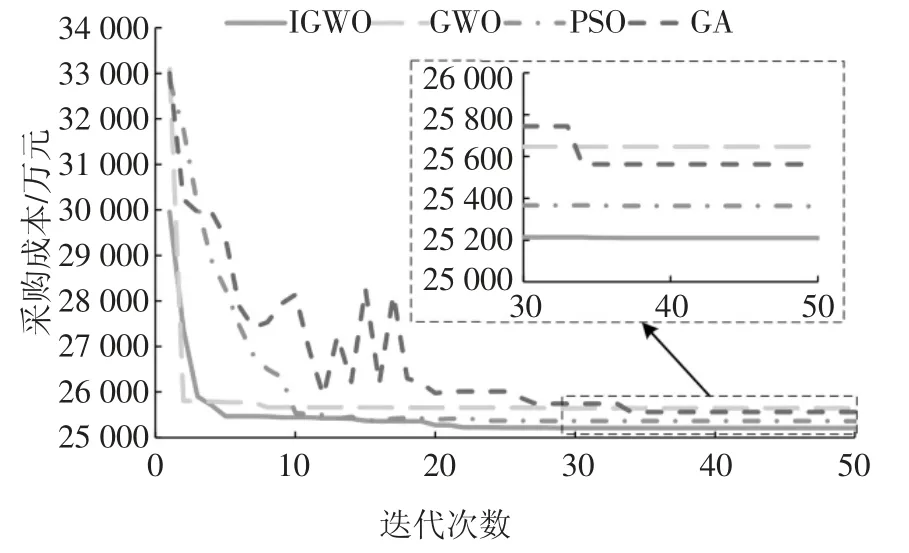
图6 优化算法求解对比结果Fig.6 The results of optimization algorithm were compared

将上述使用电厂历史混煤配比方案进行电煤采购库存模型求解设置为算例1；将经过一次混煤掺烧优化后再对电煤采购库存模型求解设置为算例2，模拟单独对电厂燃料管控环节优化的情形；使用本文提出的燃料成本双层优化模型模拟电厂整体优化燃料成本方案设置为算例3.

各算例各周入炉标准煤单价求解结果如表5 所示.算例2 平均单价较算例1 降低35.57 元/t，算例3较算例1 降低44.27 元/t，这是因为算例2 受限于电厂可用电煤的数量，混煤配比优化空间有限，而算例3 使用燃料成本双层优化模型，电煤采购方案与混煤配比方案协同优化，可以实现锅炉混煤配比方案主动优化效果.其次，得益于提前购入的低价长协煤，第5 周的平均入炉标准煤单价成为各算例中7 月单价最低周.另外，算例3 的第4 周和第7 周入炉标准煤单价在算例1 单价相同的情况下分别较第3 周和第6 周降低2.3 元/t、1.2 元/t，这是由于燃煤电厂事先签订的供应合同要求必须使用一定数量的高价电煤，当发电量升高时，耗煤量增高，燃煤电厂可以使用更多廉价动力煤，混煤平均入炉标准煤单价随之降低.

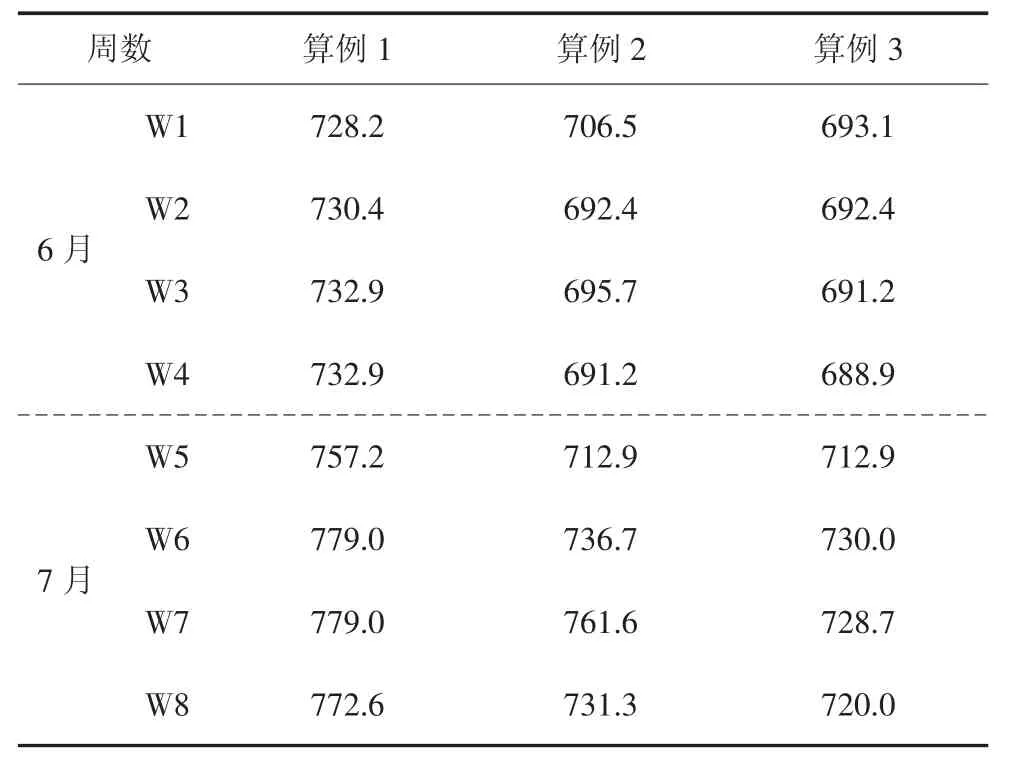
表5 入炉标准煤单价Tab.5 The unit price of standard coal in furnace 元·t-1

算例1、算例2 和算例3 电煤采购总成本分别为25 358.55 万元、23 611.74 万元和23 379.78 万元，算例2 和算例3 分别比算例1 降低1 746.81 万元、6.89%，1 978.77 万元、7.80%，说明对燃煤电厂燃料管控环节优化可以减少电煤采购成本.本文提出的燃料成本双层优化模型对电煤采购库存管理和混煤配比的协同优化处理可以更为明显地降低电煤采购成本，有效提高燃煤电厂的市场竞争力.

4 结论

本文构建一种燃煤电厂的燃料成本双层优化模型，并使用改进灰狼优化算法对其求解.算例结果分析表明：

1）对于电煤采购库存模型中可行解空间复杂且间断的情况，基于混沌初始化与高斯变异的IGWO算法的收敛速度和求解质量优于GA、PSO 与GWO，证明了IGWO 算法在该模型中具有良好的收敛性和精度.

2）对燃煤电厂燃料管控环节优化可以减少电煤采购成本，而燃料成本双层优化模型兼顾电煤采购方案和混煤配比方案的协同优化，对比传统燃料管控方案与单独管控环节优化方案，在降低采购成本和入炉标准煤单价方面更具优越性.