坐姿人体侧向振动试验、建模与参数识别
罗 霜,舒红宇
(1. 重庆交通大学 山区道路复杂环境“人-车-路”协同与安全重庆市重点试验室,重庆400074; 2. 重庆大学 机械传动国家重点实验室,重庆 400044)
0 引 言
汽车行驶过程中,由路面不平、加/减速、转向等引起的汽车振动,主要通过座椅传递到坐姿人体的脚、腿、臀和背部,引起人体全身振动[1]。侧向(左右方向)振动会大幅影响舒适性,长时间承受侧向振动,人的精神状态、工作效率与健康容易受到影响。研究坐姿人体侧向振动特性,有助于改善乘坐舒适性,也能够丰富人-椅动力学理论。
目前,国内外已有大量研究成果指向坐姿人体的垂向振动特性,但是仅有少数外国学者研究了坐姿人体侧向振动特性。G.F.BEARD[2]等在0.2~1.0 Hz间对侧向振动舒适性进行了较系统的研究,发现随着激振频率增加,受试者越发感到不舒服。与刚性座板相比,泡沫坐垫增大了座椅的传递率,意味着在低频侧向振动下,坐姿人体需要更大的肌肉张力以保持稳定坐姿,大腿和腰部会感到极其不舒服[3],但座椅靠背的支撑作用,会让不舒适感减轻[2,4]。侧向线振动和侧倾运动均会产生侧向加速度,并且两者对坐姿人体舒适性的作用频带不同,在分析靠背或者坐垫对舒适性影响时,需要考虑侧向加速度产生的形式[4]。虽然G.F.BEARD等深入研究了侧向加速度激振下的坐姿人体不舒适度与激励频率、座椅特征之间的关系,但是研究的频率较低,不能激发出坐姿人体的侧向主共振。人-椅系统存在显著非线性特性,其响应共振随测量方式、坐垫/靠背泡沫刚度[5]和厚度[6]、激励强度[7]等发生变化。S.MANDAPURAM等[8-9]在不同激振强度下进行了坐姿人体侧向振动试验,观测到受试者平均共振频率均在2 Hz左右,但试验中采用的座椅是刚性坐板加泡沫坐垫形式,与汽车座椅结构有明显差异,且并未观测到明显的二阶共振;G.J.STEIN[10]等在试验室环境下,利用汽车座椅在随机激励下对13名受试者进行了侧向振动试验并测量了志愿者视在质量,在0.30、0.98、1.92 m/s2的激振强度下,人体平均主共振频率分别为2.50、2.25、1.75 Hz。
目前,主要采用集中参数模型[11]、多体动力学模型[12]和有限元模型[13]来对坐姿人体振动进行描述。集中参数模型直观、易于理解,而被广泛使用,在集中参数模型中,大多数学者基于垂向激励建立坐姿人体垂向、垂向-纵向振动模型。对于侧向激振模型,文献[10]建立了4个三自由度模型来描述坐姿人体的侧向振动,但是缺乏对人体每个组成部分的具体描述。
为探究坐姿人体在低频大幅度激励下的侧向振动特性、辨识人-椅系统参数,笔者对10名21~28岁间的志愿者在0.5~8.0 Hz间进行侧向振动试验,以期得到了相应的传递特性数据,并建立相应的二自由度生物力学模型来描述坐姿人体侧向振动特性。
1 振动试验
1.1 试验对象
对10名青年志愿者进行侧向振动试验,年龄在21~28岁之间,平均身高170.3 cm,平均体重62.0 kg,体型特征如表1。
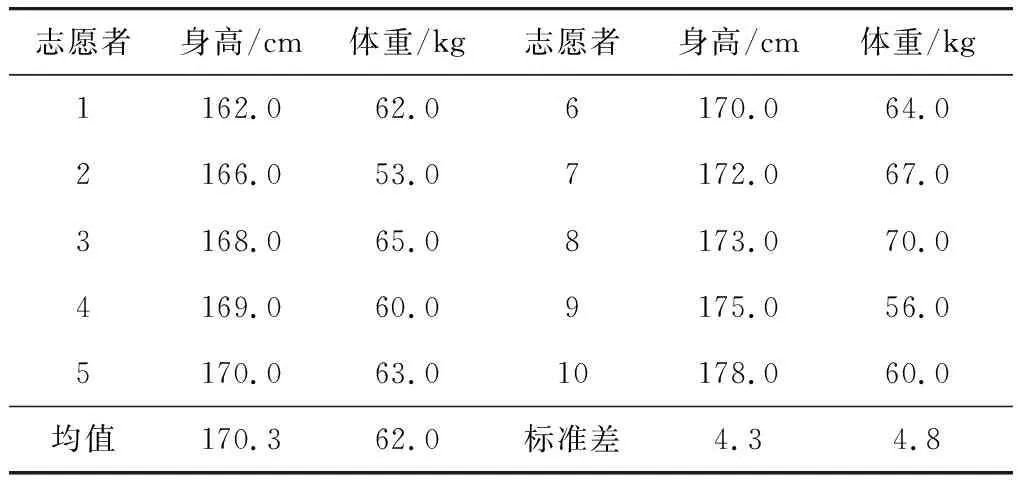
表1 志愿者体型特征Table 1 Body characteristics of volunteers
1.2 试验设备
振动试验台架由电机、座椅、传感器等组成,如图1。偏心轮、连杆和座椅底板组成基本的曲柄-连杆-滑块机构,将电机输出的旋转运动传递到座椅并转换成平移运动。


图1 振动试验设备Fig. 1 Vibration experiment apparatus
试验采用的惯性传感器由陀螺仪、加速度计和磁强计等组成,可测量人体运动的角速度(量程:-300~+300 °/s)和加速度(量程:-2~+2g),同时输出一个四元数q,且:
q=q4+q1i+q2j+q3k
(1)
式中:i,j,k为虚数单位并满足i2=j2=k2=-1;且q1,q2,q3和q4为实数。
四元数所对应的表征载体姿态变换的方向余弦矩阵可表示为[14]:
(2)
坐姿试验中人体振动剧烈,为避免传感器粘贴不牢靠引起较大测量误差,笔者设计加工了一种传感器固定装置。该装置分为上、下两个固定板,可通过弹性绳捆绑到人体躯干、四肢,能够较完美地与人体贴合,如图2。传感器MAHRS_0固定在底板的A点,测量底板即人-椅系统的输入信号;传感器MAHRS_1安装在下固定板的B点,测量下体(脚、腿、髋部和腹部)的响应信号;传感器MAHRS_2安装在上固定板的C点,测量上体(头、躯干、手和手臂)的响应信号。

图2 传感器安装位置及坐标系统Fig. 2 Sensor installation position and coordinate system
1.3 试验方案
试验中要求受试人员保持正常放松坐姿,双手自然放在大腿上,身体舒服地靠在座椅靠背上,眼睛平视前方。
电机旋转运动经过偏心轮、连杆传递到座椅底板,以对人-椅系统施加侧向振动激励。对志愿者施加单个频率点的振动激励,通过改变电机输出转速,进而对激励频率进行调节,以实现0.5~8.0 Hz范围内的加振,试验频率间隔0.1 Hz,每个频率点的振动维持时间约为30 s。这种单频激振方法振动时间长,振动能量集中,能够激发出试验频率范围内每个频率点的坐姿人体侧向振动特性,避免了随机带宽信号由于振动时间短(整个带宽内的暴振时间不超过120 s[15])、能量分散而无法完全激振出某些频率点的振动特性的缺点。对76个单频激励下MAHRS_0测量到的加速度时间历程进行自相关等变换,可得到激励幅值谱,如图3。
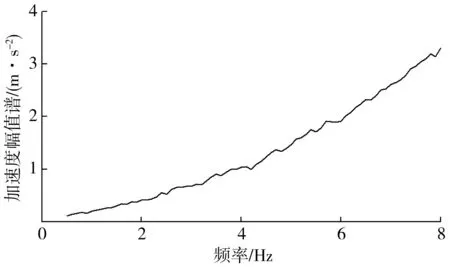
图3 激励频谱Fig. 3 Frequency spectrum of stimulus
试验数据采集处理过程中涉及到一个全局坐标系和三个局部坐标系:全局坐标系的x轴指向人-椅系统前后方向(纵向),y轴指向左右方向(侧向),z轴指向竖直方向;传感器的局部坐标系指向如图2,满足右手定则。
试验以坐姿人体上、下体质心处的传递率作为系统输出,而计算传递率时需要保证输入、输出信号在同一坐标系下,但在安装传感器时并不能保证各局部坐标系的y轴严格指向一致,需要对原始结果进行坐标变换。
首先,计算下、上体质心的空间位置,分别测量MAHRS_1的安装点到下体质心的初始位移矢量L1,及MAHRS_2到上体质心的初始位移矢量L2。再将测量的初始位移矢量和采集的响应加速度矢量通过坐标变换,转换到惯性坐标系下。然后,通过矢量平移变换,得到在此坐标系中的下、上体质心所在位置侧向加速度时域信号。最后,再做一次坐标变换,将经上述处理得到的时域响应变换到传感器MAHRS_0的局部坐标系中,以进行传递率计算。坐标变换过程如式(3):
(3)
式中:Q0,Q1,Q2分别为座椅、下体和上体对应的方向余弦矩阵;a1,a2分别为下、上体加速度响应的原始测量数据;a′1,a′2分别为加速度信号在传感器MAHRS_0局部坐标系下的表达。
1.4 试验结果
与激励幅值谱的计算类似,对MAHRS_1和MAHRS_2测量的加速度时间历程做相应变换即可得到输出信号的幅频响应。最后,根据式(4)计算得到坐姿人体侧向振动的传递率,如图4。
(4)
式中:f表示试验频率;H1e(f)和H2e(f)分别为根据试验数据所计算得到的下体和上体响应的传递率;A0(f)、A1(f)、A2(f)分别为座椅、下体和上体的频域幅值。

图4 下、上体传递率Fig. 4 Transmissibilities of lower and upper bodies
由4图可知:坐姿人体上体侧向振动共振频率在2.4~3.1 Hz之间,平均共振频率为2.8 Hz,峰值传递率在1.45~1.89之间;下体共振频率在2.4~3.2 Hz,平均共振频率为2.9 Hz,共振处(下体峰值)的传递率在1.53~2.38之间。下体共振频率比上体略高(p<0.05,符号检验),振动更剧烈(p<0.01);部分受试者上体激振频率在5.0 Hz以后存在比较明显的二阶共振。
笔者试验结果与先前的研究结果具有一定相似性。文献[10]观测到侧向主共振峰值出现的平均频率在2.5 Hz附近,座椅到人体的传递率幅值普遍分布在1.5~2.5之间。但笔者未观测到文献[10]提及的在0.75 Hz左右的共振,而是在5.0 Hz后发现一个二阶共振模态,这与文献[9]研究类似。
2 侧向振动模型
座椅对振动的传递取决于人椅界面的生物力学特性和座椅本身,在描述坐姿人体侧向振动模型中,需要考虑人体与座椅之间的相互作用[7]。研究显示,采用二自由度模型来描述坐姿人体的振动特性已有足够的精度[15]。因此,视人体为两个集中质量块,并考虑座椅与人体之间、质量块之间的连接,建立了侧向振动模型如图5。

图5 侧向振动二自由度模型Fig. 5 Two-DOF model exposed to lateral vibration
根据牛顿第二运动定律,可得坐姿人体的侧向振动运动微分方程:
kp(y2-y1)
(5)
kp(y1-y2)
(6)
式中:m1,m2分别代表下、上体质量;y0、y1、y2分别为座椅、下体和上体的侧向位移;kq1、kq2、kp和cq1、cq2、cp分别为连接点的刚度和阻尼系数。
对式(5)、式(6)两端同时进行傅里叶变换,可得到频域内的二自由度动力学模型:
(-ω2m1+jωcq1+kq1+jωcp+kp)Y1(ω)-(jωcp+
kp)Y2(ω)-(jωcq1+kq1)Y0(ω)=0
(7)
(-ω2m2+jωcq2+kq2+jωcp+kp)Y2(ω)-(jωcp+
kp)Y1(ω)-(jωcq2+kq2)Y0(ω)=0
(8)
因此,下体、上体的加速度传递率分别为:
(9)
(10)
式中:ω为圆频率,且ω=2πf;H1m(f)和H2m(f)分别为下体和上体的模型传递率。
模型中,下体和上体的惯性参数m1和m2可以用人体三维CAD模型来估算,而其它模型参数(刚度、阻尼)则需要通过参数识别进行估计。
3 参数识别
笔者采用求解速度快、抗干扰能力强并且不易陷入局部最优的遗传算法[16]进行参数识别,基于MATLAB遗传算法优化工具箱,采用式(9)、式(10)去拟合试验得到的下体和上体传递率幅值,即可辨识出坐姿人体侧向振动模型中的刚度阻尼参数。目标函数如式(11):
(11)
设置迭代次数100次或者函数误差小于1e-6为优化终止条件,以其中1名志愿者为例,优化过程如图6。进化过程中,在第23代和37代均出现了收敛的情况,但是紧接着又都发散了,这说明此时为局部最优解。在进化到第52代时优化收敛并未发散,说明第52代对应的解为全局最优。

图6 参数识别优化过程Fig. 6 Optimization process of parameter identification
为了定量评价模型对实测传递率的拟合效果,引入拟合度评价公式[17]:
(12)
式中:ε为拟合度;τe和τm分别为实测传递率与模型计算值;n为数据个数,取n=76。拟合度位于0~1之间,越大拟合效果越好。
对各个志愿者试验数据的拟合结果如图7,模型数据与试验结果匹配良好。在整个频段内,模型对实测上体传递率的拟合效果都比较好,只是在2名受试者的明显二阶共振附近,存在一定失配现象。除个别受试者外,模型能够良好地拟合6.5 Hz以下的下体试验数据,特别是主共振频率附近吻合良好。根据式(12)计算的拟合度如表2,上、下体拟合度的平均值分别为0.851和0.832,总体上讲,上体的拟合效果更佳。
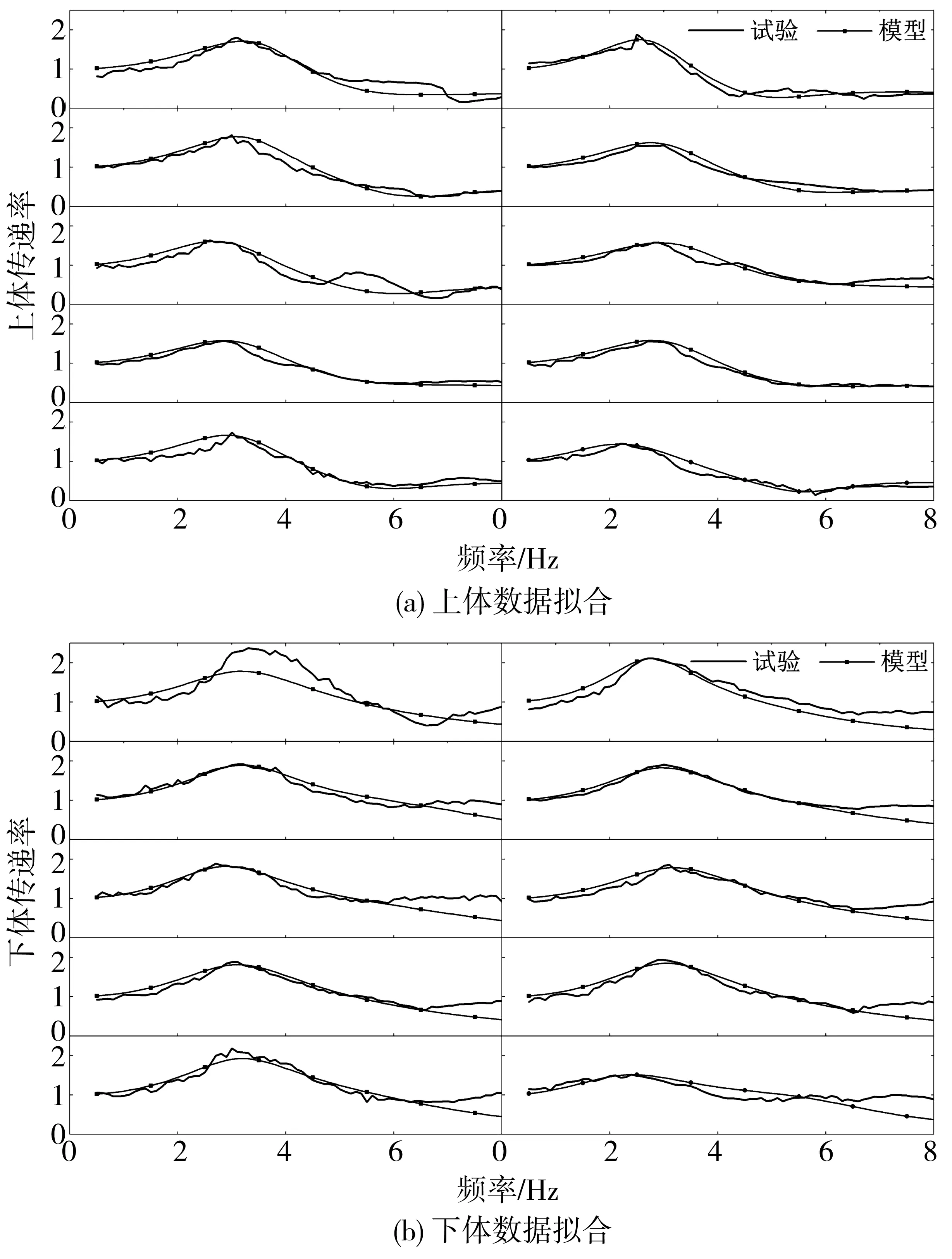
图7 传递率数据拟合Fig. 7 Data fitting of transmissibilities
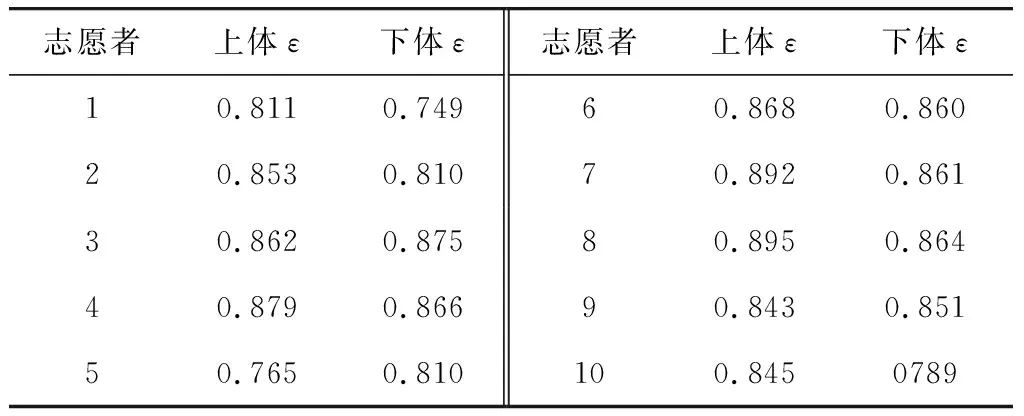
表2 志愿者拟合度Table 2 Goodness of fit for each volunteer
人-椅系统侧向振动的参数辨识结果如表3。从表3可以看出:由于志愿者个体差异,识别出的参数在一定范围内变动,且这些参数与志愿者身高、体重之间未见明显的相关性。
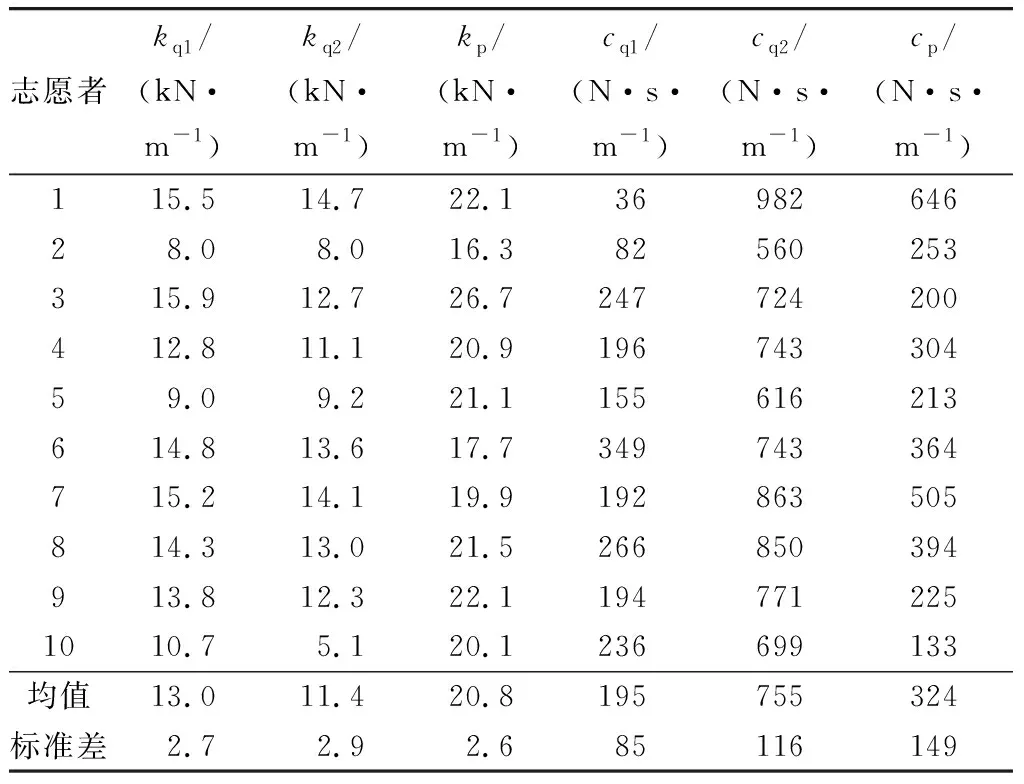
表3 识别的参数Table 3 Identified parameters
4 结 论
笔者对10名21~28岁之间的青年志愿者在0.5~8.0 Hz之间进行了侧向振动试验,发现下体侧向主共振峰出现在2.4~3.2 Hz,上体在2.4~3.1 Hz,并且上体在5.0 Hz以后存在比较明显的二阶共振;上体峰值传递率在1.45~1.89之间,而下体峰值传递率介于1.53~2.38之间;下体共振频率比上体略高,振动更剧烈。建立了二自由度生物力学模型对坐姿人体侧向振动特性进行描述,辨识了人-椅系统的侧向刚度阻尼系数,计算了模型对各个志愿者试验数据的拟合效果,上、下体拟合度的平均值分别为0.851和0.832。总体上讲,上体的拟合效果更佳。笔者研究成果不仅有助于改善乘坐舒适性,还丰富了人-椅动力学理论,可为座椅设计提供参考。

