特殊工况下擦窗机伸缩臂瞬态动力学研究
郑夕健,李清磊
(沈阳建筑大学机械工程学院,辽宁 沈阳 110168)
随着社会的进步,经济的大力发展,建筑物外墙和窗户的清洗、维修等作业需要通过设备完成任务,此时的擦窗机设备[1-2]的需求量逐渐增加。安装在高层建筑物屋顶上的轨道伸缩式的大型擦窗机应用的比较广泛[3]。伸缩臂是屋面轨道伸缩臂式擦窗机的主要承载和工作部件,擦窗机经常带着载荷做各种重复性动作[4-5]。在此过程中,擦窗机的各结构需要承受较大的动载荷,为了提高其工作的可靠性[6-8],需要对擦窗机突然提升、制动等方式以及其产生的冲击载荷作进一步研究。
目前国内对擦窗机伸缩臂的研究主要集中在典型工况下对其静力学分析,动力学分析,将整体结构进行优化设计[9-11]。在擦窗机制动、提升等特殊工况下研究瞬态分析的相关文献不是很多,数据分析的数量也很少,这样对擦窗机的机构优化缺少一些实际的建议[12-14]。
基于此,笔者主要研究伸缩横臂负载吊篮瞬间起升离地时和匀速下降制动时擦窗机伸缩臂结构的时间-载荷动态响应特性,并在瞬态动力学分析的基础上,提取动载荷、时间载荷步,对擦窗机伸缩臂分析;并用ANSYS仿真软件得到了两种工况下的位移变化规律与以时间步作为横坐标,结构位移变化和最大应力作为纵坐标的两组曲线,通过对比分析得出响应应力的最大值与加速度有关,并最后趋于稳定。
1 伸缩臂主要参数及特殊工况
1.1 擦窗机伸缩臂的主要性能参数
此次运用的机器型号为CWGS250型屋面轨道式擦窗机[15]。由基本臂、一节臂和二节臂组成[16]。主要技术参数:擦窗机伸缩臂完全伸出长度为15.2 m;完全缩回长度为4.6 m;擦窗机起升高度为173 m;配重臂的长度为4 m;羊角臂头质量为282 kg;起吊装置质量为135 kg;起吊装置额定载荷为282 kg;平台额定载荷为250 kg。
1.2 特殊工况简介
根据《擦窗机》(GB 19154—2017)规定,在正常工作或紧急情况下,擦窗机可以采取紧急制动措施。因此选择伸缩臂在负载时突然提升离地和伸缩臂吊重匀速下降时突然制动两种工况进行系统研究。在突然起升离地工况下,擦擦窗机臂头载荷从0开始加载,而在匀速下降制动时臂端应力最终会恢复到原有应力状态,最大应力值与负载速度变化率有关。
2 伸缩臂结构的瞬态动力学分析
2.1 伸缩臂端部动载荷计算
(1)工况一:吊重突然起升离地
在承载擦窗机人员的平台上放到起点时,起升的机构上钢丝绳是松弛的,提升装置在不承重时会产生一定加速度,当钢丝绳从松弛到拉紧的过程中,吊篮不受任何载荷,当钢丝绳绷紧状态后会受到载荷冲击,载荷的能量传送至整个擦窗机会到擦窗机产生一定的影响。起动阶段的三个过程如图1所示。
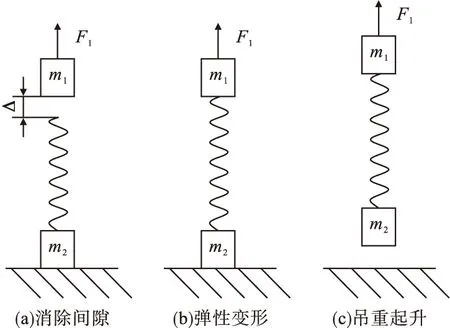
图1 起动过程三个阶段Fig.1 Three stages of the starting process
图1中,m1为电动机与传动装置的转动惯量等效到提升机卷筒边上的等效质量;m2为起吊重物质量;F1为启动圆周力。
t1为吊篮钢丝绳从松弛状态到将要受到拉力过程的时间,第一阶段时,0~t1内钢丝绳处于松弛状态;第二阶段时,t1~t2内,吊篮钢丝绳中的拉力逐渐增大,直到吊篮将要离地起升;第三阶段时,t2时间末吊篮突然起升离地,t3时刻吊船到达起升速度2 m/min。在力学分析中,第二阶段的传动系统与钢丝绳所承受力为
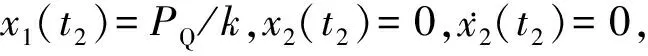
则吊篮钢丝绳受力为
F(t)=ke-ξωn(t-t2)[Asinωd(t-t2)+
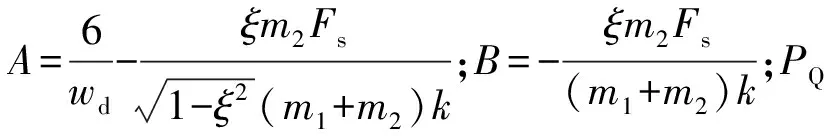
吊重突然起升离地时钢丝绳拉力随时间变化曲线如图2所示。使用MATLAB分析工作条件和中间时间曲线,缆车的钢丝绳在第一阶段受力为0,2 s后逐渐增加至7 832 N。大约8 s后,吊船钢丝绳趋于稳定。将方法运用在辅助吊钩上,钢丝绳承受的最大拉力为18 797 N,再次约为2 s后达到了稳定状态。根据工况一,其擦窗机的伸缩横臂端部承受的最大动载荷为26 629 N,同样在2 s后,载荷最终稳定在18 630 N。
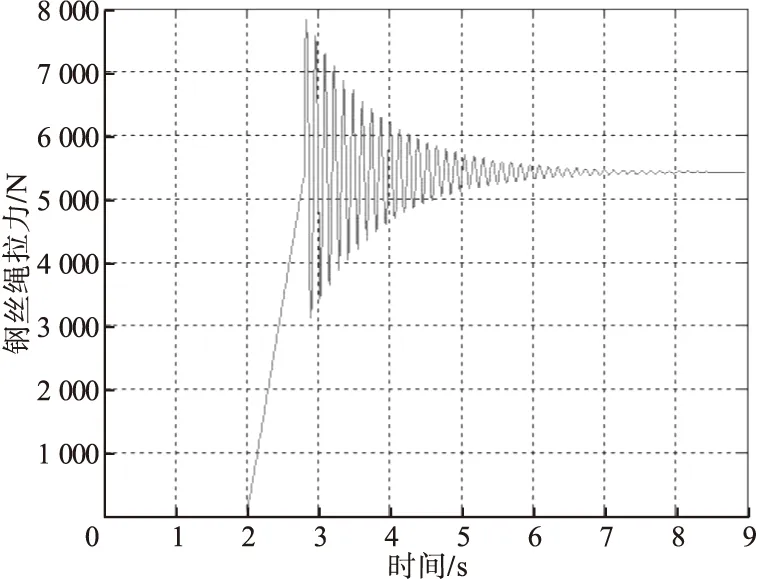
图2 钢丝绳拉力随时间变化曲线Fig.2 Curve of wire rope tension varying with time
(2)工况二:吊重匀速下降时制动
擦窗机的伸缩臂质量包括负载吊篮和操作人员的质量。吊篮的下降速度恒定时,卷扬机构突然制动。
吊篮以恒定速度下降时,钢丝绳处于张紧状态并受到伸缩臂的提升静载荷PQ的作用。当提升机突然停止时,吊篮受到惯性力的作用继续下降。此时,伸缩臂头因重物产生的载荷将在伸缩臂上产生冲击载荷,并产生振动。受力简图如图3所示。

图3 工况二动力学模型Fig.3 Dynamic model of the second working conditions
图中,F1为启动圆周力;x1为m1的位移;x2为m2的位移;k为钢丝绳的刚度;c为钢丝绳的阻尼。
系统的运动微分方程为
假设Fq恒定,令x=x2-x1,可得:

解得:
所以伸缩横臂的吊篮负载下降时突然制动,在这种工况下,钢丝绳上的力与三角函数关系式结合得:
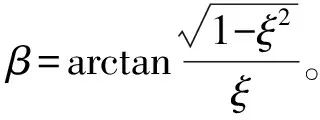
根据以上公式,吊篮和安全绳受与相位角有关。吊重匀速下降时钢丝绳拉力随时间变化曲线如图4所示。运用MATLAB软件分析了工况下钢丝绳中受力与时间的曲线图,其中钢丝绳所受到最大力为5 825 N,在持续2.5 s后,钢丝绳受的拉力不断减小,并呈波动状态逐渐趋于稳定。运用相同的方法获得,在辅助吊钩钢丝绳的最大拉力为13 975 N,在2.5 s后,辅助吊钩的钢丝绳逐渐趋于稳定,所以在工况二情况时的擦窗机的伸缩臂端部所承受的动载荷是19 790 N,在经过2.5 s后逐渐达到稳定值18 360 N。
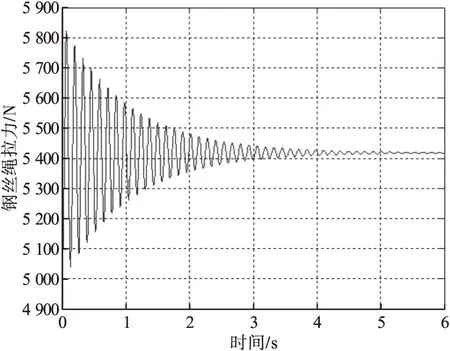
图4 钢丝绳拉力随时间变化曲线Fig.4 Curve of wire rope tension varying with time
2.2 伸缩臂有限元模型的建立
通过擦窗机伸缩臂的构型和运作特点,利用ANSYS软件将二节伸缩横臂的端部截面建立有限元模型。把伸缩横臂在建模之前进行一些简单的结构处理。忽略小零件和非承载构件;忽略焊缝的影响;简化结构直径尺寸小于10 mm的圆角和倒角。
笔者选用由Q345低碳合金钢经过冷变焊接过程的伸缩臂,因臂厚远小于其截面尺寸,故选择Shell81单元来进行模拟。根据采用Shell81单元进行网格划分的有限元模型如图5所示。

图5 伸缩臂有限元模型Fig.5 The finite element model of telescopic arm
2.3 伸缩臂瞬态动力学求解原理
笔者选用计算动力学对擦窗机伸缩臂进行瞬态动力学分析,根据模型的建立,将模型导入至瞬态动力仿真中,获得瞬间动态平衡方程:

式中:M为质量矩阵;C为结构阻尼矩阵;K为结构刚度矩阵;x为位移矩阵;F(t)为作用力向量[7]。
工况一:吊重突然起升离地
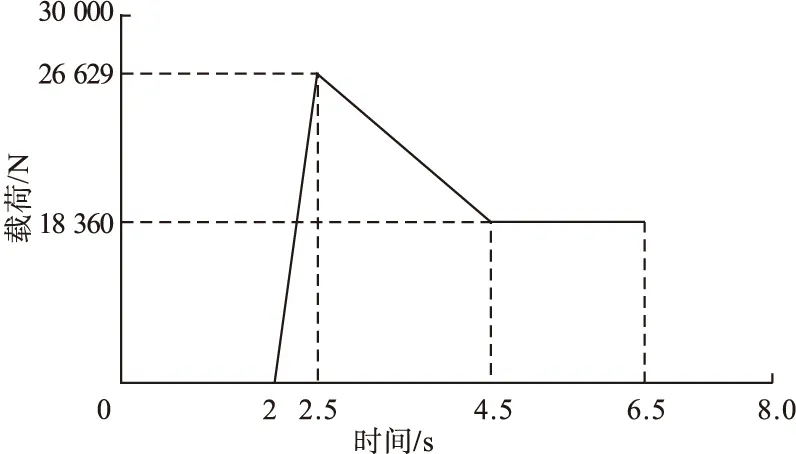
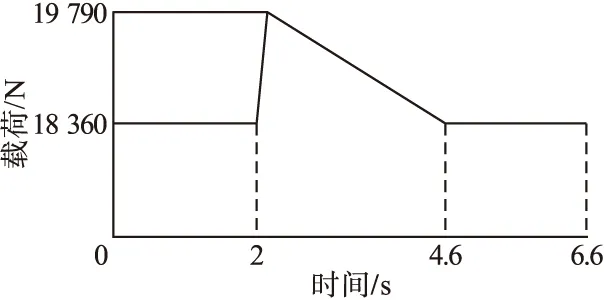
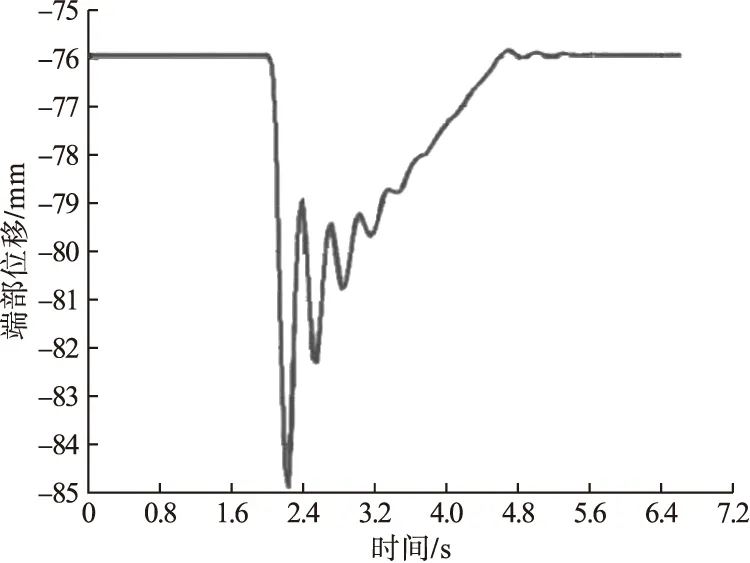
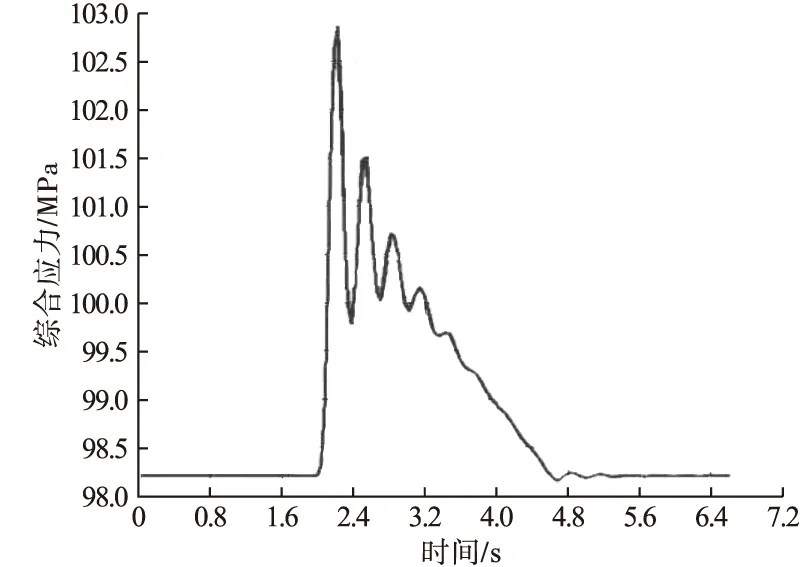
当t1 由动力学知识可知,伸缩臂的稳态响应为该振动方程的特解: 伸缩臂在瞬态响应时的预期对应的线性齐次微分方程的解: y=Ye-ζωncos(ωdt-φ). (11) 根据以上可以得出伸缩横臂的总位移的相应关系为 y(t)=y+y*=Ye-ζωncos(ωdt-φ)+ 式中:ωd为阻尼自然频率;且有ωd=ωn(1-ζ2);Y为位移矩阵;ζ为阻尼比;ωn为固有频率;k为等效刚度系数;ω为主要响应频率;φ为相位。 其中,K为伸缩臂等效刚度。 当t>t2时,既重物刚刚离开地面,这时重物将随着伸缩臂一起做自由振动,即kt=0,微分振动方程可以变换为 此时,对应的位移响应为 y(t)=ye-ζωncos(ωdt-φ). (16) 则此阶段对应的振幅和相位为 工况二下擦窗机伸缩臂瞬态动力学分析与工况一的过程时相似的,因此不再重复叙述。 综上分析可得在整个过程中伸缩臂的位移响应表达式为 y(t)= (19) 在模态坐标变换后再利用ANSYS中的模态叠加法再求解,其目的是将原有空间结构通过瑞利利兹变换和动力学方程移交到模态空间去求解。 ANSYS软件的瞬态动力,初始条件一般设定在0位移和0加速度的状态。若在初始非零状态时,可以将位移和加速度增加小量的步长。在每一时间对应的步长都要小于周期的1/20,这样才能保证计算结果的收敛性和准确性[8]。笔者选用的步长时间是0.01 s。根据《起重机设计手册》,起重机金属结构的阻尼比为ζ=0.008~0.05,取阻尼比为ζ=0.05。 在仿真的有限元模型中,所有螺栓连接的结构都采取了节点耦合的方法。在擦窗机固定横臂尾端以及二节臂前端进行刚化处理,在处理到一个节点后再添加MASS21的质量单元。笔者应用ANSYS瞬态动力学分析中的缩减法进行分析。 将参数输入ANSYS的瞬态动力学分析模块中,同时进行动分析求解,可以得到伸缩臂结构的最大应力和位移随时间-冲击载荷的瞬态响应特性曲线,分析两种特殊工况时伸缩臂的最大位移及最大应力随时间-冲击载荷的动态响应特性及变化规律。 伸缩横臂的负载吊篮从地上拉起,对此状态进行瞬态动力学分析。首先利用缩减法,定义主自由度的方向为伸缩臂端部受力的方向。具体运行状况曲线如图6所示。在不同的时间节点上,发生的载荷量随着时间变化而变化。0~2 s的过程属于空载过程,绳子受力的作用向上拉,当拉动吊篮时候伸缩横臂的端面产生了大量的载荷,吊篮被抬起时的载荷达到最大。2.5~4.5 s时,吊篮处于加速度逐渐减小,速度趋于稳定。4.5~6.5 s时,加速度为零速度变为匀速运动,其载荷也慢慢稳定到18 360 N。 图6 吊重突然起升离地时载荷-时间关系曲线Fig.6 Load-time curve when hoisting suddenly rises off the ground 伸缩臂的端部是发生最大位移的地方,方向为竖直向下,伸缩臂端部时程曲线如图7所示。 图7 伸缩臂端部时程曲线Fig.7 The time-history curve at the end of telescopic arm 通过图7可以了解到伸缩横臂钢丝绳处于松弛状态,当吊篮受到冲击力时,钢丝绳从松弛到紧绷的状态其前端位移为32.016 mm。在整个吊篮离地的过程中伸缩横臂受到了极大的冲击力。伸缩横臂的端部最大位移102.71 mm,最终稳定在76.972 mm。在整体过程中,受到载荷后伸缩横臂的最大位移比稳定状态时增加了33.4%。在不考虑应力集中的情况下,图7中最低点2.5 s时的应力最大达到了117.859 MPa。 伸缩臂的二节臂上翼缘应力云图如图8所示。应力-时间曲线如图9所示。吊重突然起升离地时各时间参数如表1所示。 图8 二节臂上翼缘应力云图Fig.8 The stress cloud at the upper flange of the second arm 图9 应力-时间曲线Fig.9 Stress time curve 根据图9与表1可以得出,在提升机卷筒转动时,伸缩臂的基臂前端下翼存在综合应力。钢丝绳在受到拉力时从松弛到拉紧所受应力为38.052 MPa。在吊篮离地之前,伸缩臂受到的综合应力急剧增大,在2.5 s时后,达到临界点时的最大应力为117.859 MPa。吊篮离开地面后,伸缩横臂的端部所受到的综合应力减小,在经历了5.5 s以后,应力平衡在88.021 MPa。这个过程中伸缩横臂的最大综合应力比稳定状态提高了33.9%。 表1 吊重突然起升离地时各时间参数Table 1 Time parameter table when hoisting suddenly lifted off the ground 整个系统用从起升到稳定用时大约3.5 s。在系统稳态被破坏时会由于惯性产生一个额外载荷,在系统回归稳定状态的过程中,整个系统又像会弹簧一样呈现波动状态下降到稳定值。在整个过程中端部位移变化较明显,但应力随载荷变化的范围在标准范围之内。 伸缩臂吊重匀速下降后突然制动,对此工况进行瞬态动力学分析。其中t1=2 s,t2=2.1 s,t3=4.6 s,t4=6.6 s。在前期匀速下降阶段,所受载荷量恒定。在2~2.1 s的阶段,伸缩横臂负载瞬间停止运动,伸缩横臂的端部受到极大的冲击力。2.1~4.6 s阶段为伸缩横臂负载从制动过程到逐渐稳定。4.6~6.6 s阶段为伸缩横臂再制动后的稳定过程。载荷随时间的变化曲线如图10所示。 图10 伸缩臂吊重匀速下降制动时载荷-时间关系曲线Fig.10 Load-time curve of telescopic arm when hoisting dropping at constant speed drop with suddenly braking 伸缩臂的端部是发生最大位移的地方,方向为竖直向下,伸缩臂端部时程曲线图如图11所示。 图11 伸缩臂端部时程曲线Fig.11 The time-history curve at the end of telescopic arm 由图11可知,伸缩臂在吊篮匀速下降时伸缩臂端部位移是75.972 mm。在工作过程中突然产生制动状况,其伸缩臂承受冲击载荷,但是随时间变化,载荷逐渐减小,最后达到了稳定的状态。在2.2 s时达到了最大值为84.937 mm,这是伸缩臂承受最大载荷时候的最大位移。经历了3.8 s后伸缩臂端部稳定在75.972 mm。吊篮在匀速下降时受到冲击载荷,结果使得伸缩横臂的最大位移比稳定状态时增多了11.8%。 不考虑应力集中,红色区域为基臂下翼缘受到应力最大的点,发生时间时在2.1 s时,应力达到了102.271 MPa,具体应力云图如图12所示。 图12 基臂下翼缘应力云图Fig.12 Stress cloud diagram at the lower flange of the base arm 伸缩臂的最大应力随着载荷的变化而变化,应力随时间变化如图13所示。 图13 应力-时间曲线Fig.13 Stress-time curve 由图13可知,伸缩横臂的基臂前沿下翼的边缘处在吊篮匀速下降时所受到的综合应力为98.237 MPa。在突然制动的时候,产生的冲击载荷在波动后逐渐减小,最后达到了稳定的状态;与此同时,伸缩横臂的基臂的综合应力在这种情况下突然增大,其中最大值达到102.271 MPa,之后又逐渐变小趋于稳定回到了98.237 MPa。在整个过程中伸缩臂的最大应力比空载时的载荷提高了4.2%。 在系统打破匀速下降的稳定状态时,会由于惯性产生一个额外载荷,在系统回归稳定状态的过程中,整个系统又像会弹簧一样呈现波动状态下降到制动前的值。在整个过程中端部位移变化较明显,但应力随载荷变化的范围在标准范围之内。 吊重匀速下降制动时,由于整个伸缩臂都处于同一弯曲状态,所有伸缩臂看做一个完整的力臂,因此此时伸缩臂的最大综合应力发生在伸缩臂基臂的下翼缘处,然而在吊重突然起升离地时,整个伸缩臂处于空载状态,当重物突然离地时,整个系统稳定状态被打破,二节臂的拖轮与一节臂组成杠杆,一节臂的臂尾顶在二节臂上翼缘,而二节臂与基臂的响应速度相对滞后,因此此时的最大综合应力发生在二节伸缩的上翼缘。 (1)伸缩臂的负载在匀速下降后制动的工况和伸缩臂负载离地起升的瞬间,静载荷和动载荷对结构的冲击比较大,尤其是吊重突然离地起升工况时,其最大应力较静载作用下增大了33.9%,最大位移较静载作用时提高了33.4%。 (2)两种工况下,应力和端部位移的曲线走向形式基本一致,在冲击载荷产生后都呈现波动状态,最后都稳定在相近值,由于在突然起升离地时用的时间比在匀速下降过程中用的时间短,所以在起升离地过程中因速度变化所产生的冲击载较大,对擦窗机伸缩臂的冲击作用更加激烈。 (3)吊重突然起升离地时,最大综合应力发生在二节伸缩的上翼缘,吊重匀速下降制动时,伸缩臂的最大综合应力发生在伸缩臂基臂的下翼缘处,因伸缩臂为一个矩形的管,在起升是上翼缘受拉大于下翼缘受压,而匀速下降制动时恰恰相反,但是在当达到稳定状态时,两种工况的应力分布情况基本一致。 因此在擦窗机设计时应充分考虑冲击载荷的作用,在特殊工况下应控制速度变化时加速度的大小。
2.4 其余参数的设定
3 瞬态动力学求解
3.1 伸缩臂结构对应吊重突然起升离地时动态响应


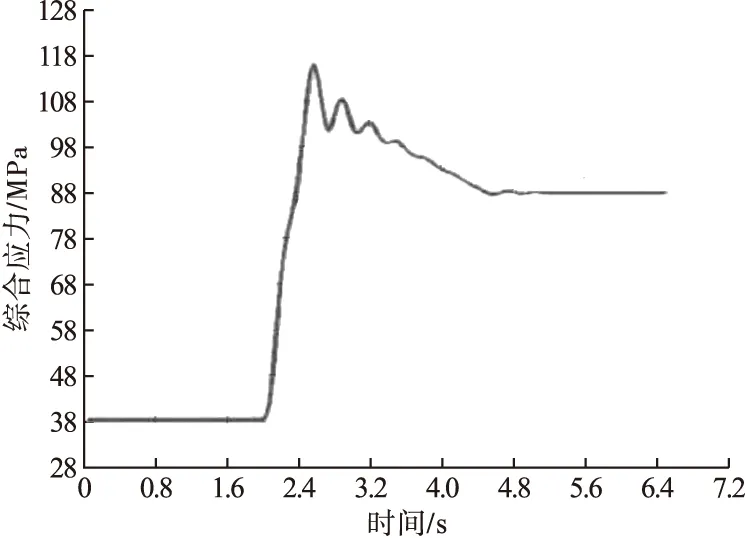
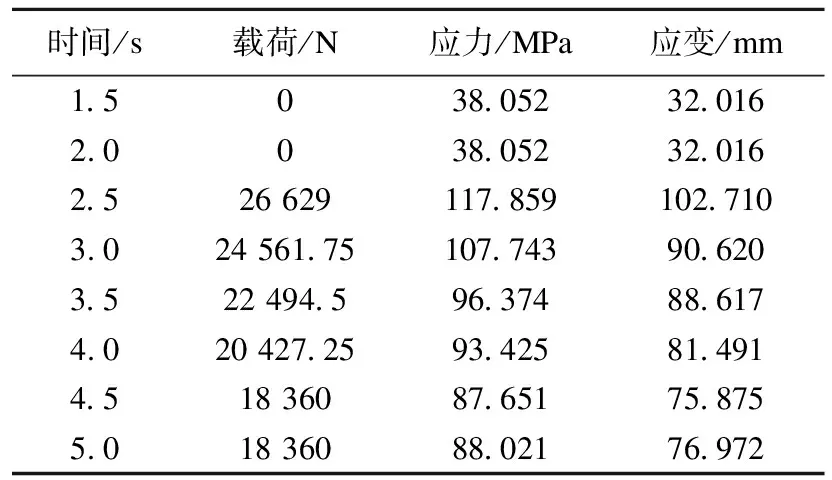
3.2 吊重匀速下降制动时伸缩臂结构的动态特性响应

3.3 两种工况下最大应发生区域
4 结 论

