高速短初级直线感应电动机等效电路模型及时变参数辨识
韩正清,许金,芮万智,朱俊杰,吴延好
(海军工程大学 舰船综合电力技术国防科技重点实验室,武汉 430032)
0 引 言
直线感应电机(linear induction motor,LIM)是一种可以直接产生直线运动的机电能量转换装置,广泛应用于轨道交通[1]、直线电梯以及军事电磁发射领域[2-3]。但直线电机存在固有的边端效应,使得电机性能分析较为复杂。
直线电机与普通旋转感应电机的根本区别在于由于铁心开断引起的边端效应。边端效应主要分为横向边端效应和纵向边端效应。其中横向边端效应可以通过电机结构设计进行避免,并且对于次级宽度大于初级的直线电机,横向边端效应不明显,可忽略[4]。文献[5]提出了一种格栅型次级作为直线电机新型拓扑结构,验证了该拓扑可以削弱横向边端效应,增大电机电磁推力。静态纵向边端效应是指直线电机存在固有的阻抗不对称特性,文献[6]指出通过增加电机极数,可减小电机阻抗的不对称度,当极数大于等于6时便可忽略静态纵向边端效应影响。但对于分段供电电机[7-9],由于存在未通电段,其必须考虑静态纵向边端效应。
动态纵向边端效应是由于LIM初级和次级相对运动而引起的电瞬态现象。LIM初级入端和出端会在次级导电层上感应边端涡流,使得电机电磁气隙发生畸变。动态纵向边端效应研究是LIM最热门的话题,重点对场分析、等效电路模型、参数辨识及控制策略等方面展开研究。文献[4]基于一维场理论推导了动态纵向边端效应影响下LIM磁场畸变特性,指出动态纵向边端效应随着速度增加而更加显著。文献[10-11]推导了考虑边端效应下LIM电磁参数修正系数,并构建了LIM等效电路模型,其结构类似于传统T型等效电路模型。该模型可以用于LIM稳态和动态性能分析,并在LIM控制中得到应用[12]。由于模型修正系数是基于场理论计算得到,与电机结构参数和运行工况相关,公式较为复杂且推导时附有大量假设条件。Duncun[13]同样基于T型等效电路模型,推导了更为简便且易于理解的等效电路模型。Duncun指出,根据磁链守恒原则,在LIM的入端处,新的次级部分会迅速感应出与励磁电流大小相等,相位相差180°的次级涡流,使得气隙磁势几乎为零,通过在传统的T型等效电路模型的励磁支路基础上并联一个电感,等效刻画动态纵向边端效应使得励磁磁势减小的特性,提出了f(Q)模型。该模型由于表达式简便,在电机控制中应用尤为广泛。后来的学者在f(Q)模型基础上考虑了次级漏感影响,提出了f(A)模型[14]以及考虑转差率的s_f(Q)[15]模型。但对模型参数的修正上都没有考虑铁心饱和的影响。
对于高功率大推力密度LIM,电机铁心往往处于饱和状态。因此,由于动态边端效应和铁心饱和影响,在整个动态运行过程中,电机等效电磁参数是一直变化。目前传统模型不能对多因素耦合下电机等效电磁参数准确修正。对于参数辨识,有在线和离线辨识两类方法。第一类是构造合适的状态观测器在线辨识电机参数,如全阶或者降阶观测器[16]、模型预测[17]、扩展卡尔曼滤波[18]、模型参考自适应[19]等。如文献[19]提出自适应在线参数辨识的反馈线性控制。文献[20]为了解决永磁同步电机多参数在线辨识存在欠秩、相互耦合的问题,提出了分步辨识策略,即先用高频正弦电压注入法,辨识d、q轴电感,再通过最小二乘法辨识电阻和磁链。但高速LIM工作时间短,运行速度高,而在线参数辨识方法有计算量大、精度不高、实时性不强等问题。文献[21]利用逆变器依次向直线感应电机中通入单相直流电压、单相交流高频电压和单相交流低频电压来获得等效电路中的静止条件各个参数,并评估了死区效应对参数表示的影响。文献[22]利用最小二乘法分别基于实测电磁推力频率曲线和端口电压对静止条件下直线感应电机在不同饱和工况下的激磁电感和定子漏感进行辨识。另外由于静态纵向边端效应影响,直线感应电机阻抗不再是循环对称矩阵,文献[23]定义基波正序阻抗概念,并基于正序阻抗和稳态T型等效电路,通过静态测试方法辨识了等效电路的对称参数。传统基于空载和堵驻试验的离线参数辨识方法[21-26]不能解决随工况变化的参数辨识问题。本文基于电磁场有限元软件,采用响应面分析法解决多因素耦合下的时变参数辨识问题,构建精确的高速LIM等效电路模型。搭建了实验平台,开展静态堵驻和动态实验,验证时变参数辨识的精确性。
1 边端效应和铁心饱和对推力性能影响
1.1 有限元模型
如果LIM全模型的3维有限元瞬态场可以被分析,有限元计算结果可以最大程度逼近实际。但实际上,3维瞬态场对计算器配置需求非常高。而对于硅钢片次级,可以采用文献[27]中kRN的次级电阻修正系数来考虑电机三维特性。所以,本文只需建立2维有限元瞬态场模型即可考虑动态纵向边端效应,通过修正次级材料电导率来等效次级电阻修正系数。图1为2维有限元模型,表1是电机电磁结构参数。

图1 2维有限元模型Fig.1 2D finite element model

表1 电机电磁结构参数Table 1 Electromagnetic structure parameters of motors
1.2 动态纵向边端效应和饱和对推力影响

(1)
(2)
从表达式中可以看出,由于边端涡流的影响,磁场分布的正弦性并不是很理想,其在空间位置上分布特性除了与电机结构参数相关外,还与运动速度、转差率以及初级电流相关。
图2给出了峰值电流1 000 A时,速度分别为10 m/s、20 m/s、30 m/s、40 m/s时,不同转差频率下电机推力有限元计算曲线。从图2中可以看出,电机最大输出推力随着速度增加而减小。另外,最大输出推力对应的转差频率点随着速度增加而增加,如10 m/s时为8 Hz,40 m/s时为12 Hz。

图2 电流幅值1 000 A时,不同工况下的电机输出推力Fig.2 When the current amplitude is 1 000 A, the motor output thrust under different working conditions
图3给出了电流1 000~10 000 A,速度为40 m/s,转差频率10 Hz时的推力曲线。从图3中可以看出,随着初级电流增加,电机饱和效应显著,此时推力与电流的平方不是一个简单的线性关系。

图3 不同电流等级下的电磁力Fig.3 Electromagnetic force at different current levels
图4是速度5 m/s,40 m/s时,峰值电流10 000 A,转差频率10 Hz时的铁心磁密云图,可以看出,40 m/s工况时铁心的平均磁密小于5 m/s工况,可以说明即使电机电流相同,运行转差频率相同,速度不同时,两个工况下的电机饱和效应还是存在很大区别的,因此动态纵向边端效应也会对电机饱和特性产生影响。所以当动态纵向边端效应和饱和同时作用时,电机电磁气隙内磁场分布特性更加复杂,这给理论计算电机电磁参数带来很大的问题。而电机电磁参数的准确性直接影响到电机性能计算和控制效果。下面将针对多变量工况下直线感应电机改进等效电路模型和时变参数辨识方法展开介绍。
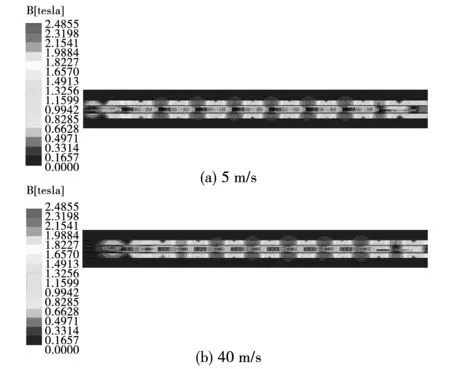
图4 磁密云图Fig.4 Magnetic field density nephogram
2 改进等效电路模型及时变参数辨识
2.1 改进等效电路模型
在文献[11]提出的等效电路结构基础上,本文提出多变量工况下直线感应电机改进等效电路模型如图5,其中f(is,v,fs)、g(is,v,fs)分别是激磁电感和次级电阻的修正系数,其是一个关于初级电流,速度和转差频率的关系式。当电机处于静止状态下,且铁心未饱和时,f(is,v,fs)=1。g(is,v,fs) =1。图5中Rs、Ls、Lm0、Llr、Rr0分别是初级电阻、初级漏感、激磁电感初始值、次级漏感和次级电阻初始值,见表2。

表2 静止状态下电机线性参数Table 2 Linear parameters of motor in static state

图5 直线感应电机改进等效电路模型Fig.5 Improved equivalent circuit model of linear induction motor
对于某稳态工况,基于推力和感应电势等效,利用式(3)、式(4)可以计算出稳态工况下的激磁电感和次级电阻的修正系数。由于边端效应影响,LIM存在不对称特性,导致各相感应电势不是严格对称。为此,式中F为输出推力的平均值,τ为极距,e、s分别为供电角频率和转差角频率,为基于序量变换公式(5)得到的感应电势正序分量,a=ej120°。
(3)
(4)
(5)
2.2 时变参数辨识
通过计算电机稳态工况下的等效电磁参数,结合响应面分析方法(RSM)来辨识不同工况下电机时变参数。
RSM可用于分析响应函数受多个设计变量影响的问题,其目的是优化该响应。在这种方法中,响应y作为设计变量的函数可以通过实验来提供。在RSM中,响应y是未知的。变量与响应y之间的关系可以用一个数学模型来描述,称为回归模型。为了建立回归模型,可以使用一阶或二阶模型。本文采用二阶模型对响应面进行建模,如式(6)。
(6)
其中:y为响应;β0,βi,βii,βij是回归系数;βii是变量本身平方的系数;βij是两个不同变量乘积项系数。x为设计变量,n为设计变量个数,ε为随机误差。
为了计算式(6)中的回归系数,需要以n个设计变量作为实验因素进行实验设计,共进行m次实验。令Y=[y1,y2,…,ym]T是一个m维的列向量。令
矩阵X是一个m行r+1列的矩阵,第1行中的φ11,…,φ1r分别表示的是第一次实验设计中,设计变量数值,设计变量本身平方及两个不同设计变量乘积项的数值。根据m次实验设计,则可以得到矩阵X。令β是一个r+1维的列向量,列向量中系数由式(6)中回归系数组成。
则根据m次实验设计,可以写成:
Y=Xβ+ε。
(7)

(8)
为了创建响应面,需要计算大量实验样本。本文采用拉丁超立方试验在优化参数范围内抽取典型样本,其中优化参数的变化范围为电流1 000~10 000 A,速度0~50 m/s,转差频率5~20 Hz。用典型样本的计算值估计响应面函数。本文共抽取了15组典型样本,为节省空间,表3给出了4组设计变量的运行结果及其对应的响应结果。

表3 典型设计变量运行结果及其对应的响应Table 3 Operation results of typical design variables and their corresponding responses
再而,根据式(8),从而得到二阶响应面函数如下,式中x1、x2、x3分别表示的是电流(kA)、速度(m/s)及转差频率(Hz)。

(9)

(10)
使用决定系数评价响应面模型的精度,式(9)、式(10)决定系数分别是0.987,0.999,说明模型拟合精度高。
3 参数计算结果验证
为验证本文所提出的时变参数计算精度,基于提出的改进等效电路模型展开电机性能计算,并与实验值进行对比,从而验证本文所提出的时变参数辨识方法的准确性。图6为实验样机。开展样机实验,逆变器根据电压指令将直流侧电压转换成相应的交流电压,传输至LIM。利用高精度电流霍尔传感器、高精度高压探头以及高采样频率数据采集系统来采集LIM端口电流及电压波形。利用拉力传感器测量LIM输出电磁力。

图6 实验样机Fig.6 Experimental prototype
3.1 静态堵驻实验
将动子固定,开展峰值电流等级8 000 A时不同频率下静态堵驻实验。基于改进的等效电路模型,可以理论计算出各工况下的电机推力,两者结果对比如图7,误差不超过4.1%。

图7 推力曲线Fig.7 Thrust curve
3.2 动态实验
由于动子运动过程中,电机推力难以直接测量。通过提取实验端口电压、电流数据,计算电机端口基波正序阻抗,计算方法可参照文献。同样,基于改进的等效电路模型,可以计算出电机端口基波正序阻抗,对比结果如图8、图9。图8是速度为35 m/s,峰值电流8 000 A时,电机端口基波正序阻抗实部、虚部随转差频率变化时计算值与实验值对比曲线,阻抗实部误差不超过4.3%,阻抗虚部误差不超过4.7%。

图8 电机端口基波正序阻抗随转差频率变化曲线Fig.8 Variation curve of fundamental positive sequence impedance of motor port with slip frequency
图9是转差频率为10 Hz时,峰值电流8 000 A时,电机端口基波正序阻抗实部、虚部随速度变化曲线。为了比较,图中还画出了传统经典的f(Q)模型[13]计算曲线,从图中可以看出,本文模型计算值与实验值吻合更好,两者阻抗实部误差不超过4.5%,阻抗虚部误差不超过4.4%。

图9 电机端口基波正序阻抗随速度变化曲线Fig.9 Variation curve of fundamental positive sequence impedance of motor port with speed
通过静态推力和动态运行时电机端口基波正序阻抗的计算值与实验值对比,验证了本文改进等效电路模型和时变参数辨识的准确性。
4 结 论
由于强动态纵向边端效应和高饱和特性的影响,在动子高速运动过程中,电机电磁参数在动态变化。本文分析了运动速度、转差率以及初级电流对电机推力性能影响,说明了导致电机参数时变的影响因素,构建了改进等效电路模型。基于推力和感应电势的有限元计算结果,采用响应面分析法解决多因素耦合下的时变参数辨识问题。开展样机静态堵驻和动态运行实验,实验结果表明:推力计算值与实测值误差不超过4.1%,端口基波正序阻抗的实部、虚部计算值与实测值误差不超过4.7%,验证了改进等效电路模型和时变参数辨识的准确性。

