基于博弈论的用户需求驱动模块划分*

丁翔宇,刘 丹

(贵州大学现代制造技术教育部重点实验室，贵阳 550025)

0 引言

为适应消费者的个性化定制需求，产品的模块化设计提供了一种适用度较高的产品设计框架，合理的模块划分可使设计过程更能满足多样化的功能需求，同时降低设计成本，缩短设计周期等。

目前国内外围绕着机械产品的模块划分方法已进行了大量研究。龚京忠等[1]建立了通过以图分割进行模块划分的方法；谌炎辉等[2]建立了一种以最大最小思想为指导的模块划分方法；吕健等[3]建立了基于凝聚层次聚类的模块划分方法；姜芊芊[4]提出了结合IFWA和FCM的模块划分算法。

现有的模块划分方法有两个亟待解决的问题：第一是大多基于产品结构的相互关联性进行模块划分，没有从用户需求的实际出发；第二是定性指标定量化的方法主观性太强，误差太大导致最后的划分方案可信度降低。

博弈论的相关模型可以用来解决整体利益分配和多目标选择的问题，事实上博弈论在工程领域已有一定的应用。侯秋霞等[5]利用Stackelberg 博弈模型建立了一个由通用化模块供应商和制造商组成的大规模定制供应链模型；王浩伦[6]提出并构建了基于非合作博弈的产品族策略选择模型；Albrecht J等[7]将夏普利值分解技术运用在解决连续时间下的二氧化碳排放问题;赖苹等[8]探究了模糊动态Sharpley Value在流域水污染治理效用分配上的应用；Jing L等[9]以形态矩阵为基础，运用模糊聚类，非合作博弈和合作博弈的方法设计一种产品概念方案的决策方法。

本文提出一种从在线评论中获取用户需求，以合作博弈的思想建立一套从用户实际需求出发来指导产品设计方案的创新模块划分方法和方案评价体系，此方法不依赖专家打分等主观性过强的设计方法，希望能为现有的模块化设计提供一种新的思路。

1 基于合作博弈的产品模块划分

本文从网络评论信息中提取用户需求，建立设计参数-用户需求-产品部件的映射矩阵；然后运用核与Sharpley Value等博弈论理论设计一套权重分配方案，将提取到的用户需求量化数据分配到各个部件中，而不同部件关于所有设计参数量化指标的比值即为部件间的关联度，这样组成的关联矩阵是直接从用户数据中获取的，更能体现用户对产品的期望；接着通过改进模糊聚类算法求出动态聚类树，得到模块划分方案；为了在不同的模块划分方案之间优中选优，运用核仁解和纳什均衡等博弈论理论设计一套评价体系，得到最符合用户要求的最优划分方案。

算法流程如图1所示。

图1 基于博弈论的模块划分算法流程图

1.1 建立F-CN-P关系矩阵M1

网络评论信息中有大量非结构或半结构的信息，需要经过筛选有用信息组，对信息进行结构化处理，最终得到产品的设计参数集合F={F1,F2,…,Fi}，用户需求集合CN={CN11…CN1m1…CNi1…CNimi}和产品的部件集合P={P1,P2,…,Pn}，并建立F-CN-P的映射矩阵M1：

p1p2…pn

其中，Wimin为用户需求和部件的关联系数，即在功能块Fi下第mi个用户需求CNimi的部件Pn的权重值，Wijk的取值差异性用以表现部件对于实现用户需求CNij上重要性的差别，取值规则如下：

先假定所有相关部件Wijk均为1(当Pk对CNij的实现无关联时，Wijk=0)，将所有部件两两进行比较，若在用户需求CNij实现上，Pk1比Pk2更重要，则令Wijk1=2，由此确定关联系数为2的全体部件，同理再确定关联系数为3的全体部件，直到所有最高关联系数的部件相互之间不存在重要度的显著差异。由此确定对于特定用户需求CNij的所有部件的关联系数Wijk：

(1)

由于主观判断的不确定性，不同的关联系数Wijk形成了不同的映射矩阵M1，即为策略集(Tactics)T=(T1,T2,…,Tt)。而不同的策略Tj形成了不同的模块划分方案。

1.2 基于博弈论的模块划分方法

1.2.1 理论框架

以用户需求CNij的关键词词频作为合作博弈中的整体效用函数v(N)，结构部件Pk=(k=1,2,…,n)作为参与博弈的各个参与者(Player)，为了将量化数据合理地分配给各个部件，就必须使得这个权重分配方案(Imputation)x={δP1,δP2…δPn}是“稳定”的，即任意联盟S的效益需满足超可加性：

∀Pk∈S,v(S)≥v(S{Pk})

其中，v(S{Pk})为联盟S除去参与者Pk的效用。

1.2.2 确定效用分配函数v(S)

根据合作博弈中的核(Corel)的概念[10]，按照如下设计原则确定效用函数v(S)：

(2)

(3)

(4)

其中，WS表示联盟S的关联系数总和，WN表示联盟N的关联系数总和,|S|表示联盟S的参与者个数。

1.2.3 确定量化指标矩阵M2

运用Sharpley值的计算方法，得到每个参与者Pk的分配的效益值δ(Pk)：

其中，π(N)为大联盟N所有的排列，σ为其中一种排列方式，mσ(Pk)为边际效用向量；由此确定的权重分配方案(Imputation)x是“稳定”的，不存在任何一个子联盟S可以对分配x进行改善。

对每一个用户需求CNij的词频数据进行权重分配，得到的量化指标也即表示部件Pk在某个特定用户需求CNij上的量化得分数值，获得的量化指标矩阵M2如下：

p1p2…pn

1.2.4 确定模糊相似矩阵M3

为得到每个部件在各个设计参数上的属性值，按照公式(5)得到部件P的设计参数属性表，如表1所示。

(5)

其中，δin为部件Pn在功能Fi上的量化数据。

通过公式(6)，按照两个部件间在不同功能块上量化得分的比值得到部件的相对关联度γij，得到模糊相似矩阵M3：

(6)

P1P2P3…Pn

1.2.5 建立模糊矩阵并确定模块划分方案

M3模糊相似矩阵具有自反性和对称性而不具有传递性，为此运用求解传递闭包的方法，将相似矩阵M3转化为等价矩阵。

根据公式(7)对相似矩阵进行迭代的逻辑运算，直到第一次出现Rk∘Rk=Rk停止迭代,并且Rk即为所求的等价矩阵[11]。

(7)

其中，∨为逻辑加，取最大值；∧为逻辑减，取最小值。

得到Rk等价矩阵之后，以不同阈值λ：1→0求得不同的截矩阵，生成动态聚类树。

1.3 建立划分方案评价体系

不同的策略Tj可以确定不同的模块划分方案，要从这些结果中选取合适的最优方案需要建立一个科学合理的评价体系。

根据合作博弈中超额(excess)和核仁解(nucleolus)等概念，设计对划分结果的评价体系：

∑v(S)与最大量化指标值v(N)的差值即为用户“抱怨”程度(不满意度)见公式(8)：

(8)

表2 T-F不满意度值

续表

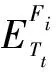
再根据公式(9)对不满意度进行归一化处理，得到不满意度比值exy：

(9)

F1F2F3…Fi

1.4 确定最优模块划分方案

根据核仁解(nucleolus)理论，在各个模块划分方案中的最大不满意度比值中找到最小的那个方案即为核仁解策略Tncl，但这种择优策略不能满足整体的不满意度值最小，然后求出整体的抱怨指数最小的集合，这样就筛选出几个最优方案，再通过比较不满意度数值的大小，求得的最优方案则是整体和个体都最优的模块划分方案。

步骤1： 确定核仁解策略Tncl

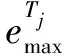
(10)

(11)

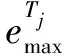
(12)

为了得到最优方案，需要从δ(1)中继续寻找博弈的合理解，再从“第二位”最大不满意度比值emin(2)中寻找最优方案，知这个过程可能一直持续下去，定义公式(13)为第k大的不满意度比值集合为δ(k):

(13)

Schmeidler[12]证明了这种迭代过程最终会“收敛”于一点，即“核仁”；所以，必定会得到一个核仁解策略Tncl。

步骤2： 确定最小总体抱怨指数集合

根据纳什均衡的思想，最优方案应使得每个参与者达到帕累托最优，即当一个参与者的决策确定后，其它参与者的决策也相应确定。按照这个思路，确定每个策略的总体抱怨指数ej，取最小值为min(e)，易知达到这个最小值的策略Tj可能不唯一，将达到最小值min(e)的策略集合设为A(e):

(14)

(15)

步骤3： 确定是Tncl否在A(E)中

若Tncl∈A(e)，则Tncl为选取的最优策略，其对应的划分结果即为模块划分的方案；

若Tncl∉A(e)，则根据公式(16)计算A(e)和Tncl的总体不满意度值Ej,数值最小的则为最优模块划分方案，对应的策略则为最佳策略。

(16)

2 实例验证

2.1 确定关系矩阵M1

选取消费类家电产品作为研究对象，使用Python编程语言对电商平台中的洗衣机的评论信息进行提取，采用开源的中文分词方法对选取的超过11 000条评论信息进行关键词提取，筛选并统计关键词词频，并转化为结构化的用户需求，结果如表3所示。

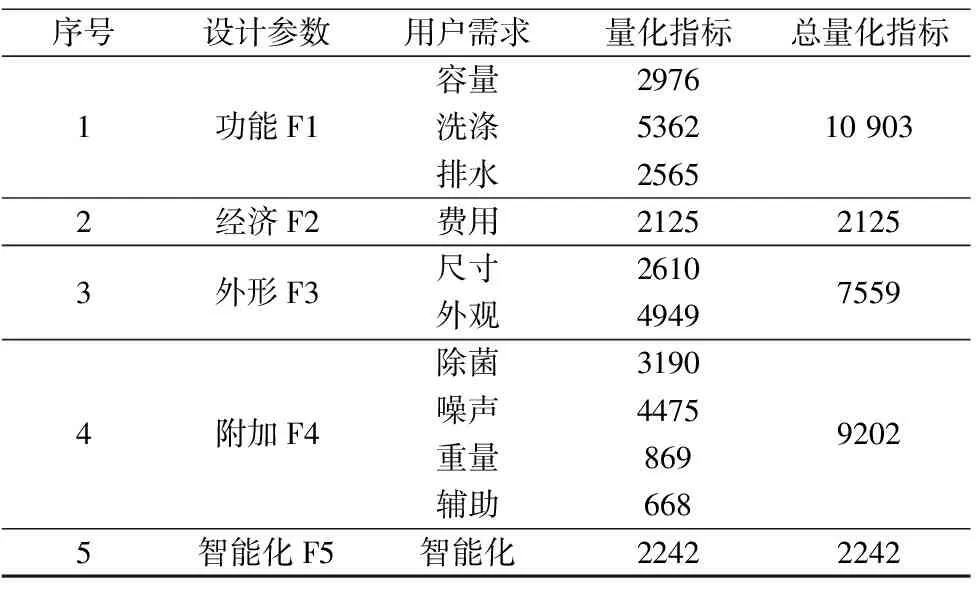
表3 F-CN量化指标表

洗衣机具有数百个零件，为简化计算将零件进一步组成部件，如图2、图3所示。

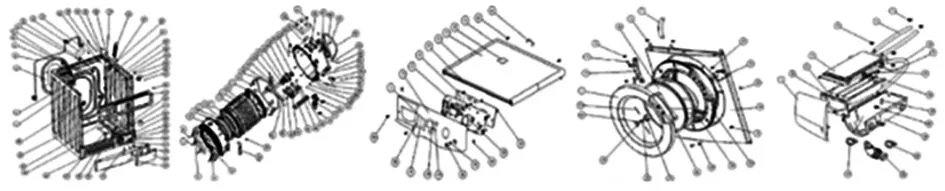
图2 洗衣机零件爆炸图

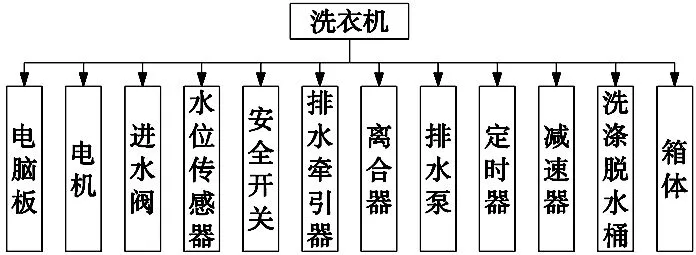
图3 洗衣机主要部件图

建立策略集T={T1，T2，T3}各自的关系矩阵M1，见表4～表6。

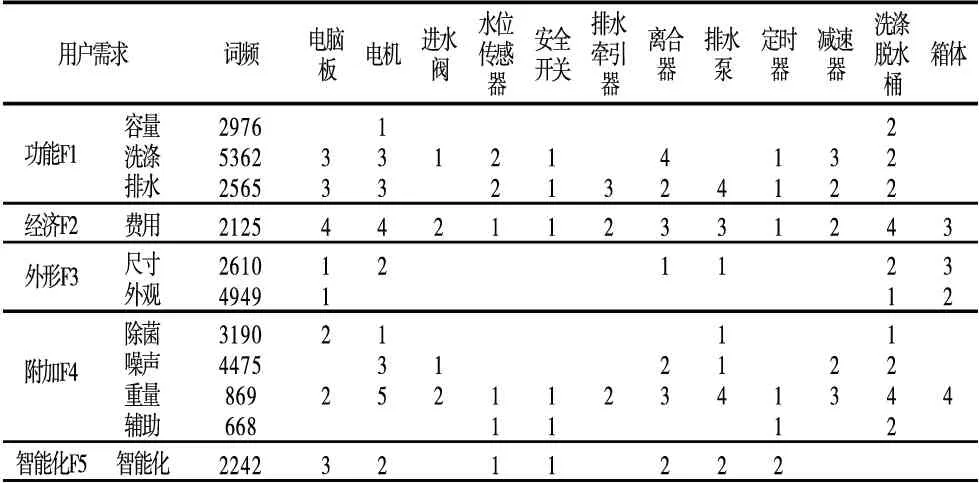
表4 T1对应关系矩阵M1

表5 T2对应关系矩阵M1

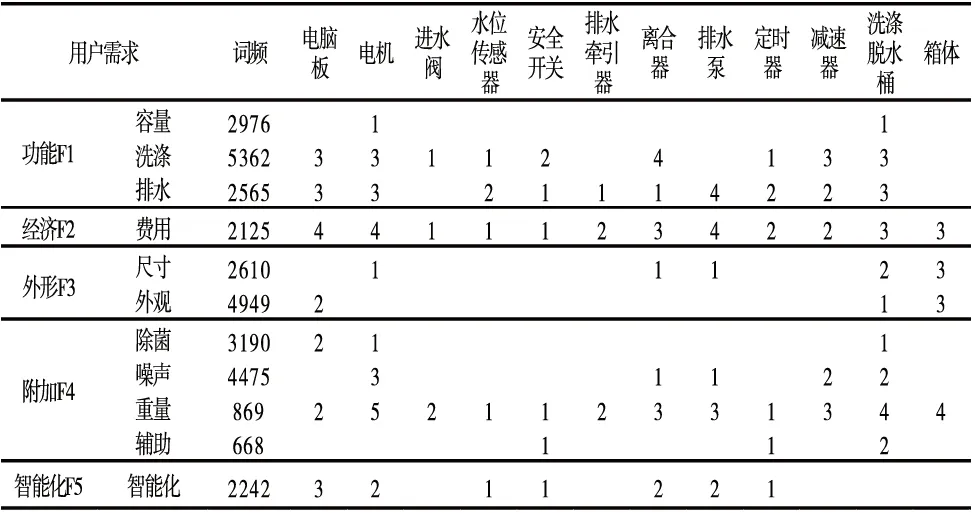
表6 T3对应关系矩阵M1

2.2 确定量化指标矩阵M2

以策略T3为例，计算得到策略T3的量化指标矩阵M2，见表7。

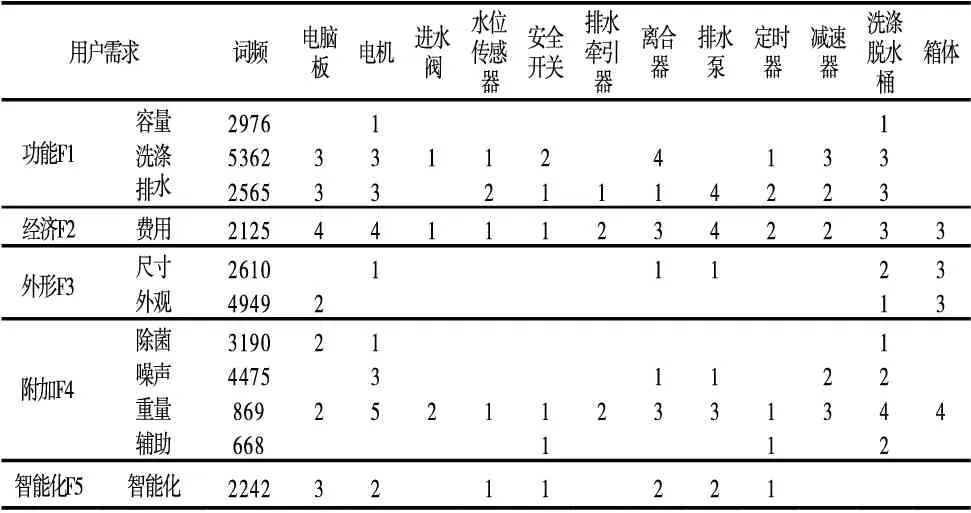
表7 T3对应量化指标矩阵M2

2.3 确定模块划分方案

根据式(6)、式(7)，得到关于T3的截矩阵Rλ，见表8。

表8 T3对应截矩阵矩阵Rλ

得到的策略集T={T1,T2,T3}的模块划分动态聚类树如图4～图6所示。

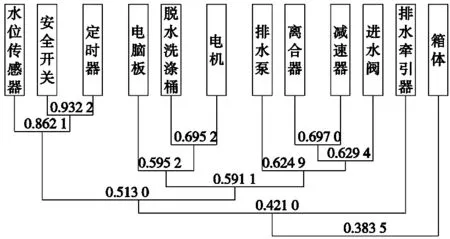
图4 T1对应模块划分动态聚类树

图5 T2对应模块划分动态聚类树

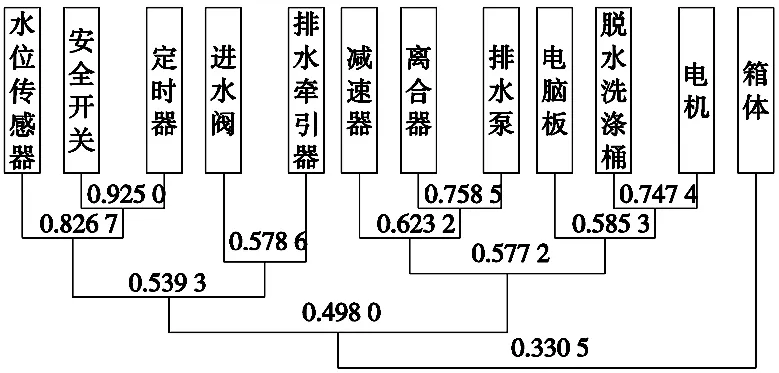
图6 T3对应模块划分动态聚类树

根据3个动态聚类树，按照λ=0.591 1求出策略T1的模块划分方案，按照λ=0.560 3求出策略T2的模块划分方案，按照λ=0.577 2求出策略T3的模块划分方案,如表9所示。表9中：1为电脑板，2为电机，3为进水阀，4为水位传感器，5为安全开关，6为排水牵引器，7为离合器，8为排水泵，9为定时器，10为减速器，11为脱水洗涤桶，12为箱体。

表9 策略对应模块划分方案

2.4 确定最优模块划分方案

根据式(8)、式(9)、式(14)，得到拓展决策矩阵M4，并确定最小总体抱怨指数集合A(e)：

表10 拓展决策矩阵M4

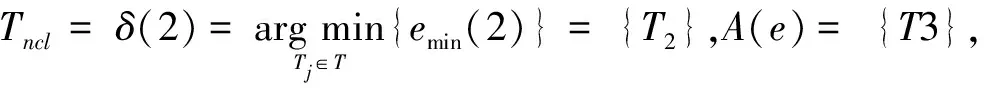
表11 总体不满意度

于是得到了最优模块划分方案T3={(水位传感器，安全开关，定时器)，(进水阀，排水牵引器)，(减速器，离合器，排水泵)，(电脑板，脱水洗涤桶，电机)(箱体)}。

3 总结

本文运用博弈论设计了一套从用户需求出发的改进模块划分方法及其评价体系，用消费类机电产品中的洗衣机作为范例，验证该方法的可行性和有效性。需要指出的是，由于本文提供的方法是直接从用户需求中获取数据，可能会存在用户需求的表达和实际生产之间出现矛盾的问题，本文旨在提供了一种从用户需求出发来指导生产的依靠数据驱动的客观的模块化设计的新思路、新方法，架设用户和生产者之间沟通的桥梁，实现从用户中来到用户中去的设计闭环。当然文章中还有一些需要改进的地方，比如联盟效用v(S)的确定能否不用公式确定，而是更好地收集用户的反馈来获得量化数据；又比如关联系数Wijk以及策略T的确定是否能摆脱专家经验，最大程度减少主观性判断对结果的影响。