典型几何特征在机测量评定算法研究*
丁文政,王明涛,陈 勇,卞 荣
(南京工程学院工业中心,南京 211167)
0 引言
制造业中,目前仍大量使用由手动量仪(如千分尺、百分表、游标卡尺和深度尺等),或三坐标测量机等仪器设备构成的离线检测单元,其测量效率低、人力成本高、测量结果反馈不及时,无法满足智能制造高效检测反馈和加工补偿的需求[1]。随着智能制造的发展,在机测量开始成为高端数控机床的标配。在机测量以数控机床为基础,附以硬件(高精度机床测头)和软件(测量程序、测量评定算法),实现工件加工过程中或加工完成后,直接在机床上进行测量,避免多次装夹引起的误差,减少辅助工时,降低成本,提高效率[2]。
数控机床在机测量的硬件有接触式和非接触式两种。机器视觉、激光成像和CT成像等非接触式测量可以短时间内获取大量二维、三维工件几何特征数据,但成本高、可靠性低[3-5]。接触式测量采用触发式测头等设备,能可靠地获取工件轮廓几何特征信息[6]。当前硬件测量数据已具有较高的精度,但需要按照工件几何特征的相关概念进行数据处理,才能得到几何特征的标注尺寸,因而相应的评定算法是在机测量应用的关键。
最小二乘法是工件几何特征评定中常用的方法[7-8]。为了提高最小二乘法的拟合精度,在直线评定中开发了整体最小二乘法[9];在圆弧评定中开发了基于圆心约束的最小二乘圆拟合法[10-11];在齿轮工件的测量中,开发了基于半径差约束的最小二乘法[12-13]。
但在复杂工件轮廓的在机测量中,各种几何特征转接频繁,单个几何特征数据量小,转接处数据受到噪声的干扰较大,最小二乘法的直接应用受到限制,难点在于复杂工件轮廓特征的辨识和特征点的提取。为此,本文设计了特征辨识和滤波算法,通过对测量数据进行几何特征的滤波,将复杂工件轮廓数据分解成水平直线段、倾斜直线段和圆弧段等典型几何特征,从而防止不同几何特征之间的误差累积,最终实现复杂工件轮廓几何特征的准确评定。
1 测量原理与算法模型
测量评定算法基于数控加工中心在机测量系统进行研究,系统硬件为雷尼绍OMP600高精度测头,二维轮廓的测量误差为±0.25 μm;运动部件包括机床主轴和进给轴;软件基于西门子840D数控系统,通过OPCUA协议与工作站进行通讯。数控系统读取在机测量程序后,控制机床各轴运动,当测头探针接触到被测工件表面时,传感器感受到被测表面的几何变化,从而触发信号并通过红外传输给接收器,接收器将信号转变成测量数据存储到工作站数据库中。针对测量得到的X-Y二维数据,设计开发特征辨识算法、特征滤波算法、水平直线段、倾斜直线段和圆弧段几何特征评定算法。
1.1 特征辨识算法
由于测头测量起始位置不固定,工件安装位置误差等原因,导致即使同一工件,多次测量的数据变化也很大。为了准确辨识工件几何特征,开发了特征辨识算法。该算法将工件平面轮廓数据,按照水平直线段、倾斜直线段和圆弧段三种典型几何形状的理想特征进行辨识,方法如下:
(1)水平直线段:Y轴数据无变化,斜率为0且斜率变化率为0的一段区域;
(2)倾斜直线段:Y轴数据逐渐变化,斜率不为0且斜率变化率为0,线段转接处的斜率变化率突变;
(3)圆弧段:斜率变化率是连续平滑的一段不为0的区域,转接相切处斜率变化率连续,不相切则为无穷大。
1.2 特征滤波算法
如图1所示工件轮廓,理想状况下,轮廓曲线是平滑的,但由于机床测头存在探针沾污、探针缺陷、扫描位置不准等问题,检测到的轮廓曲线呈现出图中粗糙不平的情况。因此,直接用相邻两点的斜率和斜率变化率来辨识几何特征,其中的特征很可能会被测量数据误差淹没。特征滤波算法不以相邻两点直接求取斜率和斜率变化率,而是采样一段数据进行最小二乘直线拟合,求取该段数据斜率和斜率变化率。
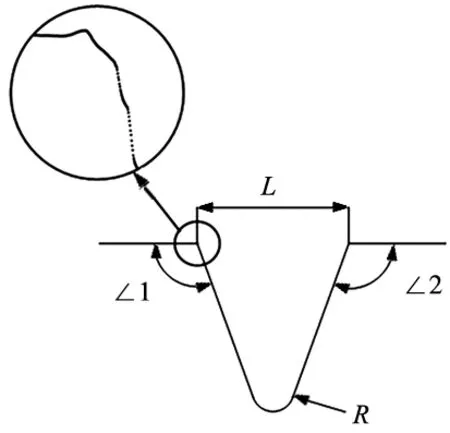
图1 工件1轮廓示意图
图2为数据段采样流程图。其中采样范围控制是关键,范围既要够大,使得拟合误差覆盖过数据噪声;但又不能太大,否则可能会覆盖掉几何特征转接处的信息,这就需要动态控制采样范围。具体方法是:当拟合方差变大时,减小下次的采样范围和步长,采用反比函数,将变化率和方差乘以比例系数以及加幂数来调节,缩小后的采样范围会得到较小的方差,使得在转接处的数据不会因针对方差的滤波而被过滤掉;当方差过大,或者拟合直线不在阈值范围,则判断为匹配失败,下次采样继续在原处,如果在原处再次匹配失败,则跳过该采样段。
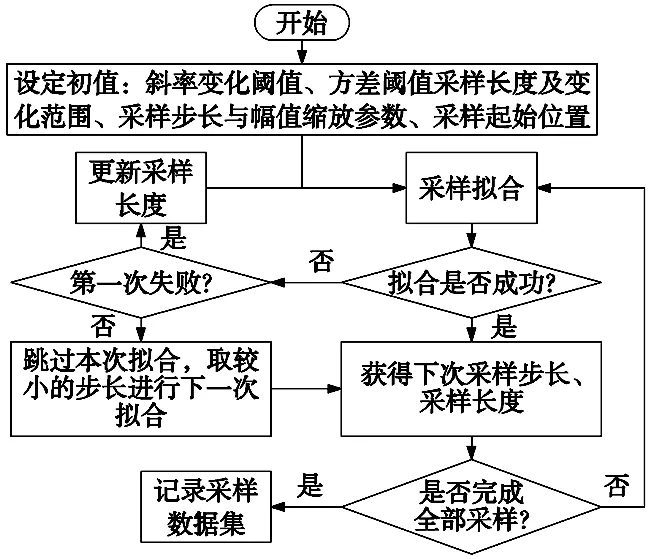
图2 数据段采样流程图
1.3 水平直线段特征评定算法
通过特征滤波,提取出水平直线段数据后,采用垂直偏差最小二乘法拟合,来进行直线段几何特征评定。
直线表达式为:
ax+by+c=0
(1)
令所有N个点(xn,yn)到线的距离方差最小,n=1,2,3,…,N,即求误差平方和J最小时的a、b、c,其中
(2)
用拉格朗日乘数法,令a2+b2=1,得到(ayn+byn+c)2+λ(a2+b2-1),再对a、b、c分别求导,当导数等于0得出:
(3)
(4)
(5)
求解式(3)~式(5)得a、b、c。
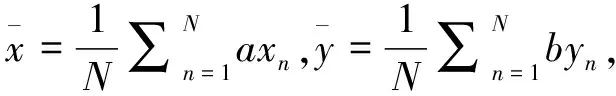
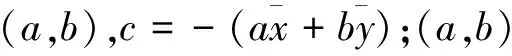
1.4 倾斜直线段的特征评定算法
如图3所示的斜直线之间存在角度约束,由式(5)可知,当直线斜率被约束,方差最小时,直线必然经过数据点云的中心。分别计算出与L1、L2两簇数据点云中心,然后计算a、b。
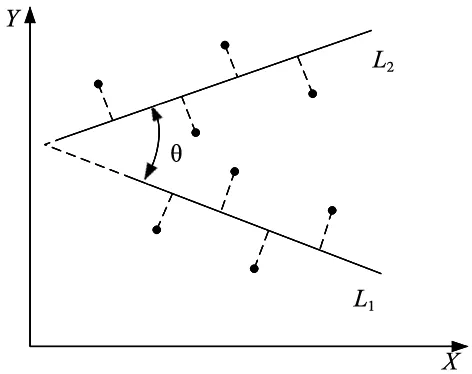
图3 角度约束的斜线段示意图
设直线L1、L2夹角为θ,直线L1斜率k1=a/b,分别计算出L1的A1、L2的A2,再计算得出新的A,如式(6)所示:
(6)
由A可得一组a、b,从而得到k1=a/b就是L1的斜率,L1逆时针旋转角θ得到L2。
该算法可拓展到多条线段的角度约束,如式(7)所示:
A=A1+M(-θ2)A2M(θ2)+…+M(-θn)AnM(θn)
(7)
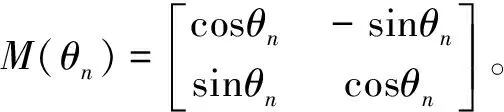
1.5 圆弧段的特征评定算法
通过特征滤波,提取出圆弧段数据后,采用最小二乘圆拟合,来进行圆弧段几何特征评定。
圆弧段的表达式为:
x2+y2+ax+by+c=0
(8)
点到圆心的距离与半径的差为:
xn2+yn2+axn+byn+c
(9)
令所有N个点(xn,yn)到圆心的距离与半径的差最小,即求点到圆心的距离与半径的差的平方和J最小时的a、b、c:
(10)
对J求偏导,并令偏导等于0,可得如下方程:
(11)
求解式(12):
(12)
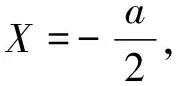
2 实例分析
2.1 单次测量评定实例
如图1所示的某工件轮廓,需要评定的几何量包括凹槽跨长L,圆弧半径R,两个夹角。特征辨识的主要依据如下:
(1)直线转接直线:转接处角度变化率出现一个明显的非零值,或者连续多个明显的正值或负值;
(2)直线转接圆弧:圆弧处角度变化率出现连续三个或者三个以上明显的正值或负值;
(3)水平直线段:角度变化率接近0,只需设定合理的阈值将其区分出来。
图4、图5分别为直线转接直线和直线转接圆弧处的采样拟合。图6为计算评定过程中的斜率和角度变化率,角度变化率为方便观察经过比例缩放,特征评定时采用原始数据。特征评定过程中,直线转接直线处,斜率与角度变化率较小,通过特征滤波算法避免了由此带来的影响。如图7所示,该算法有效识别出了直线与直线,直线与圆弧的转接处,实现了几何特征点的抓取。
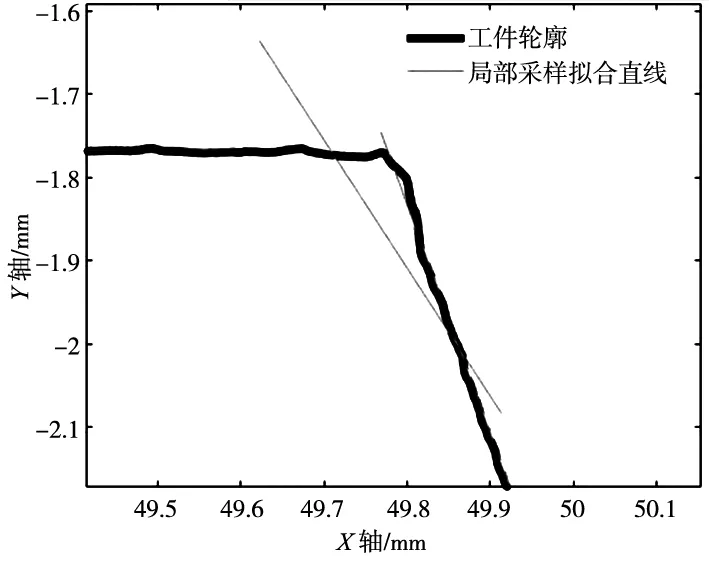
图4 直线转接直线处采样拟合
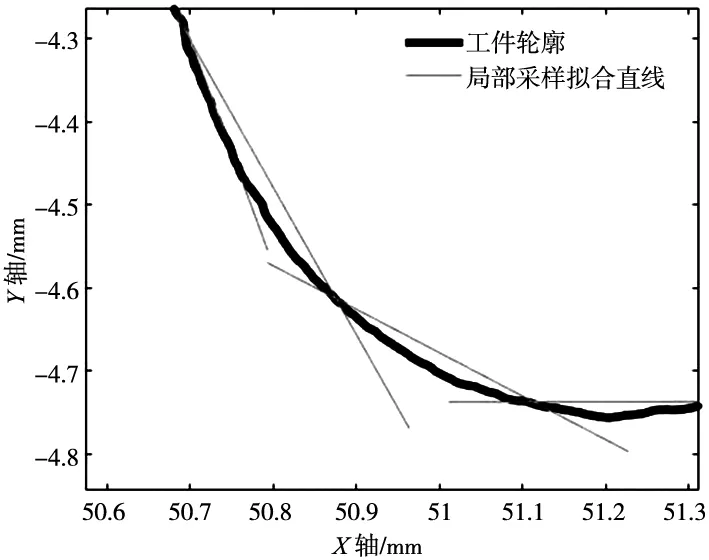
图5 直线转接圆弧处采样拟合
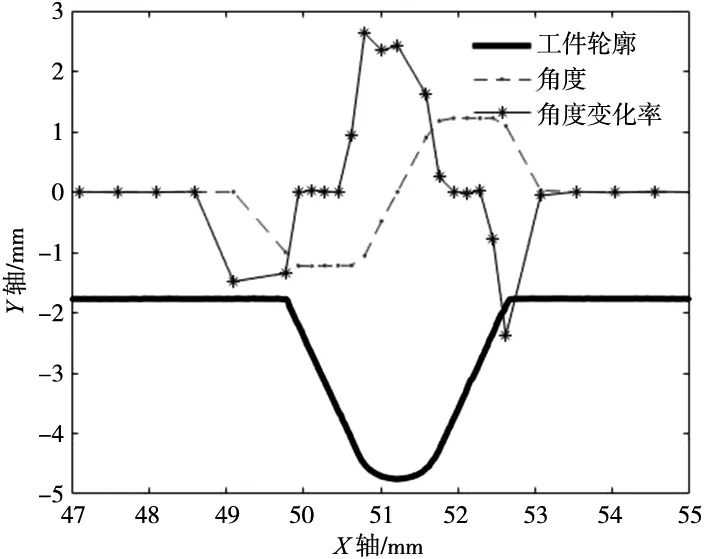
图6 斜率和角度变化率图
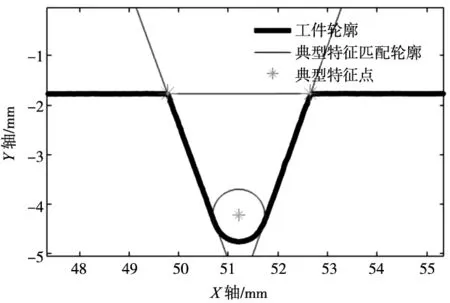
图7 几何特征点匹配图
为了校验特征辨识、滤波和评定算法对工件不同放置角度时测量评定的鲁棒性,对工件倾斜放置时再次进行了测量评定,图8为几何特征点的匹配结果,表1为几何尺寸评定结果。可以看出,水平放置与倾斜放置时几何尺寸评定结果长度误差小于10 μm,角度误差小于0.02°,说明该算法的鲁棒性较强。
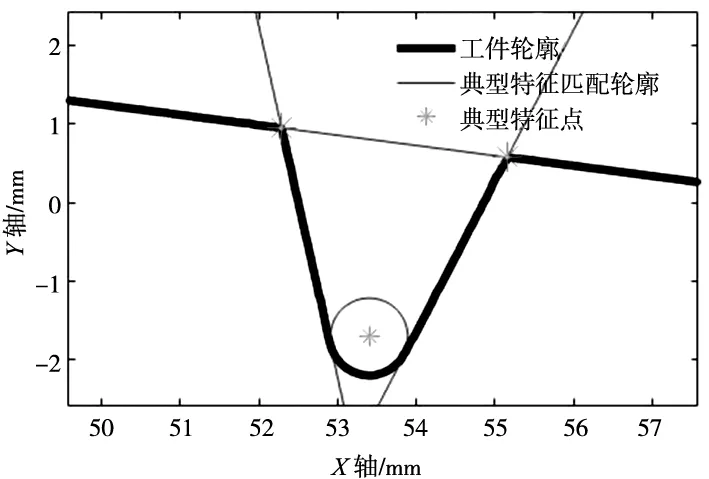
图8 工件倾斜放置时几何特征点匹配图
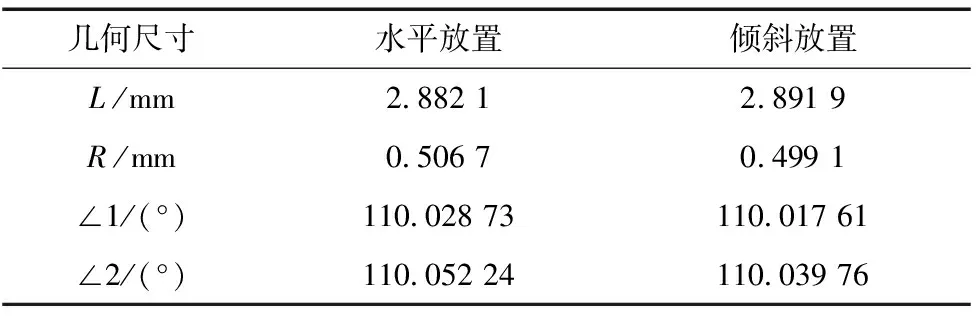
表1 工件水平与倾斜放置测量评定结果
2.2 多次测量评定实例
为进一步验证本文算法多次测量评定的效果,对图9所示的工件轮廓随机倾斜角度放置9次,进行主要尺寸数据的测量评定。多次测量时,每次工件测量的绝对坐标值都会发生变化,误差的分布率也会变化;为提升评定精度,评定时取相对坐标值,相对坐标误差分布率也都相同。图10是第一次放置位置时圆弧段几何特征点匹配图,找出了拟合圆弧的圆心。
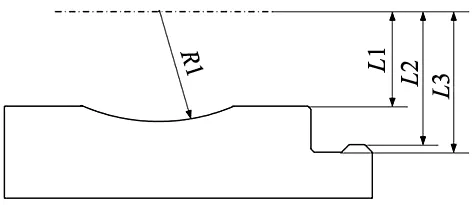
图9 工件2轮廓示意图
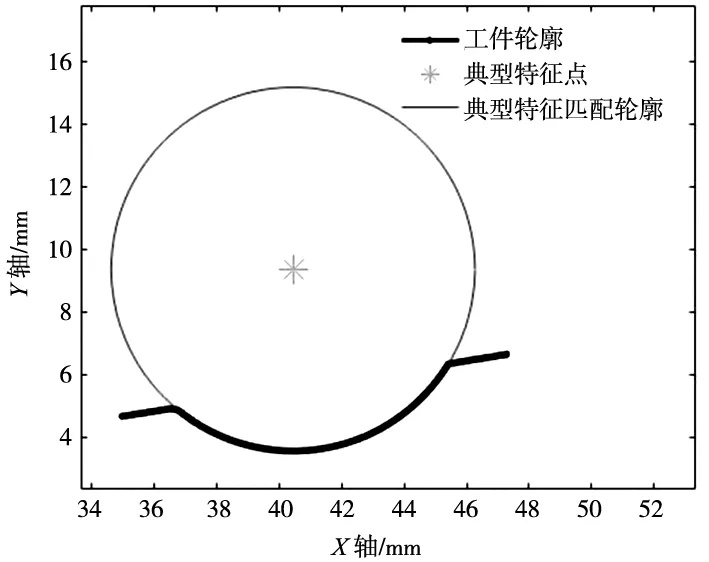
图10 圆弧段几何特征点匹配图
9次测量评定出的圆弧半径如表2所示。该圆弧的实际值为5.80 mm,9次评定的半径平均值为5.811 2 mm,在机测量评定误差小于13 μm。当测量次数达到20次时,测量评定的半径均值为5.800 0 mm。可见单次测量的精度较高,多次测量消除的只是随机误差。
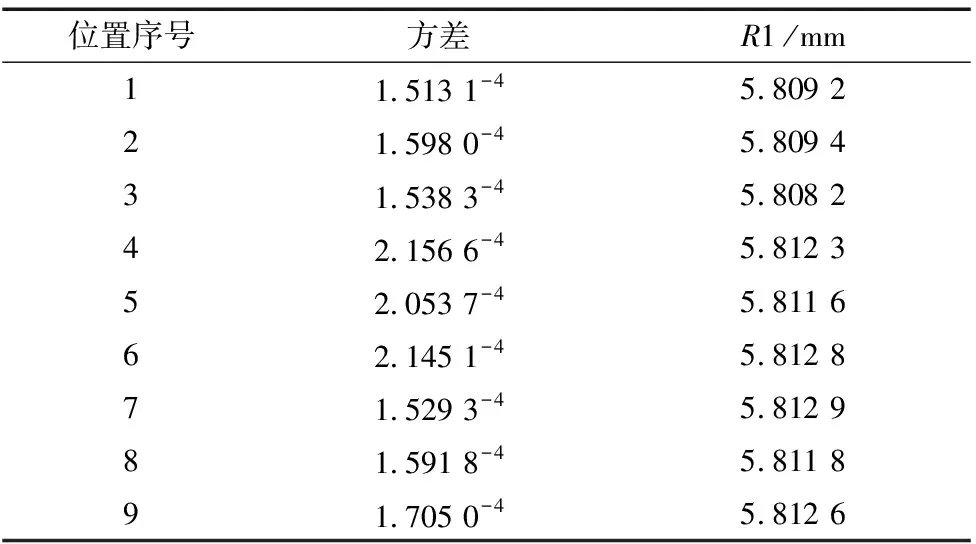
表2 同一圆弧不同位置放置评定结果表
对图9所示工件中的直线段,第二次放置位置时的几何特征点匹配结果如图11所示。表3为直线段9次不同位置放置时的评定结果。L1的平均值为3.766 1 mm,L2的平均值为5.951 0 mm,L3的平均值为6.341 9 mm。3个尺寸的实际值分别为L1=3.77 mm,L2=5.95 mm,L3=6.34 mm,在机测量评定误差小于5 μm。
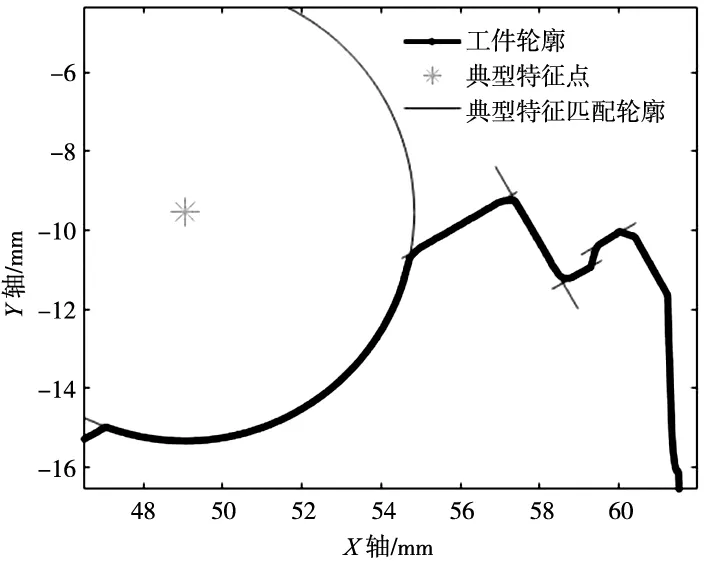
图11 直线段几何特征点匹配图
3 结论
复杂工件轮廓在机测量中,由于单个几何特征数据量小,转接处易受到噪声干扰,单纯使用最小二乘法拟合评定具有一定的局限性。本文提出了特征辨识和滤波算法,将工件复杂轮廓数据分解成水平直线段、倾斜直线段和圆弧段等典型几何特征,开发了相应的特征评定算法,并进行了实例分析,结果表明:
(1)在工件随机放置的状态下,特征辨识和滤波算法能有效识别出特征转接处信息,准确提取出几何特征点,实现了典型几何特征的分解。
(2) 单次测量评定的长度误差小于10 μm,角度误差小于0.02°;多次测量评定的长度误差小于5 μm,半径误差小于13 μm,该算法能满足智能制造在机测量的需求。

