基于改进贪心算法的Delta机器人分拣路径优化
赵铁军,王 玲
(沈阳工业大学机械工程学院,沈阳 110870 )
0 引言
在工业分拣和包装领域中,为了降低生产成本提高生产力,并联机器人发挥了重要作用,尤其Delta并联机器人[1]成为了应用最为成功的并联机构之一[2]。结合机器视觉的分拣系统比传统的分拣生产线更能适应多变的作业环境,显著地提高生产效率。基于此,研究者主要针对动态目标点到固定放置点的单传送带分拣场景分析[3-5],优化抓取顺序,以提高分拣效率,但这种分拣场景已经不能满足于当下以至未来工业分拣领域的需求[6],为了优化上述分拣场景,把放置点设置为动态,即包含双传送带的分拣系统。但当前分拣路径的策略普遍采用并联机器人以优先抓取传送带方向最前端物料的策略实现双传送带分拣系统的动态抓放,未能充分发挥自动化生产的优势,文献[3-5]中所采用的遗传算法和粒子群算法只针对优化放置点固定的场景,不满足双传送带系统实时性要求。针对以上问题,对于双传送带分拣场景,提出一种基于改进贪心算法的高速分拣系统,确保每个 “门”形分拣轨迹进行最优化处理的同时,对处于每一个节拍中的所有物料进行基于改进贪心算法的动态目标最短分拣路径的整体排序规划,由此提高分拣系统的生产效率。搭建分拣系统进行分析,以期为未来基于并联机器人的高速分拣产业提供参考依据。
1 分拣系统介绍
基于视觉Delta并联机器人分拣生产线结构如图1所示,随机分布的物料随传送带匀速进入视觉采集区域,工业相机把固定频率采集传送带上物料的位置信息传送给上位机系统,上位机系统根据传送带的速度、物料的位置信息、相机触发时间信息、机器人的运作方式对这一节拍内物料的分拣路径进行规划优化。计算运动目标的抓取位置和放置位置,将位置信息规范化处理后传输为机器人系统, 最后通过伺服马达驱动各个关节,使末端执行器完成物料的高速分拣操作。
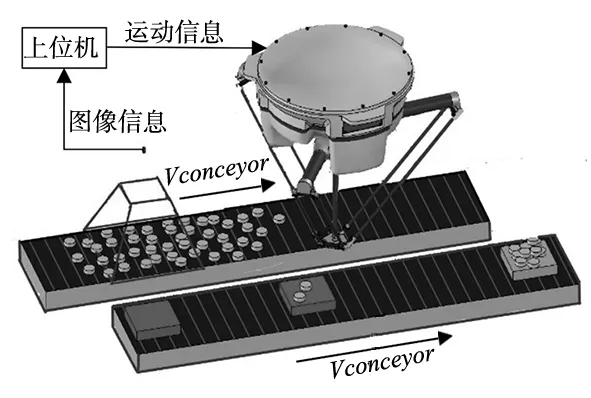
图1 抓取物体到运动点场景
平面模型如图2所示,建立原点为O的全局坐标系,X、Y方向如图所示,G为末端执行器的起始点,虚线圆区域是Delta机器人的工作空间,x1到x2是系统分拣区域,图的左边以v1的速度从上到下传输物料,右边以v2的速度从上到下传输托盘,E为托盘放置点,把装满托盘任务作为一节拍,机器人在分拣区域内完成一次节拍任务后,上料机构会在E点重新放置空托盘。
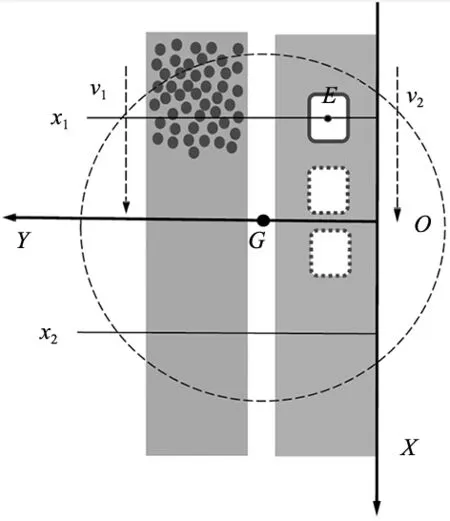
图2 场景平面模型图
2 轨迹规划
2.1 直角坐标空间轨迹设计
轨迹规划的目的是使机器人末端执行器的运动时间和机械性能最优,延长使用寿命。在分拣场景中,Delta机器人主要用于点到点的操作,分拣过程中也必须要避开箱子的高度或一定宽度的障碍物,所以这里采用近似“门”型的路径规划轨迹,如图3所示。
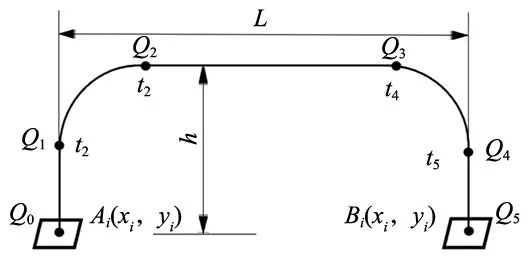
图3 “门”型的运动轨迹
2.2 修正梯形加速度轨迹规划
常用的轨迹算法有正弦加速度曲线,多项式加速度曲线和梯形加速度曲线[7-8]。这里选用梯形加速度曲线,它具有加速度快,速度过渡较为平滑等优点,但在高速运动下阶跃度和跳度不连续,为更好地减轻震动和冲击对机器人本体带来的影响得到更加平稳的运动,以正余弦函数为过渡阶段对梯形加速度曲线的加减过渡段进行修型。
(1)
(2)
通过以上分析,当t=T时,求得周期T的表达式为:
(3)
2.3 路径拟合
“门”型运动轨迹采用三段直线运动路径合成方法[9],图3所示每段直线运动都进行正弦修正梯形加速度曲线规划。轨迹的具体实现过程为:0时刻机器人抓起物体竖直向上运动,t1时刻运动到Q1后,启动水平运动(结合实际要求和易于编程这里Q1=h/2),此时为竖直运动与水平运动合成的平滑过渡曲线,运行到t2时刻变为水平运动,t3时刻启动竖直向下运动,这时为竖直向下运动与水平运动合成的平滑过渡曲线,t4时刻到T时刻完成竖直运动,整个运行周期为T。
T=2×t1+T′
(4)
其中,T′为运行水平距离L所用的时间。
3 分拣路径优化
3.1 传统分拣策略
将一次分拣任务作为一个节拍,则分拣任务由无数次节拍组成,如图4所示,箱子的容量为常数n,每个拾取放置“门”型轨迹高度为h。传统分拣系统以保持物料最小x坐标值的优先级策略,为了表达式更易描述,这里总行程S表达的是直角过渡的“门”型轨迹(2.3小节中合成的曲线轨迹将在表达式(12)中具体描述)。
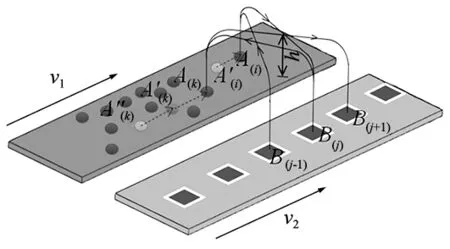
图4 传统分拣系统简图
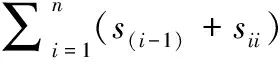
(5)
(6)
(7)
其中,s(i-1)i是放置点B(i-1)到拾取点Ai的距离,Sii是拾取点Ai到放置点Bi位置的距离。物料放置点在传送带上的位置实时变化,因此放置点B拾取点A总行程S都是自变量t的函数,上述公式可以改写成下列式子:
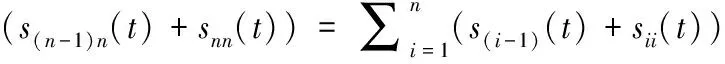
(8)
(9)
(10)
3.2 贪心算法
贪心算法的基本思想是只选取当前看来最好的局部解,而不去考虑对以后步骤的影响,它的时间复杂度比较低,算法实现比较容易[10]。基于此,对于双传送带高速分拣场景,该算法满足分拣系统实时规划抓取顺序的要求。
3.3 贪心算法分拣策略
基于贪心算法分拣系统总体的思想为遍历工作空间内传送带上所有物料与动态放置点的距离,找出离放置点B位置最近的物料Ai,如图5所示。
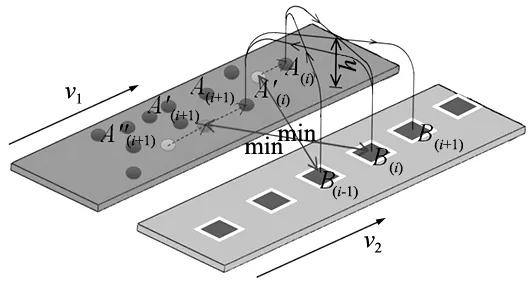
图5 基于贪心算法分拣系统简图
传统的排序方式:
O→A1→B1→A1→B2→A3→
B3→…→Ai→Bi→…→An→Bn
贪心算法的排序方式:
O→Ai→B1→Aj→B2→Ak→
B3→…→Am→Bi→…→An→Bn
通过下列式子找到离B位置最近的物料Ai。
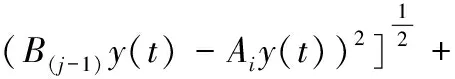
(11)
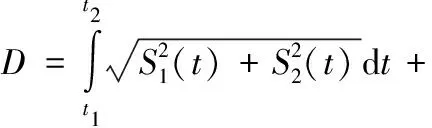
(12)
其中,S(j-1)i(t)是放置点B(i-1)到拾取点Ai的距离,sij(t)是拾取点Ai到放置点Bj的距离,S1,S2分别为t1到t2时刻竖直和水平方向上的运动位移,S3,S4为t3到t4时刻水平和竖直方向上的运动位移,D为执行器末端在竖直和水平方向同时运动拟合圆弧过渡段所走的实际轨迹位移。然后由下列公式推出x方向上动态放置参考点Bjx和动态抓取参考点Aix坐标值。
(13)
Bjx=B(j-1)x+(T(j-1)i+Tij)v2
(14)
其中,v1为拾取传送带的速度,v2为放置传送带的速度,T(j-1)i为执行器末端抓取过程用的时间,Tij为末端执行器放置过程用的时间。
3.4 改进贪心算法分拣策略
本文描述的最优路径是指放置点与物料最近的距离,而不是传统算法中放置点与物料所对应的x轴上最小坐标值的距离。采用贪心算法的分拣策略后会存在丢失材料的风险,如图6所示与工作空间内的下限越近,遗漏的风险越高,因此将系统中加入最小下限值xmin以及在贪心算法中融入评估函数f来避免这种风险。
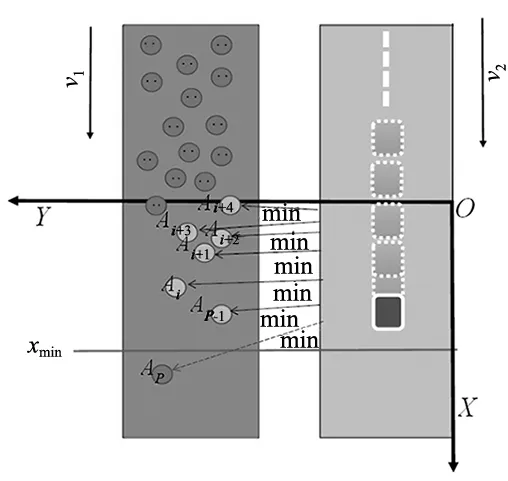
图6 遗漏物料风险图
此时目标函数S(t)表达式为:
S(t)=s(j-1)i(t)+sij(t)-γ×f(Aix(t))
(15)
(16)
其中,Aix是第i个物料在传送带x轴上的坐标值。
利用表达式(15)对物料位置进行综合评估,通过改进贪心算法的评估标准,提高了生产效率,同时还做到尽可能不遗漏任何物料。最终整合成本函数L(t)后,得出评估优先顺序为:
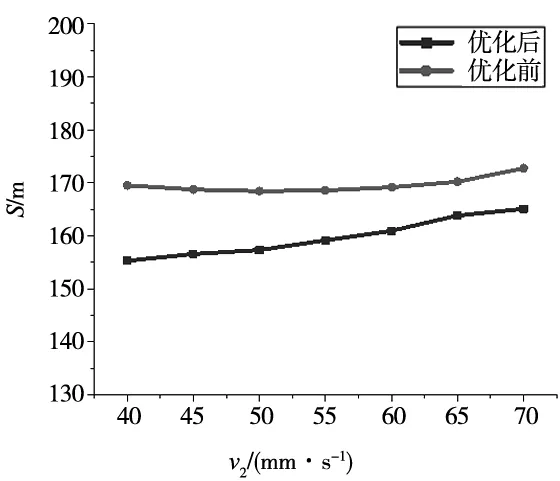
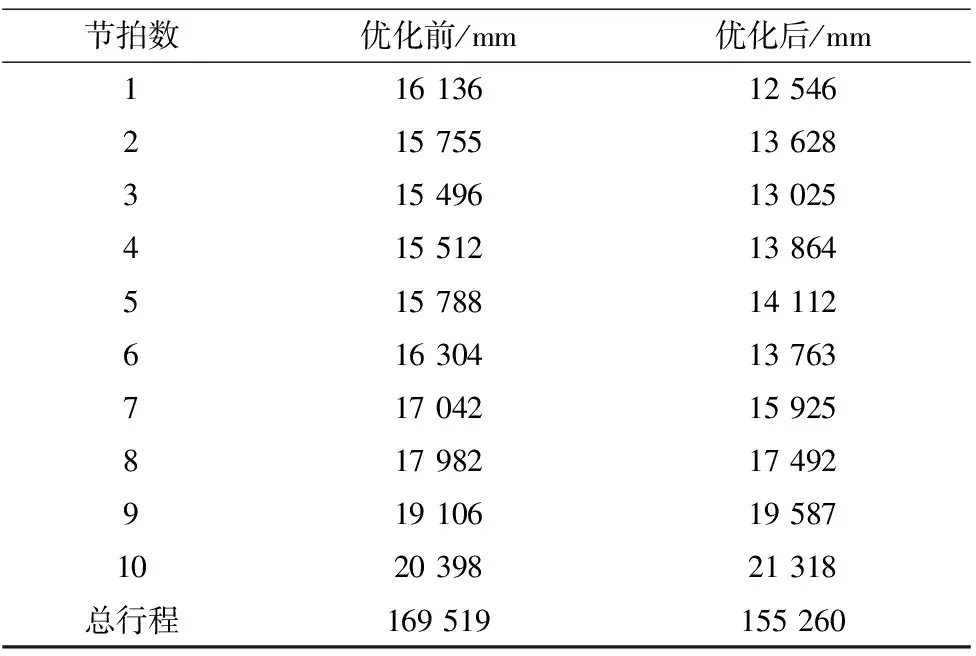
LAp(t) (17) LAp(t)=(sB(j-1)Ap(t)+sAmBj(t))-γf(Apx(t)) (18) LAq(t)=(sB(j-1)Aq(t)+sAqBj(t))-γf(Aqx(t)) (19) (p≠q) 搭建两种分拣策略模型,第一种为传统的分拣策略,根据物料的x坐标值从大到小的固定排列顺序,放置点与物料运动方向相同的匀速运动,第二种为改进贪心算法分拣策略,放置点与策略一相同。 完成每个从Ai到Bj单个拍子的过程中,系统就会实时规划下一个Ap到Bj+1的分拣轨迹,当机器人把物料从Ap分拣到Bj+1过程中,系统将继续规划下一个物料Aq到Bj+2的轨迹,以此类推下去。如图2平面模型所述,假设机器人的工作空间直径为1200 mm,传送带宽500 mm,末端最大加速度为35 m/s2,xmin=200 mm,G点为(550,0),E点横坐标为25,为了生产中安全性和运动控制系统的可行性,把x1为-500 mm,x2为500 mm作为分拣区域的上下限,传送带上每0.5 m随机分布120个物料,假设以装满箱子物料数12个为一个节拍,10个节拍为一次分拣任务测试上述的两种策略。 为确保两种策略性能对比的可行性,即Delta机器人抓取不超过工作空间的上下限,把v2的运动速度设置为55 mm/s,实验结果如图7所示。 图7 两种策略的结果对比图 S为完成一次分拣任务时末端所走的水平方向行程的总和。由图7可知,随着v1速度的提高,优化效果更加的明显,当v1的速度为8 mm/s时,传统策略中物料会超出机器人的工作空间,不能完成分拣任务。这里列出v1=7.5 mm/s时,一次分拣任务每拍路径数据对比,如表1所示。 表1 传送带速度v1为7.5 mm/s时结果 续表 上述数据可以得出传送带速度v1为7.5 mm/s时分拣120个物料,优化后比优化前的总行程缩短10 m距离,证明了改进的贪心实时规划算法在动态抓取与动态放置的分拣场景中的效率高于传统以坐标值为优先级的分拣策略。但表1中8和9节拍中,没有优化前的效果好,这是与xmin的取值有关,由于已经验证了改进的贪心规划算法在文中所描述的分拣场景中完成一次分拣任务的高效性,这里将不再讨论xmin取值对分拣系统效率的影响。 在双传送带高速分拣系统中,传送带v2的速度也是影响整个分拣系统效率的关键因素。由图7可知,当v1=7.5 mm/s时分拣效率最高,但为确保分拣系统的可行性和安全性,这里选用v1=7 mm/s对优化前后的分拣系统进行实验,结果如图8所示。 图8 两种策略的仿真对比图 再次验证了改进贪心算法分拣策略优于传统的分拣策略。下面列出分拣效果最佳的v2=40 mm/s时优化前后的数据结果,如表2所示。 表2 传送带速度v2为40 mm/s时结果 v2为40 mm/s,v1为7 mm/s时,在文中所描述的场景模型中完成120个物料分拣任务,改进的贪心算法分拣系统比传统以物料x坐标值为优先级的分拣系统总行程缩短了大约15 m,效率提高了8%。 本文介绍了包含双传送带的高速分拣系统,并用Delta机器人在高速分拣系统中对物料进行分拣操作,用改进的贪心算法对分拣顺序进行实时的规划,也同时考虑了丢失材料的风险。实验表明,不同的v1和v2,改进贪心算法分拣系统比传统分拣系统的效率高,当v2为40 mm/s,v1为7 mm/s时该分拣策略比传统以物料x坐标值为优先级分拣策略执行相同任务时系统的分拣效率提高了8%。同时也验证了该分拣算法满足双传送带分拣系统的实时性要求,具有高稳定性,计算简单,易于编程的优点。4 实验验证
4.1 模型的搭建
4.2 结果分析



5 结论

