基于kriging模型的大功率液力变速器支撑优化*

谢国平，杨旭东，孙 栋，周志祥，陈 波

(贵州大学机械工程学院，贵阳 550025)

0 引言

传统的有限元法分析在涉及多学科、多目标的复杂优化问题上计算慢，效率低，而代理模型有计算量小，不降精度等优点，提高分析效率且能满足一定的设计要求。王强等[1]使用kriging近似模型替代物理模型对副车架进行轻量化设计，优化后副车架质量较优化前减轻10.3%，且固有频率满足模态要求。近似模型是利用数学函数表达式对输入变量进行设定，来调整目标函数的值，从而获得未知点响应值。在建立kriging代理模型的过程中，需要在设计变量的可行域内抽取样本用于构造kriging函数，样本抽取的好坏直接影响kriging函数对有限元模型模拟的精度[2]。本文采用的抽样方式为拉丁超立方抽样，该抽样可以保证kriging函数的精度,正如文献[3]中，采用拉丁超立方抽样对滑动适配器相关变量进行抽样，最终通过优化后，质量减轻12.73%，改善度为52.39%。

大功率液力变速器试验台是大功率液力变速器出厂前的一种试验检测装置，试件支撑作为试验台的关键结构，对试验整体性能影响重大[4]。针对某型液力变速器试验时，当档位增至7挡，转速为1600r时，由于试验台支撑振动过大，引起系统报警而试验中止。经检查，变速箱连接法兰壳体处开裂。随即更换同型号另一台变速箱测试，在相同位置再次开裂。经分析，由于支撑结构在重载高压下，发生了位移偏动，导致台架对中系统受到影响。本文针对试件支撑结构固有振动性能差，对支撑结构采用有限元分析与参数分析相结合的方法进行结构优化。

1 kriging模型建立

1.1 拉丁超立方抽样

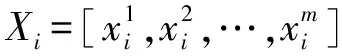
(1)

针对样本粒子群种群规模较大的问题，提出了一种插值抽样方法。在拉丁超立方抽样的基础上，利用控制变量法分析其他变量对目标函数值的影响，得到各变量对目标函数的Pareto解集，对权重和比例系数大的区域进行插值，使得目标函数的最优值更接近真实值。具体插值抽样流程如下：

(1)拉丁超立方抽样抽取m个样本点；

(2)计算目标函数的所有自变量权重，得到目标函数的Pareto解集；

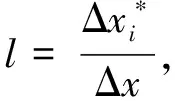
(4)对最优解区间[xNmin,xNmax]进行插值抽样，得到新的样本点。

1.2 kriging模型构建

kriging模型作为参数优化的常有方法，被广泛应用于工程问题具有高度非线性等问题上，受到国内广大学者们的广泛应用[7]。它的工作原理主要是对设计变量分析，拟合出自变量与因变量之间的函数，然后通过已知点对未知点的输出变量进行预测。kriging模型是一种多维插值技术，同时考虑多方面影响因素，所以求得的函数值具有实际意义。kriging模型对未知点的预测，可由已知点的真实值表示为[8]:

G(x)=fT(x)β+Z(x)

(2)

其中，f(x)=[f(x1),f(x2),…,f(xm)]T表示均值基函数，其值为常数，大小对模型精确度没有影响，β表示f(x)的均值系数。Z(x)表示误差函数，具有以下特征：

(3)

其中，R(xi,xj,θ)表示第i个样本点与第j个样本点间的关联函数，θ为相关参数，R(xi,xj,θ)可由Gauss方法解得。

2 支撑结构优化

2.1 支撑结构工作原理

图1 支撑结构实物图

变速器在进行出厂试验时，被试件输入端与变速器支撑通过螺栓连接，输出端与加载轴连接，如图1所示。变速器支撑为变速器出厂试验提供了支撑与对中作用，在试验过程中起重要作用。

支撑结构机械性能直接影响了整个台架的工作可靠度，甚至直接损坏被试件。在一次试验过程中，因支撑结构振动稳定性较差的原因，导致被试件壳体发生断裂，断裂情况如图2所示。

2.2 支撑结构有限元分析

图2 变速器壳体裂纹

在建立kriging模型前，需对支撑结构进行有限元分析。在Solidworks中建立支撑结构三维模型，在进行有限元分析前，对三维模型进行适当的简化，将简化后的模型导入Abaqus软件中进行模态分析，得到了支撑结构的前30阶固有频率和振型。支撑材料属性如表1所示。

表1 支撑结构材料属性

模型有限元分析具体步骤如下：

(1)根据表1定义支撑的材料属性;

(2)支撑通过地脚螺栓与铁T型槽连接，因此螺栓孔采用固定约束，支撑底板施加z方向移动约束;

(3)对支撑模型进行网格划分，共生成了17 182个C3D10四面体单元，30 737个节点，提交分析作业，表2为支撑的前6阶固有频率，可发现固有频率随阶次的增加而增加，1阶固有频率为110.94 Hz，也是前6阶固有频率最小值，如发生失效，激振力最有可能先与1阶固有频率发生共振。试件试验时，最高转速为6000 r/min，最大激振力频率为100 Hz，激振力频率与模型1阶固有频率比较接近，直接威胁试验台工作性能。有必要对模型结构进行分析与优化，主要研究模型1阶固有频率的取值与各变量之间的关系。

表2 模型前6阶固有频率

2.3 模型支撑块模态分析

实验过程中，支撑大圆端面主要与试件连接，支撑着时间正常进行试验，观察支撑结构，支撑边沿焊接了5块支撑块结构。分析不同数量支撑块对模型固有频率的影响，将三维模型导入有限元分析软件Abaqus中进行分析，研究不同数量支撑块对模型模态影响，主要分析了支撑块数为0、2、3、4、5对模型一阶固有频率的影响。表3为不同支撑块与对应的目标值，不难看出通过适当减少支撑块数量，模型固有频率有所提升。2个支撑块时，模型一阶固有频率为147.02 Hz，其次是0个支撑块时，模型一阶固有频率为140.72 Hz，本着轻量化设计原理，在模型固有频率提升的同时，降低模型质量是实现节能环保的重要途径，由于0支撑块与2支撑块的目标值差距不大，接下来主要对0支撑块模型的其他结构进行分析[9]。

表3 不同支撑块对应1阶固有频率

(a) 模型支撑块结构优化前 (b) 模型支撑块结构优化后图3 5支撑块与0支撑块模型固有频率

2.4 模型约束数量模态分析

模型与T型平板通过螺栓连接，将模型固定在平板上，在固定模型底板4个角的基础上，研究不同数量螺栓孔对模型固有频率影响。主要研究约束为4、6、8、10四种约束情况下，目标函数值的变化规律。表4可看出模型目标函数值受约束数量影响不大，8约束时略高于其他约束的目标函数值，因此本文以8螺栓孔为设计基础，并在此基础上研究其他结构的目标响应值。

表4 不同约束对应模型一阶固有频率

2.5 变量设计

在进行参数分析前，需要对模型进行变量设计。变量设计主要选择模型中有变化余量且不影响结构根本使用的前提下进行选取，本研究主要对如图4中的3个支撑变量作为参数分析的变量，其中x1表示前加载轴孔半径，x2表示大端面内半径，x3表示中间过渡段。首先对3个设计变量进行拉丁超立方抽样，对抽取的参数建立相应模型并导入Abaqus分析，分析出相应的目标函数值，将自变量与相应的因变量组成一个样本点，将各样本点数据导入MATLAB中进行kriging拟合求解。

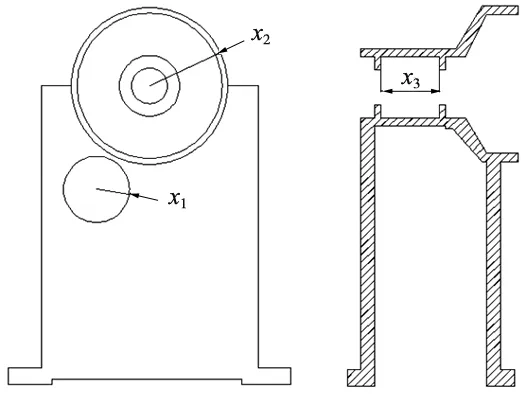
图4 支撑设计变量

表5 变量取值范围

2.6 样本点对应响应值

应用拉丁超立方抽样对3个变量进行抽样，本次设计了40个样本点。根据样本点参数，建立对应的三维模型，并将模型导入Abaqus中进行分析，分析结果如图5所示，横坐标表示样本点数，纵坐标表示样变量值，一个样本点上对应有4个值，分别为x1，x2，x3和f(x)的值，也代表一个样本点的坐标值。其中线性f(x)表示目标函数f(x)的趋势线，不难看出目标函数值始终在110～120附近波动。

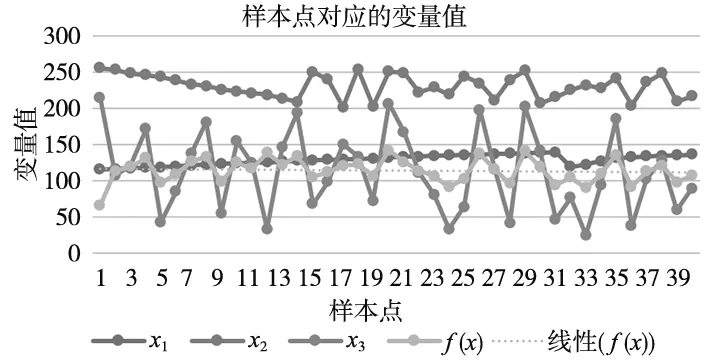
图5 样本点对应的坐标值

3 PSO优化算法

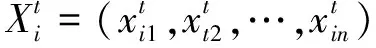
(4)

(5)

(6)

其中，w为惯性权值，c1与c2为加速因子，r1与r2为随机数，pij表示当前粒子最优，gj表示全局最优。通过位置与速度不断更新，从而获得粒子全局最优。

4 设计优化结果及验证

通过PSO优化算法对参数模型进行优化，在约束范围内目标函数值提升到146.17 Hz，质量降低了57.411 kg。表6为kriging模型优化前后参数比对，优化后可看出x1、x2增加，x3有显著减小。同比目标函数值显著提升，得到减轻。

表6 kriging模型优化前后模型对比

图6为kriging模型优化后的模型振型图，根据kriging模型参数建立三维模型，导入Abaqus中求得模型目标值。对比支撑模型kriging模型优化目标值与有限元分析目标函数值，分析了目标值误差在0.31%左右。接着对kriging模型进行随机抽样，并建立三维模型有限元分析，结果分析显示误差在0.8%左右，验证了kriging精确性[7]。

图6 kriging模型优化

对优化后的模型进行试验验证，安装优化后的试件支撑，并调整对中。图7表示支撑结构在进行结构优化前后的对中情况，可看出支撑结构优化前的对中性较差，经检测支撑结构在x轴位移偏动量为5 mm。

(a) 优化前对中 (b) 优化后对中图7 支撑优化前、后对中效果

装机试验，在同一机型7挡相同速度下，支撑结构振动速度有效值如图8所示，优化前振动速度有效值为6.97 mm/s，优化后振动速度有效值为5.69 mm/s，同比减少了1.28 mm/s，且优化后的振动速度有效值稳定在振动安全范围内，不会引起系统报警，试验验证了优化后得支撑结构振动稳定性得到提高。

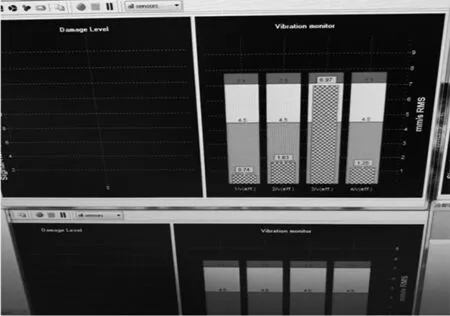
(a) 支撑优化前振动速度有效值

(b) 支撑优化后振动速度有效值图8支撑优化前、后振动速度对比

5 总结

(1)在Abaqus中对模型进行结构分析，研究不同支撑块数与约束数量对模型固有频率的影响，得到了模型固有频率有所提高的0支撑块8约束模型结构，该结构为模型的振动稳定性提供了理论基础。

(2)选取3个变量作为参数优化变量，利用拉丁超立方插值抽样抽取40个样本点，并应用kriging模型对支撑结构建立参数建模，然后通过PSO对模型进行优化求解。优化后模型目标函数较优化前提升了31.97%，远高于试件产生的激振力频率，同时模型质量减轻了51.414 kg。对PSO优化后的参数进行三维建模和有限元分析，分析结果误差为0.31%，验证了kriging模型的精度与准确性。

(3)通过试验验证，优化后支撑结构的振动速度有效值降低至5.69 mm/s，支撑结构的稳定性得到显著提高。