基于静压轴承的非圆轨迹成型及控制*

詹 烁，潘 伟，张艺馨，黄 冉，路长厚

(山东大学 a.机械工程学院；b.高效洁净机械制造教育部重点实验室；c.国家级机械工程实验教学示范中心，济南 250061)

0 引言

非圆内孔以其均匀载荷，减小应力集中，提升零件的寿命等优点在机械设备中得到了广泛的应用。这些非圆内孔形状复杂，精度要求较高，普通的加工方法难以满足应用需要，因此对制造加工技术提出了更高的要求。随着技术的发展，针对非圆内孔加工的方法已经相继出现，但是低成本的非圆内孔加工技术仍然在探索中[1]。

在当前工业生产中，机械零件的内孔加工通常由镗床或钻床来完成，其中安装刀具的主轴旋转为主运动，通过刀具或零件的进给运动完成内孔的加工。由此可得，对于机械零件非圆内孔的加工，当使机床主轴的运动为非圆轨迹时，即可实现非圆内孔加工。因此，一种可行的非圆内孔加工方法为通过控制主轴的轴心轨迹来实现期望的非圆内孔加工[2-3]。其中对于主轴运动轨迹的承载元件，可以选取不同种类的轴承(气体轴承，液体轴承和电磁轴承)来实现[4-7]。

实际上，相关研究已经在气体轴承、液体轴承和电磁轴承中展开。相对于气体轴承和电磁轴承，液体轴承在承载力和稳定性方面有着较大的优势，因此液体轴承对于实现主轴的非圆轨迹是一种较好的选择。文献[8-10]通过理论仿真对静压液体轴承的动静态特性进行了相关的研究，在理论上对液体轴承系统非圆轨迹的运动进行了推导验证。本文则是基于文献[8-10]中的工作来对系统非圆轨迹的反馈控制进行研究。在本文中，首先介绍了主控型静压轴承系统的机械模块和控制模块，并说明了系统的运行原理。然后完成了系统的建模及参数辨识工作，并对非圆轨迹进行了实验验证。最后在MATLAB中对系统在外部扰动下的轨迹响应进行了分析和仿真计算，并采用PID控制器对扰动下的系统误差进行了调节。

1 主控型静压轴承系统的结构与原理

1.1 主控型静压轴承系统的机械模块

本文所研究的系统结构如图1左所示，主要由静压轴承和4个节流器组成，其中连接上、左油腔的为压电薄膜节流器，连接下、右油腔的是小孔节流器，在上述节流器的共同作用下可实现主轴位置的主动调节；图1右为压电薄膜节流器的结构示意图，该装置采用压电陶瓷作为控制元件。在工作时，压电陶瓷通过顶杆推动薄膜改变其间隙，进而实现出油口流量的调节。因此，系统的轴心轨迹主动控制原理是通过压电薄膜节流器，对主轴的平衡位置进行调幅和调相，进而实现期望的平衡点运动轨迹；具体采用的方法是通过压电陶瓷的伸长改变油口间隙，进而改变流入静压油腔内的流量，完成对主轴运动的控制。

1.静压轴承 2.主轴 3.压电薄膜节流器 4.小孔节流器 5.涡流传感器 6.控制模块 7.油箱 8.压电陶瓷 9.薄膜

1.2 主控型静压轴承系统的控制模块

本系统的控制模块主要为主控模块、信号采集模块、D/A转换模块等，如图2所示。

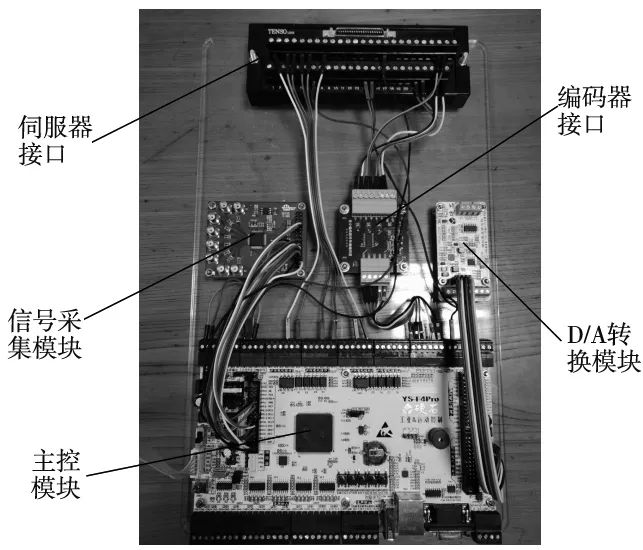
图2 控制模块

在本系统的主控模块中，其中控制芯片选取的是STM32F407，支持C语言开发，主控开发板中的扩展flash容量为16 M，共有6个串口，并拥有USB、编码器等接口。基于对本系统整体性能的考虑，需要采用其他功能模块对其进行扩展。对于D/A转换模块，其核心采用的是AD5689，该模块能够同时对外输出2路、电压范围为±10 V的模拟信号，信号经过外部驱动器即可对节流器中压电陶瓷输入电压范围为±100 V电压信号。信号采集模块的核心为AD7606，该模块支持同时8通道200 kHz的信号采集，并且能通过数字滤波器提供过采样功能。此外，用于电机控制的伺服器，采用的是松下交流伺服电机驱动器MINAS A4系列，其具有自动增益调整和自动调谐等功能。

本系统的运行方式是：在D/A模块输出信号时，数据采集模块同时开始采集主轴的运动信号，并储存在相应的设备中。主控模块基于采集的数据对输出数据进行计算，然后产生输出信号并通过D/A模块和驱动器输入节流器中，节流器根据输入信号对流量进行调节进而完成主轴运动的调节。

2 主控型静压轴承系统的建模与实验

2.1 实验设备

根据图1中的系统结构搭建实验平台如图3所示。设备相关的参数如表1所示。

图3 实验设备

表1 实验设备参数

在上述实验平台进行相关实验测试，在本实验测试中，系统的供油压力p=1.1 MPa，系统的采样时间为t0=0.2 ms。

2.2 系统模型的建立

对于本实验中的主控型静压轴承系统而言，通过雷诺方程等方法推导出的动力学模型难以用于控制且与实际情况存在显著差异，因此，需要简单的系统模型来进行控制工作。先前已经对本系统的建模进行过相关研究：由于本系统为非线性系统，可采用分段线性模型的方法对系统进行建模[11]，并通过系统辨识技术[12]获得模型参数的参数值。

对于系统动力学模型的建立，本文基于先前的研究方法，当输入信号幅值较小时，系统建立为线性状态方程模型，选取系统输入为压电陶瓷电压u=[ux,uy]T，输出为主轴的位移d=[dx,dy]T，将系统的噪声等效为误差项ξ，即：

(1)

此系统的系统矩阵，输入矩阵，误差矩阵，输出矩阵和状态向量为：

式中，K为等效刚度矩阵,C为等效阻尼矩阵,B为等效增益矩阵,E为误差矩阵,I为单位矩阵。

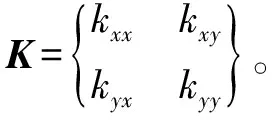
采用文献[11]的方法对系统模型中的未知参数进行辨识，获得的系统参数如表2所示。

表2 系统模型参数值

2.3 系统模型响应测试

在基于STM32的控制模块中，系统采用的是定时中断控制，即将主程序定时中断进入中断程序，在中断程序中进行信号产生、数据采集和闭环控制等功能。经过对试验台的所需功能的整体估算，本实验台控制模块的中断时间设定为0.2 ms，即每隔0.2 ms采集一次的数据和产生并输出一次信号。基于控制模块串口传输速度及储存芯片读写速度的综合考虑，实验中选择USB作为数据传输接口。此外，在设备初始化之后和设备停止工作之前分别设计手动开关，从而对该实验过程能实现更细致的控制并且保证实验的安全性。

为了得到合适的输入信号，需要对系统进行预实验。在系统的X和Y方向上分别输入电压幅值为-15 V～15 V，每秒增加1 V的阶梯信号，得到的系统响应如图4所示。

(a) X方向阶梯信号响应

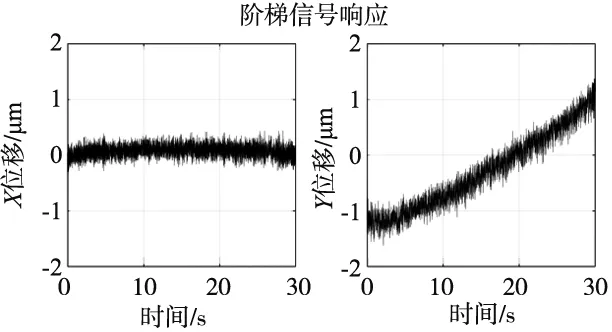
(b) Y方向阶梯信号响应图4 系统阶梯信号响应

可以看出，在-15 V～15 V的阶梯电压输入下，系统在X和Y方向的响应呈线性关系；同时系统的耦合响应位移较小，可以忽略。

基于上述实验结果，在本实验中，选取两路输入信号分别为幅值为15 V、频率为1 Hz的正弦和幅值为10 V、频率为1 Hz的余弦信号，实验结果如图5所示。由图5结果可得，在正余弦的输入信号下，系统响应位移的合成轨迹为椭圆，实现了系统椭圆轨迹的运动的目标。此外对2.2节中所辨识的模型在实验中进行的验证可知，辨识所得的模型能够较好地体现系统响应。

(a) 系统在X和Y方向上的响应位移

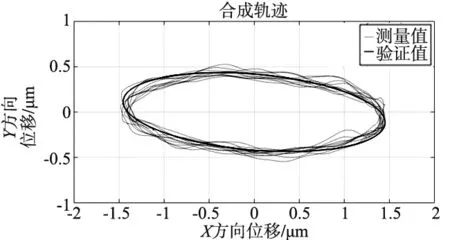
(b) 系统的响应位移合成轨迹图5 系统非圆轨迹测试

3 主控型静压轴承系统仿真

3.1 非圆运动误差分析

当使用镗床进行非圆孔加工时，如示意图6所示，首先使用钻床对工件加工出圆孔O，如图中的圆O所示，然后通过镗床对已加工的圆孔进行切削使其形成非圆内孔，需要镗床加工的部分为图中阴影部分。

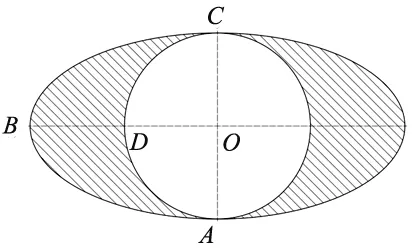
图6 非圆内孔形成示意图

当对非圆内孔进行加工时，由于在本系统中安装刀具的主轴在X和Y方向上并无其他的约束，故其受到不均匀的外力会导致安装刀具的主轴在X/Y方向产生位移波动。本文中选取刀具圆心和主轴轨迹圆心的连线与轨迹的长轴重合的地方来进行分析，如图7所示，当进行切削加工时，刀具在切削工件时对工件切削力的反作用力即为主轴受到外力。此时，主轴所受到的外力为：

(2)

式中，F为刀具的切削力，ω为刀具旋转角速度。

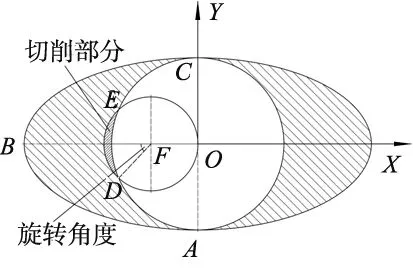
图7 非圆内孔切削加工示意图

但是，在实际的工件加工中，主轴受到的外力不仅仅为切削力，而是切削力和多种未知扰动的叠加，故主轴在工作时的合外力为可认为由多个不同频率的力叠加而成，即：

(n=1,2,3,…,k)

(3)

3.2 非圆运动误差仿真

对于本系统而言，其组成部分为静压轴承、主轴和节流器，主轴的非圆运动主要由节流器控制产生；直接作用于主轴的外部扰动力为系统误差。因此，系统中主轴的位移实际上为非圆运动与扰动响应的叠加。本文在MATLAB中对主轴在扰动影响下的轴心轨迹进行简单的仿真研究。

仿真模型基于2.2节中辨识的系统模型和2.3节中的系统输入下的非圆轨迹，对主轴受力后的轴心轨迹变化进行仿真计算。对于外部扰动响应，根据方程(3)可知，外部扰动可认为多个不同频率力的叠加。在仿真计算中，采用三个频率不同的信号，其表达式分别为：

(4)

(5)

(6)

将上述扰动响应与非圆轨迹叠加，仿真计算结果如图8所示。

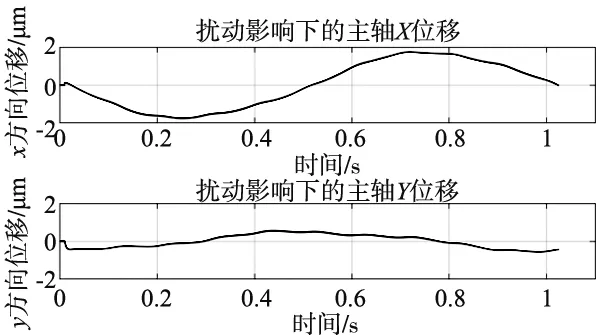
(a) 扰动影响下主轴在X/Y方向上的位移

(b) 扰动影响下主轴的轴心轨迹图8 扰动影响下的主轴仿真轴心轨迹

3.3 非圆运动误差调节

基于图4中的响应位移实验结果可得，在此区间的电压输入下，系统响应近似呈线性并且耦合性较弱，故对于式(1)，在该区间内可近似当作为X和Y方向的单输入单输出线性系统。

在上节的仿真计算可得，当主轴受到外部扰动后，其轨迹会产生较大的误差，对其加工精度产生影响。因此，对于上节外部扰动下的系统响应，本文采用PI控制器对其轨迹进行调节，如图9所示。

(a) 调节后主轴在X/Y方向的位移

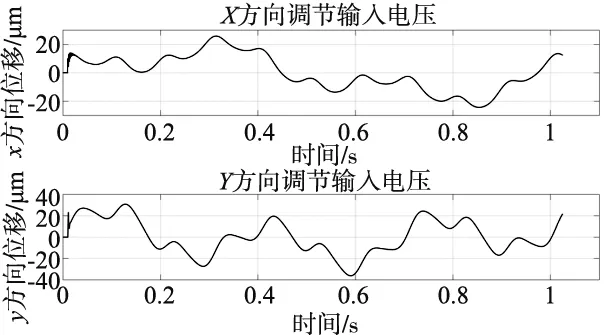
(b) 调节时系统在X/Y方向的输入电压

(c) 调节后主轴的轴心轨迹图9 调节后的主轴仿真轴心轨迹

由图8b中的轨迹可知，外部扰动对系统的运动精度有着较大的影响。在扰动影响下，主轴的运动轨迹与理论轨迹最大偏移量为0.125 μm，平均偏移量为0.085 3 μm。由图9c的结果可知，在PI控制器对于主轴的运动进行了调节后，其运动轨迹与理论轨迹的最大偏移量为0.021 2 μm，平均偏移量为0.011 3 μm。与图8b中未调节的曲线相比，其最大偏移值减少了83%，平均偏移值减少了86.7%。由此可知，PI控制器有效地减小了运动误差，保持了系统的非圆运动精度。

4 结论

(1)针对当前非圆内孔较难进行精密加工的问题，结合镗床等设备的工作特点，本文采用静压轴承-主轴-压电式节流器组成了轴心轨迹的主动控制系统，阐述了系统的整体机械结构和测控电路，并通过实验实现了非圆运动轨迹。

(2)采用分段线性化方法，通过参数辨识建立了系统的整体模型；对于非圆曲面加工时外部的切削力进行了分析，进而得到了外力的扰动方程，并将其近似为几个主要的频率成分的叠加。在此基础上，对于系统在外力作用下的运动轨迹，进行了仿真与分析。

(3)为补偿系统的外部扰动，设计了PI控制器，实现了系统误差的补偿，仿真实验证实系统非圆轨迹的精度有了显著的提高。此外由于实验设备的限制，当前的研究仍处于理论验证阶段，后续对实验设备进一步完善后，会得到更加符合实际需求的实验结果。