基于MLS-SVR多响应曲面法的FDM参数优化*
崔庆安,赖旭东
(1.郑州大学管理工程学院,郑州 450001;2.上海海事大学经济管理学院,上海 201306)
0 引言
3D打印是在数据化模型的基础上将数据离散化,通过材料的逐层堆积制造三维实体的新型制造技术[1]。其中熔融沉积制造(Fused Deposition Modeling,FDM)凭借其成本低、操作简单和使用材料范围广等优点[2],在航空航天[3]、生物医疗[4]等诸多领域应用广泛。实践表明,FDM在不同工艺参数水平下,其打印性能有明显差异。尺寸精度、表面质量和打印时间是FDM技术三个重要的性能指标,大量研究对FDM工艺参数与以上指标间的作用关系进行了探索。文献[5-6]运用正交实验法分别评估了各参数对尺寸精度、打印时间和表面翘曲的影响程度和趋势。文献[7-8]运用响应曲面法分别对表面翘曲、尺寸精度进行了工艺参数优化。以上研究表明,由于FDM打印材料在成型过程中的不均匀收缩及内部残余应力,导致打印件侧面尺寸误差大、表面翘曲严重,且FDM打印过程由线到面,打印时间长,严重制约了FDM的广泛应用。因此,对尺寸误差、表面翘曲和打印时间进行工艺参数优化具有重要应用价值。
多响应曲面法(Multi-response surface methodology,MRSM)[9]是解决多响应参数优化问题的重要方法。Kasim M S等[10]利用MRSM对FDM进行了多响应参数优化,证明了其在FDM中的有效性。但是传统MRSM通过多项式模型对各响应与因素间的关系进行建模,且通常只保留二次及二阶效应,无法对实际问题中的复杂作用关系有效建模,进而导致优化结果不理想。于是,引入基于数据驱动的非参数建模方法,如神经网络[11]、支持向量机[12]等。其中最小二乘支持向量回归机[13](Least squares support vector regression ,LS-SVR)是在支持向量机(Support vector machine,SVM)的基础上改进而来的算法,其通过把不等式约束转化为等式约束,从而将SVM中的凸二次规划问题转化为线性系统求解问题,极大提高了训练速度。但是标准LS-SVR算法无法处理多响应参数优化这种多输出系统,通常的解决办法是对多个输出分别建立回归模型并进行组合,这种独立建模的方式由于没有考虑各输出间的潜在关联信息,所以建模精度较差[14]。多输出最小二乘支持向量回归[15](Multi-output least squares support vector regression,MLS-SVR)是在LS-SVR的基础上提出的一种多输出回归模型,其在多任务学习(Multi-task learning,MTL)[16]理论的指导下对各输出间的潜在关联信息进行建模,真正意义上实现了多输出回归建模。
本文以FDM多输出复杂系统为研究对象,在利用拉丁超立方抽样设计实验的基础上运用MLS-SVR模型对FDM多输出复杂系统进行多输出建模,然后利用带约束遗传算法对模型进行多响应寻优。从而提出基于MLS-SVR的多响应曲面法对FDM打印过程进行多响应参数优化,以达到同时降低打印件侧面尺寸误差、表面翘曲,约束打印时间的目的。
1 MLS-SVR原理及优化步骤
1.1 最小二乘支持向量回归
LS-SVR通过非线性映射φ(x)将样本集从低维空间映射到高维希尔伯特空间H(维度为nh)中,并在H中构建最优拟合函数,一般函数形式如下:
f(x)=wTφ(x)+b
(1)
其中,x为输入向量;f(x)为函数值;w∈Rnh为权重向量;b∈R为偏置量。
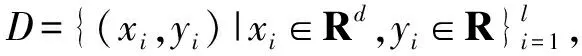
(2)
s.t.yi=wTφ(xi)+b+ξi
(3)
其中,ξ=(ξ1,ξ2,...,ξl)T∈Rl为由松弛变量ξi组成的向量;γ∈R+为正则化参数。式(2)、式(3)的拉格朗日函数为:
(4)
其中,α=(α1,α2,...,αl)T为由拉格朗日乘子αi组成的向量。根据最优解存在的条件,令L分别对w、b、ξ、α求偏导并等于0,可得如下线性方程组:
(5)
其中,K=ZTZ∈Rl×l,Z=(φ(x1),φ(x2),...,φ(xl));其元素Ki,j=φ(xi)φ(xj)=k(xi,xj),k(xi,xj)为满足Mercer定理的核函数;Il为l阶单位矩阵;1I为l维全一列向量。
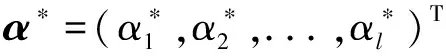
(6)
1.2 多输出最小二乘支持向量回归
标准LS-SVR公式无法处理多输出回归问题,关键是如何对各输出间的潜在关联信息进行建模。MLS-SVR算法在遵循多任务学习的思想下对LS-SVR算法进行推广,其通过将各输出权重向量wi分解为wi=w0+vi来对输出间的潜在关联信息进行建模,即各输出权重向量均在某个均值向量w0周围波动,波动幅度为vm。当输出间关联性较强时,vm趋近于0,反之w0趋近于0。
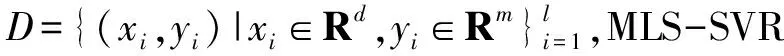
fi(x)=(w0+vi)Tφ(x)+bi
(7)
其中,x为输入向量;fi(x)、(w0+vi)∈Rnh、bi∈R分别为第i维输出的函数值、权重向量和偏置量。在结构风险最小化原则下,MLS-SVR通过最小化如下目标函数来求解w0∈Rnh、V=(v1,v2,...,vm)∈Rnh×m和偏置向量b=(b1,b2,...,bm)∈Rm:
(8)
s.t.Yi,j=(w0+vj)Tφ(xi)+bj+ξi,j
(9)
其中,ξ=(ξ1,ξ2,...,ξm)∈Rl×m,ξi=(ξi,1,ξi,2,...,ξi,l)T为松弛变量组成的向量;Y=(y1,y2,...,ym)∈Rl×m,yi为样本集的第i维输出向量;λ、γ为两个正则化参数。式(8)、式(9)的拉格朗日函数为:
(10)
其中,A=(α1,α2,...,αm)∈Rl×m,αi=(αi,1,αi,2,...,αi,l)T为拉格朗日乘子组成的向量。令L分别对w0、V、b、ξ、A求偏导并等于0,可得如下线性方程组:
(11)
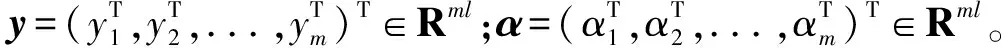
(12)
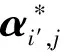
MLS-SVR模型可采用多种形式的核函数,本文采用支持向量机中最为常用的径向基(Radial basis function,RBF)核函数,表达式如下:
(13)
正则化参数γ,λ和RBF核函数宽度系数p为MLS-SVR模型的超参数组合θ=(γ,λ,p),对模型性能有较大影响。
1.3 MLS-SVR多响应曲面法优化步骤
本文运用MLS-SVR多响应曲面法优化FDM工艺参数。主要步骤如下:
(1)确定变量:确定响应变量y1、y2及约束变量y3,选定待优化工艺参数及实验域。
(2)实验设计:利用拉丁超立方抽样(Latin hypercube sampling,LHS)抽取样本点,根据所得样本点安排实验。
(3)构建MLS-SVR模型:通过网格搜索加留一法确定MLS-SVR模型合适超参数组合θ*={γ*,λ*,p*},然后对模型进行训练,确定MLS-SVR模型。
(4)寻优:利用带约束遗传算法在对模型输出y3进行约束的条件下,对由输出y1、y2组合成的复合响应进行寻优,得到最优参数组合及各输出寻优结果。
(5)验证:对寻优结果进行验证实验,得到优化结果。
2 实验设计
2.1 确定响应、约束变量及工艺参数
根据本文研究目标,分别选取打印件侧面尺寸误差、表面翘曲作为响应变量y1、y2,打印时间作为约束变量y3。通过参考相关文献[17-18]及打印机的设置说明,本文所研究工艺参数及实验域如表1所示。

表1 待优化参数及实验域

续表
2.2 LHS实验设计
本文运用LHS抽取样本点,抽样数量为60,根据所得样本点安排实验。实验使用尺寸为35×25×3 mm的长方体打印件,打印设备采用喷嘴直径为0.4 mm的极光尔沃Z-603SFDM打印机。
2.3 实验结果测量
(1)尺寸误差y1:首先,分别测量打印件长度、宽度方向的上下表面尺寸,得到两个方向的最大测量尺寸xLMAX、xWMAX。然后,用游标卡尺外测量爪有斜坡部位分别测量长度、宽度方向4个侧面的中部位置尺寸,得到四个侧面的最小测量尺寸xLMIN1、xLMIN2、xWMIN1、xWMIN2。最后以打印件实际尺寸与设计尺寸xL=35 mm、xW=25 mm的总相对误差∂来代表尺寸误差y1的大小,单位为‰,计算公式如下:
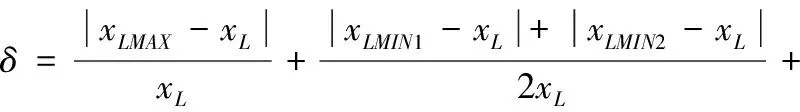
(14)
(2)翘曲y2:如图1所示,用数显游标卡尺测出翘曲最大所在底面长度方向的边缘曲线到其水平切线的最大翘曲量,作为翘曲y2的大小,单位为mm。

图1 翘曲测量示意图
(3)打印时间y3:采用秒表加运动相机测量打印过程的时间间隔,作为打印时间y3的大小,单位为s。
3 实验结果分析
3.1 模型拟合
得到60组LHS样本点及实验结果后,从中随机抽取10组做测试集,其余50组构成训练集。由于各变量间量纲不同,故统一归一化到[0,1]区间。
以各样本点x1、x2、x3、x4、x5、x6作为输入向量,y1、y2、y3作为输出向量,构建MLS-SVR模型。首先采用网格搜索法在初始网格γ∈{2-5,2-3,...,215}、λ∈{2-10,2-8,...,210}、p∈{2-9,2-7,...,23}中搜索最优超参数组合,对于每一超参数组合,通过在训练集上运用留一法,计算其在各验证集上各输出实际值和拟合值的总体平均方差,以总体平均方差最小为标准确定初始网格下的最优超参数组合。然后采用等距细网格搜索在上步所得最优超参数组合附近重复上述步骤,最终寻得θ*={2,2,0.635}。最后用训练集数据对模型进行训练,确定MLS-SVR模型。
对MLS-SVR模型多输出拟合效果及各输出残差进行检验,图2为样本集上各输出拟合值和实际值的散点图,各输出的拟合值均匀分布在红色线(45°对角线)附近。图3为样本集上各输出残差和实验顺序散点图,各输出残差在水平轴附近无规则地随机波动,与实验顺序无关。图4为样本集上各输出残差和拟合值散点图,各输出残差无明显异常模式。以上结论表明,MLS-SVR模型有效拟合了各参数对尺寸误差、翘曲和打印时间的作用关系,建模效果显著。
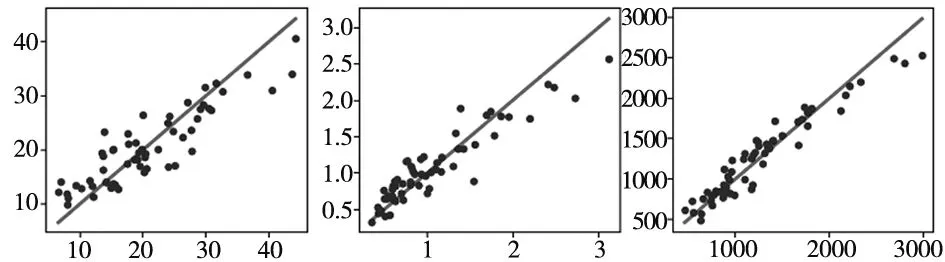
(a) 尺寸误差% (b) 翘曲mm (c) 打印时间s图2 各输出拟合值(y)和实际值(x)散点图
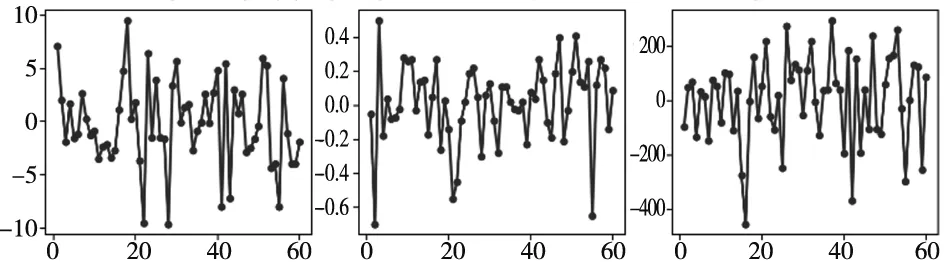
(a) 尺寸误差% (b) 翘曲mm(c) 打印时间s图3各输出残差(y)与实验顺序(x)散点图
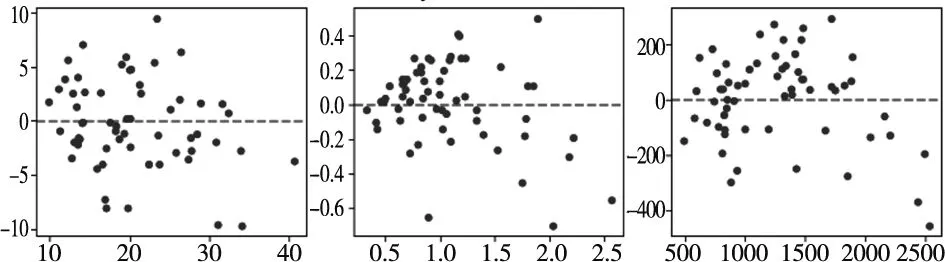
(a) 尺寸误差% (b) 翘曲mm(c) 打印时间s图4 各输出残差(y)与拟合值(x)散点图
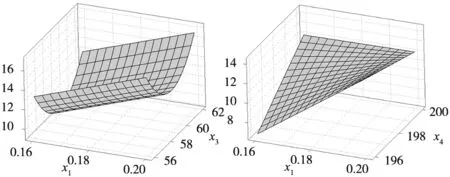
利用MLS-SVR模型可得到15组各参数交互作用对三个输出的曲面图,由于篇幅限制,本文只列出其中两组,如图5所示。可以看出,各参数对三个输出的作用关系复杂,交互效应明显。且各参数对尺寸误差和翘曲的交互作用图比较相似,对尺寸误差、翘曲的实验结果进行相关性检验,得两者相关系数为0.718,P值为0.000,说明两输出间相关性高度显著。因此,对各参数与尺寸误差、翘曲和打印时间的作用关系进行多输出建模时,所选模型须充分考虑各输出与输入间复杂关系和各输出间相关性的影响。
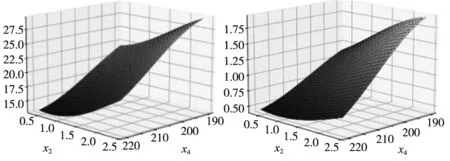
(a)壁厚-喷嘴温度与尺寸误差 (b)壁厚-喷嘴温度与翘曲
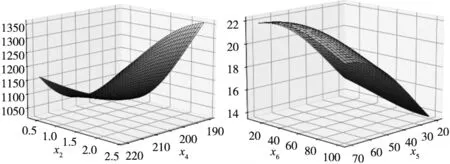
(c) 壁厚-喷嘴温度与打印时间 (d) 打印速度-填充率与尺寸误差
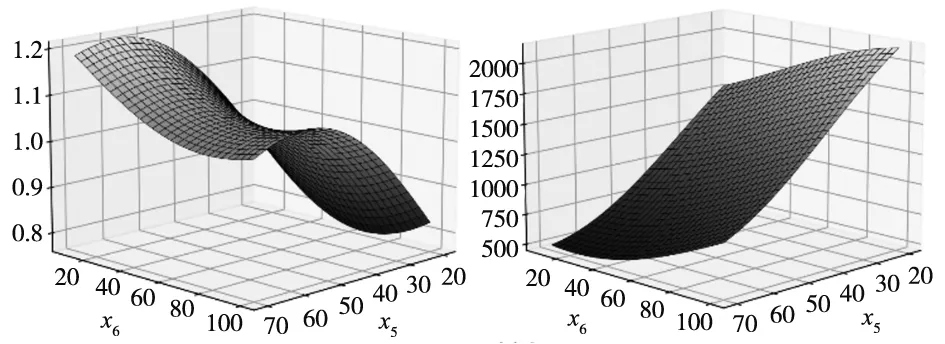
(e) 打印速度-填充率与翘曲 (f)打印速度-填充率与打印时间图5 MLS-SVR多响应曲面法部分曲面图
3.2 参数优化与实验验证
为了实现对打印时间输出进行约束且对尺寸误差、翘曲输出同时寻优,本文对传统遗传算法目标函数进行如下修改:
(1)将响应变量尺寸误差、翘曲通过加权平均整合为单一复合响应,对复合响应寻优。
(2)当打印时间输出值大于约束边界t0时,在其目标函数中添加关于打印时间的惩罚项|y3-t0|,从而在寻优时将打印时间输出约束在[0,t0]的范围内。
修改后遗传算法目标函数表达式如下:
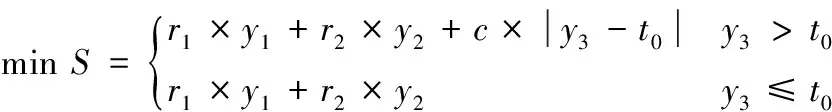
(15)
其中,c为惩罚系数;r1,r2分别为y2,y2的权重,r1+r2=1。由上述遗传算法,取约束边界t0=1173 s(实验结果中位数),权重r1=r2=0.5,惩罚系数c=0.5,种群个体数量为200,寻优过程如图6所示。
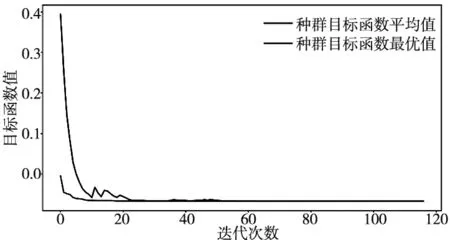
图6 寻优过程图
图6显示,迭代60次左右时,种群逐渐收敛,最终在117代寻得最优参数组合如表2所示。

表2 最优参数组合
利用MLS-SVR模型得到最优参数组合下尺寸误差、翘曲预测值分别为3.589‰、0.194 mm。在该组合下进行三次重复验证实验,尺寸误差验证结果为3.54‰、3.77‰、3.83‰;翘曲验证结果为0.17 mm、0.17 mm、0.19 mm。约束变量打印时间预测值为1173 s,位于约束边界上,验证结果为1160 s。打印件优化前后效果对比如图7所示。

(a) 优化前(b) 优化后图7 优化效果对比图
3.3 传统多响应曲面实验
在同样条件下利用传统MRSM对尺寸误差和翘曲进行优化。由于传统MRSM无法设置约束变量,为了实现打印时间约束条件一致,本文在实验过程中以打印时间t≤1173 s为条件,如果超出,停止实验。
首先进行因子实验,得到尺寸误差和翘曲实验结果,并将其标准化数据通过加权平均整合成复合响应,对复合响应建模得到其多项式。然后用拉格朗日乘数法求解复合响应最优下降路径并进行下降实验,得到复合响应最优区域。然后采用中心复合有界(CCI)设计在最优区域附近进行多响应曲面实验设计,得到尺寸误差和翘曲实验结果并进行逐步回归得到各自二次多项式。最后利用响应优化器在二者权重比1:1、重要度比1:1的条件下对尺寸误差和翘曲进行优化,得到最优预测值分别为7.328‰,0.581 mm。在所得最优参数组合下进行验证实验,尺寸误差验证结果为7.62‰、8.23‰、8.94‰;翘曲验证结果为0.54 mm、0.6 mm、0.68 mm,均在其95%置信区间内。该参数组合下打印时间验证值为623 s,没有超出约束边界。
尺寸误差显著因子为层厚、热床温度、喷嘴温度,翘曲显著因子为层厚、壁厚、热床温度、喷嘴温度。由于篇幅限制,本文只给出部分显著因子对尺寸误差和翘曲的交互作用曲面图,如图8所示。
(a) 层厚-热床温度与尺寸误差 (b) 层厚-喷嘴温度与尺寸误差
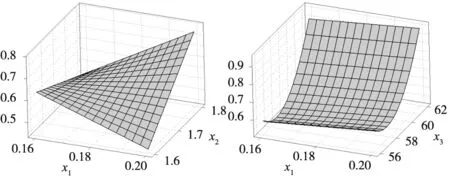
(c) 层厚-壁厚与翘曲(d) 层厚-热床温度与翘曲
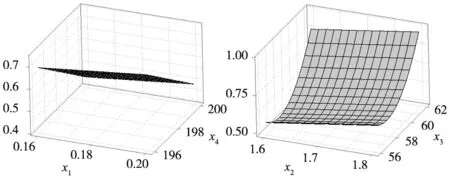
(e) 层厚-喷嘴温度与翘曲 (f) 壁厚-热床温度与翘曲图8 传统MRSM部分曲面图
4 结果分析
(1)优化结果对比
由表3可知,在打印时间t≤1173 s的约束条件下,MLS-SVR多响应曲面法的尺寸误差、翘曲优化结果分别为3.71‰、0.177 mm,同传统MRSM相比,尺寸误差减少53.39%、翘曲减少71.13%,优化效果更好。另外,本文所提方法打印时间约束结果为1160 s,预测值为1173 s,处于约束边界上。说明由于约束条件的限制,尺寸误差和翘曲还未达到最小值,同时说明所提方法有效约束了打印时间。
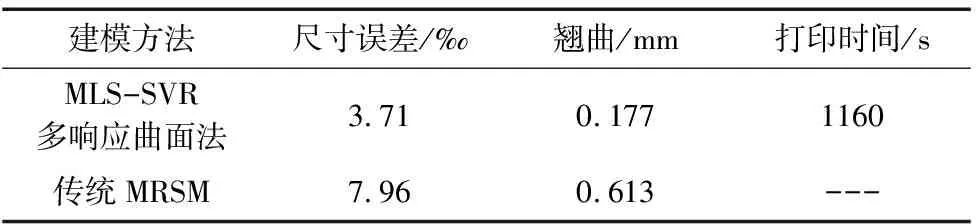
表3 优化结果对比
(2)实验过程对比
本文实验过程中,MLS-SVR多响应曲面法共用60次实验。传统MRSM经过部分因子、最速上升、全因子和CCI实验,共用76次实验。本文所提方法比传统MRSM节省了16次实验,且实验步骤更加简单。另外,传统MRSM优化结果受部分因子实验初始点的影响,容易陷入局部最优。而本文所提方法利用LHS在实验域均匀分布样本点,可更加全面、有效地代表样本空间。
(3)建模能力对比
两种方法对FDM多输出复杂系统的建模能力可通过对比图5和图8得出结论。明显看出,MLS-SVR多响应曲面法的交互作用曲面图比传统MRSM的更加复杂,说明MLS-SVR模型充分挖掘了输入与输出及各输出间的关联信息,比多项式模型更加准确、全面地模拟了多输出系统内的复杂作用关系,建模能力更强。
5 结论
本文以FDM多输出复杂系统为研究对象,提出基于MLS-SVR的多响应曲面法对其进行了参数优化,并与传统MRSM进行了比较,得出以下结论:
(1)同多项式模型相比,MLS-SVR模型对FDM多输出系统内复杂作用关系的建模能力更强,且在同时对多个输出进行回归建模的情况下考虑各输出间的潜在关联信息,较适合对现实生产中的多输出复杂系统进行建模。
(2)同传统MRSM采用最速下降法对复合响应进行寻优相比,本文所提遗传算法对复合响应的全局优化能力更强,且可以解决有约束问题,寻优策略更加多样,可有效对模型各输出进行优化和约束。
(3)同传统MRSM相比,本文所提方法采用MLS-SVR模型和带约束遗传算法对FDM多输出复杂系统进行全局建模和优化,实验步骤更加简单,建模效率更高,优化效果更好。

