混凝土圆形筒仓群不同工况下计算分析的对比研究

王煜成（上海市建筑科学研究院有限公司，上海 200032）

混凝土筒仓群由于其力学性能优异、存储模式多样化，目前已广泛应用于食品、化工等行业中。随着设计、施工技术不断更新，筒仓之间形成的星仓往往成为备用存储空间，因此起控制作用的装料工况除传统的筒仓装料工况外，还有星仓装料而周边筒仓空仓的工况。GB 50077—2017《钢筋混凝土筒仓设计标准》规定，仓壁相连的圆形群仓，除按单仓计算外，尚应在空、满仓不同荷载条件下对仓壁相接处的内力进行验算，可使用程序亦可采用附录 G 的公式；但规范并未对二者验算结果不一致时给出相关规定。

本文以某单筒φ22 m、高 41 m 的 3 m× 4 m 筒仓群为例，对不同的装料工况分别采用有限元程序和规范公式进行计算，对二者计算结果进行对比；并分析了二者计算结果存在差异的原因，为筒仓群在不同工况下的设计及安全复核提供参考。

1 筒仓群建筑结构概况

该筒仓群为钢筋混凝土圆形群仓，单仓外径 22.0 m，排列形式为 3 m×4 m，共 12 个单仓，以相邻仓壁和筒壁外圆相切的方式连接，圆形筒仓之间共形成 6 个星仓。筒仓总高度 41.0 m，共分为 2 F。1 F 为仓底区域，层高 4.7 m，主要为卸料以及向外运输储粮的工作空间。2 F 为装粮筒仓，层高 36.3 m。

筒仓单仓设计仓容为 6 500 t，星仓单仓设计仓容为1 500 t，总仓容为 87 000 t。筒仓主体仓壁采用钢筋混凝土结构，结构安全等级为二级，地面以上结构的环境类别为二（a）类，抗裂等级为三级。

筒仓壁自下而上厚度均为 250 mm，仓底平台下方采用钢筋混凝土框架梁、框架柱以及筒壁共同支撑；筒仓相接处设置混凝土腋角，腋角单边宽度为 1 500 mm。

筒仓仓壁和顶板的混凝土强度等级为 C 30，钢筋类型均为 HRB400，仓壁保护层厚度为 30 mm。仓壁环向配筋为双侧配筋，单侧钢筋规格在 C 12～C 22 之间，钢筋间距在130～200 mm 之间；纵向钢筋为双侧配筋，单侧钢筋规格为 C 12 和 C 14，钢筋间距均为 200 mm。

2 不同工况下仓壁荷载计算

由于筒仓高宽比较小，风荷载在此条件下对结构受力特性影响较小，计算时不考虑风荷载作用。由于仓壁与仓底整体连接，根据 GB 50077—2017 要求，可不对仓壁进行抗震验算。由于装料高度与筒仓直径之比较低，计算时不考虑偏心卸料影响。根据 LS 8001—2007《粮食立筒库设计规范》要求，对于一般装粮筒仓，计算时不考虑温度作用。

2.1 贮料荷载计算

在不考虑风荷载、温度作用、地震作用的情况下，筒仓验算的主要荷载为恒荷载、屋面活荷载以及贮料荷载。本工程装料主要为小麦，设计容重约为 5.2 kN/m3，根据设计仓容可得筒仓单仓的贮料高度为 35 m，星仓单仓的贮料高度为 28 m。

由于贮料的物理特性，贮料在重力流动压力的作用下会与仓壁产生一定的摩擦。依据国家标准 GB 50077—2017，贮料对于仓壁和仓底存在以下 4 种作用力。① 仓壁的侧向压力ph。② 仓壁的竖向摩擦力pf。③ 仓底漏斗的法向力pn。④ 仓底漏斗的摩擦力pt。具体如图 1 所示。

图1 深仓贮料压力示意图

本文中筒仓底部均为平底，星仓底部设有混凝土建筑找坡而非漏斗式仓底，贮料的仓底压力绝大部分由下部混凝土梁柱承受。影响仓壁承载力的主要贮料荷载即为仓壁的侧向压力ph和仓壁的竖向摩擦力pf。

依据 GB 50077—2017，对于高径比 ≥1.5 的圆形深仓，作用于仓壁单位面积上的水平压力ph和作用于仓壁单位周长上的总竖向摩擦力pf的计算公式如式（1）、式（2）所示。

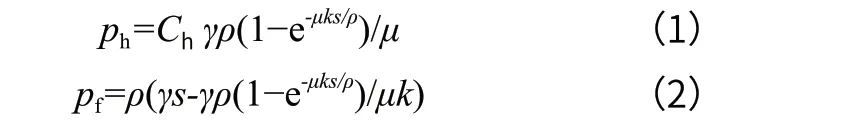
式中：Ch—贮料水平压力修正系数；

γ—贮料的重力密度，kN/m3；

ρ—筒仓水平净截面的水力半径，m；

μ—贮料对仓壁的摩擦系数；

k—侧压力系数；

φ—贮料的内摩擦角，（°）。

对于本项目中的小麦，不同工况下不同高度处的贮料压力计算结果如表 1 所示。

表1 不同高度的贮料荷载计算结果

2.2 群仓装料计算工况

本工程为群仓，单个筒仓的空仓或满仓对结构受力影响较大。相对全仓满仓状态，部分仓为空仓时，仓壁受力工况更多，结构受力更不利。本文选取两种不同的荷载布置形式进行计算分析。具体如图 2、图 3 所示。

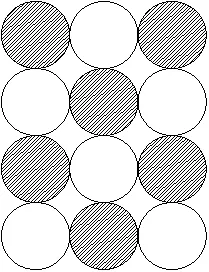
图2 筒仓为间隔装料的贮料荷载布置示意图（填充为装料部分）

图3 星仓装料的贮料荷载布置示意图（填充为装料部分）

3 程序计算结果

计算程序采用盈建科建筑结构设计软件 YJK 1.9.2 的筒仓设计模块。筒仓仓壁采用壳单元进行模拟，加腋区刚度采用在腋角边缘增加墙体的方式来模拟，并将仓底（标高 4.7 m）作为上部筒仓的嵌固部位。根据筒仓实际配筋的区段，将壳单元沿高度方向分成多个区段。

仓顶恒荷载以及设备活荷载等按照实际情况施加，贮料荷载由程序自动生成每段的贮料法向压力和竖向摩擦力，贮料荷载按照前文所述分为筒仓间隔装料和星仓装料两种工况施加，程序自动按照包络值进行计算。

程序计算典型内力结果如表 2 所示。可见无论是筒仓间隔装料还是星仓装料，仓壁在侧向压力的作用下主要承受轴力，腋角处承受一定的环向弯矩。

表2 程序计算典型内力结果

程序根据包络内力结果自动进行配筋计算。计算结果表明，筒仓间隔装料的工况更为不利。此工况下仓壁环向配筋最大值出现在仓壁底部，竖向钢筋配筋均为构造配筋。对仓壁实际配筋结果进行复核，复核结果如表 3 所示。复核结果表明，采用程序计算时，实配钢筋面积大于计算值，仓壁承载力满足要求。

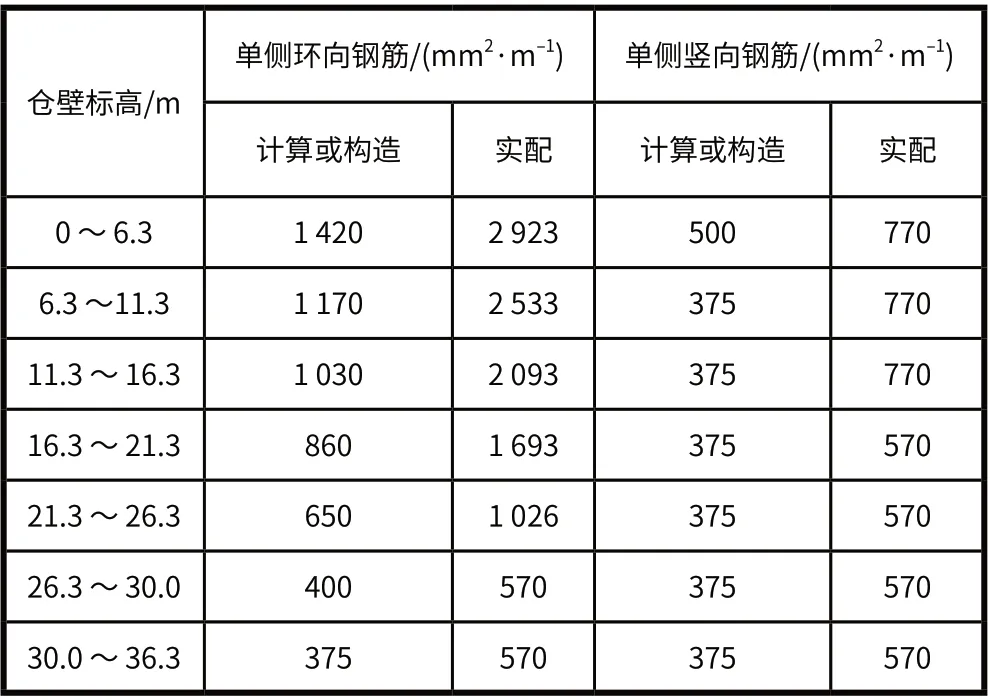
表3 典型仓壁配筋程序计算结果

4 规范公式计算结果

GB 50077—2017 的附录 G 给出了不同工况下星仓仓壁受力的计算公式。工况一为星仓装料且筒仓空仓，工况二为筒仓间隔装料且星仓空仓。计算如图 4、图 5 所示。

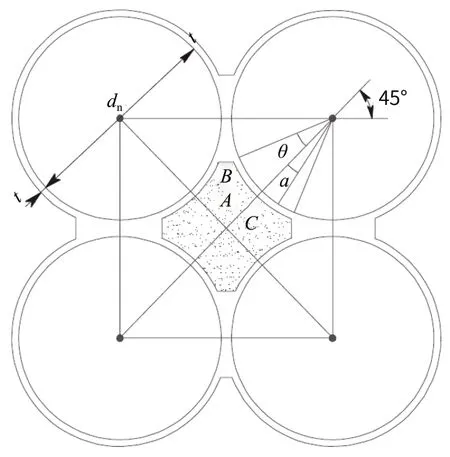
图4 星仓装料工况规范公式计算示意图

图5 筒仓间隔装料工况规范公式计算示意图

星仓装料且筒仓空仓工况下，仓壁不同位置的内力计算公式如式（3）～式（6）所示。

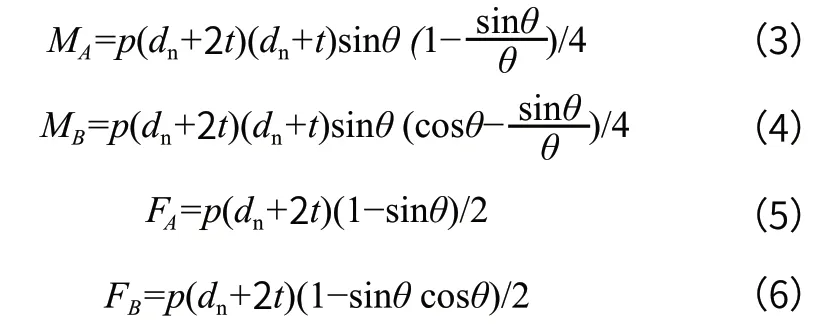
式中：p—贮料侧压力，kPa；

dn—圆形筒仓的内径，m；

t—仓壁厚度，m；

θ—腋角边缘（B点）和星仓仓壁中部（A点）之间形成的圆弧夹角，（°）。

筒仓间隔装料且星仓空仓工况下，仓壁不同位置的内力计算公式如式（7）～式（10）所示。

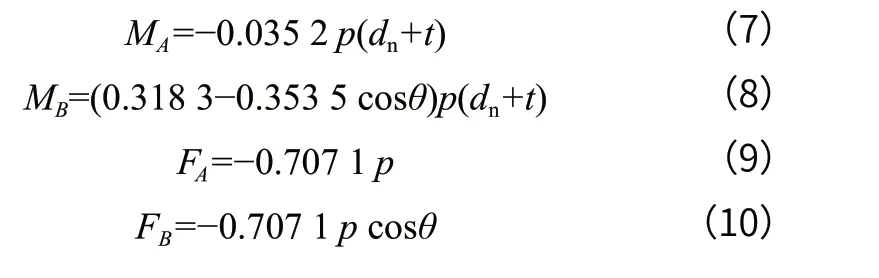
由此可见，筒仓仓壁在水平平面内均表现为压弯构件，将仓壁竖向剖面等效为偏心受压柱的横截面即可计算出仓壁所需的环向配筋。本文中筒仓腋角宽度为 1 500 mm，夹角θ=37°。将参数代入上述公式计算出不同工况下的仓壁内力结果和环向配筋结果如表 4 所示。

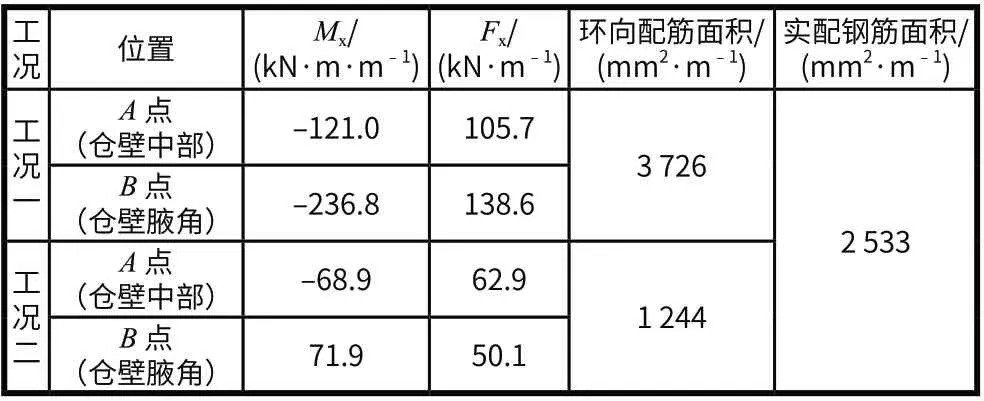
表4 不同装料工况规范公式仓壁内力计算结果

计算结果表明，工况一（星仓装料且筒仓空仓）的仓壁在腋角处受力特性最为不利，腋角处承受了较大的平面内弯矩，导致环向钢筋计算面积超出了原设计单侧环向钢筋配筋面积，仓壁承载力不足。

5 不同计算方式的对比分析

根据前文的计算结果，程序计算时控制工况为筒仓间隔装料的工况，而规范公式计算时控制工况为星仓装料的情况，说明程序计算和规范公式计算的主要区别在星仓装料这一特殊工况。

星仓装料而周边筒仓空仓时星仓两侧的腋角可视作仓壁的侧向支座，此时星仓仓壁为同时承受压力、剪力、弯矩的相似拱，其受力状态与支座的位置和支座刚度有直接关系。由于此种工况下仓壁受力状态复杂，所以各国学者都以不同的假定条件提出不同的计算方法。

目前星仓仓壁内力的理论计算方法主要包括 3 种。第一种是将星仓腋角视为固定支座，具有代表性的是 Timm 和Mindels 法。第二种是将星仓腋角视为滑动支座，具有代表性的是 Safarian 和 Harris 法。第三种是考虑了星仓周边筒仓的侧向刚度的共同作用，具有代表性的是 Ciesielski 法。当腋角视作固定支座时，星仓仓壁主要承受轴向压力，弯矩较小；当腋角视作滑动支座时，星仓仓壁则主要承受弯矩，腋角处轴力为 0。考虑筒仓共同作用时内力的计算结果在两者之间。HAYDL H M[1]、BA L C 等[2]、YUKSEL S B[3]、YUKSEL S B 等[4]分别利用平面单元、实体单元对星仓装料工况进行模拟，并与上述三种理论计算结果进行对比。对比结果表明，无论是平面单元还是实体单元，有限元模拟的结果均与 Ciesielski 法较为接近。

GB 50077—2017 附录 G 的条文说明指出，我国规范采用的 Kellner 法计算结果较 Ciesielski 法小，但仍略大于波兰粮仓规范和前苏联粮仓规范。通过权衡公式操作应用的便捷性和内力计算的可靠性，最终选择了 Kellner 法作为附录G 的计算公式。

但是，上述理论计算公式以及有限元模拟结果针对的对象均为平面薄片状的筒仓群。换言之，实际筒仓仓底和仓顶对仓壁侧向变形的约束作用并未充分考虑。王广国等[5]介绍了一种考虑仓底（顶）约束作用的空间分析方法，考虑了筒仓高径比H/R的作用，当高径比较小时，星仓仓壁腋角处的弯矩将大幅降低。事实上，星仓装料时内力最大处位于星仓底部，此时底板对仓壁、腋角的侧向约束效应相比较于筒仓中部更大，仓底的腋角相比较于筒仓中部的腋角更接近于固定支座。根据已有分析结果，此时星仓仓壁应当更接近于轴压构件而非压弯构件，因此建立考虑仓底和仓顶侧向刚度的三维空间模型的计算结果相对更加合理。

本文的计算模型采用壳单元对加腋进行模拟，如果采用实体单元建模计算结果会更加准确，然而在实际工程应用中，通过精细化建模模拟腋角、仓底、仓顶的侧向刚度通常难以实现，此时采用规范公式得到一个相对保守的结果是简便且可行的。在筒仓设计或复核咨询过程中，当程序计算结果与规范结果相差较大时，可以通过适当增大腋角宽度大幅降低腋角处的弯矩，减少配筋量的同时也不会占用过多的仓容，是一种简便可行的操作方法。

6 结 语

(1) 星仓装料而周边筒仓空仓的工况下，使用程序计算的配筋结果小于规范公式的配筋结果，主要是由于腋角刚度以及仓底侧向约束作用考虑程度不同导致。

(2) 从实际工程角度出发，星仓装料工况下采用规范公式是一种相对简单保守的做法。如程序计算结果与规范结果相差较大时，建议适当增加腋角宽度以降低仓壁最不利处的弯矩。