机器人磨抛工艺参数优化方法研究
田凤杰,狄春东,韩 晓,李 论
(1.沈阳理工大学 机械工程学院,辽宁 沈阳110159; 2.中国科学院 沈阳自动化研究所,辽宁 沈阳110016)
磨抛属于精加工工序,一般作为加工过程的最后一道工序,可以有效地提高工件表面的加工质量。工业机器人的操作空间灵活且价格便宜,广泛应用于磨抛领域。在磨抛过程中,工件表面质量是衡量机器人磨抛效果的重要标准,磨抛去除率是衡量机器人磨抛效率的重要标准。如何选择加工参数组合来同时保证去除率和工件表面质量,是急需解决的问题[1-2]。
技术人员的大量研究表明:以接触应力和磨削工艺参数作为输入,基于Thunder GBM算法建立的材料去除率预测模型,具有较高的准确性与有效性[3];通过建立钛合金磨抛加工表面粗糙度二阶预测模型,能对工艺参数进行优化[4];采用灰色关联分析法确定加工参数,要得到最优解仍然需要大量试验[5]。综上所述,大多数研究只满足去除效率或者表面质量的单一情况来求取最优的参数组合,或者通过灰色关联分析等算法建立模型求得最优参数组合,但仍需要进行大量试验,成本较高,加工周期长,目前还没有成熟的机器人磨抛工艺参数优化方法,既保证加工表面质量又能保证磨抛去除率。
针对以上问题,本文研究各工艺参数对加工后表面粗糙度和磨抛去除率的影响关系,建立表面粗糙度和磨抛去除率的线性回归方程,运用NSGA-Ⅱ算法确定最优的加工参数组合,同时保证加工效率和工件的表面质量。
1 理论分析
1.1 磨抛去除率模型
砂带上的磨粒形状各异,一般呈锥形、菱形等,为方便计算,把磨粒简化为尖端带圆弧的锥形。磨粒在砂带上的高度服从高斯分布,如图1所示。

图1 磨粒分布
磨粒突出高度为h;最大磨粒高度为dmax;最小磨粒高度为dmin;标准差为σ;磨粒高度的平均值为dm,dm=(dmax+dmin)/2。坐标系的原点0位于磨粒高度为dm之处,磨粒切入深度d=h-h0。磨粒高度大于3σ的部分占比小于0.15%,可忽略不计。
当|h|<3σ时,磨粒突出高度分布函数为[6]:
(1)
单位面积上磨粒总数为N0,单位面积上有效磨粒数量为:

(2)
磨粒切入分为3种情况:当磨粒切入深度没有超过最大弹性变形量δmax时,只发生弹性变形;当磨粒切入深度超过最大弹性变形量δmax时,发生塑性变形,塑性变形分为两种情况:切入深度小于切削刃半径R;切入深度大于R。3种情况对应的力与磨抛深度关系为[6]:
(3)
(4)
(5)
式中:E*为磨粒与工件的接触弹性模量;R为磨粒顶端的切削刃半径;α为磨粒切刃顶角;δ为工件的变形量;HB为工件硬度。3种情况均表明,随着磨抛力的增大,切入深度也逐渐增大。
工件磨抛过程如图2所示。
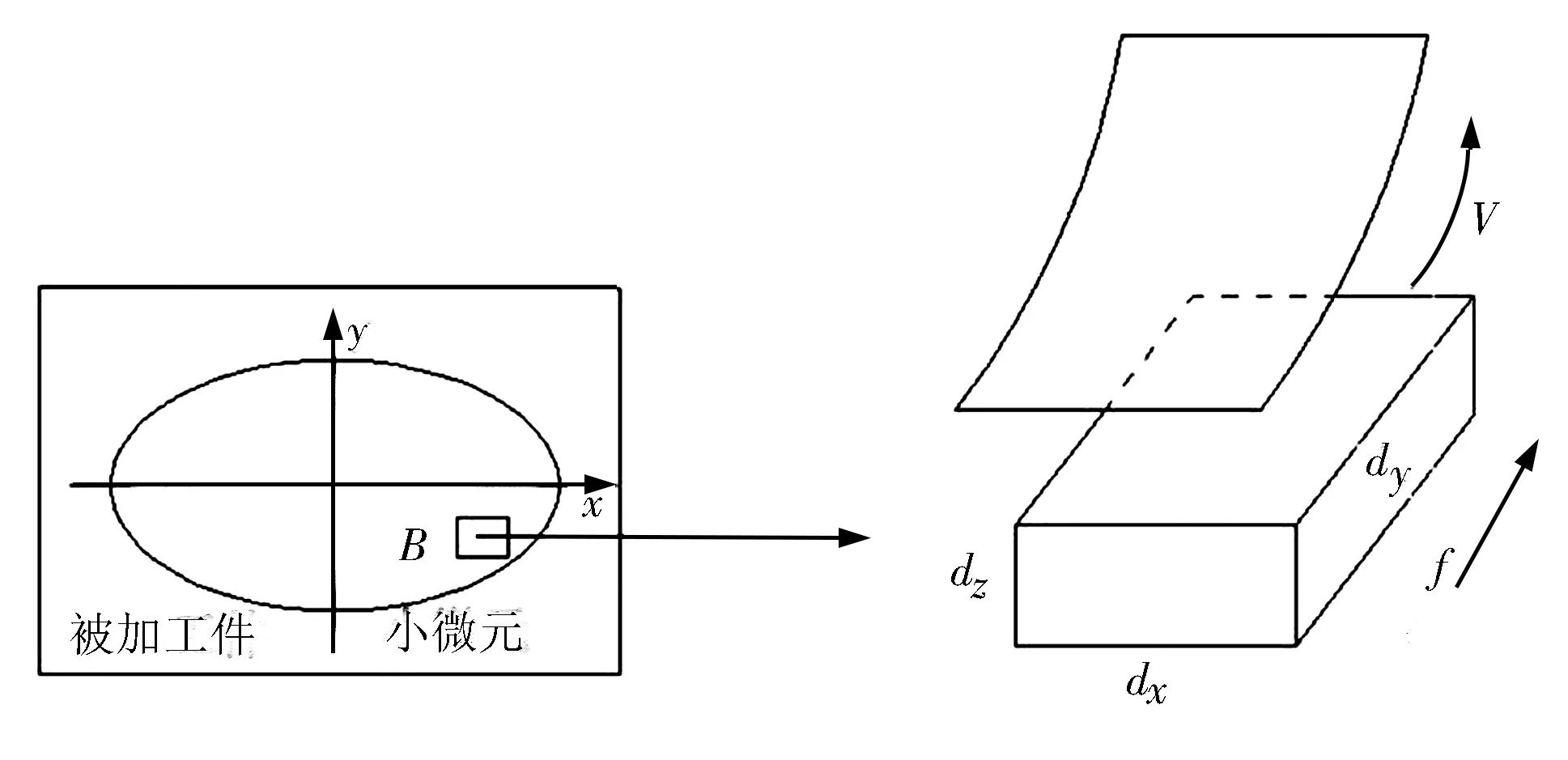
图2 工件磨抛过程
B为工件表面位置的小微元(长dy,宽dx),其面积为dydx,与微元B接触时间为dt,f为加工方向的进给速度,dt=dy/f,V为砂带的磨抛速度,该时间对应的砂带接触面积为:
S=dydxV/f
(6)
研究表明,由于砂带存在弹性变形,实际的切削深度d0与理论切入深度d并不相等,一般成比例关系。可设d0=k1d。其中,k1为比例系数。单颗磨粒去除形状如图3所示。

图3 单磨粒去除形状
单磨粒去除形状近似为三菱柱,单磨粒去除材料体积为:
(7)
在时间dt内,参与磨削磨粒数N2=N1S,去除材料总体积为:
(8)
单位时间内磨抛去除率Q=dW/dt,把式(2)、(6)、(8)代入,得到的单位时间磨抛去除率为:
(9)
由式(9)可得,随着磨抛速度、进给速度的增大,去除率逐渐增大;随着磨抛力的增大,切入深度逐渐增大,去除率也逐渐增大;由式(1)可知,随着粒度号增大,最大磨粒高度、磨粒突出部分高度f(h)逐渐减小,去除率也逐渐减小。
1.2 磨抛粗糙度模型
由粗糙度定义可知,粗糙度为:
(10)
式中,n为测量长度上取样点个数。这里设单位长度上磨粒个数为N,测量长度为dL,测量长度上磨粒数为N×dL,其中dL=V×dt=V×dy/f,磨粒个数即为取样点个数,n=NVdy/f,di为第i颗磨粒切入深度,那么第i颗磨粒切削深度为k1(hi-h0)。将上述参数代入式(10),可得:
(11)
由式(11)可知,随着砂带粒度和磨抛速度的增大,参与磨抛的磨粒数就越多,粗糙度越低;随着进给速度增大,参与磨抛的磨粒数减少,粗糙度逐渐增大;随着磨抛力的增大,磨粒切入深度也逐渐增大,粗糙度则逐渐增大。
2 deform仿真分析
仿真工件为20 mm×20 mm×5 mm的长方体,材料为45号钢,仿真磨抛后表面形貌如图4所示。

图4 仿真磨抛后表面形貌
磨抛工具为砂带的简化模型,上面布满随机分布的陶瓷氧化铝磨粒。用deform软件进行磨抛力、磨抛速度、进给速度、砂带粒度的单因素试验。对仿真后的表面分析计算,求取表面粗糙度和磨抛去除率。
2.1 仿真结果分析
单因素试验的粗糙度和去除率仿真结果与极值如表1和表2所示,对数据进行分析得到:对粗糙度影响从大到小分别是砂带粒度、磨抛力、进给速度、磨抛速度;对去除率影响从大到小分别为磨抛力、进给速度、砂带粒度、磨抛速度。

表1 单因素仿真结果

表2 仿真极值表
根据表1仿真结果绘制各工艺参数对去除率和粗糙度影响的折线图(图5)。分析可知:随着磨抛力、磨抛速度、进给速度的增大,去除率逐渐增大;随着砂带粒度的增大,去除率逐渐减小;随着磨抛力和进给速度的增大,粗糙度逐渐增大;随着磨抛速度和砂带粒度的增大,表面的粗糙度逐渐减小,与推导的理论一致,验证了仿真的准确性。

(a) 磨抛力

(b) 磨抛速度

(c) 进给速度
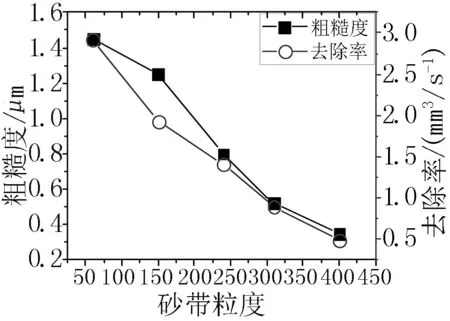
(d) 砂带粒度图5 各工艺参数对去除率和粗糙度影响的折线图
2.2 数据处理
为了找出各参数与粗糙度之间的近似函数关系,采用回归分析方法建立数理统计模型[7]。设表面粗糙度函数方程为:
Ra=k2FaVgfcMz
(12)
式中:k2为粗糙度磨抛系数;F为磨抛力;V为磨抛速度;f为进给速度;M为砂带粒度;a、g、c、z均为回归待定系数。
为了方便求解,将式(12)两边同时取对数得到
lnRa=lnk2+alnF+glnV+clnf+zlnM
(13)
令lnRa=y,lnk2=b0,lnF=x1,lnV=x2,lnf=x3,lnM=x4,a=b1,g=b2,c=b3,z=b4,则对应的线性回归曲线方程为:
y=b0+b1x1+b2x2+b3x3+b4x4
(14)
式中:y为评价指标;x1,x2,x3,x4为4个自变量。代入各组试验数据可建立线性回归方程为:
(15)
矩阵方程可表示为:
Y=Xb+ε
(16)
式中:ε为试验误差;Y为仿真的表面粗糙度值矩阵;X为仿真的参数值矩阵。
该矩阵可表示为:
由最小二乘法可得:
(17)
将仿真数据代入,仿真粗糙度回归方程为
Ra=e2.974F0.343V-0.407 4f0.136 4M-0.634 8
(18)
同理,仿真去除率回归方程为
Q=e1.968 4F0.797 6V0.289 6f0.261 3M-0.769 6
(19)
2.3 求最优解
为了获得同时保证加工质量和加工效率的最优参数组合,采用 NSGA-Ⅱ多目标优化算法解决磨抛工艺优化问题[8],把粗糙度和去除率的回归方程代入求取最优的参数组合。输入的参数范围:磨抛力5~10 N,进给速度6~30 mm/s,磨抛速度6~18 m/s,砂带粒度60~240。算法参数设置:种群大小100,交叉概率0.8,变异概率0.5,进化迭代次数为 10 000。迭代求解Pareto,从图6可以看出最优解是一个范围值,从中选择合适的粗糙度和去除率,该点对应的参数组合就是最优解。

图6 仿真粗糙度和去除率最优解
3 试验验证
3.1 正交试验
以45号钢板为加工材料,以砂带为工具连接在机器人末端,进行磨抛力、磨抛速度、进给速度和砂带粒度的4×3正交试验,如图7所示。各影响因素水平如表3所示。

图7 磨抛试验设备

表3 影响因素水平表
使用电子称和粗糙度仪测量加工前后工件的质量和表面粗糙度。去除率通过测量前后加工质量差与密度和加工时间换算求得,数据结果如表4所示。

表4 正交试验结果
磨抛后的表面形貌如图8和图9所示,编号1-9分别对应表4的9组试验磨抛后的表面形貌。

图9 加工后表面形貌2
对正交试验结果进行均值和极差的计算,如表5所示。
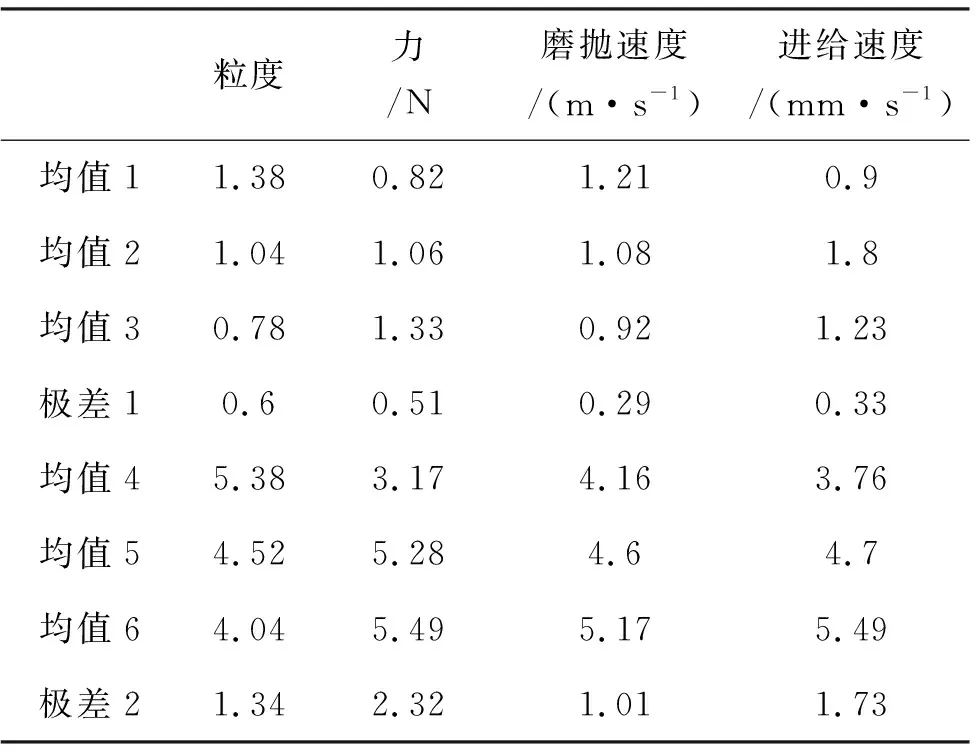
表5 正交试验的均值和极差
均值1、2、3和极差1为粗糙度对应的计算值,均值4、5、6和极差2为去除率对应的计算值,对试验结果分析得到:对粗糙度影响从大到小分别是砂带粒度、磨抛力、进给速度、磨抛速度;对去除率影响从大到小分别为磨抛力、进给速度、砂带粒度、磨抛速度。这与仿真的趋势一致,验证了理论与仿真的准确性,同时也验证了试验结果的准确性。
3.2 数据处理
将数据代入得到试验的粗糙度的回归方程为:
Ra=e1.038 7F0.775 2V-0.366 9f0.164 5M-0.440 3
(20)
试验的去除率的回归方程为:
Q=e-0.442 7F0.792 6V0.181 1f0.226 9M-0.139 7
(21)
表6和表7分别为粗糙度和去除率的预测值与试验值对比,18组对照值中有三个的误差为0.2左右,其余误差都小于0.13,误差在可接受范围内,说明线性回归模型是合理的。

表6 粗糙度误差对照表
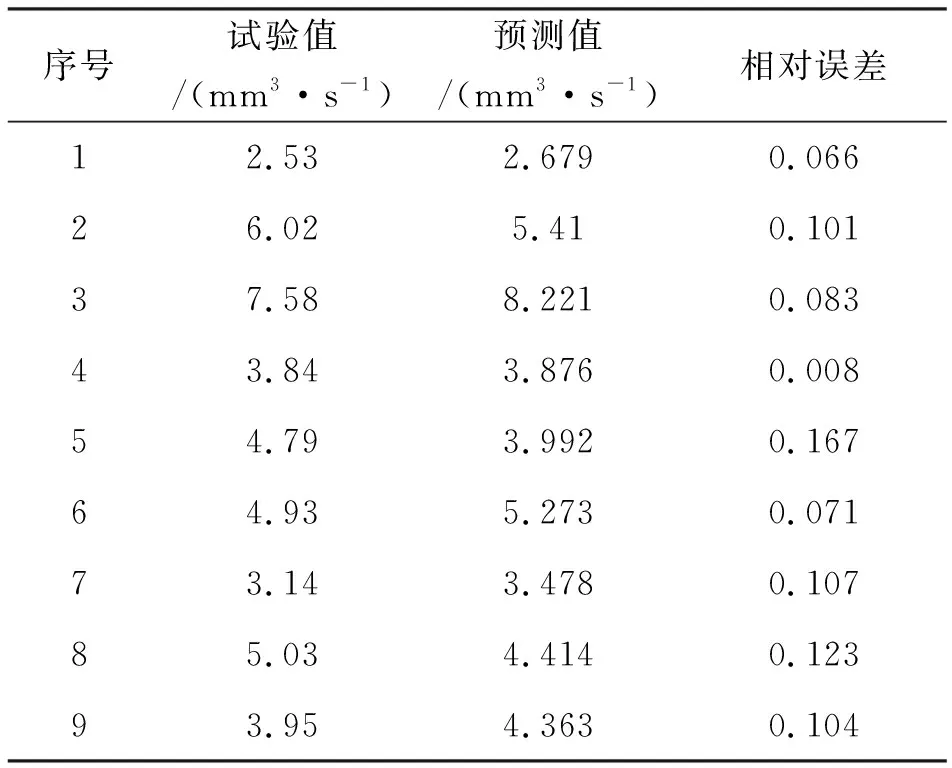
表7 去除率误差对照表
3.3 优化验证
与仿真方法一样,把粗糙度和去除率的回归方程代入求取最优的参数组合,采用 NSGA-Ⅱ多目标优化算法来解决磨抛工艺优化问题,结果如图10所示。

图10 试验粗糙度和去除率最优解
本文选取的参数:磨抛力7.2 N、磨抛速度18 m/s、进给速度18 mm/s、砂带粒度150,加工后的表面粗糙度为0.91 μm,磨抛去除率为4.3 mm3/s,加工后表面如图9中编号10所示。通过此研究方法取得的最优参数组合进行磨抛加工试验,能够达到预期的磨抛去除率和表面粗糙度要求,表面加工质量良好,证明此工艺参数优化方法是可行的。
4 结束语
通过试验对仿真建立的表面粗糙度和磨抛去除率多元线性回归方程进行验证,试验结果显示,18组对照值中有三个的误差为0.2左右,其余误差都小于0.13,误差在可接受范围内,为表面粗糙度和磨抛去除率的预测提供可靠的方法。
以加工后表面粗糙度和材料磨抛去除率方程作为目标函数进行双目标优化,运用 NSGA-Ⅱ算法求解最优参数组合。通过此研究方法取得的最优参数组合进行磨抛加工试验能够达到预期的磨抛去除率和表面粗糙度要求,表面加工质量良好,为机器人磨抛参数的选择提供了方法依据。

