带预应力BGA焊点温循可靠性评估方法研究*

孙 瑜，邵兆申

（1. 移动网络和移动多媒体技术国家重点实验室，广东深圳 518055；2. 中兴通讯股份有限公司，广东深圳 518055；3. 中国空间技术研究院西安分院，陕西西安 710071）

引 言

电子封装在振动、温度循环载荷环境下往往会失效，其中温度循环载荷下因热失配而导致的焊点疲劳失效是电子元件失效的主要原因之一。已有的研究工作多集中在温度循环加载条件下焊料互连的失效机理和疲劳寿命预测模型上。然而某些电子封装装有散热器，关于散热器预应力对封装焊点热疲劳性能的影响研究却相对较少。

本文对某球栅阵列（Ball Grid Array, BGA）封装无铅焊料（SAC305）焊点温度循环可靠性进行了研究。首先对无铅焊料SAC305进行了拉伸测试，拟合了Anand本构的参数，对BGA电子封装设计了温度循环试验装置，完成了有散热器、无散热器两种状态下的−40°C～125°C的温度循环试验及焊点失效监测。建立了电子封装的四分之一对称三维有限元模型进行仿真，仿真得到焊点在−40°C～125°C温度循环载荷下的焊点应变。根据仿真分析结果，利用coffin-manson公式对焊点寿命进行了预测，并与温度循环试验结果进行了比较，分析了装配预应力对焊点热疲劳寿命的影响及预测结果存在偏差的原因。

1 SAC305焊料拉伸试验

近年来，随着无铅焊料的应用，Anand模型也在该焊料上得到应用[1]。对于同一牌号的无铅焊料，不同文献中Anand模型的参数并不相同。本文对所研究的BGA封装及SAC305焊料进行了单轴拉伸测试，明确应变率和温度对SAC305焊料力学性能的影响规律，对测试结果进行处理，得到Anand模型的参数，并用于后续温度循环载荷下的有限元仿真分析。

本文参照金属材料测试标准ASTM E8/E8M，通过加工高纯合金棒，得到哑铃型拉伸试件，标距段为55 mm，可以充分反映材料本身的拉伸力学行为。在相同工况下，进行5组独立的重复试验，以提升试验结果的可靠性。SAC305单轴拉伸试样如图1所示。

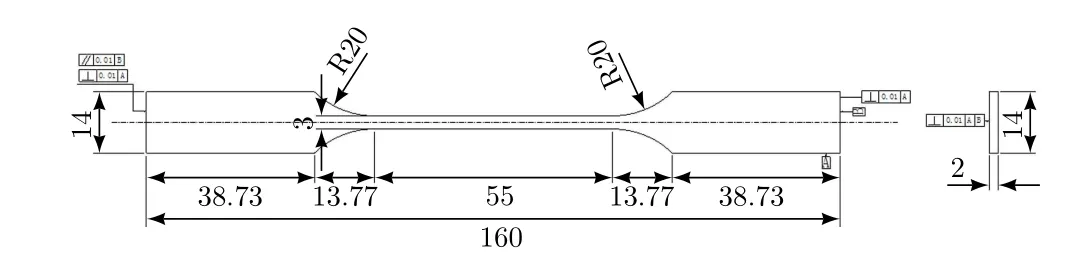
图1 SAC305单轴拉伸试样

拉伸试验共有6个测试温度：−55°C，−10°C，10°C，50°C，90°C，125°C；4个应变率：1×10−4s−1,10×10−4s−1,50×10−4s−1,100×10−4s−1；5组重复试验；共测试试件120件。

2 Anand本构模型拟合

2.1 Anand本构模型

Anand模型的基本方程为[2]：

式中：σ为应力；s为形变阻抗；c是与应变率和温度相关的函数，即：

式中：ξ为应力乘子；εp为非弹性应变；˙εp为非弹性应变率；A为前指数因子；Q为热激活能；R为气体常数；T为绝对温度；σ∗为饱和应力；m为应变率敏感系数；s∗代表在给定温度和应变率下s的饱和值；s0为初始变形阻抗；h0为应变硬化常数；a为应变硬化敏感系数；ˆs和n分别为形变阻抗系数和应变率敏感指数。

2.2 材料常数的确定

根据不同温度及不同应变率下拉伸试验的应力-应变数据可以获得材料常数，其步骤如下：

1）由试验数据得到在不同温度条件下的恒定应变率及其相应的饱和应力数值。

2）根据饱和应力表达式(1)，通过拟合可以得到5个材料参数，即A,Q,m,n和ˆs/ξ。其中前4个参数为定值，最后一个参数随着温度和应变率的变化而改变。

3）根据上一步骤的结果，确定适合的ξ值，以保证c值始终符合条件，即小于1，由此值即可得出各个不同试验条件下的ˆs值。

4）利用各条件下的试验应力-应变曲线与式（5）进行拟合，即可求得ch0,cs0和a值。a取平均值，再次拟合即可得到ch0,cs0两个参数，借助之前已经确定的c值，可以得到单个的h0,s0。

5）最终的h0可以按照式（6）取均值，其中N为试验的个数。

根据不同应变率、不同温度下的试验数据，可以得到Anand模型相关参数，如表1所示。

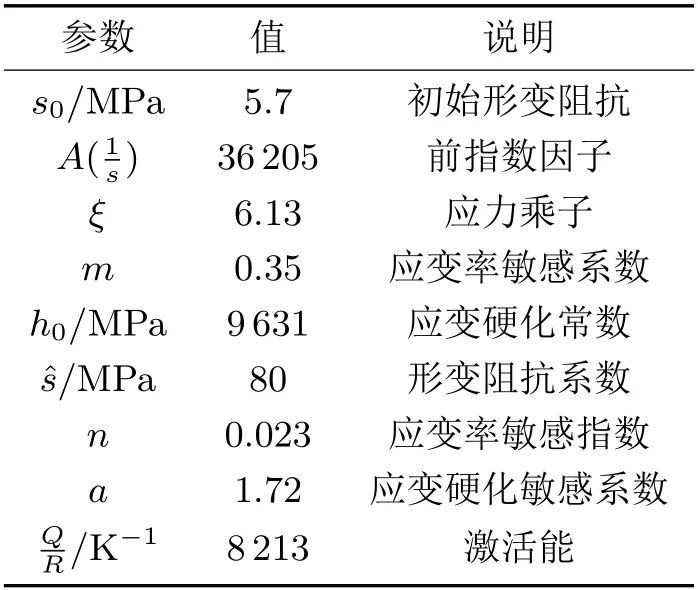
表1 Anand模型参数值

2.3 拟合结果对比

试验数据存在一定的离散性，初始变形阶段的应力-应变曲线斜率偏小且不稳定，但本研究所提出的9参数Anand本构模型依然能够很好地预测温度和应变率对SAC305材料力学性能的影响规律。从图2的试验数据和Anand模型预测的对比情况可知，本研究给出的Anand模型可以很好地体现应变率对材料性能的强化效应和温度对材料性能的弱化效应，随应变增大的应力演化趋势以及饱和应力等关键力学参数与试验结果相符。

图2 SAC305试样不同应变率及温度下仿真与测试结果对比

3 温度循环试验

3.1 试验方法

测试板上焊有BGA器件，BGA设计有菊花链以监测电阻变化。

测试过程中，检测仪器监测菊花链电路在整个测试过程中失效的时间。测试期间，一个焊点中出现裂纹，菊花链的电阻将会增加。失效准则定义为菊花链连续5次电阻较初始值增加20%。

3.2 测试结果

利用上述测试方法进行16个带散热器与4个不带散热器测试板的温度循环（以下简称温循）试验，最大循环次数为800。循环测试结果为不带散热器的4个测试板全部通过800个循环，带散热器的3个测试板的循环寿命在500至800个循环之间，其余测试板全部通过800个循环。以上测试结果为产品设计和仿真分析提供参考。

4 有限元仿真

利用商业软件ABAQUS进行有限元分析，分析了温度循环载荷下器件焊点应力/应变行为，预测了疲劳寿命。仿真分析模型如图3所示，模型中的铜、印制电路板、硅片和焊料都假定为各向同性材料，引线、印制电路板和硅片只考虑它们的弹性变形[3]，在温度循环载荷下仿真分析时，焊料考虑其粘塑性行为，焊料应力-应变关系采用本研究项目的Anand本构模型描述。分析时材料均遵循线弹性假设，详细材料参数见表2。温度循环条件为−40°C～125°C，温变速率为11°C/min,温度保持30 min，一个循环1.5 h，共仿真5个循环[4]。

图3 BGA封装的有限元模型

表2 Anand模型参数值

目前，焊点温度循环失效的寿命模式主要以低周疲劳的Coffin-Manson方程（简称C-M方程）为基础，即材料的低周疲劳寿命Nf和塑性应变范围Δεp符合如下经验关系：

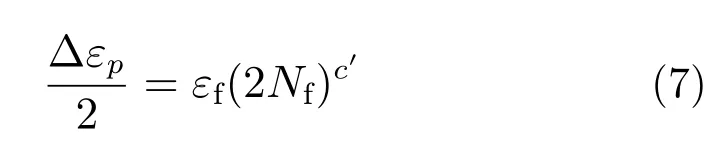
式中：εf为疲劳韧性系数；c′为疲劳韧性指数。由于焊点温度循环、热冲击失效的影响因素很多，在具体应用中，C-M方程被修正成多种形式。同时考虑温度循环温度和频率的影响，C-M方程被修正为[5]：

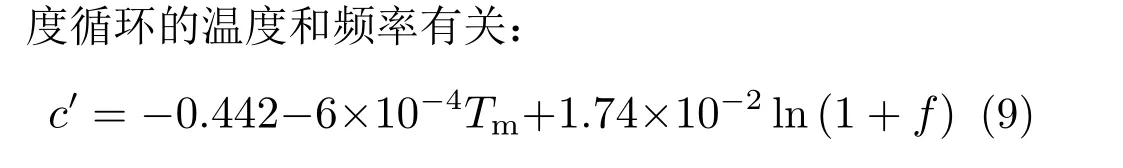
式中：Tm为温度循环的平均温度，Tm= (Tmax+Tmin)/2（Tmax为循环最大温度值，°C；Tmin为循环最小温度值，°C）；f为循环频率。

图4给出了温度循环过程中焊点受力的分布规律。

图4 器件焊点应变云图

由应变云图可知，应变最大的焊点位于器件边角，且该焊点上下表面应变最大。基于Coffin-Manson模型的焊点疲劳寿命分析以器件边角焊点作为寿命预测对象进行寿命预测。其应力-应变迟滞回线如图5所示。

图5 器件角上焊点应力-应变迟滞回线

从图5可以看出，最终等效蠕变应变趋于稳定。从等效蠕变应变-应力迟滞回线中取第5个温度循环周期中应变最小值0.046、应变最大值0.06、应变变化值0.014，根据修正后的Coffin-Manson方程，计算器件焊点寿命为1 300个循环。

从散热器螺钉预载荷下（散热器每个螺钉48 N，共4个螺钉）的仿真结果中取第5个温度循环周期中应变最小值0.053 22、应变最大值0.068 58、应变变化值0.015 36，计算焊点寿命为1 040个循环。其应力-应变迟滞回线如图6所示。从是否带散热器的温循仿真结果对比可以看出，带装配预应力条件下焊点寿命有所降低，这是由装配过程中焊点引入预拉伸载荷所致。

从仿真结果和测试结果的对比可以看出，仿真得到的焊点寿命较高，这是因为仿真分析模型中没有考虑焊点尺寸偏差、焊点空洞缺陷、IMC层厚度等因素的影响，这些因素会对焊点寿命产生较大影响[6]。

5 结束语

实测并拟合得到了SAC305焊料的Anand本构模型参数，应用有限元仿真软件ABAQUS预测拉伸样件应力-应变曲线，将其与试验数据曲线相比较，两者结果基本吻合，验证了参数的有效性。

仿真及测试对比了散热器装配对BGA焊点热疲劳寿命的影响，通过BGA封装温度循环仿真准确模拟了焊点失效风险位置及散热器预应力对焊点热疲劳寿命的影响趋势。分析结果表明，安装散热器引入了拉伸预应力，因而降低了焊点寿命，后续产品设计过程中应关注散热器预应力设计的合理性。

不论是否考虑散热器预应力，计算得到的寿命都较实测结果高，经分析认为这是由焊点形状不规则、内部包含空洞缺陷等因素导致的。后续将考虑尺寸偏差和空洞缺陷的影响，并对其影响程度进行修正。

本文研究得到的模型参数和仿真方法可用于后续其他类似产品的焊点寿命预测。