低熔点金属相变热沉热控性能优化研究*
杨小虎,黄崇海,陈 凯,陈 列
(武汉第二船舶设计研究所热能动力技术重点实验室,湖北武汉 430205)
引 言
相变材料是指在一定的温度或温度范围内,通过吸收或释放大量潜热发生固液相变的一类材料。相变材料可以在恒定的温度下实现大容量的热量储存或释放,具有储热密度大、传热㶲损失小、结构紧凑、工作稳定等特点,可有效解决工程实践中热量的供给和使用在时间、空间和量级上的不匹配问题,在太阳能利用、电网削峰填谷、建筑节能和室温调控、冷链物流、航天器热防护、动力电池热管理和光电器件热控等领域得到广泛应用[1],尤其是在电子器件热控领域,基于相变材料的热控技术可应用于周期性发热器件或功率波动器件的温度控制[2-4]。相变热控技术是一种被动式冷却技术,它利用相变材料在熔化过程中吸收大量潜热而温度保持不变的特性来抑制芯片温升,防止其在工作过程中发生过热损坏。当芯片停止工作后,相变材料将吸收的热量释放到周围环境中并凝固,为抵抗下一次热冲击做好准备。
随着各类光电元器件不断向高集成度、小型化发展,其发热功率和发热密度也随之增加,“热障”问题日益凸显。针对长时间高热流密度主动冷却需求,基于液气相变的主动两相对流冷却技术得到迅速发展[5],而针对短时间抗热冲击冷却需求,则适合采用基于相变材料固液相变的被动冷却技术。传统的有机相变材料热导率低(一般在0.1~0.2 W/(m·K)量级),传热能力差,严重阻碍了热量在相变材料内部的传递,从而限制了其热控性能。低熔点金属相变材料固有的高导热特性(热导率在10~40 W/(m·K)量级)赋予了其优异的传热及储热能力,可实现对芯片短时高热量的高效快速吸收,从而有效抑制芯片温升,打破了传统有机相变材料热控性能极限,在应对芯片高功率/高热流热冲击方面展现出明显优势,一经提出便引起了国内外学者和产业界的广泛关注[6-9]。
不同于传导冷却和对流冷却等稳态问题,固液相变冷却过程是具有移动固液边界的复杂非线性瞬态过程,理论分析十分困难。因此目前针对相变热沉的设计和分析往往采用实验和数值模拟的方法[10-11],缺乏快速高效的热控性能分析预测模型,尤其是针对低熔点金属相变热沉,目前对其耦合传热特性和优化设计准则尚不明晰。构建低熔点金属相变热沉热控性能分析模型,对深刻认识低熔点金属相变热控特性和提升相应的热控技术的高效开发和优化设计能力具有重要价值。
本文介绍了金属翅片强化的低熔点金属相变热沉的热控性能快速分析预测模型,利用实验结果对模型的可靠性进行了验证。在此基础上构建了相变热沉优化设计的一般流程,针对任意均匀热冲击边界条件,揭示了热沉关键几何参数对热控性能的影响规律,得到热沉几何参数的优化设计值,并进一步分析了热沉结构材料和相变材料的热物性强化对热沉性能的影响,给出了相应的热控性能预测图表。
1 模型与方法
1.1 热阻模型
固液相变传热问题是具有移动边界的瞬态问题,原则上不能用热阻模型来分析。针对这一问题,文献[12]提出了一种简化方法,即在相变材料完全熔化时的临界时刻构建准稳态热阻模型来估算热沉的热控性能。伴随着热源持续放热,相变材料吸热熔化,形成固相和液相2个区域。相变材料液相区域是热沉底部结构和翅片结构与相变材料固相区域之间的主要传热热阻区域,随着吸热熔化过程的推进,液相区域厚度不断增加,热阻也随之增大。在此过程中,热源温度缓慢上升。相变材料完全熔化后,不再具备潜热储热能力,热源温度将迅速上升。相变材料完全熔化时刻是热源温度变化的拐点,在临界情况下,热冲击结束时相变材料刚好完全熔化,此时热源温度达到最高值Tmax,只要此温度不超过热源容许的最高温度,相变热控方案就可行。因此,获得相变材料完全熔化时的热源温度Tmax是评价和优化热控方案的关键。
图1为相变热沉几何模型及基本分析单元热阻模型。热源热量通过热沉底板和翅片向相变材料传递,相变材料顶部中心位置是距离热沉底板和翅片最远的位置,因此也是最后熔化的位置,建立热沉底部到相变材料顶部中心位置的热阻模型,即可获得相变材料完全熔化时的热源温度。在准稳态近似假设下,热源最高温度Tmax可通过公式(1)热阻网络换热方程计算:

式中:Tm为相变材料的熔点;q和q′′分别为通过热沉基本单元底部的热流量和热流密度;W为基本单元中相变材料的宽度;df为翅片的厚度;B0为热沉总体深度;Rtot为热沉底部到相变材料顶部中心位置的总热阻。
Rtot可用公式(2)表示:

各分热阻项的含义和各几何参数的定义见图1(b)。值得注意的是,这里假定了热沉底部的热流密度分布均匀,且底部各处温度相同,在热沉底板面积与热源面积相差不大且热沉导热性能好时,这是近似成立的。
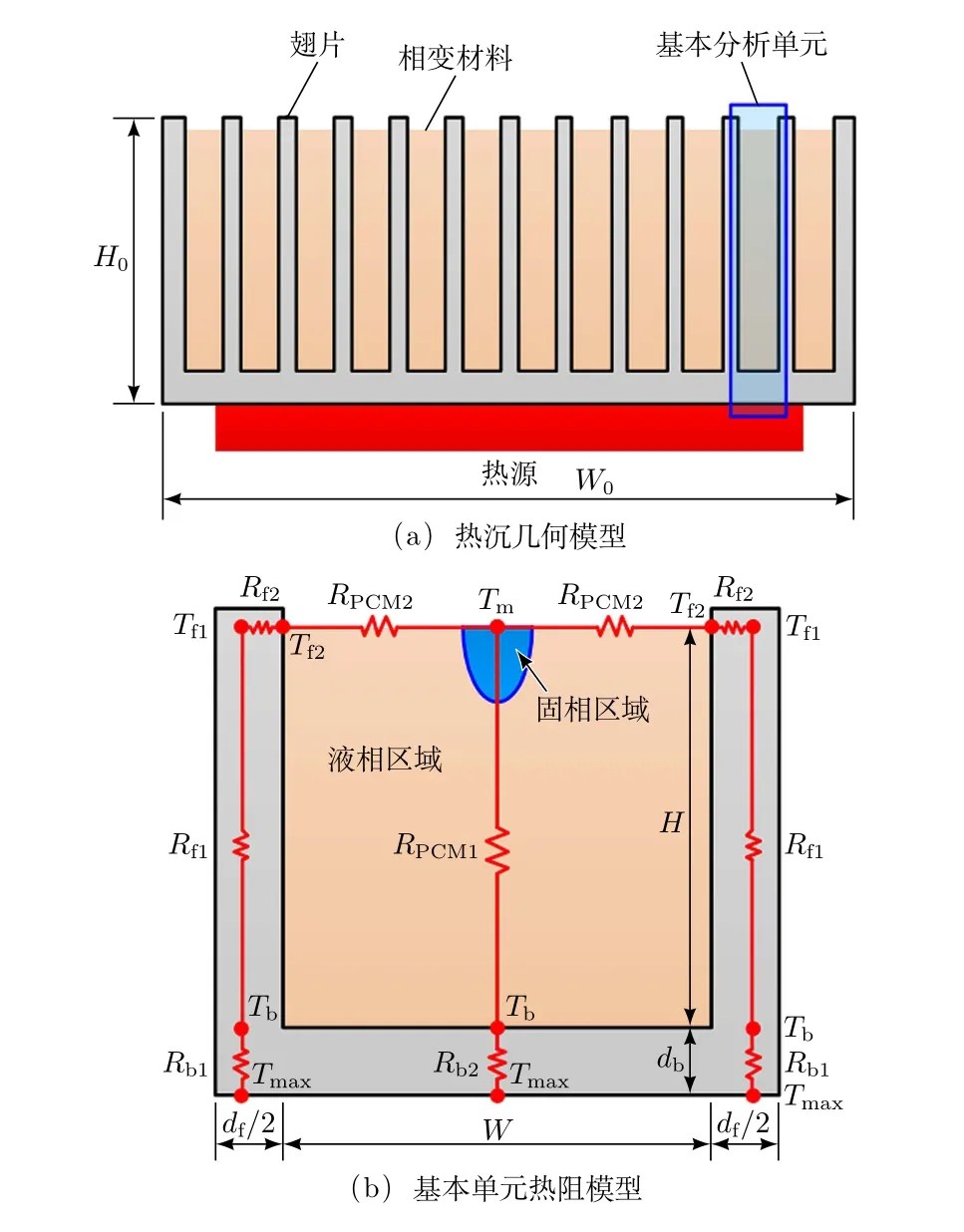
图1 相变热沉示意图
1.2 模型验证
为验证热阻模型的可靠性,将其与之前的实验结果[13]进行了对比,如图2所示。实验测试了3种不同加热功率(80 W,200 W,320 W)下3种不同翅片数的E-BiInSn相变热沉的温度响应曲线,可以根据温度曲线拐点确定相变材料完全熔化时热沉底部的温度Tmax。

图2 热阻模型与实验结果对比
从图2可以看到,热阻模型预测的热沉最高温度值与实验测试结果吻合良好,偏差在±6%以内。同时可以看到,热阻模型预测值普遍高于实验测试值。这主要是因为实验中热沉存在对外自然对流散热,减小了相变材料的吸热功率,而在热阻模型中没有考虑这部分热量损失,因此模型预测的热沉温度会偏高。当然,这部分偏差对热沉的保守设计也是有利的。
1.3 优化设计方法
对于任意给定的热源几何尺寸(Ws×Bs)和热脉冲情况(热脉冲功率Q,热脉冲时间tp),可按图3所示的流程对相变热沉进行设计和优化。
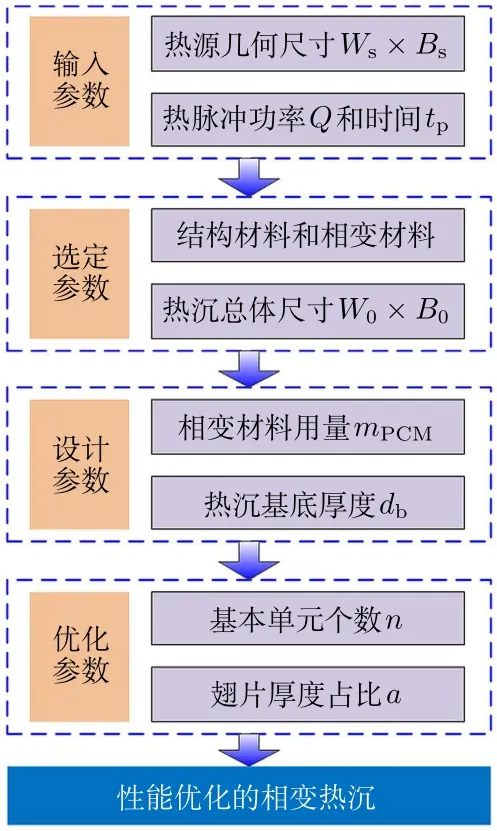
图3 相变热沉优化设计流程
1.3.1 热沉结构材料和总体尺寸
热沉结构材料一般选取热导率较高的金属材料,常用铝质或铜质结构材料。热沉总宽W0和纵深B0适当大于热源尺寸,并认为其热流密度均匀。它们的计算式如下:

式中:K1和K2为扩展系数;Ws为热源宽度;Bs为热源纵深。扩展系数Ki一般在1~2范围内,这里选定为1.5。热沉基底厚度db一般在1~3 mm量级,这里设定为2 mm。
1.3.2 翅片个数和尺寸
利用n −1个翅片将热沉等分为n个基本单元,翅片的厚度与基本单元的宽度之比是一个重要参数,记为α:

式中:W为基本单元中相变材料厚度;df为翅片厚度。它们均可表示为n和α的函数:

1.3.3 相变材料的选择、用量和高度
在相变材料的选择方面,首先要确保相变材料的熔点在合适的范围内,可进一步参考之前给出的相变材料优值系数的概念[14]进行择优选择以获得更好的热控性能。相变材料的用量由所需的储热量决定,可按公式(7)估算:
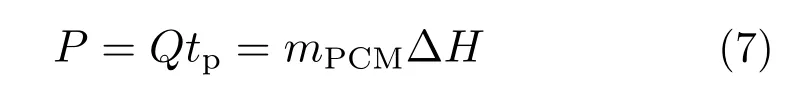
式中:P为芯片在热脉冲时间段内的总发热量;mPCM为相变材料的用量;ΔH为相变潜热值。
基本单元中相变材料的高度H可由公式(8)计算:

式中,ρPCM为相变材料的密度。
1.3.4 热沉结构几何参数优化
一旦选定结构材料和相变材料,相变热沉的性能优化就主要靠改变结构尺寸来实现,主要通过选取不同的n和α来优化热沉性能。利用1.1节中热阻模型的公式可以获得不同n和α下热沉的最高温度Tmax,使Tmax最小的参数组合即为优化的方案。
2 结果与讨论
这里针对尺寸为2 cm× 2 cm、热脉冲功率Q为50 W、热脉冲时间tp为50 s的发热芯片进行相变热控分析。选择典型的低熔点金属铋铟锡共晶合金Bi31.6In48.8Sn19.6(E-BiInSn[13])为相变材料,铝或铜为热沉结构材料,尺寸为3 cm×3 cm,其主要热物性见表1。

表1 热沉结构材料和相变材料主要热物性
2.1 E-BiInSn/铝热沉性能
图4给出了翅片个数n和翅片厚度占比α对EBiInSn/铝热沉最高温度Tmax的影响。基本单元个数越多(即翅片数越多),热沉最高温度就越低,且当基本单元个数达到5以后,继续增加翅片数对热沉性能的改善已无明显作用。热沉最高温度随翅片厚度占比的增大呈现先降低后升高的趋势,说明存在最优的翅片厚度选择。翅片太薄会影响翅片自身的纵向热传导,而翅片太厚则会导致相变材料区域变窄,同样不利于热量在相变材料内部的传递。对于给定的热控需求(50 W,50 s),当基本单元个数为4或5,翅片厚度占比为0.5时,即可达到最优的热控效果,此时相变热沉底部的最高温度为74.5°C,在芯片允许的温度范围内。

图4 翅片个数n和翅片厚度占比α对热沉最高温度的影响
2.2 E-BiInSn/铜热沉性能
图5对比了铜质结构材料和铝质结构材料对热沉性能的影响。各设计参数对应的热沉最高温度Tmax的具体数值已在图中标注(对应图右侧栏)。

图5 结构材料对热沉性能的影响
对于E-BiInSn/铜热沉(图5(b)),当基本单元个数n为5或6,翅片厚度占比α为0.5时,即可达到很好的热控效果,此时相变热沉底部的最高温度达到最优,为67.8°C。相比而言,铝质结构材料热沉的最高温度的优化值为74.5°C,两者相差6.7°C。由于铜材重量重,价格高,因此实际使用时在满足热控性能的前提下,优先使用铝作为结构材料。在后面的研究中,如无特别说明,默认结构材料为铝。
2.3 相变材料热物性改进
相变材料热导率对相变热沉热控性能有着重要影响。图6展示了在前述优化几何尺寸下(n= 5,α= 0.5),相变材料的热导率对热沉性能的影响。不难理解,相变材料的热导率越高,热源最高温度就越低。当相变材料的热导率低于5 W/(m·K)时,热沉的热控性能随热导率的降低迅速恶化,最高温度急剧上升。当相变材料的热导率高于10 W/(m·K)后,增加热导率带来的热控性能改善并不明显。因此,对于石蜡类低热导率(0.1~0.3 W/(m·K)量级)相变材料,提高热导率是十分必要的,而对于低熔点金属相变材料(热导率一般在10~35 W/(m·K)量级),对热导率的提升需求并不大。而且,为提升热导率而采取的强化措施(如添加纳米颗粒、采用泡沫金属等)反而会使其单位体积内的相变潜热降低,影响其储热能力。

图6 相变材料热导率对热沉性能的影响
对于E-BiInSn,可使用泡沫金属铝来增强其导热性能,形成E-BiInSn/泡沫铝复合相变材料。复合材料的等效热导率λeff可用Bhattacharya模型[15]计算:
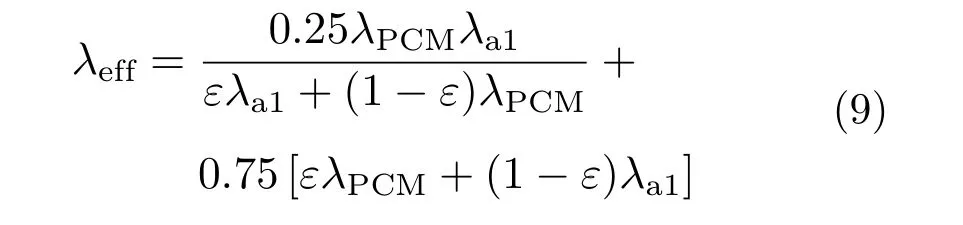
式中:ε为泡沫铝的孔隙率;λa1为铝的热导率;λPCM为相变材料的热导率。
由于泡沫金属占据部分体积,同等体积下相变材料的量变少,因此在前述热阻模型中,计算相变材料的高度时(式(8)),需要将ε考虑进去,得:

不同孔隙率下E-BiInSn/泡沫铝复合相变热沉(铝质结构材料)的热控性能见表2。

表2 不同孔隙率下E-BiInSn/泡沫铝复合相变热沉(铝质结构材料)的热控性能
图7展示了不同孔隙率下E-BiInSn/泡沫铝复合相变热沉在不同单元数和不同翅片厚度占比下的热控性能对比。从图7可以看出,尽管在添加泡沫铝后,相变材料的等效热导率显著增加,有助于提升其热控性能,但由此造成的单位体积内有效潜热的减小反过来又会影响其热控能力。通过对比分析可以发现,在不同孔隙率下,E-BiInSn/泡沫铝复合相变热沉最优的热控温度并没有降低,反而有小幅增加,也就是说热控性能有所下降。

图7 不同孔隙率下E-BiInSn/泡沫铝热沉(铝质结构材料)的热控性能对比
泡沫金属孔隙率越小,代表金属占比越大,相应的最优翅片厚度占比就越小。这是因为泡沫金属与金属翅片实际上扮演的是相同的角色,两者可互相取代。显然,使用金属翅片更加方便,成本更低。因此,对E-BiInSn相变热沉而言,使用泡沫金属提升等效热导率是没有必要的,仅需使用简单的金属板翅结构即可达到很好的传热增强效果。
3 结束语
本文利用相变材料完全熔化临界时刻的准稳态热阻模型给出了相变热沉优化设计的一般方法,重点对均匀热流密度边界条件下低熔点金属相变热沉进行了分析和优化设计。金属翅片的引入可有效增强低熔点金属相变热沉的热控性能,翅片个数和翅片厚度占比是影响热沉性能的关键几何参数。翅片个数的增加可增强热沉的热控性能,但增加到一定个数后会趋于极限。翅片厚度存在最优的选择,过厚或过薄都会对热沉性能产生不利影响。低熔点金属相变材料固有的高导热特性使其对热导率的提升需求并不大,采用泡沫金属或添加纳米颗粒等传统有机相变材料常用的强化传热措施对低熔点金属并不适用,反而会使其单位体积内的相变潜热值降低,影响热控性能,而使用简单的金属翅片结构强化传热即可实现很好的热控性能改善效果。

