三维电场覆冰绝缘子PD等离子体仿真研究

冯宇宁，蔡志远，苑经纬，胡大伟，葛建宁

(1.沈阳工业大学特种电机与高压电器重点实验室，辽宁 沈阳 110870；2.国网辽宁省电力有限公司，辽宁 沈阳 110006；3.国网辽宁省电力有限公司电力科学研究院，辽宁 沈阳 110006；4.河北硅谷化工有限公司，河北 邯郸 056000)

我国地域辽阔，气候多样，东北某重工业城市冬季严寒，输电线路绝缘子易发生覆冰的情况。供暖及工业生产均会对大气造成一定程度污染，大气污染导致覆冰绝缘子的水电导率增加，覆冰绝缘子在融冰期易发生闪络事故，严重威胁电网安全运行[1]。对覆冰绝缘子闪络机理进行研究，需要在多学科多领域开展，较为复杂，试验条件苛刻，数学模型建立难度大。国外学者对绝缘子污闪与冰闪进行了大量系统性研究，并建立了用于预测闪络电压的宏观数学模型。我国在此领域虽然起步较晚，但在专家学者努力下，也取得了很多较有价值的成果。重庆大学蒋兴良对覆冰绝缘子进行了包括完善预测闪络电压的数学模型[2]及电场分析[3]等大量研究；沈阳工业大学陈刚和苑舜等人应用有限体积法对液滴进行流体场计算，根据覆冰绝缘子机理，研发了一种利用电热去冰来防止绝缘子覆冰的半导体憎水性涂料；同时研发了一种全新的组合式室温硫化硅橡胶长效防污闪(RTV)涂覆方法，应用该涂覆方法可在几乎不提升绝缘子正常工作状态时能耗率的前提下，在其覆冰状态下产生足够的热量来阻止冰层形成[4]。这些成果能够为电网防冰闪工作提供有效的理论和实践支持。以往人们对冰闪研究集中在用试验来对其闪络过程中的表面现象进行总结，利用仿真对其稳态的电场分布进行研究与优化。虽然绝缘子电场分布可以在一定程度上反映绝缘子的状态，但在局部放电及闪络发生后，其电场分布情况发生改变，此前专家学者通过构建动态的数学模型对其放电和击穿本质的研究较少。本文提出导致气隙击穿的原因为强场区产生足够的高密度带电粒子，在电场影响下定向运动，直至形成贯穿气隙的导电通道的假设。以金具与近金具冰棱下端的最短距离为击穿路径，结合国内外学者对覆冰绝缘子的研究，考虑了带水膜冰层的三维结构，通过三维电场有限元仿真，确定了气隙击穿路径的电场分布情况。将电场分布情况带入等离子体模型，模拟气隙击穿过程中击穿路径上的等离子体分布情况。通过仿真模型，对提出的假设进行研究与验证。

1 基于绝缘子覆冰机理的三维电场仿真

1.1 仿真模型建立的理论基础

对覆冰绝缘子研究一直是具有挑战性的课题，其主要原因如下。

a.冰体结构难以确定，冰体不同区域导电性不同，在绝缘子带电情况下形成的冰体与不带电情况下形成的冰体不相同，难以对带电情况下形成的冰体进行测量。

b.从覆冰到闪络的故障过程时间长。

c.设计闪络与局部放电的理论跨越多个学科，涉及到等离子物理等前沿领域。

本文针对中重度覆冰绝缘子进行研究，此状态下的绝缘子通常在迎风侧形成一定厚度的冰层，根据绝缘子布置方式，气隙可能存在于下金具与下伞裙之间，气隙间通常存在一定长度的冰棱[5]，冰层本身电导率较低。闪络事故大多发生于融冰期，此时冰体表面存在0.015 mm厚的水膜，该水膜电导率较高[6]，在局部放电发生前，大部分电压集中在气隙两端[7]，此刻绝缘子的电场分布可用稳态静电场描述。

考虑冰棱对电场分布的影响，使用三维模型进行静电场仿真，空间电场梯度通过泊松方程进行求解。

式中：φ为电位，V；ε为介质的相对介电常数；ρ为空间电荷密度，C/m3。仿真模型如图1所示。

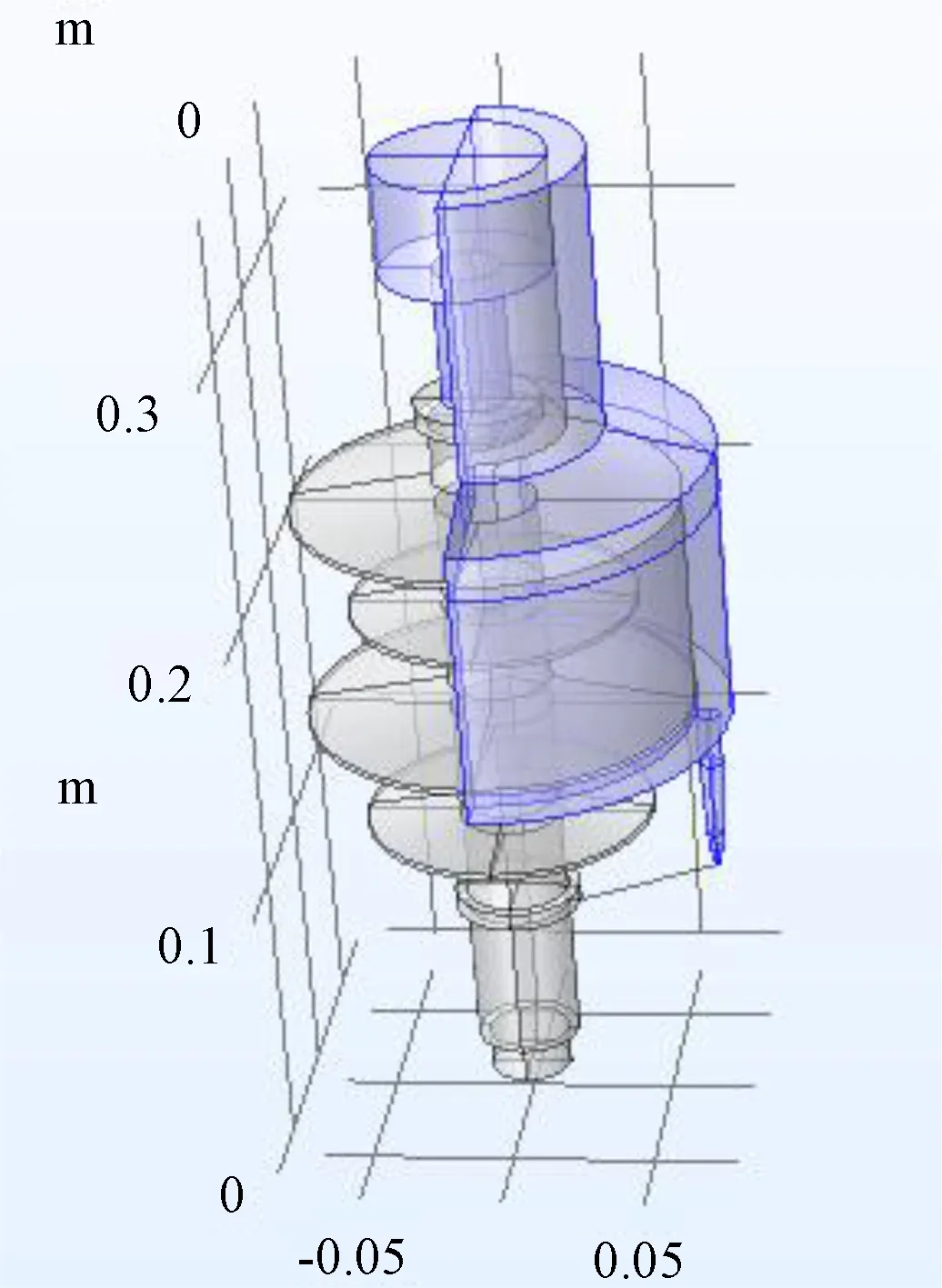
图1 仿真结构

1.2 三维稳态静电场仿真分析

在模拟稳态电场的过程中，由于冰层表面水膜具有一定的导电性，且上端与上金具直接接触，气隙未击穿，气隙两端电阻无穷大，因此几乎全部电压集中在气隙处。此模型设置下金具为接地端，上金具为高压端，冰体表面与上金具电位相同。为确保气隙击穿现象产生，高压端设置电压-72 kV，远大于该类型绝缘子额定电压。三维电场分布切面如图2所示。

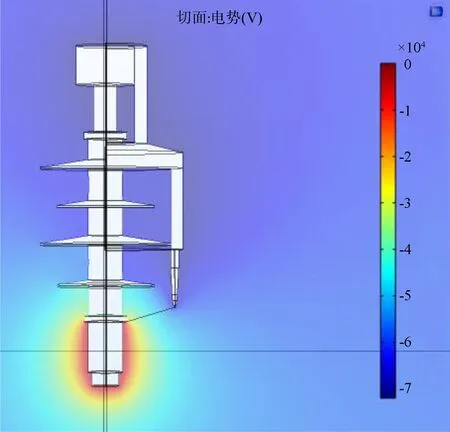
图2 三维电场分布切面

在局部放电和闪络发生后，绝缘子电场分布发生改变，覆冰绝缘子最初的气隙击穿发生于电场强度最大，并且能够贯穿气隙的距离最短区域。因此假设气隙击穿发生于金具与冰棱相连的最短路径上(图2中红线)，此路径上的电场分布极为重要。

图3为击穿路径的电场强度分布，距离0 m处为靠近金具的位置，右侧末端为靠近冰棱的位置。由图3得出以下结论。

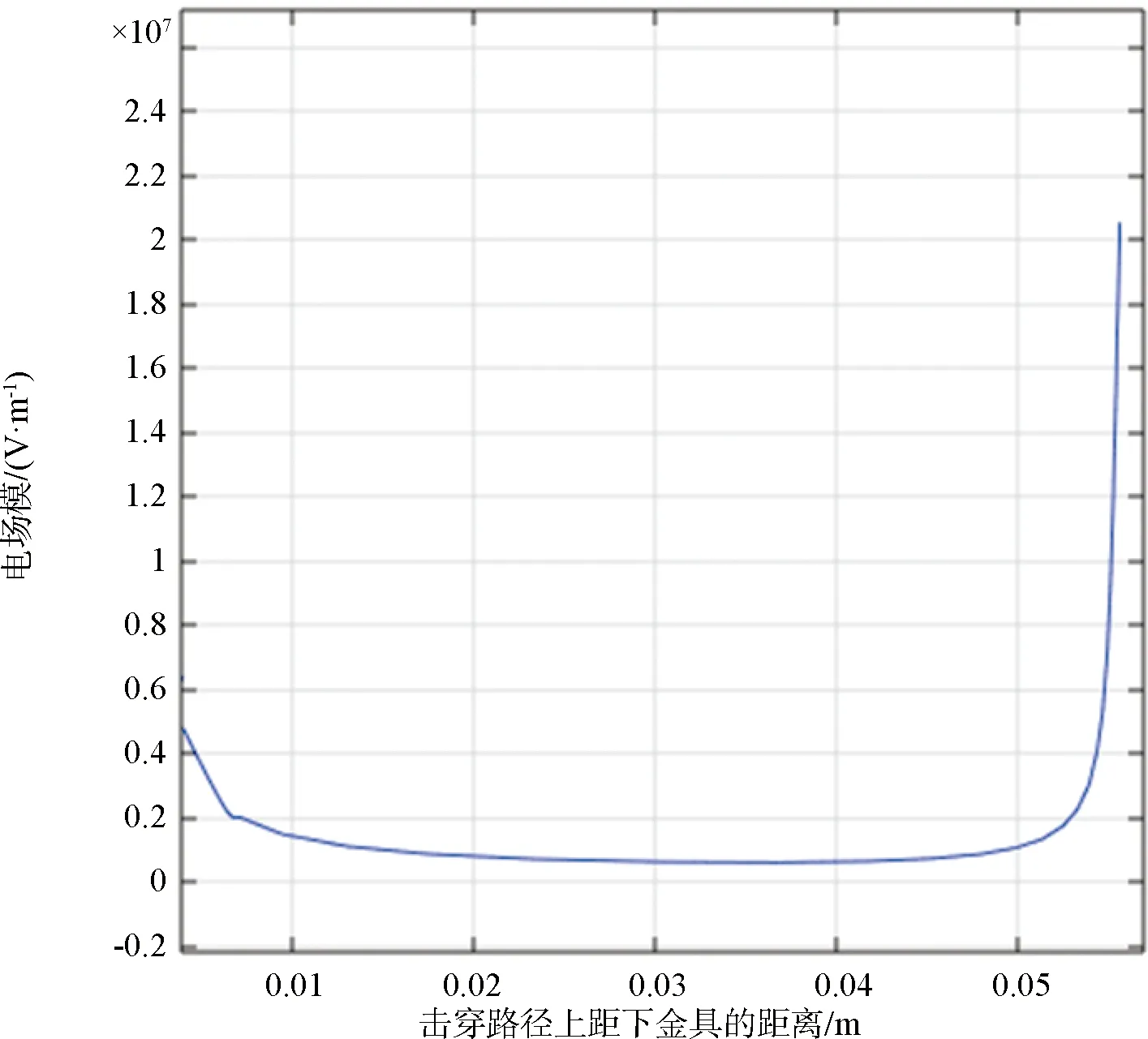
图3 击穿路径上的电场强度分布

a.击穿路径上的电场强度为两端高中间低，两端的电场强度呈指数变化趋势。靠近冰棱处的电场强度增加速度明显超过靠近金具处的电场强度增加速度。在击穿路径中间的大部分区域内，电场强度较低。

b.冰棱周围电场强度变化剧烈，局部电场强度已经超过空气击穿电场强度3×106V/m，在此状况下局部放电的发生难以避免。

c.绝缘子表面任何与高压端或接地端导通的尖锐突起的导电结构会严重畸化附近的电场分布，导致局部电场强度增加。由于高压端与接地端附近电场强度呈指数增加趋势，因此缺陷导致的电场畸变效应会大大增强，易导致局部放电的发生。

2 三维电场等离子体电击穿仿真

2.1 仿真原理

在未靠近电极与冰棱的大部分区域中，电场强度分布均匀，约为-6.65 kV/cm，该值较低，低于空气击穿场强。大量试验表明，该结构的绝缘子在覆冰水电导率足够高的情况下，两端承受-72 kV的电压时会发生闪络事故，因此可判断气隙击穿会在闪络事故前发生。本文根据等离子体理论及高电压工程理论，对气隙击穿的原因进行分析，并且通过对电子崩头部在不同初始带电粒子浓度时，电子崩发展的瞬态特性进行仿真并验证。

在带电粒子受电场力移动过程中，逃逸带电粒子的能量主要由电场力提供，其所受阻碍主要为碰撞损失的能量。在足够高的电场强度下，带电粒子在2次碰撞之间获得的能量，将大于碰撞损失的能量，此时自由带电粒子进入持续加速状态；若带电粒子在2次碰撞之间获得的能量小于碰撞损失的能量。此时带电粒子能量逐渐降低，路径中的带电粒子数逐渐减少[8]。

根据高电压工程相关理论，此情况类似“极不均匀电场”中的气体击穿过程，强场区的带电粒子大量电离，出现带电粒子累积，曲率半径较小的电极表面开始出现放电现象，形成电子崩，并不断向另一极发展[9]。

通过建立介质阻挡放电(DBD)模型，模拟气隙间的电击穿过程，因为场强较高，判断放电类型是以迁移为主的电子和离子通量类放电。因等离子体仿真计算及其复杂，为保证计算成功，在求解过程中采用Comsol软件等离子模块中特有的有限体积离散化处理。具体计算方程如下。

进行静电场求解，通过泊松方程，计算等离子体的电势，通过电子和其他带电粒子的密度计算空间电荷密度。

-▽·ε0εr▽V=ρ

(2)

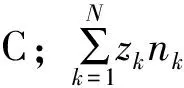
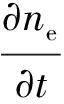
(4)

式中：Γe为电子通量，1/(m2·s)；u为质量品平均速度，m/s；Re为电子速率。

式中：xj为反应j的目标物质的摩尔分数；αj为反应j的汤森系数,m2；Nn为总中性数密度，1/m3。

模型采用“局部场近似”进行求解，无需求解电子能量密度方程，传输系数和源系数通过约化电场来映射。各种重物质的质量分数为

式中：ρ为气体密度，kg/m3；wk为质量分数；Rk为速率，kg/(m3·s)；jk为扩散通量向量，kg/(m2·s)。

模拟常压下气体的电击穿，计算过程非常复杂。为了使计算成功，揭示气隙击穿过程中的现象，对空气的化学反应进行一定简化，适当减少了物质和反应数量。由于空气中的氮气体积分数为78%，因此采用氮气的化学反应替代空气进行计算。氮中等离子体的化学性质非常复杂，若对主要激发态进行详细研究，有数百种反应需要考虑，因此模型还需根据研究目标对计算的电离反应情况做一定简化。本文主要是研究强电场下的带电粒子密度分布，因此在计算过程中，只使用如表1所示的电离反应，如表2所示的表面反应。

表1 电离反应

表2 表面反应

一直以来，专家学者对绝缘子局部放电至闪络过程中局部电弧进行了一系列研究，这些研究绝大多数以试验为主。经研究发现，该阶段产生的局部电弧具有以下特征：①局部电弧发展的初始阶段，泄漏电流较小，一般在0.01～0.1mA；②局部电弧半径为

式中：参数k由Farzaneh等人研究确定，与高压端极性有关，高压端为正极性时与高压端为负极性时所对应的k值分别为1.75与1.67。

设定高压端电势值为负，k值取1.67，根据式(2)可推算局部电弧半径在1.38～4.4 mm。气隙击穿前的等离子体流柱产生于局部放电之前，可推断其半径更小，并且气隙击穿所经历的放电反应时间极小，因此只考虑击穿路径中的径向等离子体分布，采用一维模型进行仿真。

假设因两端场强较大而造成的空间带电粒子的积累，对气隙击穿的进程具有决定性作用。由于气隙击穿路径一侧与下金具相连，另一侧与冰棱下端相连，虽然覆冰绝缘子冰棱周围电场强度更高，但因其与金具之间的接触方式为金属接触，电荷更易导出，因此假设局部放电先发生在靠近金具表面的空气中。由于等离子体仿真计算量极大，冰棱下端距下金具的距离过大，因此对击穿路径的全部区域进行仿真不现实。为实现研究目标，截取击穿路径中间的一小段区域，模拟电子崩在场强相对较低区域的发展状态，截取从电子崩头部到冰棱下端路径上的一小段距离，模拟电击穿过程的瞬态特性。专家学者对放电现象进行过大量研究，认为随着电子崩发展，电子崩头部存在一定密度的自由电子。由于仿真模型的最左侧为电子崩头部，因此通过改变此处的电子密度，模拟电子崩头部电子密度对气隙击穿进程的影响。根据三维电场仿真结果，在击穿路径上设置-6.65 kV/cm的恒定场强。

2.2 DBD仿真分析

假设电子崩头部最大电子密度为1.4×1024m-3。击穿过程中，带电粒子密度随时间的变化趋势如图4所示，电场强度随时间的变化趋势如图5所示。图4中实线为电子密度，虚线为带电离子密度。

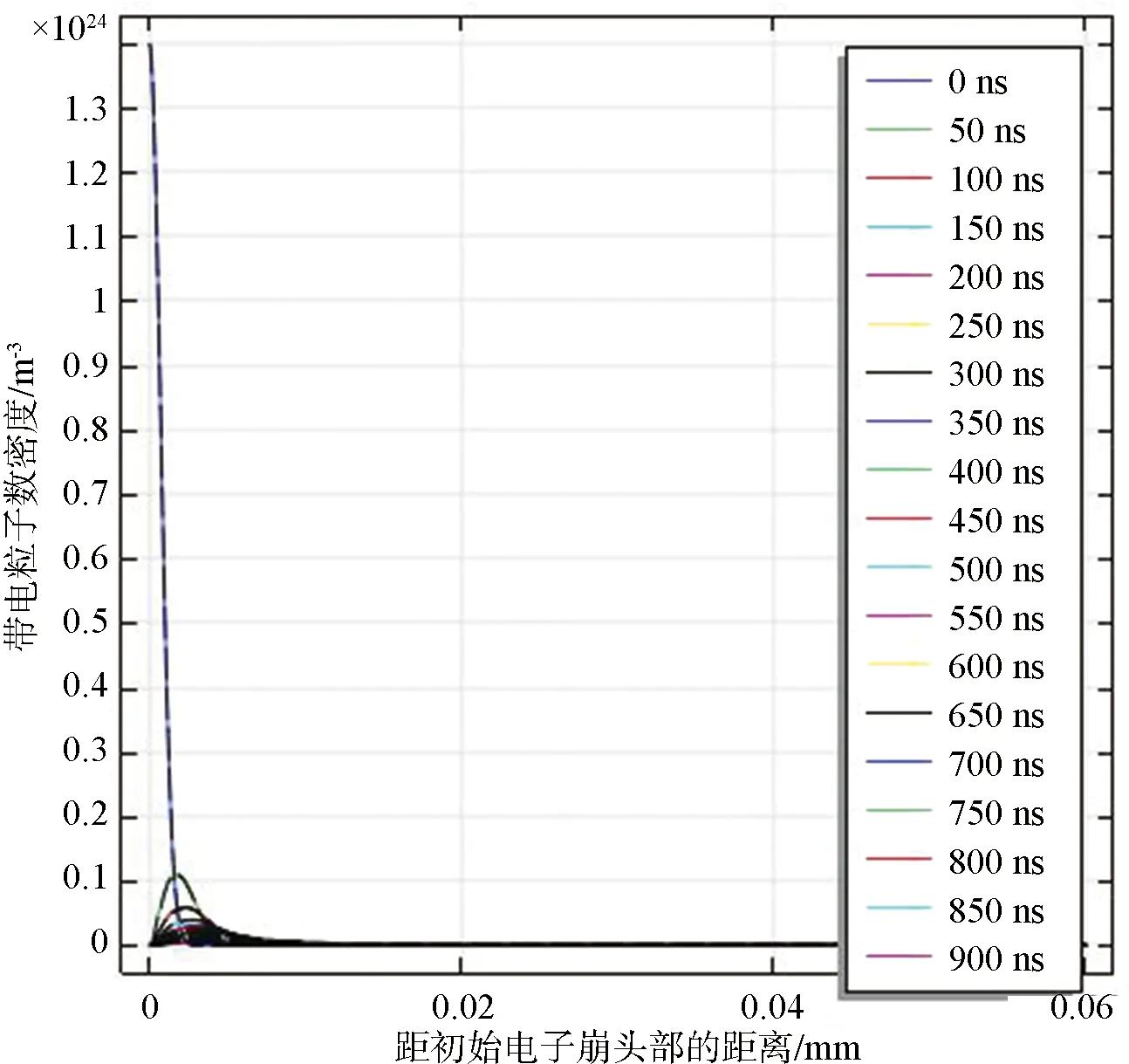
图4 初始电子密度1.4×1024 m-3时带电粒子密度随时间的变化趋势

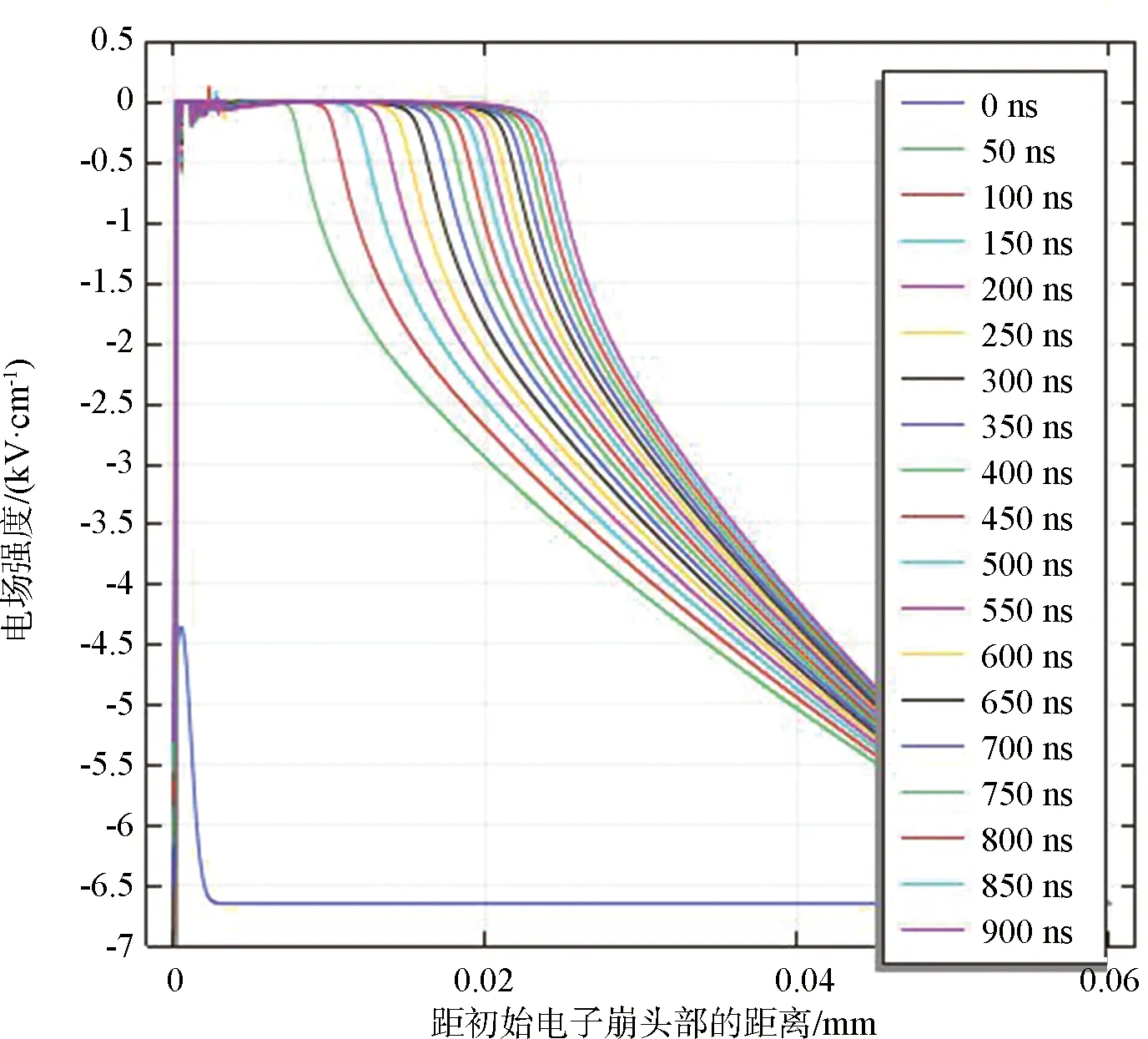
图5 初始电子密度1.4×1024 m-3时电场强度随时间的变化趋势

由图4可以看出，在-6.65 kV/cm恒定场强下，因碰撞造成的能量损失导致击穿路径上的带电粒子密度呈指数趋势下降。

由图5可判断，电场强度为零的区域已经发生了电击穿。虽然在-6.65 kV/cm恒定场强下，能量损失会导致击穿路径上的带电粒子密度迅速下降，但并未影响电击穿路径发展。

假设电子崩头部最大电子密度为1.4×1021m-3，带电粒子密度随时间的变化趋势如图6所示，电场强度随时间的变化趋势如图7所示。

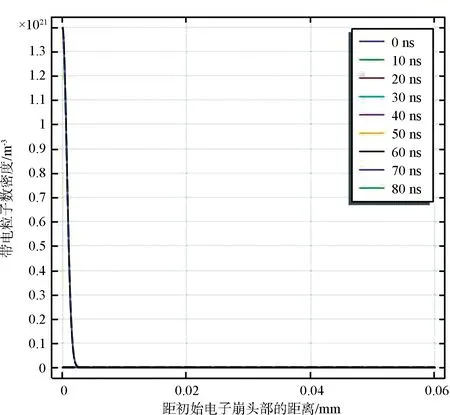
图6 初始电子密度1.4×1021 m-3时带电粒子密度随时间的变化趋势

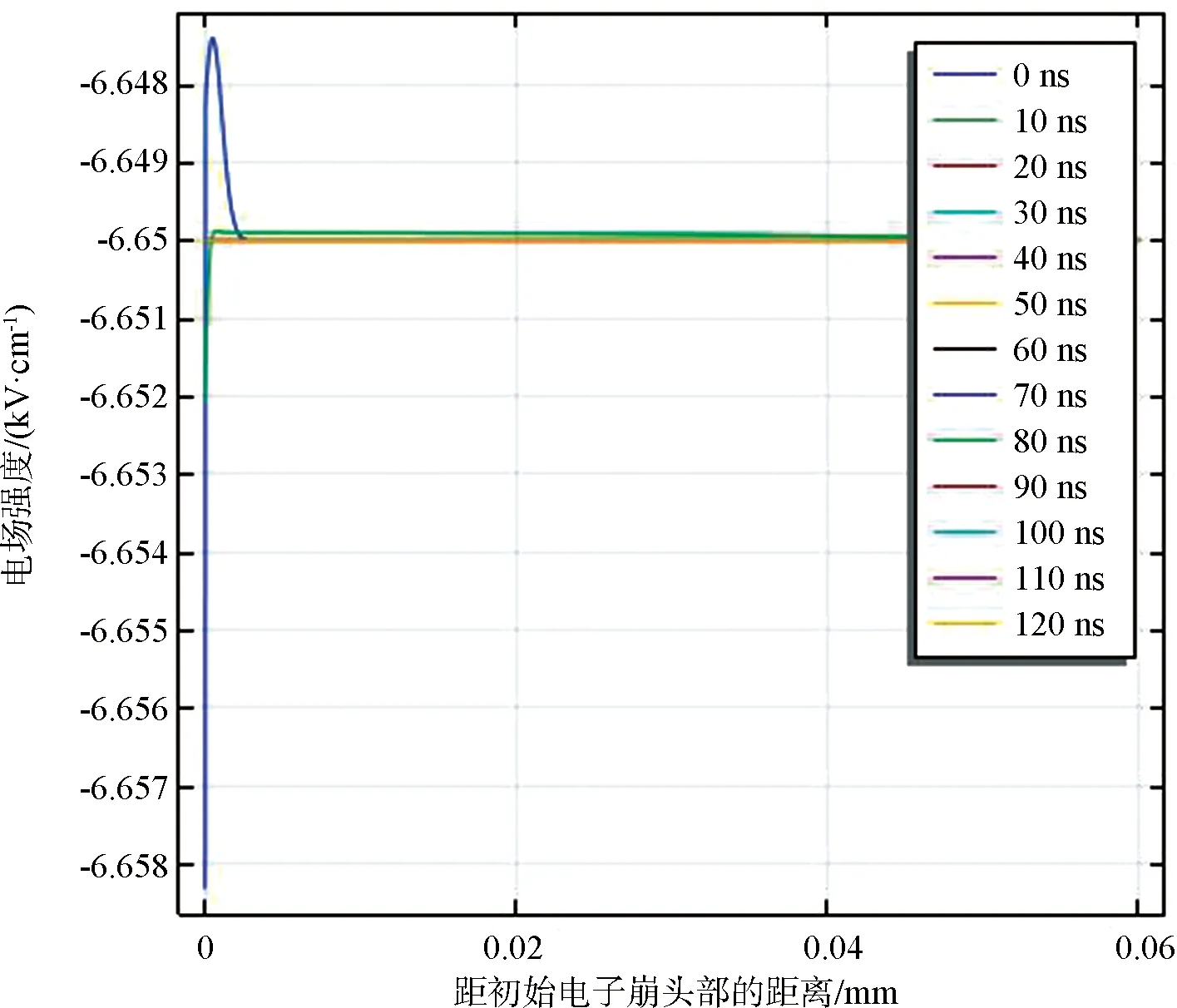
图7 初始电子密度1.4×1021 m-3时电场强度随时间的变化趋势

由图7可知，击穿路径上电场强度几乎保持初始值不变，因此可判断在-6.65 kV/cm恒定场强下，气隙未被击穿。

3 结论

a.在电场强度较小，带电粒子逃逸过程中，当电场提供的能量小于其碰撞损失的能量时，气隙能否击穿取决于气隙中的电子密度。

b.通过对DBD仿真结果进行分析，绝缘子发生局部放电(PD)的原因是由于缺陷处强电场导致带电粒子的产生和累积。