基于向量优化的硬件木马检测技术研究
傅子晗,吴新春,朱书霖,魏红梅
(1. 西南交通大学信息科学与技术学院, 四川 成都 61 1756; 2. 宁波汉达信息科技有限公司, 浙江 宁波 315048)
0 引言
由于集成电路芯片的设计与制造过程非常复杂,每一个步骤都不是完全安全的,硬件木马可能被植入,能够监控或改变原始电路的功能,严重影响了集成电路芯片的安全。我国集成电路行业起步较晚,大多数集成电路需要进口,而不能百分百保证芯片没有硬件木马,因此,有必要对硬件木马检测进行研究。
硬件木马检测领域主要集中在基于反向剖析的检测方法、基于旁路信号分析的检测方法、基于逻辑测试的检测方法等。Potkonjac等人提出了采用基于线性规划和奇异值分解的门级特征公式来检测木马[1],并对延迟和静态功耗进行测量,通过约束方程分析进行木马检测。Nasr. A等人提出了一种高效的面向梯度的逆向工程硬件木马检测方法[2],提出了物理检测三步实现自动化的底层电路版图识别方法。Chakraborty R S等人提出了MERO硬件木马向量优化检测方法[3],它是一种基于内部节点稀有逻辑条件多重激励的测试模式生成技术。Voyiatzis等人提出了基于组合测试的硬件木马检测方法[4-5],其重点放在触发硬件木马的效率上。Hong Zhao等人提出了一种基于信息熵聚类的硬件木马检测方法,采用启发式测试模式生成方法,利用互信息来增加硬件木马逻辑的转换。在电路基准上的实验验证了硬件木马检测的有效性[6]。Chen Don g等人提出了一种结合主成分分析(PCA)和局部离群因子(LOF)算法的无监督硬件木马检测方法PL-HTD[7]。
国内在硬件木马领域的研究起步就比较晚,直到2010年,与硬件木马有关的论文才发表[8]。徐力等人提出一种在电路设计过程中插入二选一数据选择器,从而提高电路节点翻转概率的方法。将电路功耗作为旁路信号,利用旁路信号分析方法进行硬件木马检测[9]。骆扬等人提出了一种具有可操作性的检测物理型硬件木马的方法[10]。冯秋丽等人提出了一种基于节点活性的硬件木马检测方法,以AES为目标电路并植入硬件木马,进行仿真及FPGA实验[11]。刘志强等人提出了一种深度学习的非电信号硬件木马检测算法[12]。李鑫等人提出了一种基于电路结构分析的集成模型,将复杂繁琐的电路图转化为向量数据格式,通过极限梯度提升树和长短期记忆神经网络的集成模型来检测硬件木马[13]。
1 基于稀有节点的硬件木马检测方法
基于逻辑测试检测方法是一种重要的硬件木马检测方法,其核心思想就是激活硬件木马。由于芯片规模不断增大,其输入输出端口数也不断增多,增加了逻辑测试的难度。为了解决此问题,可采用侵入式或非侵入式逻辑测试方法。侵入式逻辑测试是在原始电路加入额外电路方便测试,更容易控制内部触发器,使硬件木马被激活的概率增加,减少硬件木马被植入的风险。非侵入式逻辑测试是基于自动测试向量生成技术来生成大量的测试向量,并对其进行优化,然后选择优化后的向量集来测试电路。而稀有节点是电路中翻转概率低于阈值θ的节点,不同的电路需要选择不同的阈值。基于稀有节点的检测方法的目的就是通过提前分析电路信息,找出电路中的稀有节点,以更高的激活稀有节点转换概率为目标进行对测试向量进行优化,减小测试向量容量。
基于稀有节点的硬件木马检测方法如图 1所示。该方法包括了三个部分,稀有节点查找、向量优化以及木马检测。稀有节点查找时,如果选择较小的阈值θ(θ≦0.25),选择到的节点数量太少,会遗漏一些木马植入节点,如果选择较大的阈值θ,选择到的节点数量太多,效果不好。为了能让设置的阈值θ效果较好,阈值θ设置在能区分30%左右节点较为合适。另外,需要剔除掉错误节点,即翻转概率为0的节点,如GND和VDD。木马检测采用逻辑测试激活硬件木马,从而判断电路中是否存在硬件木马。向量优化将在下节详细介绍。
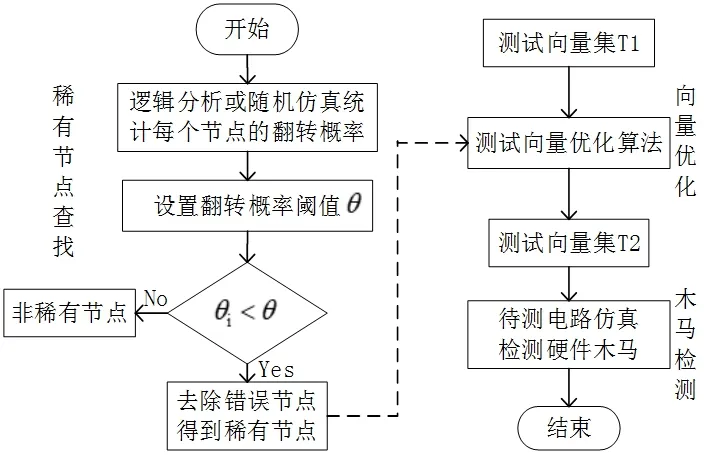
图1 基于稀有节点的硬件木马检测方法Fig. 1 hardware Trojan horse detection method based on rare nodes
2 向量优化算法
测试向量生成主要依靠自动测试向量生成技术,采用优化算法将随机产生的测试向量集 T1转换成效率更高的测试向量集T2,如图1所示。测试向量直接作用是将稀有节点逻辑值改变,向量优化的目标是将硬件木马激活。
记稀有节点 ni被激活的概率为 p0/1(ni),p0/1(ni)代表ni节点为0或者1的概率,其中
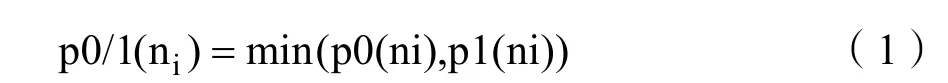
例如 p0(n1)=0.25,p1(n1)=0.75,则 p0/1(n1)=0.25。把向量集T2中的向量条数记为T,采用向量集T2,稀有节点ni被激活的次数Ni定义为:

如图 2所示,稀有节点 n0的激活概率为 p0(n0),稀有节点 n1的激活概率为 p0(n1),稀有节点n2的激活概率为p1(n2),稀有节点n3的激活概率为 p1(n3)。在 np为逻辑 1的情况下,负载逻辑被激活。则np为1的概率即为硬件木马被激活的概率,将木马激活概率P记为:
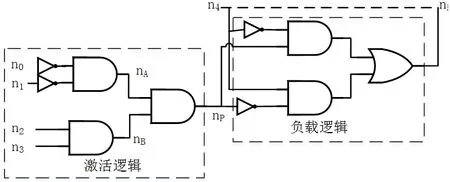
图2 硬件木马激活逻辑Fig. 2 hardware Trojan activation logic

由公式(3)推导,在由n个节点作为硬件木马触发逻辑的输入节点时,并且激活逻辑全由与门组成,则硬件木马激活概率为:

由n个节点作为硬件木马触发逻辑的输入节点,节点之间的激活逻辑全由或门组成时,硬件木马的激活概率为:

从逻辑门的分析可以得出,当激活逻辑全为与门时,硬件木马的激活概率最小;当激活逻辑全由或门时,硬件木马的激活概率最大,即:
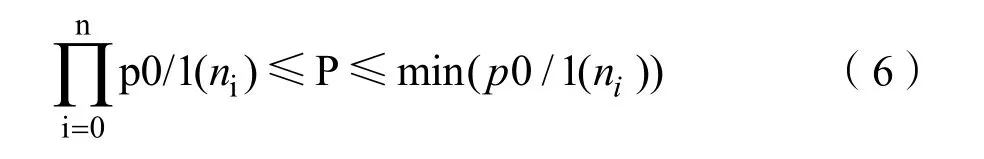
硬件木马的激活次数S为:

引入变量 ns,表示在所有的稀有节点中激活次数最少的稀有节点,即ns稀有节点的激活概率最小

稀有节点数目确定时,p0/1(ni)也为确定值,Ni与向量集 T2中的向量数T成正比,Ns也与T成正比,由公式(2)和(7)可推导出 S和 Ns的关系,
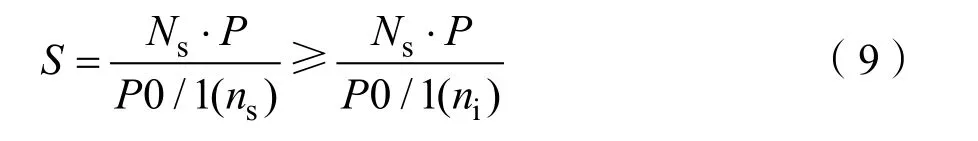
如果硬件木马被激活,S大于等于1即可,则:

通过式(10),优化算法有了新的优化目标,从随机向量集T1出发,算法需要将每条向量进行修改,保证最后的向量集T2能够让每个稀有节点的激活次数至少达到Ns。
通过对优化目标的重新选择,从而设计出基于稀有节点的测试向量优化算法,如图3所示。优化算法需要输入的信息包括稀有节点数目,稀有节点对应的01概率,随机向量集T1,并且需要优化的目标即稀有节点的最少激活次数Ns,以及优化后向量集的向量数目 T,最重要的是需要知道待测电路的逻辑结构。有了这些输入信息后,首先将优化向量集T2清零,各稀有节点已激活次数清零,然后从随机向量集T1中读取每条向量,将每条向量施加于待测电路,统计各条向量下有多少稀有节点被激活,以及向量集激活稀有节点的次数。将向量依据激活的节点个数从少到多排序。选择T条激活稀有节点个数最多的向量,作为需要优化的向量。然后选择激活稀有节点最少的向量开始修改,修改向量的第一位。修改后的向量再次施加于待测电路,判断该条向量激活的稀有节点数是否增加,如没有增加意味着稀有节点的激活次数不达标,拒绝此次修改,如果该条向量激活的稀有节点数增加,再判断各稀有节点的激活次数是否达到最少激活次数Ns,如果达到,则优化过程完成。如没达到,接受该位修改,继续修改下一位,直到改完该条向量。修改完一条向量之后,重新将向量依据激活的节点个数从少到多排序,再从激活稀有节点最少的向量开始修改,直到满足最少激活次数Ns的目标。经过优化算法能够得出最终优化的向量集T2。
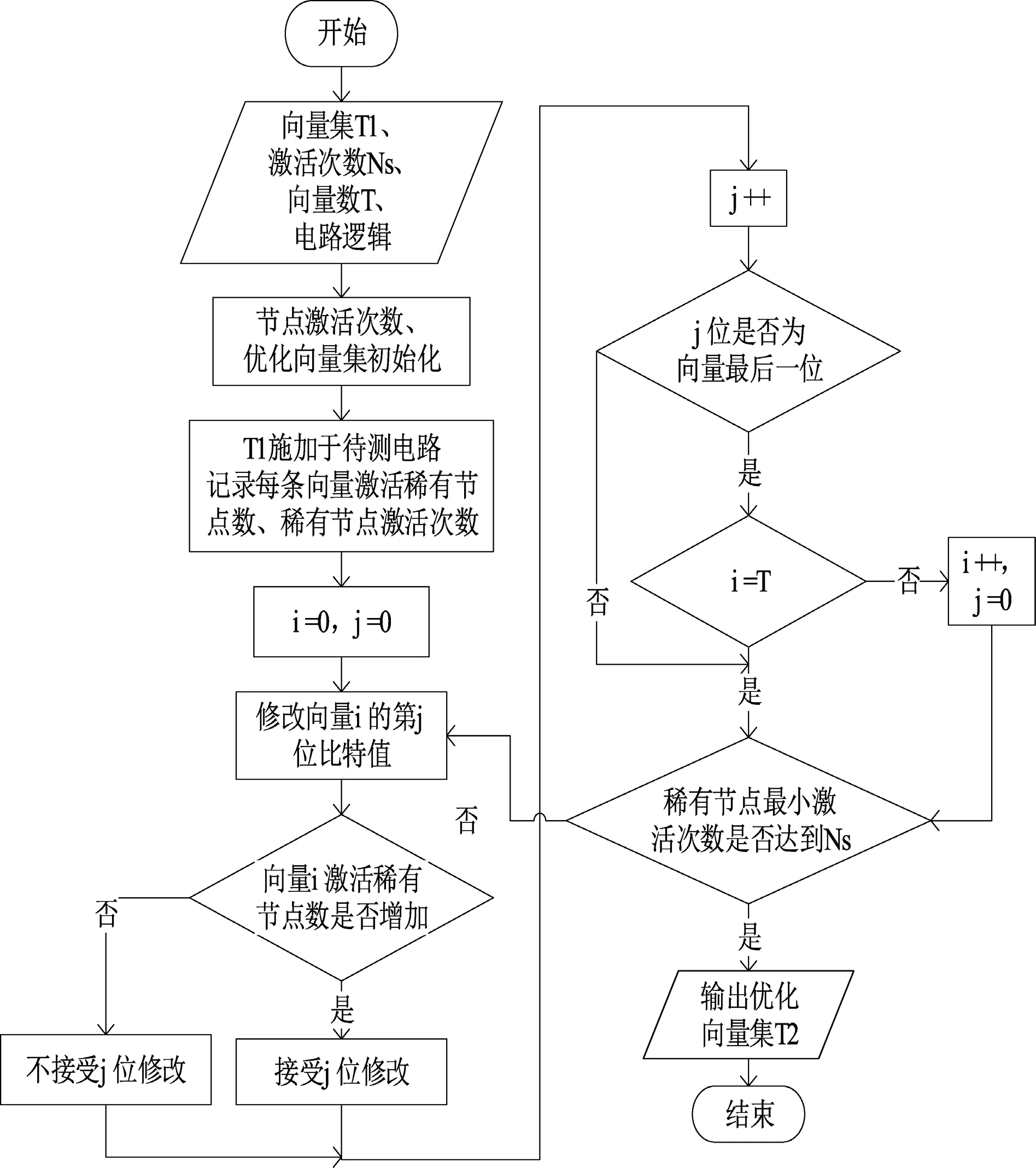
图3 稀有节点向量优化算法流程图Fig. 3 flow chart of rare node vector optimization algorithm
3 仿真与分析
3.1 硬件木马设计与植入
为了能在硬件木马被激活时快速的判断出硬件木马对电路逻辑功能的修改,硬件木马的负载逻辑直接作用在电路的输出节点,通过观察输出节点的逻辑来判断木马是否已被激活。本文选择的待测电路是学术界公认的 ISCAS’89基准电路中的S1423电路。选择以下四个节点作为触发的稀有节点:G395、G169、G203、G419,其节点为1的概率和翻转概率如表1所示。
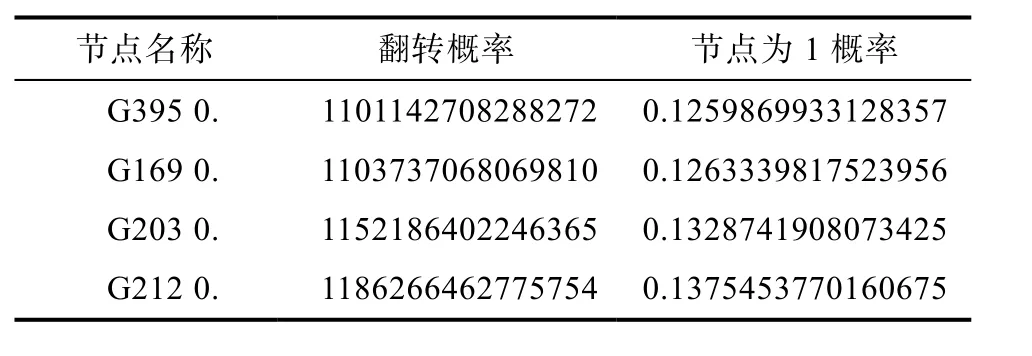
表1 木马输入节点翻转概率情况Tab.1 turnover probability of Trojan horse input node
设计的触发逻辑为最坏情况,所有节点之间选择与门的设计,如图4所示。
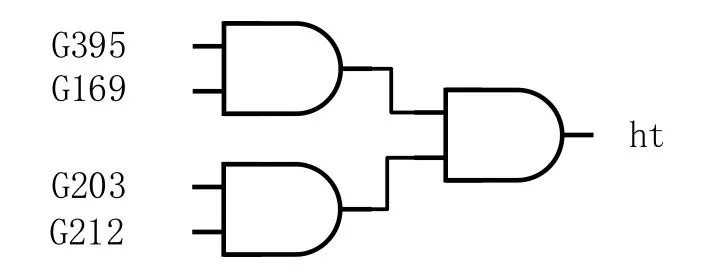
图4 木马触发逻辑Fig. 4 Trojan horse trigger logic
选择负载影响的节点 G727,其转移概率为0.1923496304115702,节点为1的概率为0.25989-50862884521,节点为 0的概率为 0.7401049137-115479。负载逻辑如图5所示,当ht为0时,G727的逻辑值不发生变化;当ht为1时,G727输出的逻辑值发生翻转。硬件木马选择在S1423电路的RTL阶段插入。
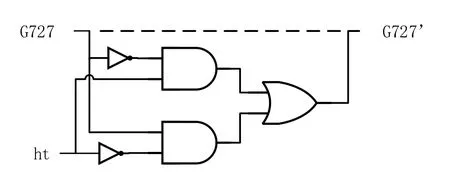
图5 木马负载逻辑Fig. 5 Trojan horse load logic
3.2 优化算法参数确定
为了验证优化算法是否有效,可以根据硬件木马的情况对优化算法的参数进行确定。
(1)Ns确定
由公式(10),Ns可得出 Ns的值至少为 473,优化向量至少能激活一次木马。
(2)阈值θ确定
由于选择的硬件木马翻转概率在0.12以下,为了减少稀有节点的数量,缩短优化时间,对于特定电路,稀有节点的翻转概率阈值θ设置为0.12。通过对稀有节点翻转概率的统计,翻转概率小于0.12的节点数为95,占总数749的12.68%。
(3)优化后向量数T确定
由公式(2)可知,当 Ns至少为 473时,对随机向量集T1的向量数量有一个下限值4 296,而优化后的向量集向量数则不会有该限制,本文将T值确定为5 000。
3.3 实验结果分析
从表 2实验结果可以看出,随机向量集 T1单纯只是随机的0/1序列,共有50 000条向量,向量的内存有781KB,但是木马的激活次数只有16次。由公式(7)可知,当50 000条随机向量做激励时,木马被激活的次数为14.5次,而实际仿真出的木马激活次数大致与计算的激活次数相仿。优化向量集T2由随机向量集T1经优化算法精简而来,如图6所示,左边为优化前的向量集T1,右边为优化后的向量集。选择Ns为434,θ=0.12,T=5 000的输入参数,最终的向量的内存为 78.1KB,为T1的1/10,而T2的最终得到的木马激活次数为521次。

表2 实验结果Tab.2 exp erimental results
图6 向量集T1与向量集T2Fig. 6 Vector set T1 and Vector set T2
从实验结果来看,优化后的向量集T2相对随机向量集T1,向量数减少为原来的1/10,仿真时间缩短为1/10,而激活次数提高了32.56倍。
4 结论
本文提出了基于稀有节点的向量优化算法,达到采用较少的测试向量能够激活硬件木马的目的。完成了向量优化算法的仿真以及向量的测试。仿真表明,能够将随机向量进行优化,使得激活次数提高了 32.56倍,向量数量缩短为 1/10。优化后的向量检测木马效率更高,基于稀有节点向量优化算法效果较好。

