数学问题解答

2021年10月号问题解答

(解答由问题提供人给出)

2626如图D、E、F分别是三角形ABC三边(或延长线)上的点，满足∠ADC=∠BEA=∠CFB，直线AD、BE、CF两两交于点L、M、K，点H是△ABC的垂心.求证：点H是△LMK的外心.

(浙江省慈溪实验中学 华漫天 315300)

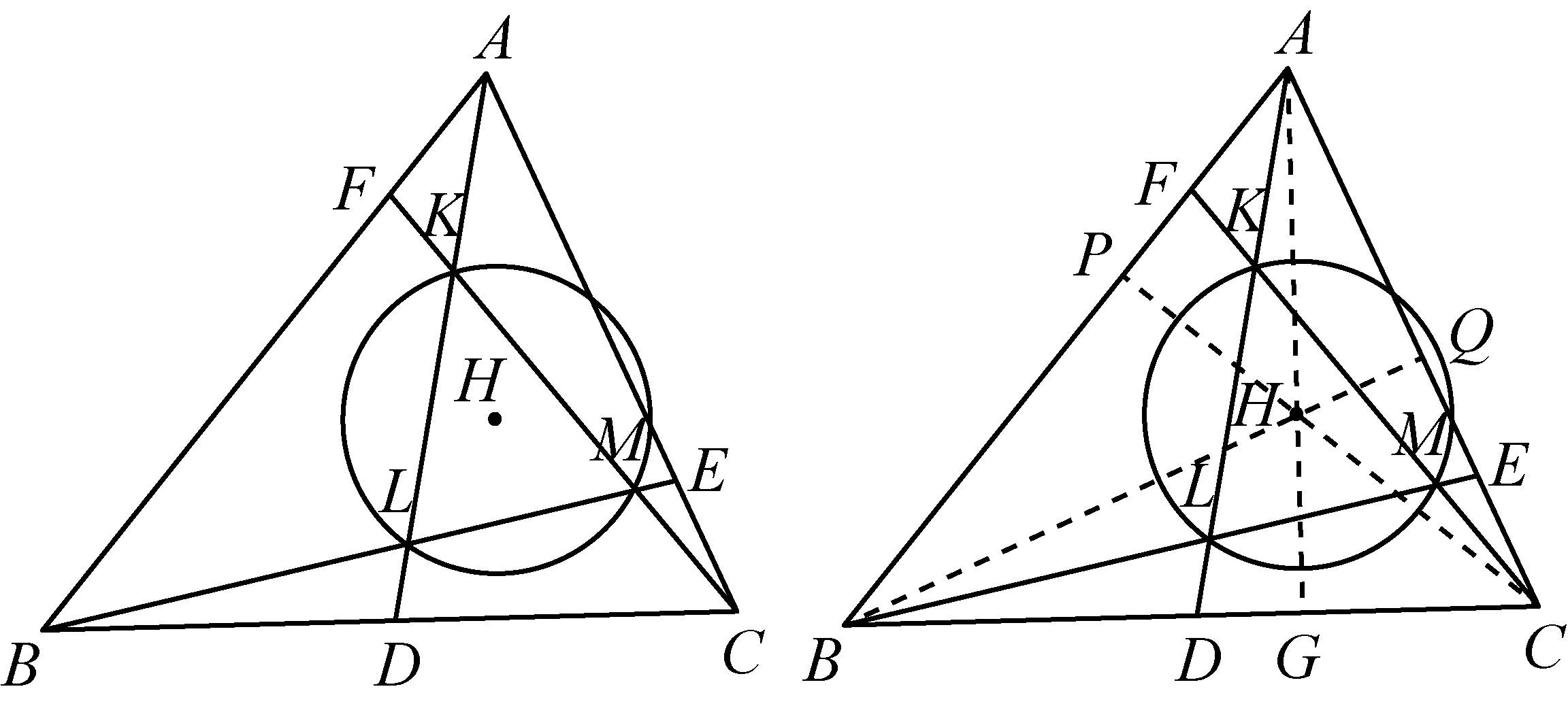
证明作△ABC的三条高线AG、BQ、CP，

由已知不妨令∠DAG=∠EBQ=∠FCP=α，

同时令△ABC的外接圆半径为R，

显然∠BHC=180°-∠BAC，

故△BHC的外接圆直径为

易知A、E、M、F四点共圆，所以

∠BMC=∠EMF=180°-∠BAC，

得B、H、M、C四点共圆，

且外接圆半径就是R，所以

HM=2Rsin∠HBM=2Rsinα;

同理HK=HL=2Rsinα,

即点H是△LMK的外心.

(河南质量工程职业学院 李永利 467001)

证明设△ABC的面积、半周长、内切圆半径分别为△,p,r，旁切圆半径分别为ra,rb,rc.

由察柏尔定理可知OI2=R2-2Rr.

而由数学问题2524题的解答过程可知

于是

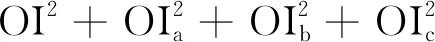
=4R2+2R(ra+rb+rc-r), (2)

又因

△=pr=(p-a)ra=(p-b)rb=(p-c)rc，

a+b+c=2p，

ab+bc+ca=p2+4Rr+r2，

(p-a)(p-b)(p-c)=pr2，

所以

ra+rb+rc

即ra+rb+rc-r=4R, (3)

由(2)，(3)两式可知(1)式成立.

(浙江省海盐县元济高级中学 张艳宗 314300；北京航空航天大学图书馆 宋庆 100191)

≥1等价于

由柯西不等式

即4(a2+b2+c2)+6

由柯西不等式

以上三式相加，

≥a2+b2+2(bc+ca)，

从而a2+b2+c2+3≥a2+b2+2(bc+ca)，

2629设双曲线C的两焦点为F1、F2，两准线为l1、l2，过双曲线上一点P，作平行于F1F2的直线，分别交准线l1、l2于M1、M2，直线M1F1与M2F2交于点Q，则：P、Q、F2、F1四点共圆.

(江西省都昌县第一中学 刘南山 332600)

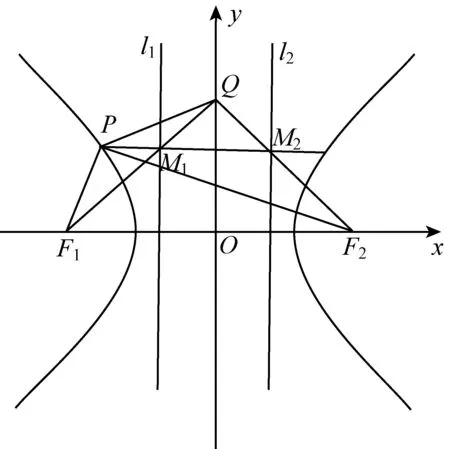
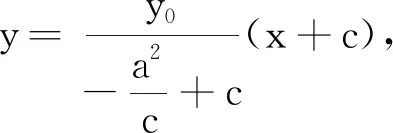
根据对称性知,点Q在y轴上，

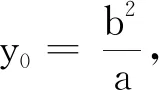
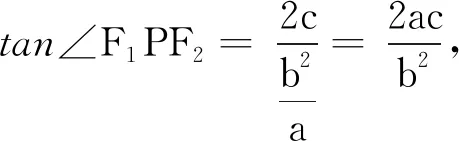
所以∠F1QF2=∠F1PF2，

故P、Q、F2、F1四点共圆.

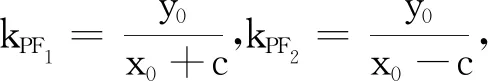
所以∠F1QF2=∠F1PF2，

故P、Q、F2、F1四点共圆.

综上所述，P、Q、F2、F1四点共圆.

2630在ABCD中，M为对角线AC的中点，E、F分别在边AB、BC上，满足∠EMA=∠FMC=∠ADC,O1、O2、O3、O4分别为△EMA、△EBF、△FMC、△ADC的外心.求证：四边形O1O2O3O4是平行四边形.

(陕西省兴平市教研室 吕建恒 713100)

证明设AF与CE交于点K，连结BM，

因为四边形ABCD为平行四边形，

所以∠ADC=∠ABC.

又 ∠EMA=∠FMC=∠ADC=∠EBF，

则M、B、C及M、A、B、F四点分别共圆.

所以∠MCE=∠MBA=∠MFA,

∠MEC=∠MBC=∠MAF.

则M、K、F、C及M、A、E、K四点分别共圆.

所以∠EKA=∠EMA=∠EBF=∠ADC.

则K、E、B、F及K、C、D、A四点分别共圆.

于是 △EMA、△EBF、△FMC、△AADC的外接圆交于一点K.

所以EK、FK、CK、AK分别为⊙O1和⊙O2、⊙O2和⊙O2、⊙O3和⊙O4、⊙O2和⊙O1的公共弦.

则O1O2⊥CE，O1O4⊥CE，

O2O3⊥AF，O1O4⊥AF;

所以O1O2∥O3O4，O2O3∥O1O4;

故四边形O1O2O3O4是平行四边形.

2021年11月号问题

(来稿请注明出处——编者)

(河南省周口师范学院计算机科学与技术学院 李居之 孙文雪 4660011)

2632如图，过圆O外一点Q作圆的切线，切点为点P,N，过点Q作圆的割线交圆于点A,C，过点A作直径ND的垂线交直线CN于点B，直线PN交线段AB于点M，求证：AM=MB.

(山东省泰安市宁阳第一中学 刘才华 271400)

2633如图，两同心圆上任作两割线AXYB和MPQN，求证：AB2+PQ2=MN2+XY2.

(华中师范大学国家数字化学习工程技术研究中心 彭翕成 430079；常州九章教育科技有限公司 曹洪洋 213002)

2634求证：关于x，y的方程2x2+y2=2020没有正整数解.

(山东省临清市北门里街颐清园小区19号楼7单元2楼西户 刘继征 252600)

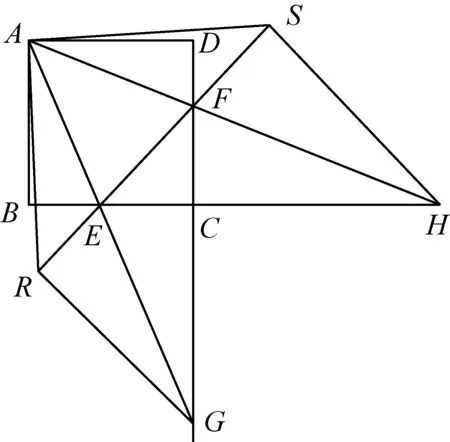
2635如图，正方形ABCD中，E、F分别在边BC、CD上，AE、AF的延长线分别与DC、BC的延长线交于G、H，GR⊥EF于R,HS⊥EF于S,连接AR、AS.∠RAS=90°,△ARS的面积等于正方形ABCD的面积.则∠EAF=45°.

(江苏省无锡市硕放中学 邹黎明 214142)