一种叠前反射地震记录频变速度分析方法

刘 洋,李红星,任弘利,张嘉辉,吴鑫昱

（东华理工大学 地球物理与测控技术学院，南昌 330013）

叠前地震速度分析是反射地震数据处理的重要和必须环节，速度分析的质量直接影响反射地震动校正和叠加成像精度（Stork et al.，1992；Zhang et al.，2006）［1-2］。同时，地震波传播速度作为描述地质体的重要地震属性，也被用来对岩性，尤其是储层性质进行定性和定量解释（Angelos，2006）［3］。传统叠前速度分析只能得到不随频率变化的常速度（Chen et al.，2015）［4］。实际介质中的地震波传播存在频散，尤其在储层及海底介质等典型孔隙介质中（Li et al.，2018）［5］，地震波的频散现象尤为严重。所以，在油气储层地震预测及海底参数声学探测等领域，速度频散成为越来越重要的属性（Aamir et al.，2011；Ahmad et al.，2017）［6-7］。目前叠前速度分析方法主要是基于不同判别准则的叠加速度谱方法（Morozov et al.，1996；Li et al.，2018；Chauris et al.，2017；Li et al.，2018）［8-11］，但是未见直接考虑随频率变化的速度分析方法。笔者提出一种叠前频变速度分析方法，可以利用地震共深度点道集（CDP）获得随频率变化的速度，可为频变速度动校正和叠加以及利用速度频散属性进行储层预测等提供方法支撑。

1 频变速度分析方法

频变速度分析方法利用广义S变换将CDP地震记录由空间-时间域变换到空间-时间-频率域，在每个频率值切片上提取每道地震记录时频谱的极大值，该极大值对应时间-空间关系即为地震道中该频率的反射波时距关系。对每个频率，进行速度扫描，计算每一反射层理论扫描时距曲线，并计算扫描时距曲线和时频谱提取的时距曲线之差的2范数，2范数极小值对应的速度即是该频率地震波的传播速度。反射地震记录频变速度分析方法流程见图1。

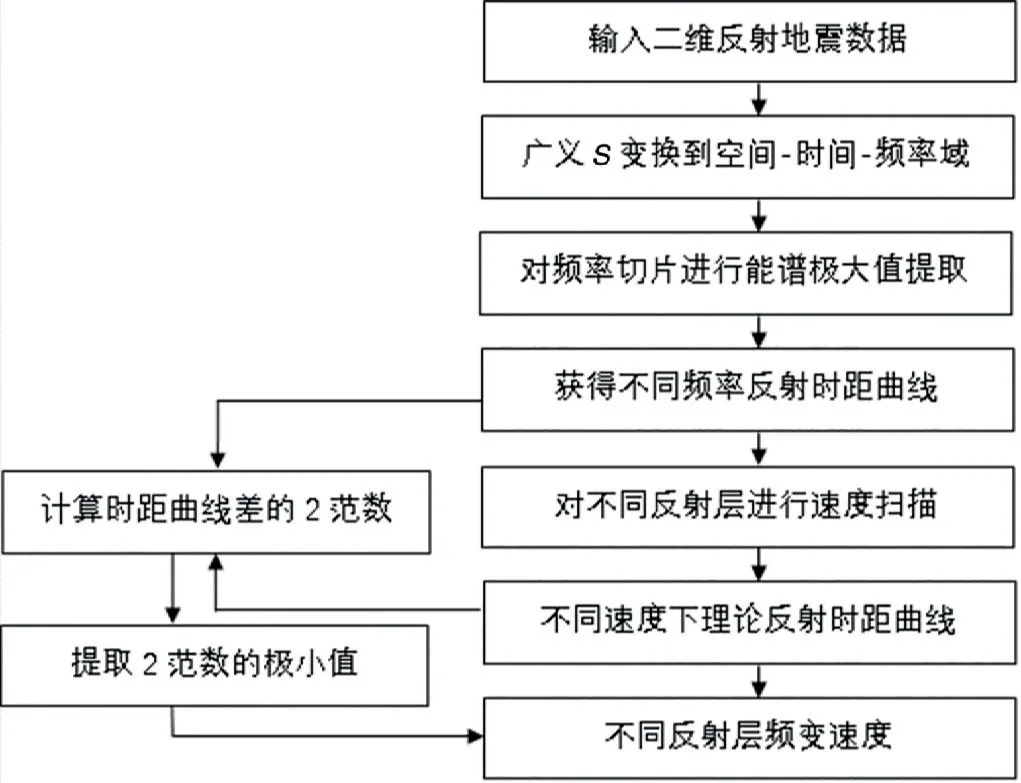
图1 反射地震记录频变速度分析方法流程Fig.1 Flow chart of frequency-varying velocity analysis method for reflection seismic records

反射地震记录u(x，t)的广义S变换为（Hao，2016）［12］

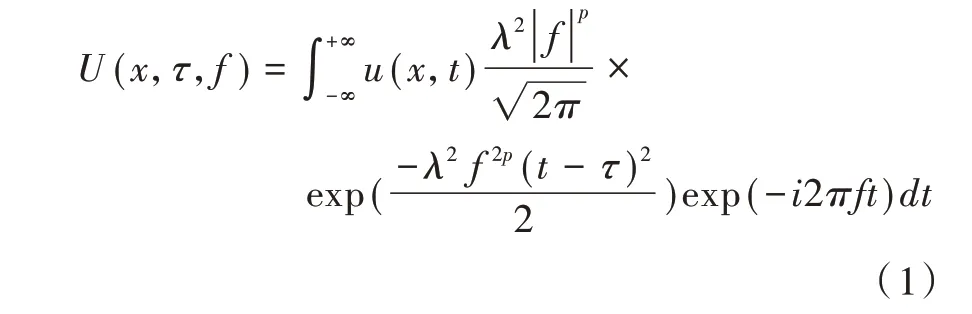
式中：x—地震记录道空间；t—地震记录时间；U(x，τ，f)—空间-时间-频率域地震记录；τ—地震记录时频谱时间；f—频率；λ、p—广义S变换调节参数；exp—e指数。

基于空间-时间-频率谱的每个频率值切片，max函数指的是提取谱值极大值，find函数指的是极大值对应该频率的地震波在不同地震道的旅行时间，也即该频率地震波的时距关系。

式中：[xi，TpF]—频率为FHz的反射地震波在第i地震道的旅行时为TpF；xi—第i道记录的炮检距；U(xi，t，F)—地震记录空间-时间-频率谱在FHz频率处的切片。

根据传统速度分析方法确定频变速度扫描的速度范围，设置速度步长，计算每个速度得到的理论时距曲线与根据时频谱提取的时距曲线差的2范数，2范数的极小值对应的速度即为该频率地震波传播速度。理论时距曲线可表示为：

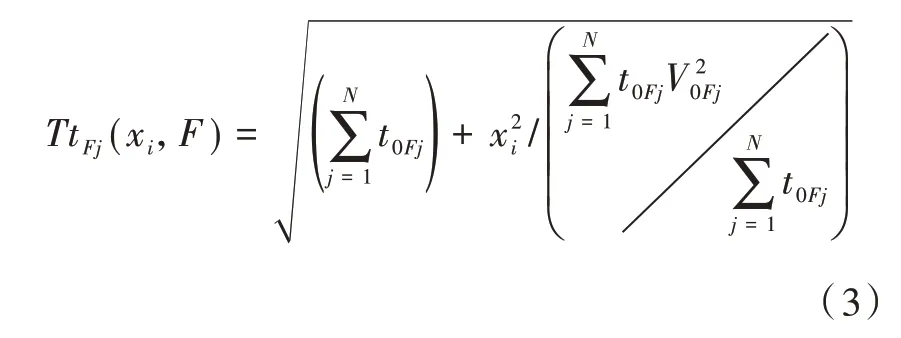
式中：TtFj(xi，F)—频率为FHz的地震波在炮检距为xi的第i道检波器的旅行时；t0Fj—频率为FHz的地震波在第j个反射层内的单程旅行时；V0Fj—频率为FHz的地震波在第j个反射层处的传播速度。理论时距曲线与提取的时距曲线差的2范数表示为，范数的极小值对应的速度即为某频率地震波传播速度。min函数指的是范数取得最小值。

2 频变速度分析方法的模型验证

为了验证本文提出的频变速度分析方法的正确性，设置模型，模拟地震记录，应用本文方法计算频变速度，和模型设置的频变速度进行对比。模型1为单反射界面介质模型，地层的速度为830 m/s，反射地震记录如图2所示。

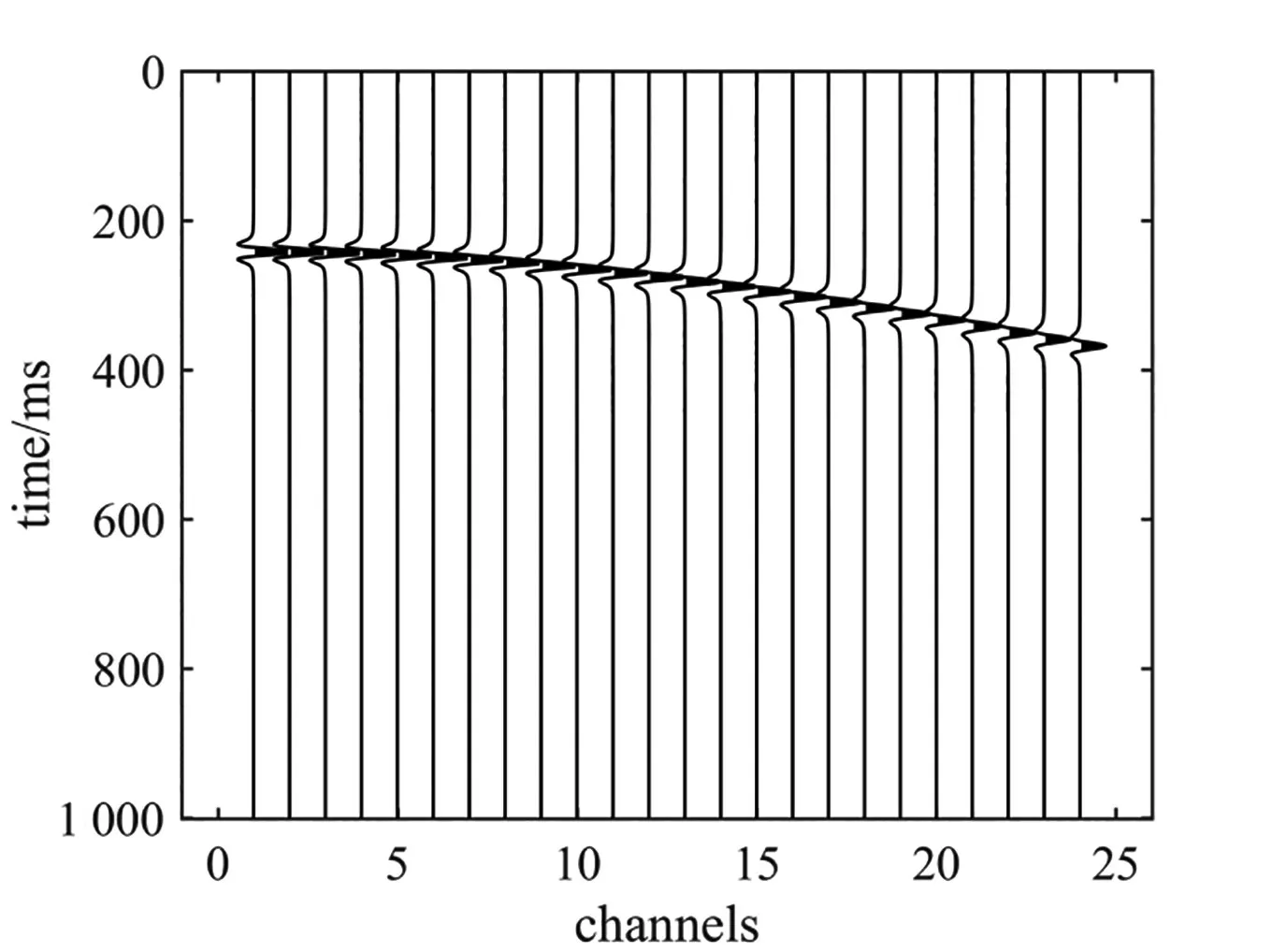
图2 模型1的反射地震记录Fig.2 Reflection seismogram of Model 1

从地震记录第1道的广义S变换时频谱（图3）可看出，地震记录的主频为50 Hz，频带范围为0～150 Hz左右，低频的时间分辨率比高频的时间分辨率低。因为地震波速度设置不随频率变化，所以时频谱中每个频率谱值的峰值对应的时间位置是一致的。提取空间-时间-频率谱的某一频率切片能谱值的极大值，得到该频率地震波的时距曲线（图4）。通过对不同频率地震波进行速度扫描，计算理论时距曲线与拾取时距曲线差的2范数，获得拟合频率-速度谱，提取其极值，可以获得频率-速度曲线，也即频变速度（图5中“*”号）。本文提出的频变速度分析方法获得的频变速度和模型1给定的速度高度吻合（图5），证明了本方法的正确性。

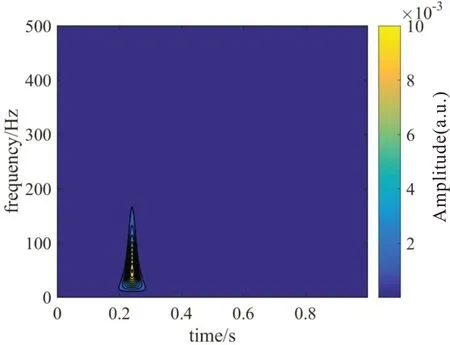
图3 模型1第1道地震记录时频谱Fig.3 Spectrum of the first seismic record in Model 1

图4 模型1的空间-时间-频率谱50 Hz切片及谱峰值对应的50 Hz时距曲线（+号）Fig.4 The 50 Hz slice of space-time-frequency spectrum of Model 1 and 50 Hz time interval curve（+sign）corresponding to spectral peak value

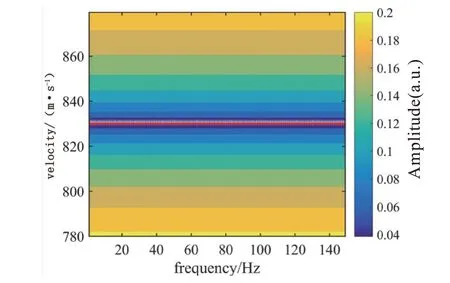
图5 模型1频变速度分析结果（*）及模型1给定速度（红线）Fig.5 Analysis results of frequency-varying velocity（*）of Model 1 and given velocity（red line）of Model 1

Amplitude(a.u.)

为了进一步验证方法的适用性，设置模型2，模型2给定的速度为频变速度，速度与频率的关系为：

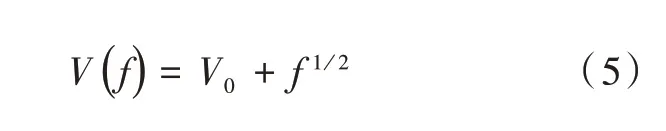
式中，V0取值为800 m/s，频率按照子波频带范围取值为0～150 Hz。

由于模型2采用频变速度，模型2的地震记录（图6）波形显示出波谷的不对称特点，每道的时频谱中每个频率谱值的峰值对应的时间存在细微差别（图7）。利用本文频变速度分析方法获得的频变速度和模型2给定的速度基本吻合（图8），本方法获得的频变速度略高于模型2给定的频变速度，证明了本方法在频变速度模型情况下的适用性。

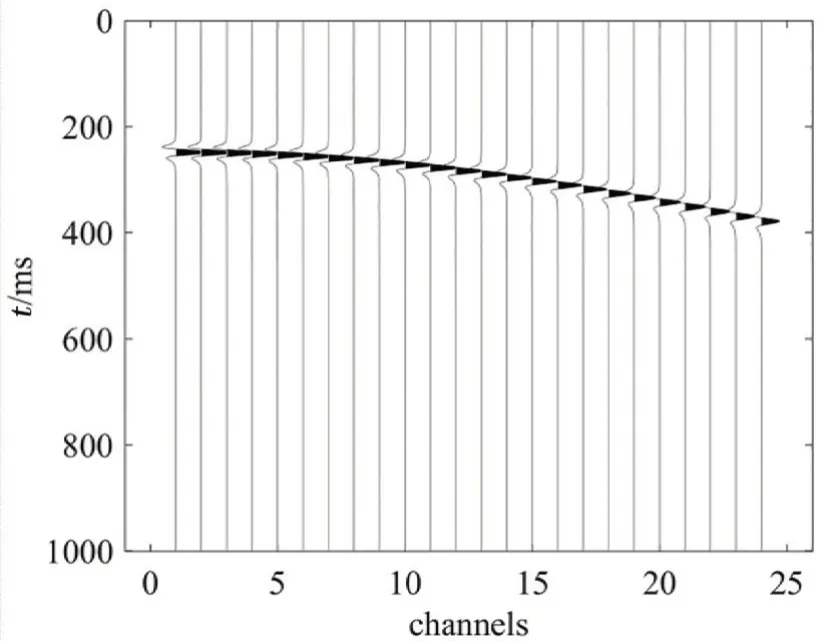
图6 模型2的地震记录Fig.6 Seismogram of Model 2

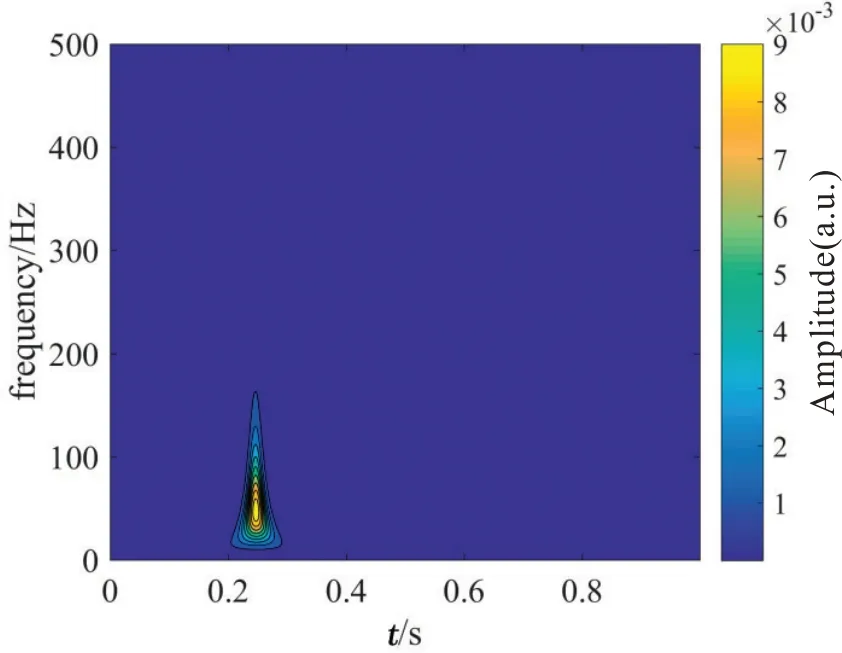
图7 模型2地震记录第1道时频谱Fig.7 The first time spectrum of Model 2 seismic record

图8 模型2频变速度分析结果（*）及模型2给定速度（红线）Fig.8 Analysis results（*）of frequency-varying velocity of Model 2 and given velocity（red line）of Model 2

为了进一步验证方法的实用性，设置模型3，模型3为两层反射地震模型，第一层速度为不随频率变化的恒定速度780 m/s，第二层速度为频变速度，频变速度规律与模型2一致，V0为830 m/s。模型3地震记录（图9）第二层反射波形由于频变速度显示出波谷的不对称特点，且利用本频变速度分析方法获得的频变速度和模型3给定的速度基本吻合（图10），第二层频变速度略高于模型3给定频变速度，证明了本方法在多水平反射层情况下的实用性。

图9 模型3地震记录Fig.9 Seismogram of Model 3

图10 模型3频变速度分析结果（*）及模型给定速度（红线），Fig.10 Analysis results（*）of frequency-varying velocity of Model 3and the given velocity（red line）of the model，

3 结论

基于时频分析技术，提出了一种反射地震记录频变速度分析方法，其可以利用地震共深度点道集获得随频率变化的速度。同时，建立了单层常速度、单层频变速度以及上覆常速度和下伏频变速度地层三种不同的地质模型，开展了模拟地震数据测试。结果表明，本方法可以获得准确的常速度地层速度及比实际频变速度率高的地层频变速度，使利用频变速度开展更精确的动校正和储层预测成为可能。