一绳法的应用与计算推导

刘 磊

（中国铁路上海局集团公司杭州工务段，线路技师 浙江 杭州310009）

在整正现场曲线时，我们通常采用简易拨道法、直股支距法、绳正法、综合法等方法拨道使曲线圆顺。当遇到9 号及以下小号码道岔导曲线、岔后连接曲线较短（小于50 m）和小半径短曲线的整正养护，我们也可以选用一绳法。由于小曲线长度不一、现场情况的差异，选奇数中点等分段还是偶数中点等分段，需根据现场情况具体分析后作出正确选择。

1 一绳法概述

一绳法，也称长弦矢距法，即把整个小曲线从头至尾拉一根弦绳等分成n 份，以等分点的计算矢距之差来拨正曲线，使曲线圆顺的一种拨道方法。

2 一绳法的整正原理

曲线圆度通常是用半径来表达，如果一处曲线，其圆曲线部分各点半径完全相等，那就说明这处曲线是圆顺的。但是铁路曲线半径都是很大的，现场无法用实测半径的方法来检查曲线圆度，通常以曲线半径（R）、弦长（L）、正矢（f）的几何关系来检验，图1 为曲线半径、弦长、正矢关系示意图。

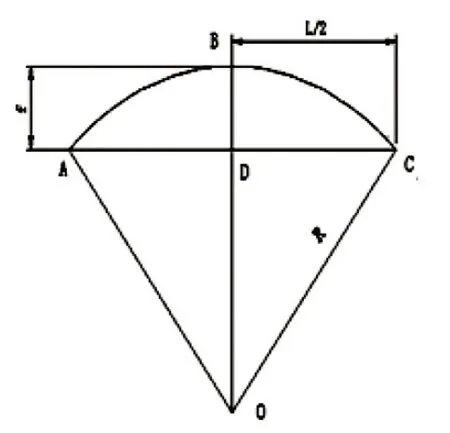
图1 曲线半径、弦长、正矢

曲线半径、弦长、正矢之间的关系为：

3 一绳法的具体步骤与计算过程

3.1 步骤与方法定出曲线中点，量取曲线中点的正负值，计算切线长，确定曲线头、尾位置。具体方法如下：

1）拉弦绳和用眼看，将曲线外股两端的直线段（延钢轨工作边）延长，得到交点，再由交点顺着延长线往回量一切线长，便得曲线头、尾。

2）在切线交点外打一木桩，在木桩上画出交点J，用2 m（或4 m、6 m、8 m……）长度，定出A、C 两点，假设A、C 两点距离为2 m，且A 点到交点距离等C 点到交点距离，即JAO=JCO。再分出A、C 两点的中点，量出AD的距离。

3）利用以下公式计算：

切线长=半径×系数

3.2 任意等分弦绳矢距计算图2 为任意等分弦绳矢距示意图。

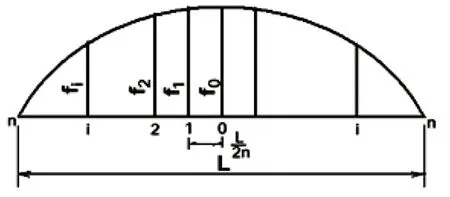
图2 任意等分弦绳矢距示意图

1）通常按8 等分或10 等分进行弦长偶数等分，则由曲线中点0 向两端按等分段数排成1、2、3、4、5……n/2 点号，按点号计算矢距（n≥2）。弦长等分8或10 段等分点矢距（fn）与中点矢距（f0）的倍数见表1。

表1 弦长等分8或10段等分点矢距（fn）与中点矢距（f0)的倍数表

2）当采用7或9等分进行弦长奇数等分，则由曲线中点0 向点号1 半等分，点号1 向两端按1 等分段数排成1、2、3……（n-1）/2+1 点号，按点号计算矢距（n＞2）。弦长等分7 或9 段等分点矢距（fn）与中点矢距（f0）的倍数见表2。

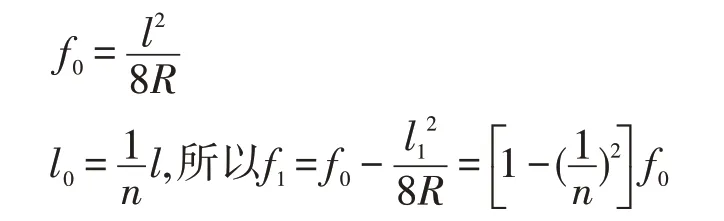
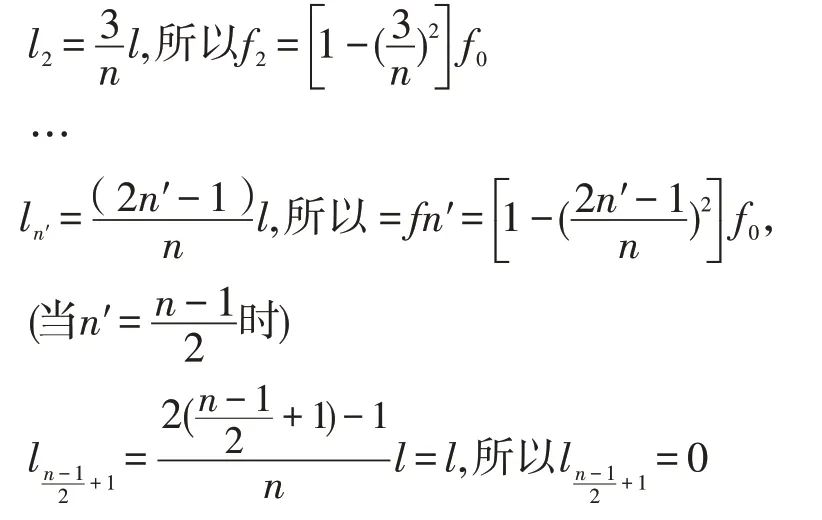
表2 弦长等分7或9段等分点矢距（fn）与中点矢距（f0)的倍数表

3）改正量计算。矢距为曲线上股工作边至弦绳内侧的垂直距离。

改正量=计算矢距-实量矢距

结果为“+”号需上挑，“-”号需下压。

改正量计算完成，就可进行现场拨道或改道，从曲线头至曲线尾钢轨上股作用边拉一弦绳作为基准线，将各等分点的矢距按计算矢距值改正。

4 现场应用

4.1 确定矢距改正量现场某一道岔岔后附带曲线，10 等分弦长，现场（一）实测各点矢距如图3 所示，求各点计算矢距及各点矢距改正量。

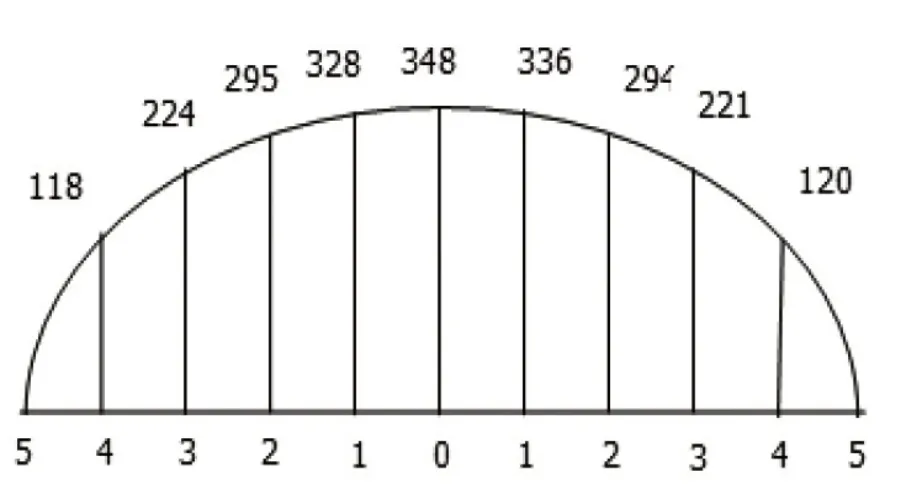
图3 现场（一）各点矢距图

1）道岔辙叉角一般已知，不知现场直接测量。先将道岔及附带曲线前后直线拨直，然后用两条绳拉出切线交点：一条沿附带曲线外直线外股钢轨，另一条沿道岔辙叉后钢轨，分别沿外股钢轨非作用边拉直线，两绳的交点就是切线点。

切线长=半径R×tan（a/2）

2）根据导曲线的长短，把弦分成10 等分，现场量出f0到f3共10点矢距，并计算出各点计划矢距。

当弦长10等分时（即n=10）：

现场各点的改正量如下：

4.2 确定导曲线改动量现场（二）某9 号道岔导曲线，导曲线曲线半径R 为18 m，从导曲线始点至导曲线终点之间拉一根弦绳等分成7 段，弦长为13.793 m，求导曲线各点的改动量。现场（二）各点矢距如图4所示。

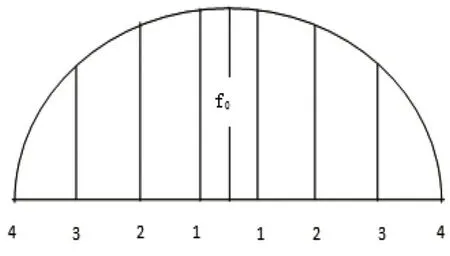
图4 现场（二）各点矢距图

1）尖跟第一个支距点垂直到导曲线上股上为导曲线实际始点，支距终点用方尺方到导曲线上股为导曲线终点。从导曲线始点至导曲线终点之间拉一根弦绳就是弦长。

2）根据导曲线的长短，把弦分成7 等分，如图4所示，现场量出f0到f3共7 点矢距，并计算出各点计划矢距。

3）各点计算矢距与现场各点矢距之差，就是导曲线各点的改动量。

5 结束语

现场实践证明，选用一绳法整正9 号及以下小号码道岔导曲线以及岔后连接曲线较短（小于50 m）和小半径短曲线，经过一段时间列车运行，曲线圆顺度保持较好。通过对一绳法的偶数中点等分弦长和奇数中点等分弦长的计算公式推导后，相比绳正法、支距法等其它方法，不仅计算更简单、易掌握，而且工作量小、节省作业时间、曲线拨后效果更明显。值得推广使用。