多重Laplace-Stieltjes变换的两个等式

毕家烨，霍颖莹

（广东工业大学 应用数学学院，广东 广州510520）

L-S变换和其他积分变换密切相关，包括Fourier变换和Laplace变换，同时也是Dirichlet级数的推广，它是求解某些积分方程的有力工具，同时在概率论中也有应用。中外数学工作者在L-S变换和有关方面，已经取得了许多重要成果。1937年，文献[2]研究了二重L-S变换在有界收敛区域内的解析性。1941年,文献[3]深入研究了二重L-S变换的收敛区域，给出二重L-S变换相关收敛横坐标的定义及讨论了二重L-S变换的逆变换。1962年，余家荣[4]得到了二重Dirichlet级数和二重L-S变换相关收敛横坐标的计算公式。2009年，梁美丽等[5]定义了n重Dirichlet级数并研究了其收敛区域和增长性。孔荫莹等[6]总结了大量(一维)L-S变换的研究，关于L-S变换及Dirichlet级数的最新研究，可以参考文献[7-10]。

本文将得到关于L-S变换的两个等式，其中一个推广了Dirichlet级数中的相应结论，另一个与内积空间中的Parseval等式类似。建立这2个等式，需要Vitali有界变差函数的一些性质，为方便起见，将给出Vitali有界变差函数的定义，首先引入一些术语和记号。

1 定义

定义1对(n元)复值函数f，若f在[u,v]上有定义，则映射f→∆(f,[u,v])由下式给出。

2 引理

3 定理及证明

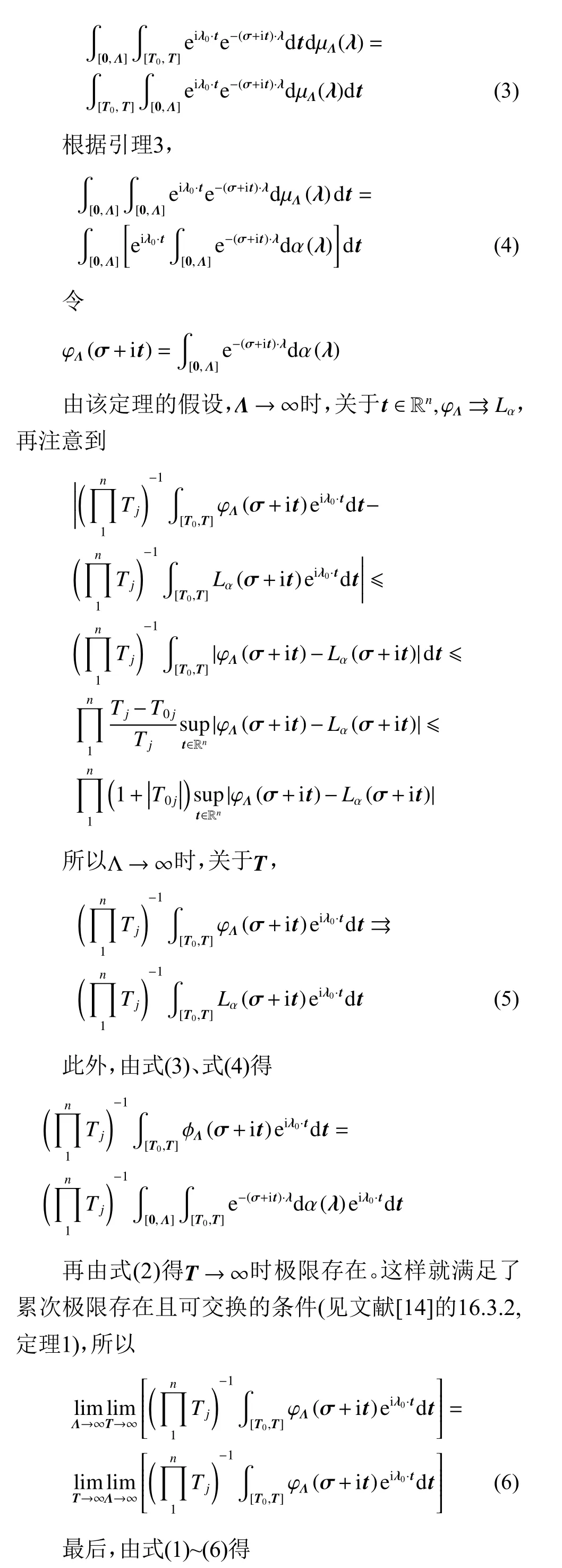
这样就满足了累次极限存在且可交换的条件(见参考文献[14],16.3.2,定理1)，所以

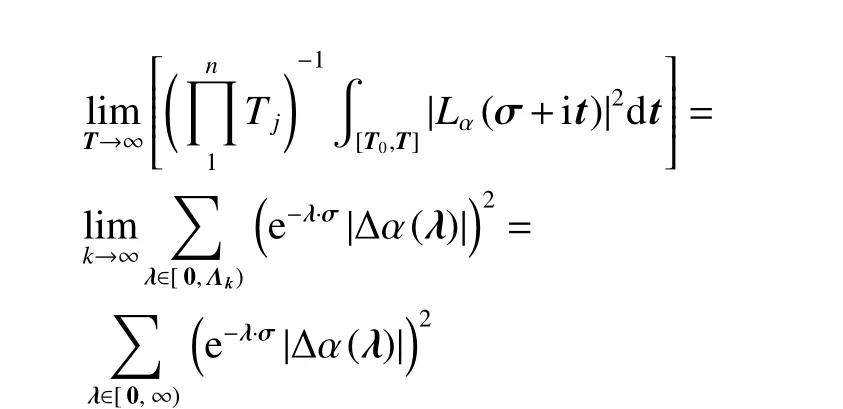
4 注记