基于排队论的旅游景点停车问题分析

郝志香

太原科技大学，山西太原 030024

引言

近年来，“停车难”已成为城市的通病。随着人们生活水平的提高，旅游也成为人们生活中不可或缺的一部分，其中自驾出游人群所占比重逐渐上升，给景区停车场带来了不小的压力。因此，景区需要一个优化停车配置，来解决停车问题。本文将通过排队论来建立旅游景区停车模型。

一 模型建立

（一）景区内停车问题描述

对于一个建有停车场的旅游景点来讲，淡季时停车问题可以忽略不计，而在旅游旺季时，寻找停车位往往很困难，从来出现排队的现象[1]。对排队论而言，有三个基本的组成部分：输入过程，排队规则，服务机构。以下将说明各部分在景区停车的特征。

输入过程，即指游客（车辆）按照怎样的规律到达排队系统。对于景区停车系统来讲，游客源是无限的，游客到来的方式是一个一个依次到达，一定时间的到达数服从泊松（Poisson）分布[2]。

排队规则，指游客到达排队系统后按照怎么的规则和方式接受服务。对于景区停车系统而言，当车辆到达后可能直接找到或者通过巡游找到空闲停车位，当发现没有空闲停车位时，车辆可以选择等待（等待制），也可以随机离去（损失制）。

服务机构，一般指服务台的数量、服务方式以及服务时间的分布。对于景区停车系统而言，一个停车场入口可以看作是一个服务台，并假设该入口为自动识别系统，会显示剩余停车位数量。车满则自动关闭。

从以上分析可以看出，景区停车可以看作是M/M/C/N/∞/FCFS（N≥C）的情形。

（二）模型假设

景区停车 M/M/C/N/∞/FCFS（N≥C）的模型假设：1.游客到达过程服从参数为λ的泊松分布。2.游客服务的时间（即停车时间）服从参数为μ的负指数分布。3.服务系统共有C个服务台，即有C个停车场，系统容量为N（N≥C）。4.游客源是无限的。5.服务方式为先到先服务（即FCFS）。6.游客到来的方式、服务的时间以及各服务台的工作都是相互独立的（不搞协作），且平均服务率相同。7.输入过程与服务时间的分布总假定是平稳的，即分布的期望值、方差等参数不受时间的影响。

（三）模型建立

1 符号说明

λ—游客平均到达率；1/λ—游客到达的平均间隔时间；μ—游客平均服务率；1/μ—游客的平均服务时间；ρ=λ/cμ—停车系统的服务强度或泊车位的平均利用率，只有当λ/cμ<1时才不会排成无限的队列；n—稳态系统中任一时刻状态，即系统中所有游客数；Ls—系统中的平均游客数，即队长；Lq—系统中排队等待的平均游客数，即排队长；Ws—系统中游客的平均逗留时间；Wq—系统中游客的平均排队等待时间。

2 模型建立与求解

根据模型理论[3]，列出状态概率的稳态方程：

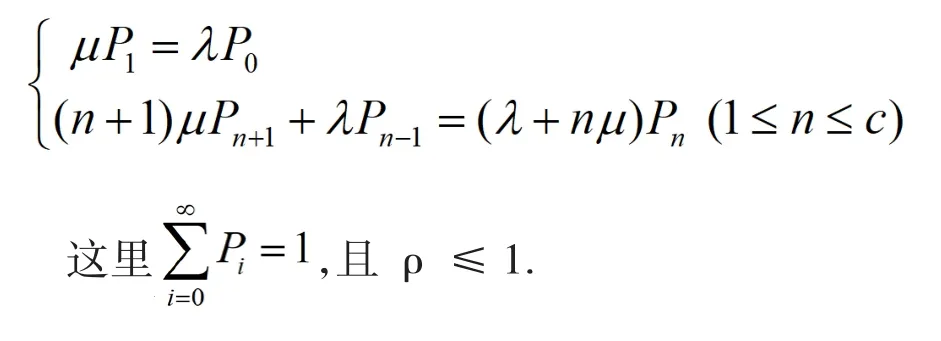
从而得状态概率：

其中Pk就是游客被拒之于系统之外的概率，成为损失率。

系统的运行指标求得如下：

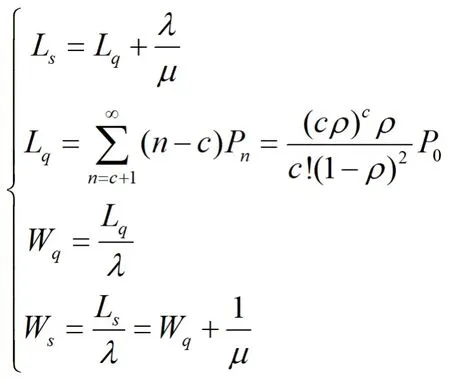
3 优化分析

在一般情形下，提高停车场的停车效率必然会降低游客的等待费用（损失），但却常常增加了景区停车场的服务成本，我们最优化法目标之一是使二者费用之和为最小[4]。在稳态情形下，单位时间全部费用（服务成本与等待费用之和）的期望值Z=Cs·C+Cw·L，其中C是服务台数，Cs是每服务台单位时间的成本，Cw为每个游客在系统停留单位时间的费用，L是系统中游客平均数Ls或队列中等待的游客平均数Lq（它们都随着C值的不同而不同）。由于Cs和Cw都是给定的，唯一可能变动的是服务台数C，所以Z是C的函数Z（C），现在就是要求最优解C*使Z（C*）为最小。

二 景区案例分析

某景区欲建一停车场，现提供旺季资料如下：游客按照参数λ=60车/小时的Poisson流到达停车场，游客服务的时间（即停车时间）服从参数为μ=50车/小时的负指数分布，每个服务设备单位时间的成本为5元/小时，每个游客在系统逗留单位时间的损失成本为10元/小时，试确定最佳的C*，使得单位时间内的平均总费用最低[5]，具体停车时长与费用明细如表1、表2。

表1 车流量与停车时长关系表

表2 游客数与停车总费用关系表

落在区间（0.0783,0.5809）内，所以C*=3，此时总费用Z（C）最小。

当C*=3时，整个停车场的空闲概率为

平均队长

平均等待时间与逗留时间

三 结语

对于景区而言，有效解决停车问题可以增加游客数量，并提高景区的知名度。本文首先介绍了排队论的一些基础概念，然后将景区停车看成是一个多服务窗混合制排队系统[6]，建立了模型，对景区停车效率进行了研究。当景区停车场的服务成本和游客的等待费用之和为最小时，停车场的停车效率达到最优，此时的停车场数量也为最优。