爆炸荷载下钢管混凝土构件动态响应的数值模拟与试验验证*

蔡鹏飞，熊祖钊,蔡路军

(1.武汉科技大学 理学院，武汉 430065；2.中铁广州工程局-武汉科技大学爆破技术研究中心，武汉 430065)

近年来，易燃易爆化学品爆炸导致的重大安全事故时有发生，建筑物的抗爆防爆设计研究成为一项重要而又迫切的攻关课题。钢管混凝土组合结构是一类被证明具有良好承载能力及抗震性能的结构形式。一方面，钢管对核心混凝土的套箍作用，使核心混凝土处于三向应力状态之下，受约束混凝土的强度得以大大提高，塑性韧性性能得到全面改善；另一方面，核心混凝土能够延缓或避免外包钢管过早的发生局部屈曲，进而确保更好的发挥该材料力学性能[1]。钢管混凝土结构在静力、长期往复、抗火、抗震、钢管初应力以及粘结滑移方面的研究已经有了比较成熟的成果问世，然而，其在爆炸冲击荷载作用下的力学性能研究有待加强。

OmarI Abdelkarim等利用LS-DYNA有限元软件研究了FRP-混凝土-钢管组合柱在车辆碰撞作用下的受力性能，分析了混凝土无侧限抗压强度、材料应变率、长径比、FRP约束比率、轴向以及水平荷载等多个参数对其力学性能的影响[2]。Jing Dong等人研究了爆炸荷载作用下FRP约束钢管混凝土柱的动力响应，详细讨论了FRP层数、混凝土强度和截面尺寸对钢管混凝土柱抗爆性能的影响。结果表明：FRP约束有效地提高了柱的抗爆性能，易损件主要出现在柱的中部和两端。通过增加FRP层数或混凝土强度，可以提高柱的抗爆性能[3]。史艳莉等通过耦合ABAQUS有限元软件建立了钢管混凝土构件在不同温度下的侧向撞击有限元模型,分别对不同温度下的挠度和撞击力时程曲线进行对比,结果表明:温度对钢管混凝土构件的侧向撞击性能影响明显,随着温度升高,构件跨中挠度大幅增加,撞击时程变长;高温下构件的撞击力时程曲线与常温下差异明显,随着温度升高,构件的抗撞击性能逐渐降低,当温度超过400 ℃后,构件抗撞击性能损失严重[4]。Fujikura S等通过爆炸试验研究了钢管混凝土管桥墩的动力反应，并采用单自由度动态分析和纤维基础动态分析两种方法对钢管混凝土柱的最大残余变形试验值进行了校准,建立了考虑压力折减等因素的最大位移计算方法[5]。Hongwei Wang等人研究了近距离爆炸荷载作用下钢管混凝土柱的抗爆性能和剩余强度，分析了装药量、钢管厚度和截面形状对钢管混凝土柱动力响应的影响[6]。刘兰等人研究了纤维增强复合材料约束钢管混凝土轴心受压柱的抗爆性能，结果表明：轴压比不超过0.5时，轴压力的存在能提高试件的抗爆性能，而轴压比超过0.5以后，轴压力的存在会极大地削弱试件的抗爆性能[7]。孙珊珊等人设计了大比例钢管混凝土墩柱静爆试验，获得了钢管混凝土墩柱柱面爆炸荷载的压力分布规律,对比研究了各经验公式(入射压力、反射压力和正压持时等)的预测差异与适用性[8]。目前，国内外针对钢管混凝土结构的抗爆研究主要集中于远距离爆炸和组合层结构，对近距离爆炸下钢管混凝土的破坏形式研究较少；且由于爆炸试验的受限性，大多的数值模拟研究没有具体的试验支撑。

通过数值模拟与试验相结合的方法对爆炸荷载下钢管混凝土的动态响应进行研究。运用LS-DYNA有限元软件，采用多物质流固耦合的方法建立爆炸载荷作用下钢管混凝土构件模型，并于武汉科技大学校内中铁广州工程局-武科大爆破技术研究中心的空气爆炸罐中进行了具体的近距离爆炸试验。基于可靠的试验数据来验证数值模型的有效性及合理性，在此基础上通过数值模拟对混凝土强度、钢管壁厚等影响钢管混凝土结构抗爆性能的参数进行更为深入的研究分析。

1 有限元模拟方法

1.1 有限元模型的建立

参考《钢管混凝土结构技术规范》，并按照相似原则分别考虑了物理相似，几何相似，刚度相似等条件，最终确定试件的尺寸为：长1200 mm，钢管截面的边长120 mm，厚度3 mm，炸药放置在柱中心表面，通过改变炸药模型的体积来控制药量大小。

钢管采用shell163壳单元，混凝土、空气、炸药均采用solid164三维实体单元，钢管和混凝土中部400 mm位置的单元大小为4 mm，其他位置单元大小为6 mm；空气单元大小为10 mm，求解时间控制为2 ms。网格模型如图1所示。

图 1 网格模型Fig. 1 Grid model

钢管与混凝土的接触通过*CONTACT_TIED_SURFACE_TO_SURFACE关键字定义，接触对象为接触面上的节点组元[9]。爆炸冲击波与钢管混凝土柱之间相互作用通过关键字*CONSTRAINED_LAGRANGE_IN_SOLID多物质流固耦合法的方法进行模拟，因钢管为壳单元，混凝土为实体单元，所以需分开定义它们与流体网格的耦合关键字。

采用流固耦合算法模拟爆炸冲击波和结构、构件相互作用时，需要定义一个有限空气域[10]，且为了避免边界处冲击波的反射对求解域的影响，可以对有限空气域表面施加无反射边界条件来模拟无限大的空间。无反射边界条件通过边界表面节点组元施加，并且需考虑膨胀波和剪切波被吸收的影响。另外，为了模拟实际工况，将柱两端钢管面上50 mm长度的节点的所有自由度约束，并考虑钢管和混凝土单元的自重。

最后在k文件中加入关键字*MAT_ADD_EROSION来定义混凝土材料的失效删除，其中混凝土采用第三主应变极限值mneps控制受拉失效和第一主应变极限值mxeps控制受压失效。钢管的破坏通过材料模型的失效应变参数FS控制。

1.2 材料类型

1)钢材材料模型

钢材属于应变率敏感材料，随着应变率的增大，它的动态屈服强度和瞬时应力等部分材料属性会显著提高。选用*MAT_PLASTIC_KINEMATIC非线性塑性材料模型来描述构件中钢管的动态特性，该材料模型适用于包含应变率效应的各向同性塑性随动强化材料[11,12]。

钢管采用Q235号钢材，计算中材料参数如表1。

表 1 *MAT_PLASTIC_KINEMATIC关键字参数设置Table 1 *MAT_PLASTIC_KINEMATIC Keyword parameter setting

其中:RO为材料密度；PR为泊松比；E和G分别为弹性模量和剪切模量；F为材料屈服强度；C、P为考虑应变率效应的参数；FS为材料失效时塑性应变。

2)混凝土材料模型

采用LS-DYNA中提供的111号材料模型*MAT_JOHNSON_HOLMQUIST_CONCRETE来定义混凝土的本构关系。该模型综合考虑了高应变率、大应变、高压效应，其等效屈服强度是应变率、压力及损伤的函数，而压力是体积应变(包括永久压垮状态)的函数，损伤累积是塑性体积应变、等效塑性应变及压力的函数[13-15]。计算中采用C30等级混凝土，材料参数如表2。

表 2 *MAT_JOHNSON_HOLMQUIST_CONCRETE关键字参数设置Table 2 *MAT_JOHNSON_HOLMQUIST_CONCRETE Keyword parameter setting

其中:RO为密度；G为剪切模量；A、B、C、N为材料强度参数；Fc为静态单轴抗压强度；T为最大拉伸静水压力；EFMIN为最小开裂塑性应变；PC和PL分别为压实压力和完全压碎压力；UC和UL分别为与其对应的体积应变；D1和D2为损伤系数；K1、K2、K3为材料压力常数。

3)空气材料模型及状态方程

假定空气为无黏性的理想气体，冲击波的膨胀过程为等熵绝热，本文采用材料模型*MAT_NULL以及*EOS_LINEAR_POLYNOMIAL状态方程加以描述[16]。材料参数如表3所示。

表 3 空气材料及状态方程参数Table 3 Air material and equation of state parameters

其中:RO为密度；C0～C6为状态方程系数；E0为初始内能；V0为初始相对体积。

4)炸药材料模型及状态方程

采用LS-DYNA提供的8号炸药材料模型*MAT_HIGH_EXPLOSIVE_BURN及其状态方程*EOS_JWL模拟TNT炸药的爆轰过程，参数设置如表4、表5所示。该状态方程是一种不显含化学反应、由试验确定参数的动力学半经验状态方程，能较准确地描述爆轰产物的膨胀驱动做功过程[17,18]。

表 4 *MAT_HIGH_EXPLOSIVE_BURN关键字参数设置Table 4 *MAT_HIGH_EXPLOSIVE_BURN Keyword parameter setting

表 5 *EOS_JWL关键字参数设置Table 5 *EOS_JWL Keyword parameter setting

其中:RO为炸药密度;D为爆速;PCJ为爆压;A、B、R1、R2、ω为炸药性能参数;E为单位体积内能;V为相对体积。

2 试验验证

为了验证数值模拟方法的有效性，制作了3根相同的钢管混凝土试件进行爆炸破坏试验。试件S1、S2、S3长度为1200 mm，截面边长120 mm，钢管壁厚3 mm，混凝土强度等级为C30，如图2所示。整个试验都在武汉科技大学爆破技术研究中心的爆炸罐中进行，炸药悬挂于试件中心位置，每根试件进行药量从少到多的4次重复爆炸试验，每个试件仅第4炸药量不同，试验工况如表6所示。爆源为乳化炸药，导爆管雷管引爆，试件采用钢架反力支撑系统进行固定，试验布置如图3所示。为记录试件受爆炸荷载过程中加速度变化情况，在试件背爆面布设3个加速度传感器，测点A1、A2、A3距中心位置距离分别为0 mm、20 mm、40 mm。

图 2 试件实物图Fig. 2 Real sample

图 3 试验布置图Fig. 3 Test layout

表 6 试验工况Table 6 Test conditions

2.1 残余变形对比

将构件残余变形值的模拟结果与试验结果进行对比，如表7所示。在爆炸载荷作用下，钢管混凝土构件的数值模拟破坏形态与试验破坏形态基本一致，均发生了明显变形。工况S1-4爆坑深度为12.2 mm，模拟结果为11.32 mm，误差7.2%，试件中心的两侧鼓包不明显，如图4所示；工况S2-4和工况S3-4爆坑深度分别为15.2 mm、19.5 mm，模拟结果分别为14.07 mm、18.79 mm，误差分别是7.4%、3.6%(图5、图6)；且工况S3-4产生了明显的弯曲变形，试件背爆面中心挠度为5.2 mm，模拟结果为5.09 mm，误差为2.1%。对于爆炸试验，模拟误差均在10%以内，说明数值模拟方法可以有效地模拟钢管混凝土构件在爆炸冲击荷载下的动态响应。

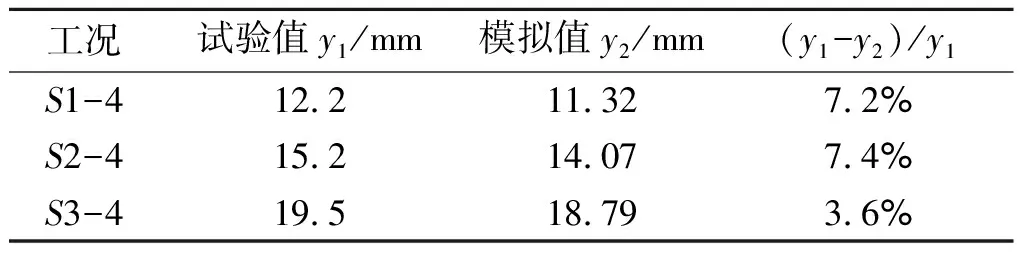
表 7 残余变形数值解与试验解比较Table 7 Comparison of residual deformation

图 4 工况S1-4迎爆面残余变形图Fig. 4 Residual deformation diagram of S1-4

2.2 加速度对比

为了进一步验证数值模拟方法的准确性和有效性，对试验工况S1-1中三个测点的加速度信号进行滤波降噪处理，获取真实反应的试验结果并与模拟结果进行对比分析。如图7所示，测点距试件中心位置越近，加速度越大，测点A1加速度最大值的试验结果为19 803 m/s2，模拟结果为18 337 m/s2，误差7.4%；测点A2加速度最大值的试验结果为15 228 m/s2，模拟结果为14 534 m/s2，误差4.6%；测点A3加速度最大值的试验结果为10 669 m/s2，模拟结果为9836 m/s2，误差7.8%；误差均在10%以内，模拟结果具有一定有效性。试验的采样频率为128 kHz，于是在模拟结果中每7.8 μs导出一个数据点，绘制A1测点100 ms内加速度时程曲线，如图8所示，试验结果与模拟结果基本吻合，说明数值模拟方法可以有效地反应爆炸载荷下钢管混凝土构件的动力响应。

图 5 工况S2-4迎爆面残余变形图Fig. 5 Residual deformation diagram of S2-4

图 6 工况S3-4迎爆面残余变形图Fig. 6 Residual deformation diagram of S3-4

图 7 工况S1-1加速度最大值对比Fig. 7 Comparison of maximum acceleration

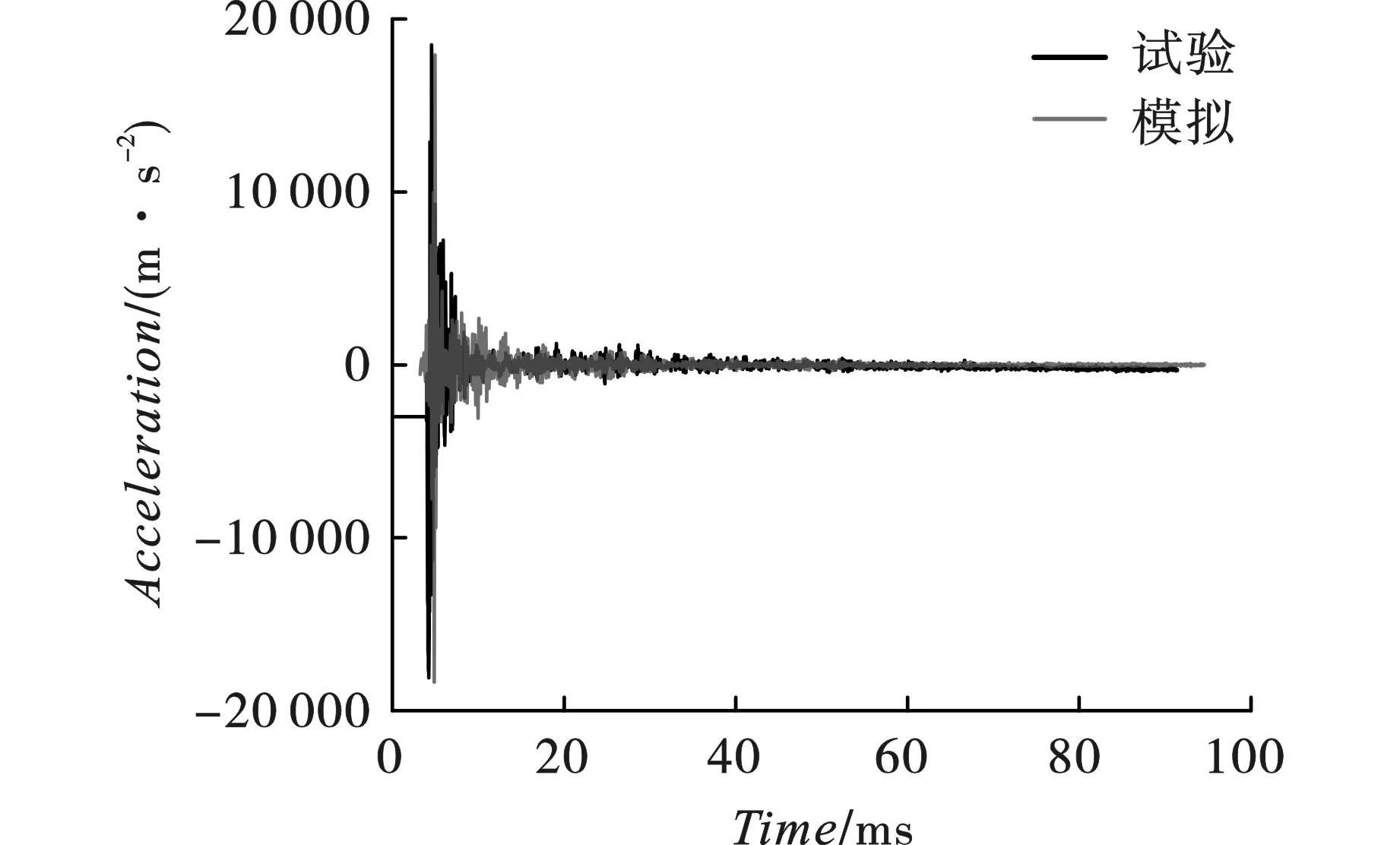
图 8 A1位置试验与模拟加速度时程曲线对比Fig. 8 Comparison of acceleration time history curves

3 模拟分析

下面通过上文介绍的数值方法对爆炸荷载作用下的钢管混凝土结构进行模拟研究，分析结构破坏机理以及混凝土强度和钢管厚度等参数对结构抗爆性能的影响，模拟工况如表8所示。

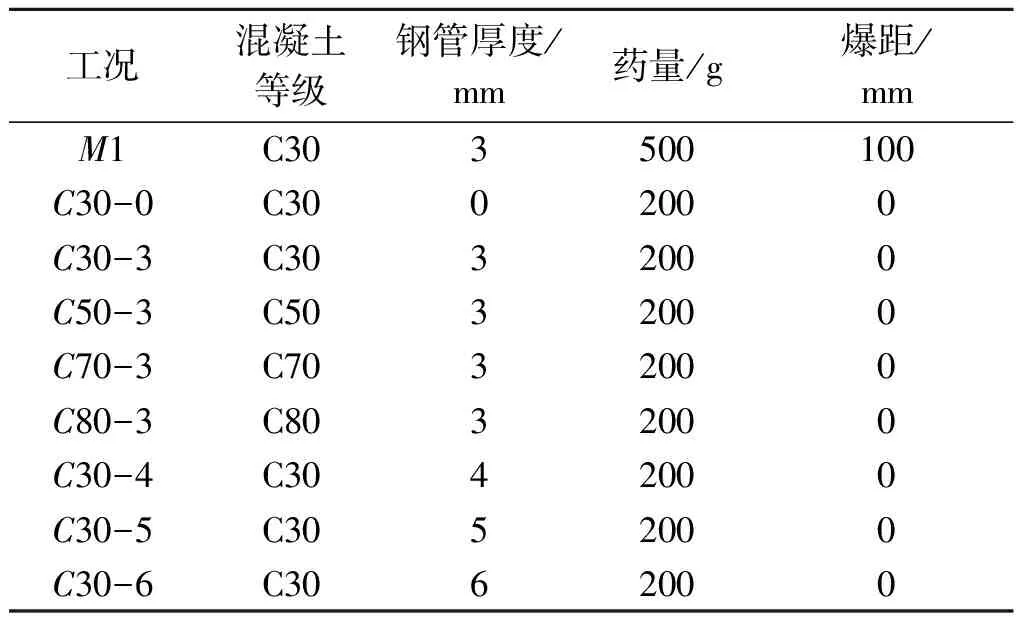
表 8 模拟工况Table 8 Simulated conditions

3.1 结构破坏过程分析

为了分析钢管混凝土在爆炸载荷作用下破坏机理，建立了500 g TNT在结构中心表面上方10 cm处爆炸的数值模型(工况M1)，钢管失效应变为0.24，混凝土失效拉应变0.009、失效压应变0.08，截取不同时刻钢管与混凝土变形破坏情况如图9所示。

图 9 不同时刻构件应变云图Fig. 9 Strain nephogram at different time

当爆炸冲击波作用到构件表面后，迎爆面中心位置钢管产生变形，核心混凝土达到失效应变，被压碎破坏；随着冲击波的继续作用，钢管产生塑性变形，混凝土破坏范围变广，跨中侧面出现鼓包，跨中位移逐渐增大，结构整体发生弯曲变形；冲击波继续传递至背爆面，发生反射作用，背爆面混凝土受拉破坏，但因钢管的约束作用，破坏面积较小；随后冲击波扩散至试件两端，端部受到约束产生变形，随着跨中位移越大，端部混凝土被拉破坏。

3.2 结构抗爆性能影响因素分析

3.2.1 混凝土强度的影响

为了研究爆炸荷载下内部混凝土强度对钢管混凝土构件抗爆性能的影响，模拟分析了4 种不同混凝土强度等级的构件模型在200 g TNT药量的爆炸荷载下的动态响应(工况如表8所示)。截取5 ms时间内背爆面中心位置的位移时程曲线如图10所示，当结构受到爆炸冲击波作用后产生弯曲变形，跨中位移逐渐增大；到达最大值后，由于结构两端受约束，冲击波作用减小，不足以支撑更大的变形，整体结构回弹，跨中位移减小；随后结构处于一个振动状态，位移振幅越来越小，最终处于一个固定值(残余位移)。背爆面中点位移最大值分别为5.056 mm、4.930 mm、4.838 mm、4.790 mm，绘制点线图如图11所示，最大值时刻的结构整体位移云图如图12所示，随着混凝土强度的提高，位移最大值逐渐减小且减小幅度有变缓趋势；构件整体变形变小，其中C30与C50等级混凝土的对比尤为突出；结构的抗爆性能越强。

3.2.2 钢管的影响

为了解钢管对钢管混凝土构件抗爆性能的影响，在混凝土强度等级为C30，TNT药量为200 g的基础上分别对素混凝土(无钢管)、以及4种不同钢管壁厚的构件进行了爆炸模拟分析对比(工况如表8所示)，图13为工况C30-0与C30-3的核心混凝土破坏情况对比，在同等爆炸荷载条件下，素混凝土构件破坏严重，背爆面大面积受拉破坏；而钢管混凝土构件因为钢管保护与约束作用，内部混凝土破坏较少，构件的抗爆能力大大提升。

图 10 背爆面中点位移时程曲线Fig. 10 The displacement time history curve

对比分析不同钢管厚度的钢管混凝土构件在爆炸荷载作用下的动态响应，截取5 ms内背爆面中心点位移时程曲线如图14所示。钢管越厚，位移时程曲线的振幅明显减小，振动频率加快，结构的刚度更高，抗爆性能更强。最大位移分别为5.056 mm、4.198 mm、3.609 mm、3.166 mm，变化趋势如图15所示。

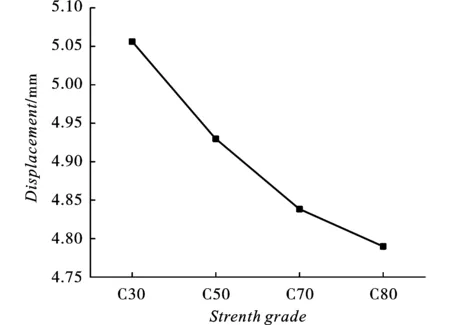
图 11 位移最大值对比Fig. 11 Comparison of maximum displacement

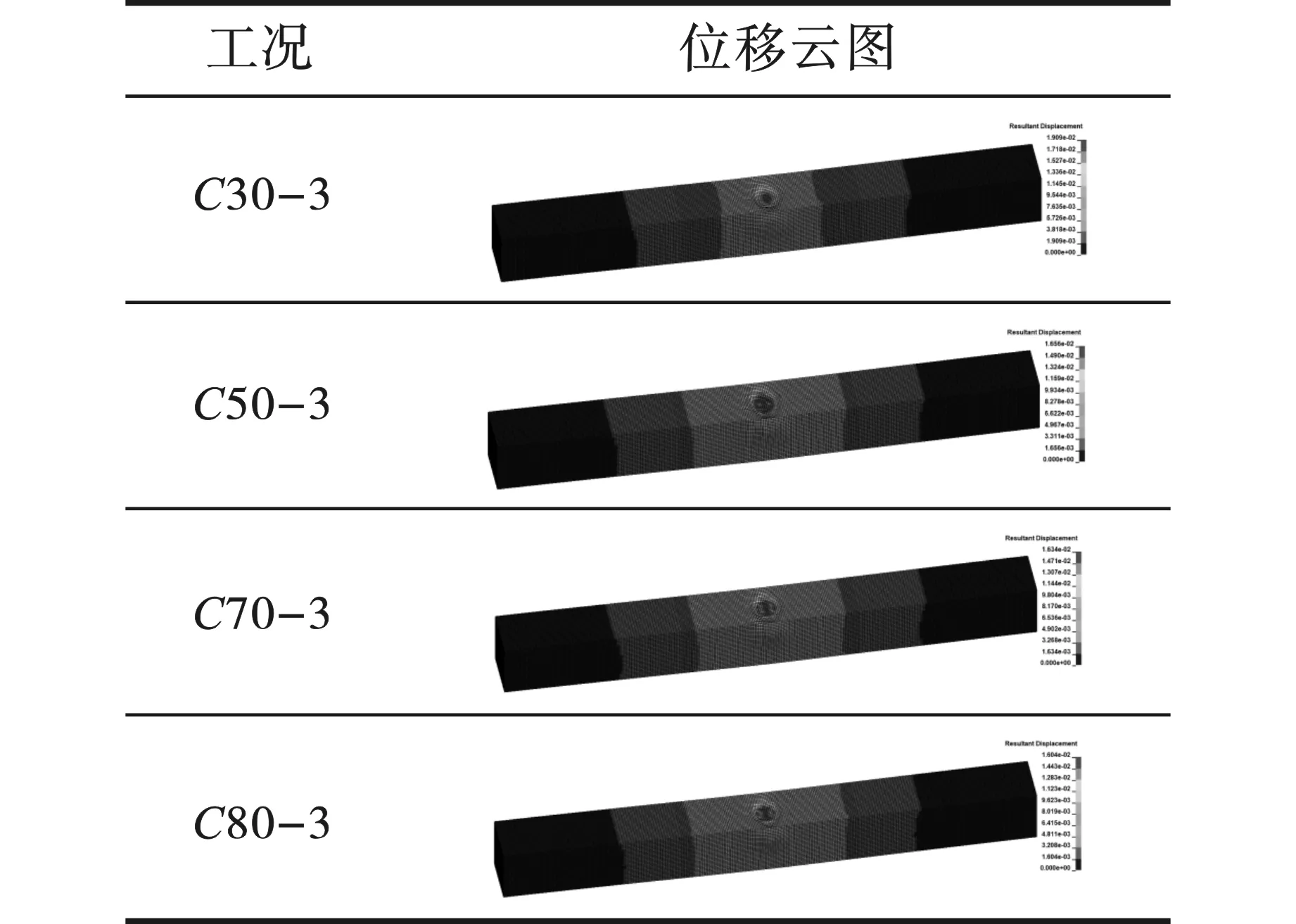
图 12 不同工况的位移云图Fig. 12 Displacement nephogram

图 13 混凝土破坏情况对比Fig.13 Comparison of concrete failure

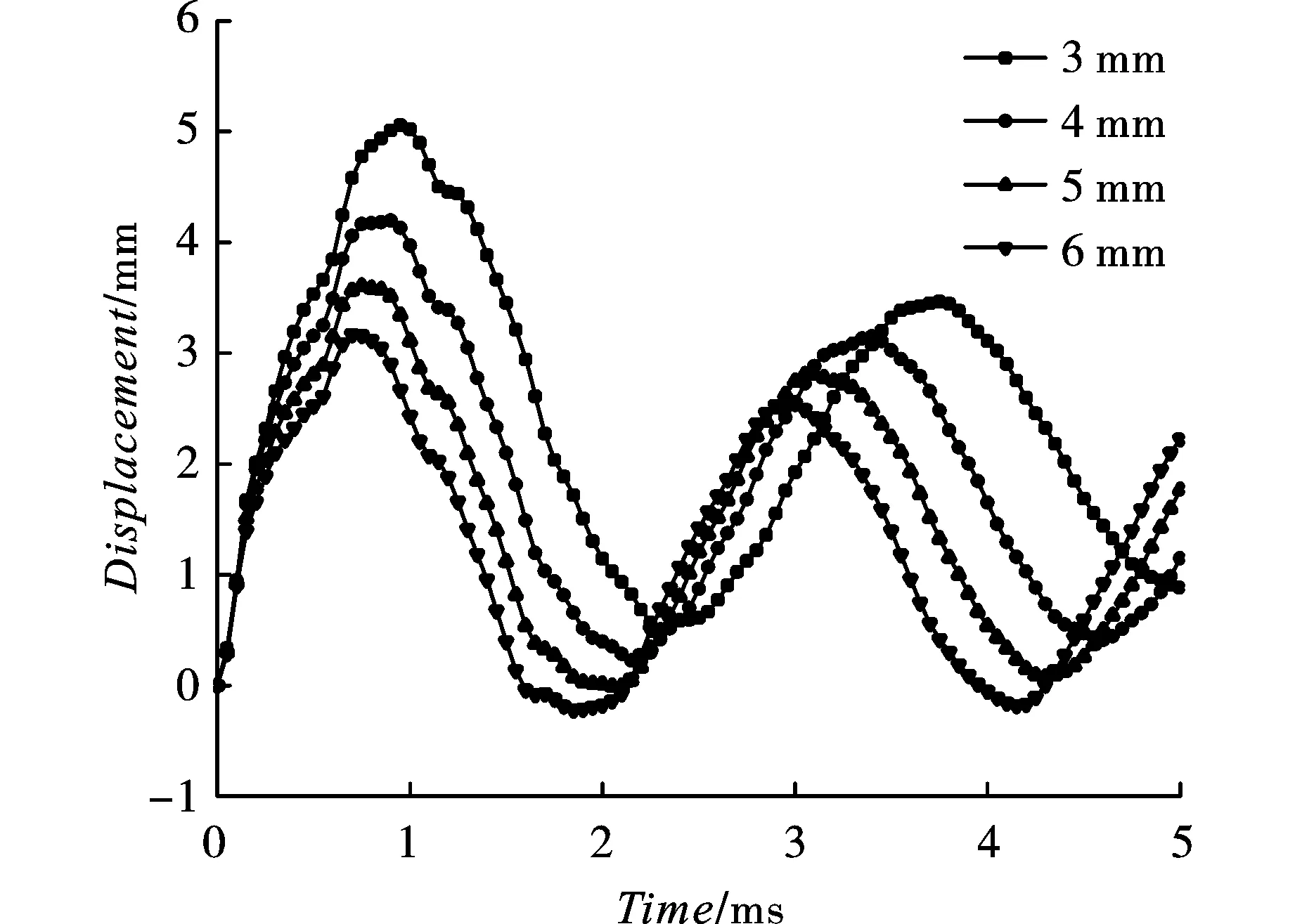
图 14 背爆面中点位移时程曲线Fig. 14 The displacement time history curve

图 15 位移最大值对比Fig. 15 Comparison of maximum displacement

最大值时刻不同钢管厚度下结构整体位移云图如图16所示。对比分析混凝土强度与钢管厚度两个参数对钢管混凝土结构抗爆性能的影响，发现，相同药量、爆距等条件下，钢管厚度的影响程度更大，增大钢管厚度比增大核心混凝土强度对钢管混凝土结构的抗爆性能的提高更为明显。

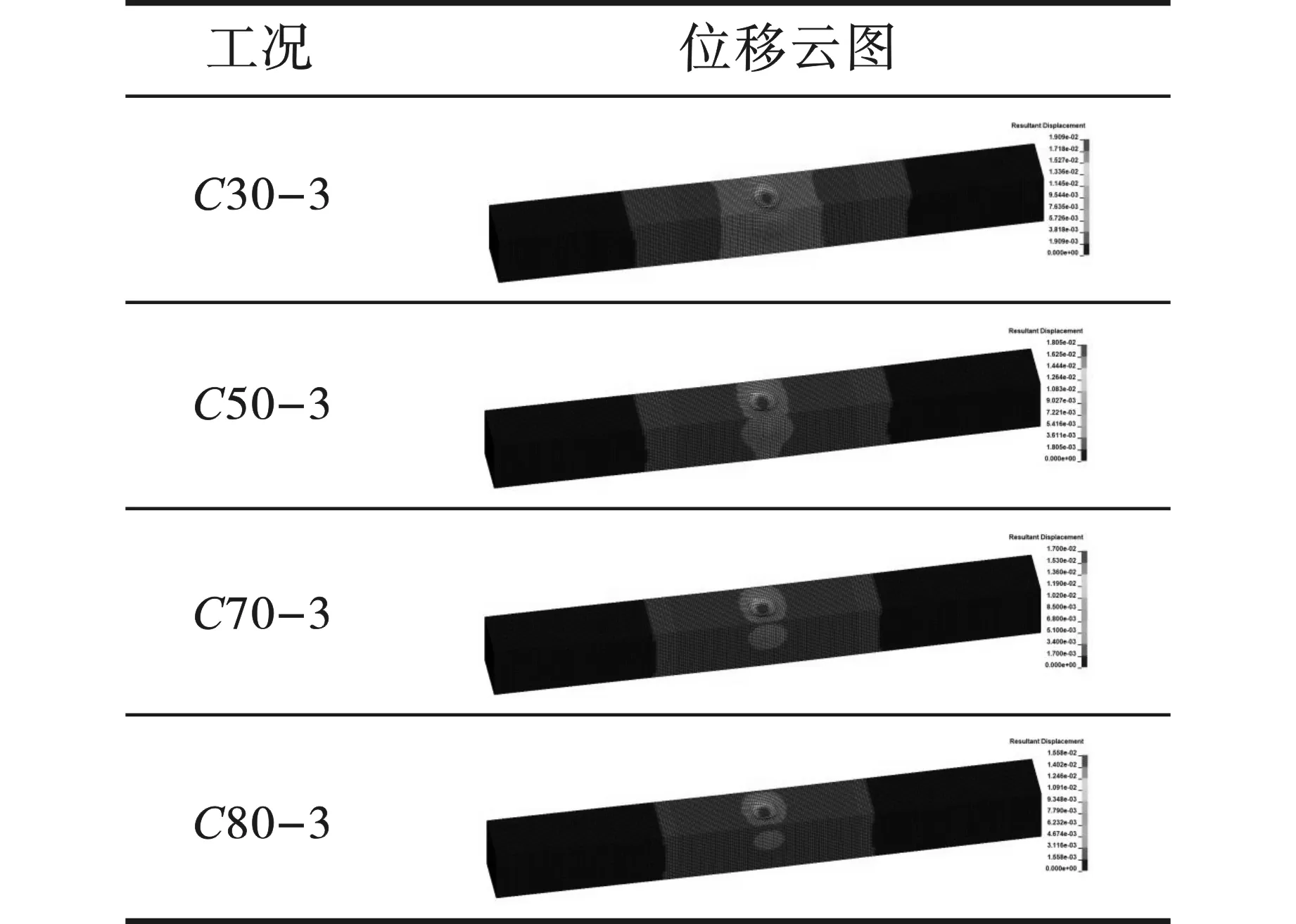
图 16 不同工况的位移云图Fig. 16 Displacement nephogram

4 结论

(1)本文数值模拟方法能够有效地模拟钢管混凝土结构在爆炸荷载作用下的动力响应。对比残余变形与加速度的模拟结果与试验结果，误差在10%以内。

(2)通过数值模拟系统分析了爆炸荷载作用下钢管混凝土动态响应过程。近距离爆炸下，钢管混凝土的破坏过程大致分为四个阶段：首先迎爆面中心位置钢管变形，混凝土被压碎，侧面出现鼓包；随后冲击波继续传递，构件发生弯曲变形，到达背爆面后发生反射，背爆面混凝土受拉破坏；然后冲击波到达构件端部，端部混凝土受拉破坏，跨中位移达到最大值；最后结构上下振动直至稳定，产生残余变形。

(3)钢管混凝土具有良好的抗爆性能；爆炸荷载作用下，提高核心混凝土强度和增大钢管厚度都能减小构件的位移变形，改善钢管混凝土结构的抗爆性能；增大钢管厚度，对结构抗爆性能的改善效果更明显。